例析立体几何中的球问题

李文东

(广东省中山市中山纪念中学 528454)

与几何体有关的球问题是立体几何的重点，也是高考考查的热点和难点，这类问题能充分考查学生的直观想象、数学抽象、逻辑推理核心素养，特别是对于多面体的外接球问题，各种文献和资料都有介绍，并且归纳和总结了各种不同的解题模型，这样不仅增加了学生的记忆负担，而且从高三的实际教学情况看，效果并不好，因此需要对这类问题探求通法求解.

1 多面体外接球问题

求解多面体外接球问题主要涉及到如下知识：

球心O与截面圆圆心O1的连线垂直于截面圆，设球的半径为R，截面圆O1的半径为r，球心O与圆心O1的距离OO1=d，如图1，则有R2=r2+d2,设AB为圆O1的一条弦，M为AB的中点，则OM⊥AB.

图1

这里包含以下三层含义：

(1)对于多面体的外接球，球心为过多面体各个面的外心且垂直该面的垂线的交点，特别地，正多面体的外接球的球心在高上；

(2)过球心作球内接多面体某个面的垂线，垂足为该面的外心；

对于外接圆半径的求法：当多面体的某个面为直角三角形时，其外接圆的圆心O1为斜边的中点；若是一般的三角形则可借助正弦定理确定外接圆的半径.

由余弦定理，得

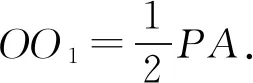
所以三棱锥P-ABC外接球的半径

所以三棱锥P-ABC外接球的表面积为4πR2=88π.

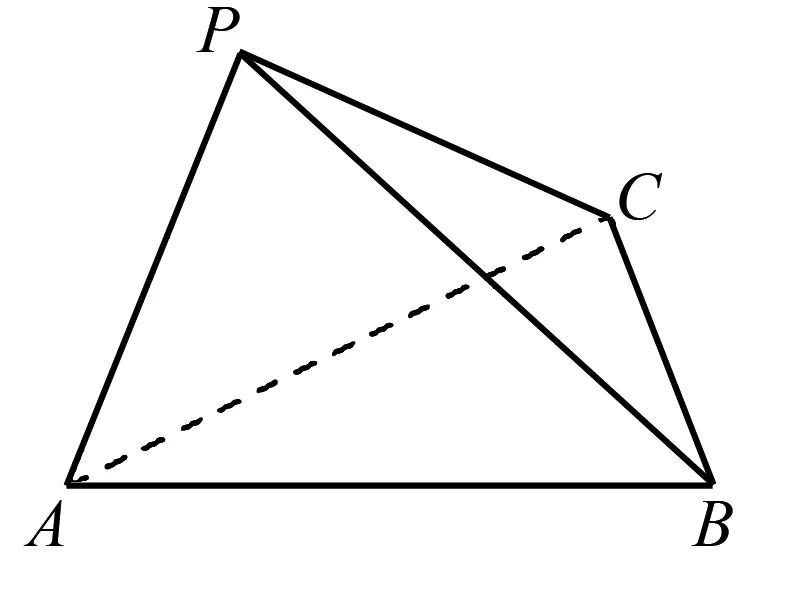
图2

解析根据题意，作出图形，如图3所示，

图3

因为△PAC是以AC为斜边的等腰直角三角形，

所以△PAC的外心在AC中点，设为O2，

设△ABC的外心为O1，BC中点为E，AO1=r1，

所以O1必在AE连线上.

因为两平面交线为AC，O1为平面ABC所在圆面中心，

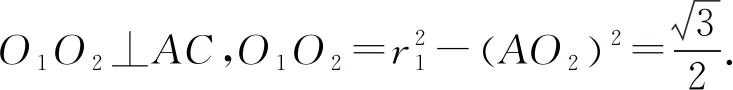
又因为二面角P-AC-B的大小为120°，PO2⊥AC，

所以∠PO2O1=120°,∠OO2O1=30°.

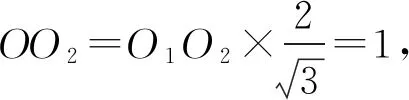
锥体P-ABC外接球半径

则三棱锥P-ABC的外接球表面积为S=4πR2=10π，故选B.

点评一般地，对于三棱锥P-ABC，二面角P-AC-B的大小为θ，则三棱锥P-ABC的外接球的半径R可由以下方法求出：

(1)分别求出△ABC和△PAC的外接圆半径r1,r2，其外接圆的圆心分别记为O1,O2；

(2)分别过点O1,O2作面ABC和面PAC的垂线，两垂线的交点O即为三棱锥P-ABC的外接球的球心；

(3)取AC的中点Q，则O1Q⊥AC，O2Q⊥AC，故∠O1QO2为二面角P-AC-B的平面角，即∠O1QO2=θ；

例3已知球O的半径为2，球心O在大小为60°的二面角α-l-β内，二面角α-l-β的两个半平面分别截球面得两个圆O1，O2，若两圆O1，O2的公共弦AB的长为2，E为AB的中点，四面体OAO1O2的体积为V，则下列结论中正确的有( ).

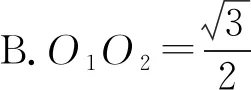
图4

因为二面角α-l-β的两个半平面分别截球面得两个圆O1，O2，O为球心，

所以OO1⊥α，OO2⊥β.

又O1E⊂平面α，O2E⊂平面β，

所以OO1⊥O1E，OO2⊥O2E.

故O，E，O1，O2四点共圆，故选项A正确；

因为E为弦AB的中点，故O1E⊥AB，O2E⊥AB.

故∠O1EO2即为二面角α-l-β的平面角.

所以∠O1EO2=60°.

设OO1=d1，OO2=d2，

在△OO1O2中，由余弦定理可得，

故选ACD.

2 与球相关的综合问题举例

例4如图5，在棱长为2的正方体ABCD-A1B1C1D1中，点E是棱DD1的中点，点F在正方体表面上运动．以下命题正确的是( ).

图5

A．侧面CDD1C1上不存在点F1，使得B1F1⊥CD1

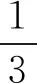
解析对于A选项，当F1是CD1的中点时，根据正方体的性质可知B1C=B1D1.

所以△B1CD1是等腰三角形.

所以B1F1⊥CD1，所以选项A错误.

对于C选项，设G,H分别是CC1,C1D1的中点.

由于GH∥CD1∥A1B，GH⊄平面A1BE，A1B⊂平面A1BE，所以GH∥平面A1BE.

由于B1G∥A1E,B1G⊄平面A1BE，A1E⊂平面A1BE，所以B1G∥平面A1BE.

由于GH∩B1G=G，

所以平面B1GH∥平面A1BE.

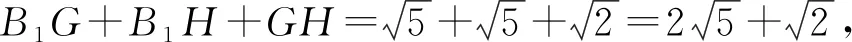
对于B选项,取CD的中点F，则EF∥A1B.

连接C1D交EF于点G，易知C1G∶GD=3∶1.

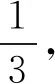
所以点F不在平面ABB1A1、平面ADD1A1、平面ABCD内.

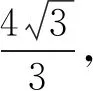
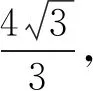
图6

B.当点E固定在线段DC某位置时，则D′在某圆上运动

C.当点E在线段DC上运动时，则D′在某球面上运动

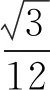
解析由等体积法，得

VA-BCF=VF-ABC

故选项A错误；

当固定点E时，由DA⊥DE，可知点D在以AE为直径的圆上运动，故选项B正确；

当点E在线段DC上运动时，AD′=1保持不变，即点D′的轨迹为以点A为球心，半径为1的球面的一部分，故选项C正确；

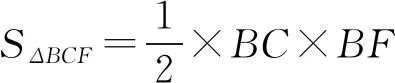
如图7，过点A作BF的垂线，垂足为点H，可得AH⊥平面BCF.

图7

因为点D′在以点A为球心，半径为1的球面上运动,则点D′到平面BCF距离的最小值为

点评本题的难点在于点E的轨迹的确定，对于D选项，类比圆的知识可知，球面上一点到球外一平面的最短距离为球心到该平面的距离减去球的半径.