浅谈正六边形的向量应用
2022-09-22杨伟达
杨伟达
(广东省广州市花都区第二中学 510800)
1 展示正六边形的向量模型,感受数学味道
例1 (新人教版高中数学必修第二册第一章例2)设O为正六边形ABCDEF的中心.(如图1)
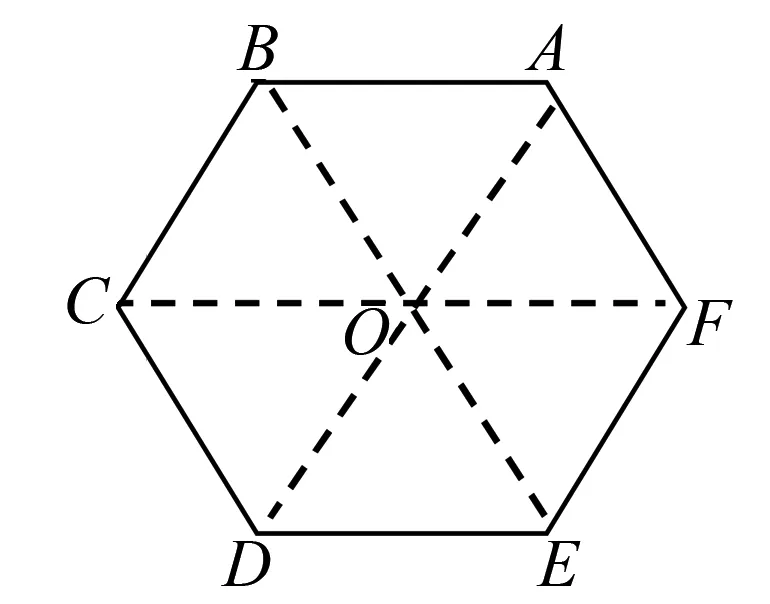
图1
(1)写出图中的共线向量;
分析本题关键是在正六边形ABCDEF中找出平行四边形.而ABCO的向量数式:借用向量表示对边平行且相等,它起到简洁、优美的效果,同时也代表一个简单图形.
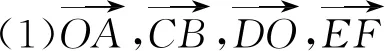
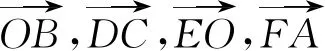
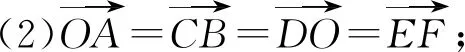

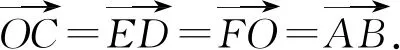
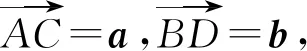
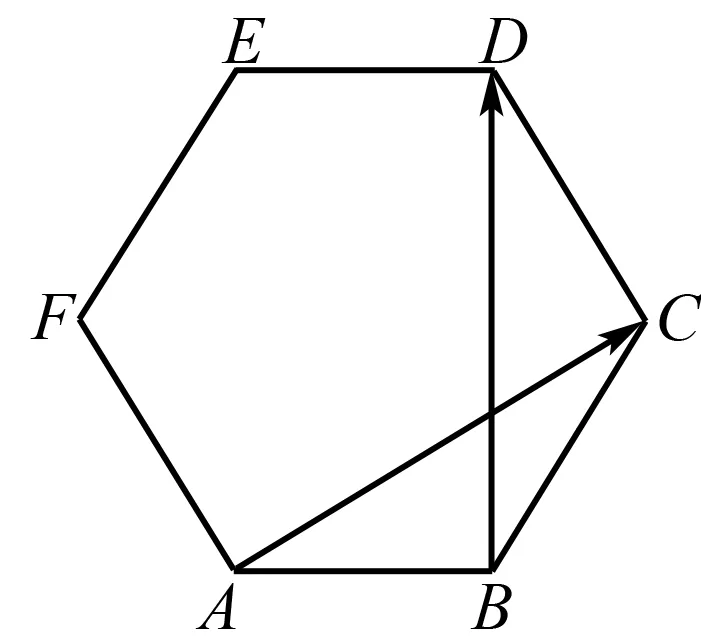
图2
分析本题考查了不共起点的向量基底.借用前面例题结果,利用向量的平行四边形法则和三角形法则即可.
方法1选用不同的基底,列方程组即可表示其它向量;
方法2特殊图形,可建立坐标系,用坐标法;
方法3转化为有交点的基向量,利用三角形法则即可.
解法1由图3可知,四边形ABCO,BCDO分别为菱形,其中AC,OB,BD,OC分别为对角线.
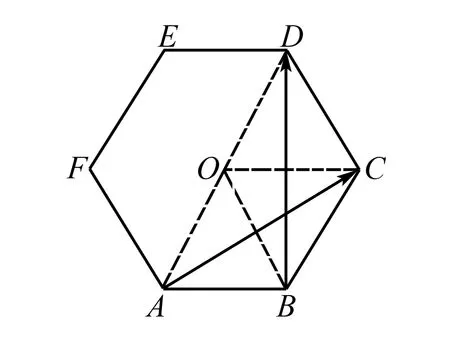
图3
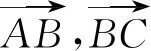
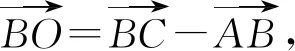
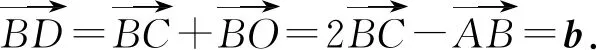
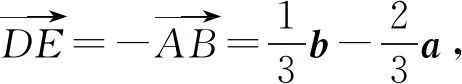
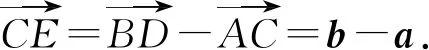
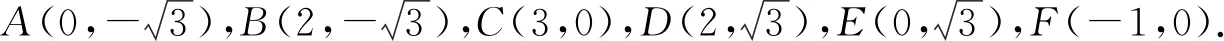

图4
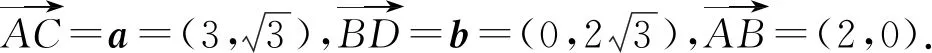
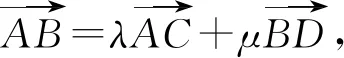

以下同解法1.

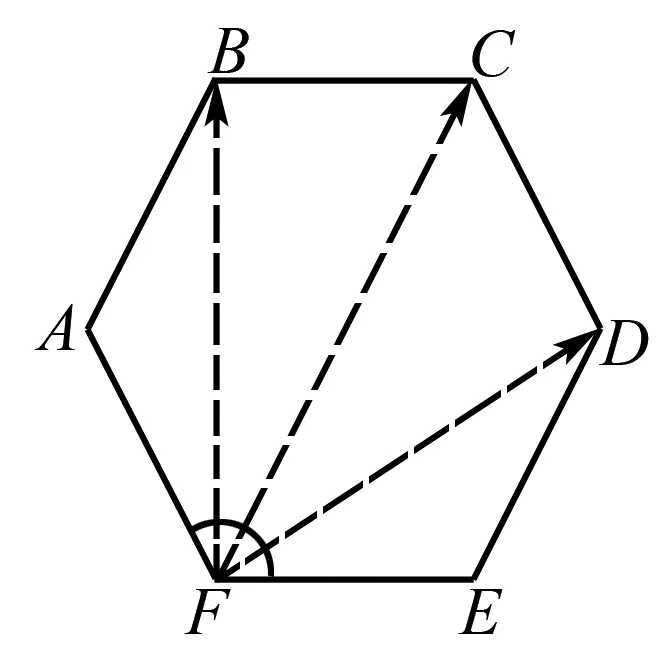
图5
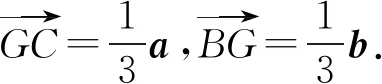

以下同解法1.
2 紧扣正六边形的向量内涵,突显核心素养
2.1 正六边形藴含的基本图形不简单
正六边形藴含的基本图形(1)有6个等腰三角形(如图6);(2)有8个等边三角形(如图6,9);(3)有6个直角三角形(如图7);(4)有6个菱形(如图8);(5)有3个矩形(如图10);(6)有6个等腰梯形(如图11);(7)正六边形的每一个角都蕴含着4个30°角;(8)正六边形的面积是6个等边三角形的面积之和.

图6 图7 图8

图9 图10 图11
2.2 向量工具不简单
向量工具神通广大,它作为解决长度、距离、角度、平行、垂直等问题的重要工具,有较好的融合度,与其他知识结合的试题累见不鲜.具体如下:
(1)利用其形的特点,通过向量运算的几何意义转化为平面几何的有关知识进行运算.形如:利用向量的数式表示直线、三角形、平行四边形、梯形、圆等.
(2)利用其数的特点,通过建立坐标系,将向量的有关问题转化为代数中的有关问题解决.形如:向量在坐标系中推导出距离、角度、平行、垂直等公式,同时推导出三角形的正余弦定理、勾股定理、射影定理等.
3 链接正六边形的高考试题,提升应用能力

A.(-2,6) B.(-6,2)
C.(-2,4) D.(-4,6)
分析本题考查了以正六边形为背景的向量数量积运用.(1)关键在于动点P所在位置.结合数量积的射影公式及正六边形的特点,确定数量积分别取得最大值、最小值时点P所在位置即可;(2)坐标法略.


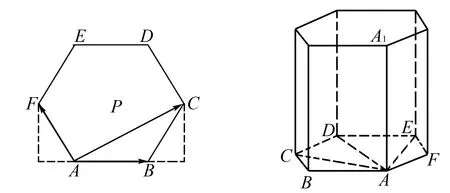
图12 图13


例4(2018年上海)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱,如图13,若阳马以该正六棱柱的顶点为顶点,以AA1为底面矩形的一边,则这样的阳马的个数是( ).
A.4 B.8 C.12 D.16
解析如图13,以AA1为底面矩形的另一边分别是AB,AC,AD,AE,AF,依题可知,在正六边形ABCDEF内分别找以AB为直角边的矩形、以AC为直角边的矩形、AE为直角边的矩形、AF为直角边的矩形,不难发现,AD为直角边的矩形是不能找到.所以下底面的阳马数是8,同理,上底面的阳马数也一样,所以阳马总数为16.故选D.
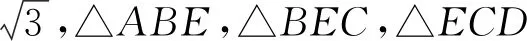

图14
A.18 B.24 C.36 D.48


图15

4 加强模型变式教学,追寻有效、高效
“高考题常考常新”,每一年的高考题、模拟题都会有不一样的新面孔.如何把新面孔落实到课堂教学活动中?当前有一种被称为有效课堂教学,那就是在某一模型的基础上,变更条件、编写变式题组,然后进行题组化训练.其目的是让学生熟悉考试题型,在短时间内记住题型的解题方法,对提高学生数学能力是很有帮助的.
4.1 变更题设条件(包括数学文化背景),结论不变


图16
4.2 变更题设结论,其它条件(包括数学文化背景)不变

图17 图18
5 一点感悟
新教材中的例、习题是专家们精心挑选的,蕴含着丰富的数学思想和方法.对这些具有代表性的正六边形范例,充分挖掘正六边形潜在功能,通过一题多解、多题一解、一题多变、推广探究等,把知识、素养落到实处,引领学生探究,真正达到有效、高效.
