初高中数学竞赛中“整数解问题”的探索研究

孙 宇

(江苏省宜兴市硕博教育中心 214200)

1 整数解问题的一般方法

在初高中的数学竞赛和高中自主招生考试中，整数解问题是最热门的题型之一.整数解问题一般方法分为三种：

1.1 分式类型的整数解问题

对于分式类型的整数解问题可以利用分离常数法进行求解.

通过分离常数进行变形：

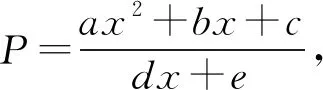
可以通过平方差公式进行分离常数的变形：

从而转化为上述的解答方法.

1.2 一元二次方程的整数解问题

对于一元二次方程的整数解问题可以设出根的判别式，利用平方差公式进行因式分解.

例如，对于关于x的一元二次方程ax2+mx+c=0有整数解(a,c均为整数)，m为整数，且m是参数.

则Δ=m2-4ac必定是一个完全平方数.

从而设Δ=m2-4ac=n2,(n为自然数)

则m2-n2=4ac.

所以(m+n)(m-n)=4ac.

由于a,c,m都是整数，n是自然数，所以(m+n)，(m-n)必然是4ac的整因子且其奇偶性相同.从而可以求得m,n的值，最后代入求根公式求解x的值.

1.3形如kmn+pm+qn=r(m,n为参数且m,n是整数，k,p,q,r为常数)的二元二次方程的整数解问题

对于形如kmn+pm+qn=r(m,n为参数且m,n是整数，k,p,q,r为常数)的二元二次方程的整数解问题可以直接进行因式分解.对于这一类的因式分解，有两种方法进行变形.

第一种：

第二种：

转化为第二种进行求解.

如果k,p,q,r为分数，则可以先转化为整系数代数式进行求解.

1.4 形如pm2+km=qn2+rn+t(k,p,q,r,t为常数，m,n为参数且m,n为整数)的二元二次方程

对于形如pm2+km=qn2+rn+t(k,p,q,r,t为常数，m,n为参数且m,n为整数)的二元二次方程，首先进行配方，得到关于m,n的平方项.

然后利用平方差公式将m,n的代数式进行因式分解，转化为上述的的情况.

2 典型例题剖析

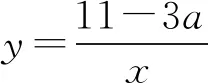
分析该题来自于2007年全国初中数学联赛二试的压轴题，是一道很典型的整数解问题.将两个方程联立，得到一个关于x的一元三次方程，所以第一个关键点在于找到三次方程的一个有理根，然后再将该三次方程进行因式分解，得到关于x的一元二次方程，把题目转化为一元二次方程的整数解问题.最后就可以利用上述平方差的方法进行因式分解，求得最终结果.

解析联立方程

即2x3+(2a+23)x2+(10-7a)x+3a-11

=0.

①

将①式变形可得

(2x2-7x+3)a+2x3+23x2+10x-11=0.

则可将①式分解因式，得

(2x-1)[x2+(a+12)x+11-3a]=0.

②

如果两个函数图象有公共整点，则方程①必有整数根，从而方程②中关于x的一元二次方程x2+(a+12)x+11-3a=0③必有整数根.所以方程③的判别式Δ是一个完全平方数.

从而设Δ=(a+12)2-4(11-3a)=a2+36a+100=(a+18)2-224=n2(其中n为非负整数)，则(a+18)2-n2=224.

即(a+18+n)(a+18-n)=224.

显然a+18+n与a+18-n的奇偶性相同，且a+18+n≥18，且224=112×2=56×4=28×8，

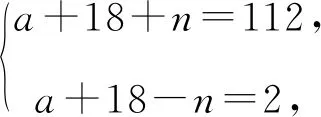
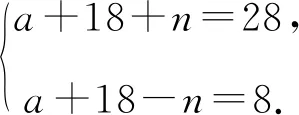
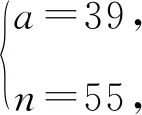
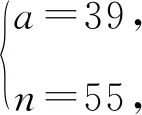
当a=39时，方程③为x2+51x-106=0，其根为2或-53，则可得两个函数图象的公共整点为(2,-53)或(-53,2).

当a=12时，方程③为x2+24x-25=0，其根为1或-25，则可得两个函数图象的公共整点为(1,-25)或(-25,1).

例2已知二次函数y=x2+bx-c的图象经过两点P(1,a)，Q(2,10a).设二次函数y=x2+bx-c的图象与x轴的交点为A,B，与y轴的交点为C.如果关于x的方程x2+bx-c=0的两个根都是整数，求△ABC的面积.

分析该题来自于2010年全国初中数学联赛二试压轴题.首先通过消元将参数b,c均用a的代数式表示.这是很关键的一步，为第二问做好铺垫！该问的最关键点在于利用根与系数的关系表示方程的两个根m,n，再将参数a消去，得到关于m,n的二次方程，然后再利用二元二次方程的因式分解方法进行求解.

解析由于P(1,a)，Q(2,10a)两点在二次函数图象上，代入解析式可得

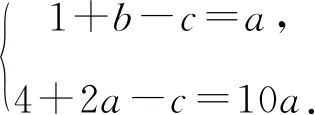
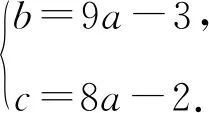
设m,n是方程x2+bx-c=0的两个整数根，且m≤n，由根与系数的关系可得

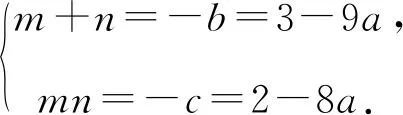
消去参数a可得

9mn-8m-8n=-6.

④

则9m·9n-8×9m-8×9n=-54.

由于m,n是整数，对等式左边进行因式分解可得(9m-8)(9n-8)=10.

而10=1×10=2×5=(-1)×(-10)

=(-2)×(-5),

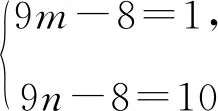
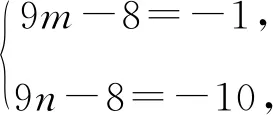
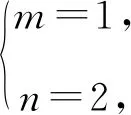
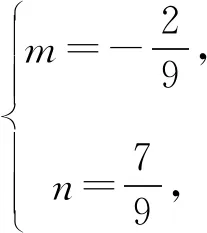
则b=-(m+n)=-3，

c=-mn=-2.

所以二次函数解析式为y=x2-3x+2.

则A(1,0)，B(2,0)，C(0,2).

所以S△ABC=1.

注对于④式进行因式分解，如果不太熟练的话，可以进行如下变形：

对等式左边进行因式分解可得

由于m,n是整数，所以(9m-8)(9n-8)=10.

例3二次函数f(x)=x2+x+11图象上是否存在这样的点，其横坐标是正整数，纵坐标是一个平方数？如果存在，求出这样的点的坐标；如果不存在，请说明理由.

分析该题来自于2011年高中数学联赛湖北省预赛，难点在于第二问的整数解问题的转化：设出点P坐标(m,n2)后，得到关于m,n的方程，此时需要注意，由于方程中含有m的一次项而没有n的一次项，所以首先将关于m的代数式进行配方，得到关于m的平方项，然后再利用平方差公式进行因式分解，就可以求出最后的结果.

解析设点P(m,n2)是符合条件的点，其中m是正整数，n为自然数.

则m2+m+11=n2.

所以4n2-(2m+1)2=43.

则(2n+2m+1)(2n-2m-1)=43.

由于43是质数，且2n+2m+1>2n-2m-1，2n+2m+1>0,

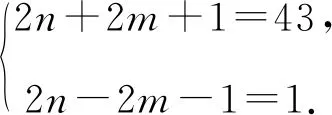
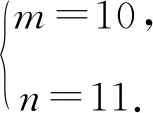
所以函数y=f(x)的图象上存在符合条件的点，其坐标为(10,121).

在整个中学数学竞赛中，整数解问题层出不穷，在各大高校的自主招生、强基计划中也屡见不鲜.因此理解并学会利用“因式分解”这一最基本也是最重要的方法是必须的.在解答这类题目时，我们需要注重数学思想方法的激活与运用，不能过于关注“述”，而轻视“法”、忽略“道”,更加要关注题设的条件和解答的方法，更需要通过回顾与反思，来理解题目中的本质结构.因此，我们需要更加用心钻研，总结经验和方法，这样才能一通而百通.