平面向量等值线定理及其应用

何少杰

(甘肃省清水县第六中学 741400)

平面向量基本定理是向量坐标表示,以及向量法求解几何问题的理论基础,由其引出了几个系数等值线定理,笔者在高三复习教学时注意到,在解决向量线性表示后的系数问题时,等和线与等差线能让学生从形的角度去分析问题,解法直观,过程简洁流畅,可以拓展思维,加深学生对平面向量基本定理的理解,应用最为广泛,是解决此类问题的通法.文[1]给出了定理的证明过程,下面整理性质并进行应用举例,供考生参考.

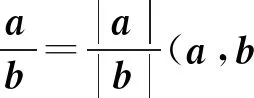
1 等和线

1.1 等和线定理

1.2 等和线性质

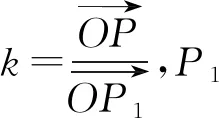
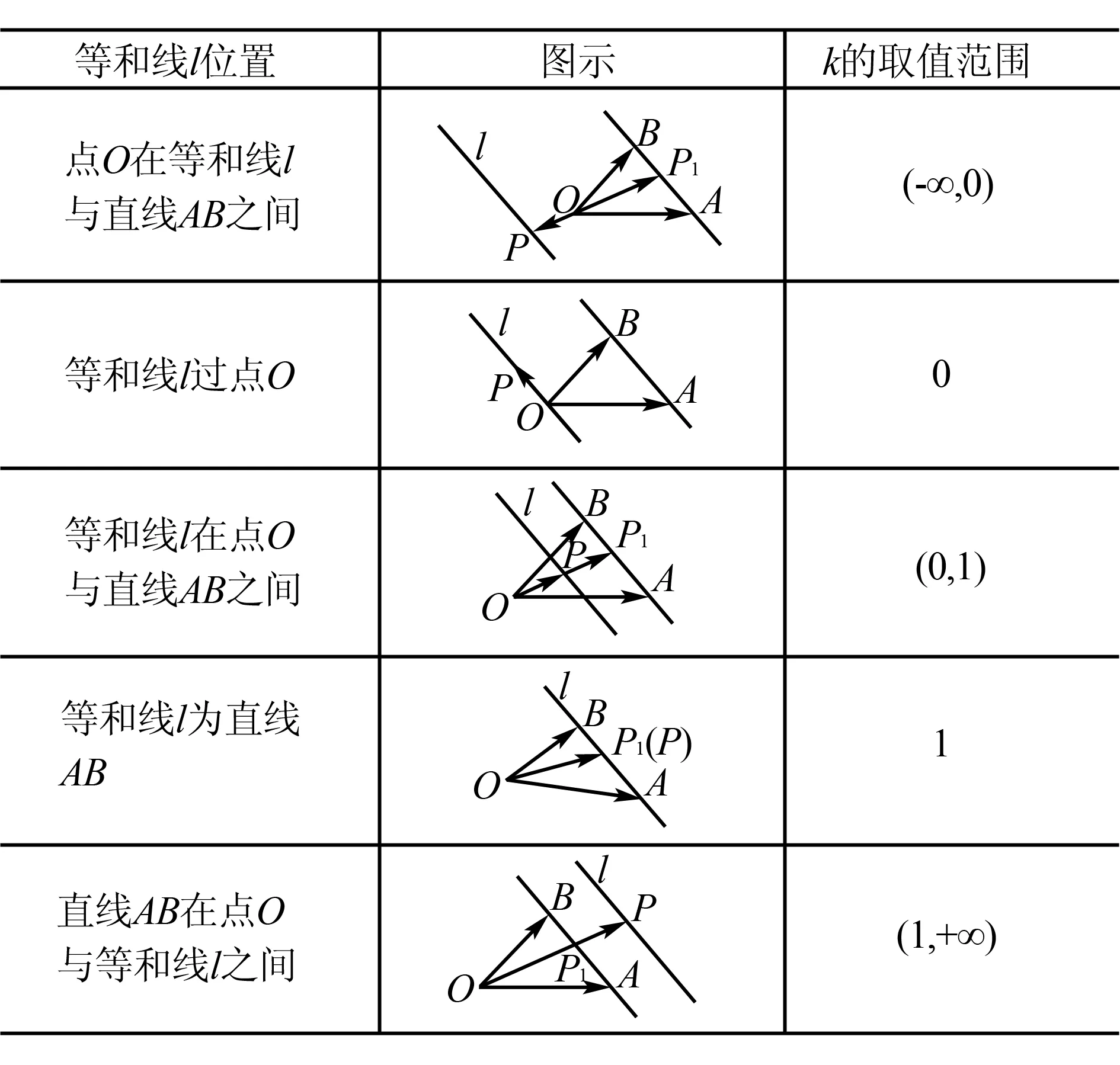
表1 等和线性质

1.3 等和线应用举例

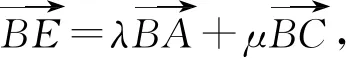
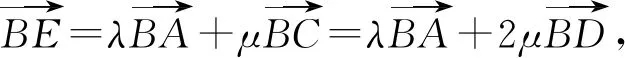
所以λ2+μ=(1-2μ)2+μ.

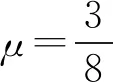
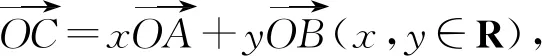
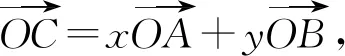
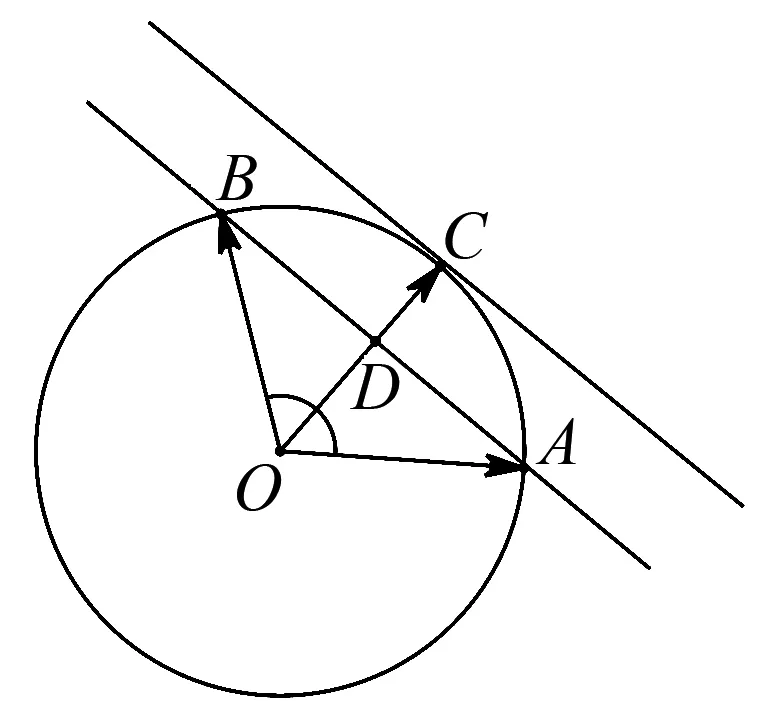
图1

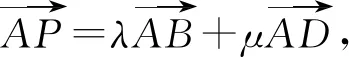
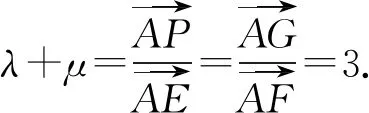
图2

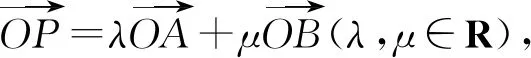
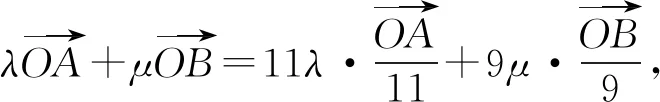
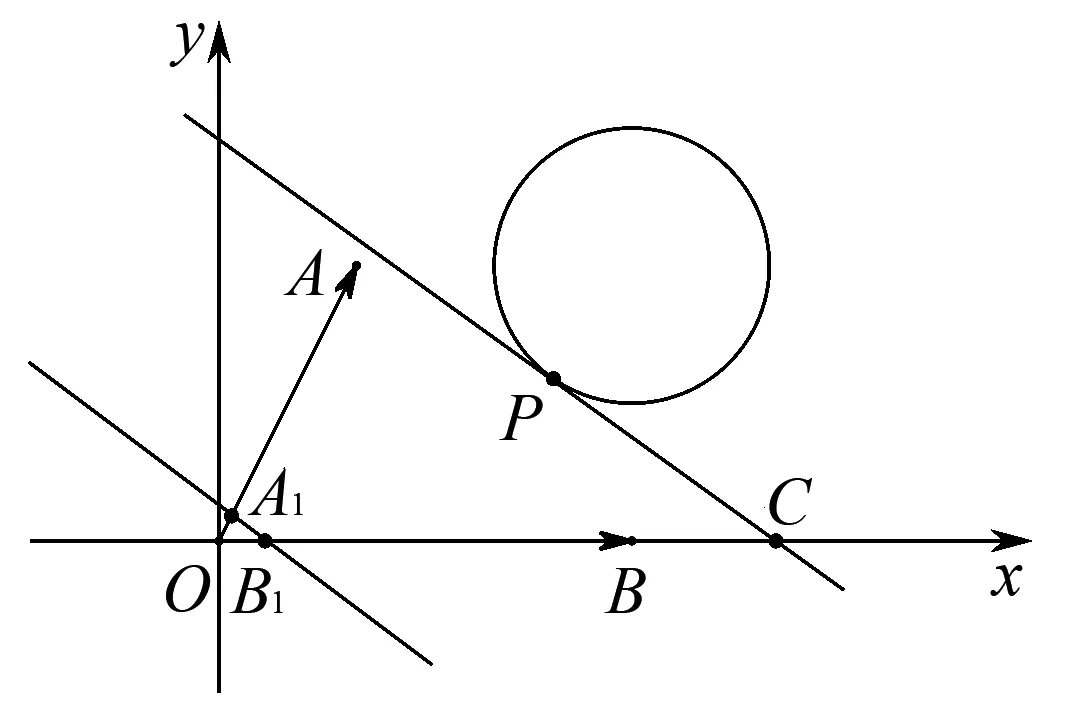
图3

可求得切线PC方程为3x+4y-12=0.

所以|OC|=4.

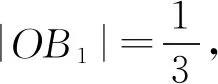
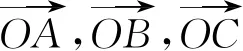
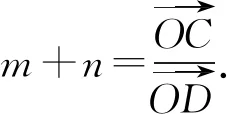
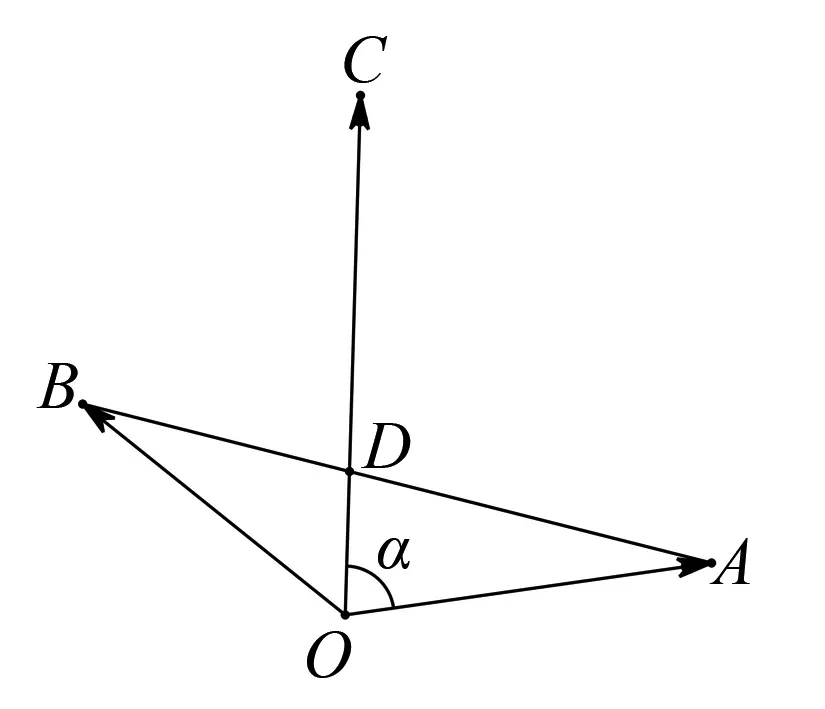
图4

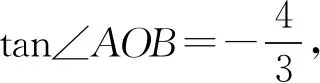
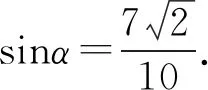
又S△AOB=S△AOD+S△BOD,

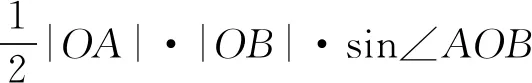
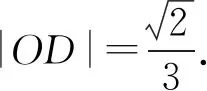
2 等差线

2.1 等差线定理

2.2 等差线性质

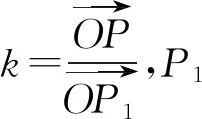
表2 等差线性质

2.3 等差线应用举例

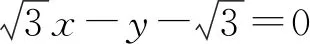
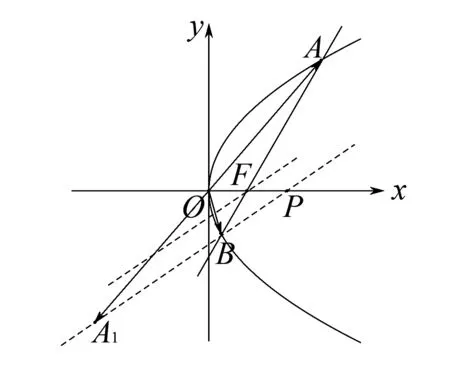
图5

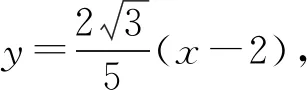
令y=0得P(2,0).

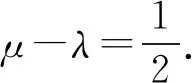
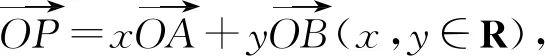
解析如图6,由等和线定理,平行移动等和线AB至MN,可得x,y需满足1≤x+y≤2.

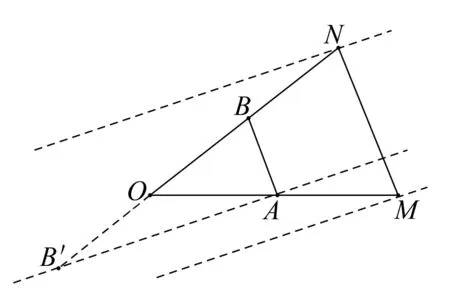
图6

由等差线定理,平行移动等差线AB′,当等差线过点M时,(x-y)max=2,当等差线过点N时,(x-y)min=-2,得x,y还需满足-2≤x-y≤2.

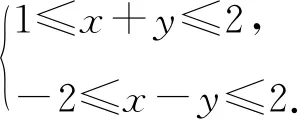
3 对等值线的解读

定理中系数取定值的等式分别为x+y=k,x-y=k,与平面直角坐标系中的直线方程形式完全一致,而且系数取定值时点P轨迹也是直线,难道是巧合吗？

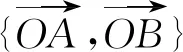
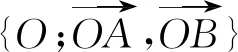
基于以上认识,类比平面直角坐标系中的相关概念,在对应的平面仿射坐标系中,对等值线中的k可以赋予一定的几何意义.等和线方程x+y=k变形为y=-x+k,则k对应的就是“纵截距”;等差线方程x-y=k变形为y=x-k,则k对应的就是“纵截距的相反数”.至此,我们从另一角度更深刻地认识了平面向量基本定理系数等值线,也可以理解并记忆不同图形所对应的k的取值情形.