μ2算法的积分攻击和不可能差分攻击

胡 斌 张贵显

(战略支援部队信息工程大学 郑州 450001)

1 引言

积分攻击是由Knudsen等人[1]在FSE 2002上提出的一种密码分析方法。该攻击方法是继差分分析和线性分析之后，密码学界公认的最有效的分析方法之一。2015年欧密会上，Todo[2]提出了推广的积分性质--可分性(division property)，极大地改进了积分区分器的搜索结果。2015年美密会上，Todo[3]将可分性应用到MISTY1密码算法上，攻破了全轮的MISTY1算法。然而，对于基于非S盒构造的分组密码算法，基于字可分性搜索得到的积分区分器与通过实验穷举获得的积分区分器之间仍有差距，这说明字可分性仍然不够精确。2016年FSE会议上，Todo等人[4]提出二子集比特可分性和三子集比特可分性，可以找到更精确的积分区分器。但是当密码算法的分组规模n比较大时，刻画中间状态可分性的时间复杂度和存储复杂度会变得十分大，这导致比特可分性无法应用到分组规模较大的分组密码算法上。2016年亚密会上，Xiang等人[5]将二子集可分性的刻画问题转化为混合整数线性规划问题(Mixed Integral Linear Programming,MILP)，进而用MILP求解器进行求解，改进了分组密码积分区分器搜索结果。2019年CT-RSA会议上，Hu等人[6]提出了一种简化的三子集可分性，并将他们转化为SMT问题进行求解，改进了已有的积分区分器搜索结果。2019年亚密会上，Wang等人[7]通过提出“剪枝技术”来约简冗余向量，有效解决了基于比特的三子集可分性的自动化刻画问题，对基于比特的可分性的自动化刻画问题进行了理论完善。2020年亚密会上，Hu等人[8]从代数角度重新描述了可分性，进一步诠释了可分性的含义。

差分分析[9]由Biham和Shamir在1990年第1次提出。该攻击方法是攻击迭代型分组密码最有效的方法之一，也是衡量分组密码安全性的重要指标。评估一个密码算法抵抗差分密码分析的能力主要有两个方面：一是获取差分活跃S盒数目的下界；二是搜索最大概率的差分特征。Mouha等人[10]和Wu等人[11]将计算差分活跃S盒的最小数目问题转化为MILP问题。2014年亚密会上，Sun等人[12]改进了基于MILP的评估分组密码抵抗差分分析能力的算法，并提出一个启发式算法去寻找差分特征。随后，Sun等人[13]构造了带概率的MILP传播模型来寻找最优的差分特征。然而，随着轮数的增加，MILP模型包含的不等式的数目急剧增加，导致模型的求解效率低下，以致到达一定轮数之后模型常常无法求解。为了提升搜索效率，2017年SecITC会议上，Sasaki等人[14]基于SageMath生成的不等式，提出了寻找刻画S盒可分链和差分特征的最少不等式的方法。2019年FSE会议上，Zhou等人[15]结合“分而治之”的思想改进了部分分组密码抵抗差分/线性攻击能力的评估结果。2020年FSE会议上，Boura等人[16]将SageMath生成的不等式进行相加获取更多候选不等式，然后再利用Sasaki等人的方法寻找最少的不等式，从而进一步约简了不等式。目前，基于MILP评估分组密码抵抗差分攻击能力已经逐渐发展成为一种成熟的方法。

不可能差分分析由文献[17]和文献[18]分别独立提出[17,18]，是差分分析的一个重要的变体之一。与差分分析利用高概率差分特征恢复密钥相反，它利用的是概率为0的差分特征，其基本思想是排除那些使概率为0的差分特征成立的候选密钥。对于不可能差分，当用正确密钥脱密密文对时，一定不会得到符合该路径的差分；当用错误密钥脱密密文对时，得到的差分会随机分布，如果某个密钥满足该路径的差分，那么该候选密钥一定为错误密钥；那么筛去所有的错误密钥猜测值，剩下的就是正确密钥。

µ2算法是由Yeoh等人[19]于2019年设计的一个分组长度为64 bit，密钥长度为80 bit的轻量级分组密码算法。该算法共15轮，采用TYPE-II广义Feistel结构，F函数采用重复4次的S-P结构，其中S层为4个并置4 bit S盒，P层采用比特拉线，S盒与PRESENT算法中的S盒一致。µ2算法与已有的密码算法相比有更高的吞吐率。设计者在设计文档中对µ2算法抵抗差分分析、线性分析的能力进行简要介绍。然而，µ2算法抵抗积分攻击和不可能差分分析的能力尚不清楚，因此本文对该算法进行了积分攻击和不可能差分分析，并对该算法抵抗差分分析的能力给出进一步的评估。

本文具体贡献如下：首先，为了评估µ2算法抵抗积分攻击的能力，本文利用基于比特的可分性结合MILP搜索工具对µ2算法的积分区分器进行搜索。为了提升搜索效率，本文结合Boura等人[16]的方法将描述S盒可分链的不等式的数目从11降到7，最终得到µ2算法的8轮和9轮积分区分器，并利用8轮积分区分器对9轮的µ2算法进行积分攻击，攻击的时间复杂度为 276次9轮加密，数据复杂度为 248，存储复杂度为 248。其次，为了评估µ2算法抵抗不可能差分攻击的能力，本文采用中间相遇法得到了9轮的截断不可能差分，为了进行更长轮数的密钥恢复攻击，在9轮不可能差分后面添加两轮，可以对11轮µ2算法进行攻击，攻击的时间复杂度为249次11轮加密，数据复杂度为 264个明文。最后，本文基于MILP对µ2算法抵抗差分攻击能力给出进一步的评估，并证明4轮µ2算法的差分特征的最大概率为 2-39，与设计报告指出的4轮差分特征的概率不超过2-36相比结果更为紧致。

本文的结构安排如下：第2节主要对µ2算法进行介绍；第3节给出µ2算法积分攻击的具体过程和复杂度计算；第4节给出µ2算法的不可能差分分析的具体过程和复杂度计算；第5节对µ2算法抵抗差分分析能力进一步评估，给出更紧致的安全界限；第6节总结全文。本文的程序均通过Python编程实现，在以下平台上进行：AMD R7-4800H CPU@2.9 GHz, 16 GB RAM；Python的运行环境为VS2019；MILP模型求解器为Gurobi9.0.2；本文所有的程序和实验结果被放置在以下网站：https://github.com/zgxxgz111/integral-attack-andimpossible-difference。

2 µ2算法介绍

2.1 µ 2算法的加密过程

2.2 µ 2算法的密钥扩展方案

2.3 µ 2算法的F函数

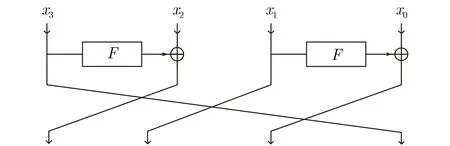
图1 µ 2算法结构图

3 对 µ2算法的积分攻击

目前来说，自动化搜索积分区分器的方法主要有两种：基于二子集比特可分性和基于三子集比特可分性。根据文献[7]的结果得知，与二子集比特可分性相比，三子集比特可分性虽然可能会搜索得到更多的平衡比特，但是积分区分器的轮数往往不会有所突破。同时利用三子集比特可分性搜索积分区分器的时间复杂度较高，搜索效率较低。由于本文主要立足于进行积分攻击同时考虑到搜索效率，所以我们利用二子集可分性搜索积分区分器。

图2 S-P结构图

图3 F函数图示

表1 S盒

3.1 比特可分性及其传播规则

S盒的MILP模型 利用规则1得到S盒的47个可分链，然后通过SageMath数学软件可以得到327个线性不等式来刻画S盒可分链，并利用文献[13]的贪婪算法来约简不等式组，最终得到11个不等式。为了减少描述S盒可分链的不等式的数目从而提升搜索效率，本文采用文献[16]中约简刻画S盒差分特征的不等式的方法。针对每一个可分链p=(x0,x1,x2,x3,y0,y1,y2,y3)，将SageMath生成的327个不等式中经过可分链p=(x0,x1,x2,x3,y0,y1,y2,y3)的不等式两两相加，然后对这些不等式进行检测，如果这些不等式能移除不同的可分链集合，那么保留这个不等式。通过这种方法，获得了1019个候选不等式。然后再利用Sasaki等人[14]的方法来寻找最小的不等式数目，最终得到7个不等式来刻画S盒的可分链。

3.2 搜索积分区分器

3.3 9轮µ 2算法的积分攻击

表2 积分区分器

4 对 µ2算法的不可能差分分析

4.1 µ 2算法的9轮不可能差分

定理1µ2算法存在形如(000α)↛(000α)的9轮截断不可能差分，其中0,α均 为16 bit向量且α/=0。

4.2 11轮µ 2算法的不可能差分分析

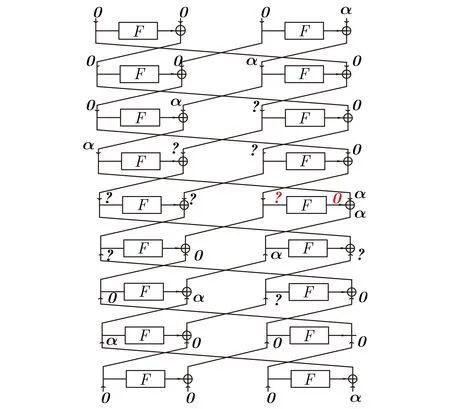
图4 µ 2算法的9轮不可能差分

5 对 µ2算法的抗差分分析能力的评估

在设计文档中，设计者对µ2算法抵抗差分分析的能力进行了评估，本节基于MILP对µ2算法抵抗差分分析的能力进一步评估。

5.1 针对基于比特设计的密码算法的评估框架

图5 µ 2算法的11轮不可能差分攻击

5.2 µ 2算法抵抗差分分析的能力评估

本文将上述方法应用到µ2算法，得到2轮µ2算法最优差分特征的概率为 2-12， 3轮µ2算法最优差分特征的概率为 2-24，这与设计报告的评估结果一致。然而本文搜索得到4轮µ2算法最优差分特征的概率为 2-39，与设计报告指出的4轮差分特征的概率不超过 2-36相比更为紧致。计算复杂度的限制使我们无法搜索更高轮数最优差分特征。然而µ2算法全轮共有15轮，我们相信有较大的安全空间抵抗差分密码分析。关于4轮µ2算法最优差分特征的结果如表3所示。

表3 4轮µ 2算法最优差分特征

6 结束语

本文首次对µ2算法抵抗积分攻击和不可能差分分析的能力进行评估，分别得到了µ2算法的8轮和9轮积分区分器和9轮不可能差分，从而进行了积分攻击和不可能差分攻击。结果显示9轮µ2算法不能抵抗积分攻击，11轮µ2算法不能抵抗不可能差分攻击。另外，本文对µ2算法抵抗差分攻击的能力进一步评估，证明了µ2算法的4轮差分特征的最大概率为 2-39， 比设计报告中的2-36更为紧致。本文的结果完善了对µ2算法抵抗积分攻击、差分攻击和不可能差分攻击能力的评估，结果显示µ2算法对上述攻击仍存在一定的安全冗余空间。如何考虑更多的设计细节从而给出更长的不可能差分以及如何利用已经得到的区分器进行更长轮数的攻击是下一步工作的重点。