基于FPGA的图着色问题求解

张益豪 张子超 刘小青② 冷 煌② 王之元 许 进②

①(北京大学信息科学技术学院 北京 100871)

②(北京大学高可信软件技术教育部重点实验室 北京 100871)

③(国防科技创新研究院人工智能研究中心 北京 100073)

1 引言

图着色问题是计算机科学中的一项重要研究内容，不论在理论还是应用方面均具有重要的研究价值。例如，图着色问题可应用于求解第4代移动通信系统中设备到设备通信的资源分配问题[1]，将大量目标程序分配给少量中央处理器(C e n t r a l Processing Unit, CPU)中寄存器的寄存器分配问题[2]，在满足一定约束条件下的时间表安排问题等[3]。尽管图着色问题在实际生活中应用广泛，但该问题属于NP-完全问题，因此如何寻找精确算法来求解NP-完全问题一直是近年来研究的热点[4]。然而，NP-完全问题的一个重要特性是如果采用穷举法求解，随着问题规模的增加，时间复杂度将会以指数级增长[5]。因此，一些算法被提出以降低求解图着色问题的时间复杂度，常见的算法包括动态规划、分支定界、整数线性规划以及回溯法。

动态规划、分支定界与整数线性规划均可求得图着色问题的一组解，但有时求得图着色问题的所有可行解是有意义的。例如，当一个图G=(V,E)存在一条割边e=时 ，其中V={v1,v2,...,vn}是由顶点vi构成的集合且E={e1,e2,...,em}是由边ei构成的集合，则G-e的两个连通分量可以作为两个图分别进行图着色。此时，由于G-e的两个连通分量仅通过割边e=连接，因此只要vs与vt的 颜色不同，就能够得到原图G的一组有效着色方案。若G-e的两个连通分量着色完成后vs与vt的颜色相同，则可通过置换函数改变任一连通分量的着色方案，使得vs与vt的颜色不同。回溯法[11]一般用来求解图着色问题的所有解，其基本思想是以深度优先搜索整个解空间，同时通过剪枝来减小所需搜索解空间的大小。

通常求解图着色问题的算法是在通用处理器上利用软件所实现的。然而，随着顶点规模的增加，通过软件实现图着色算法会造成通用处理器性能的下降以及能耗的提升。尽管已经存在许多软件解决方案来提高求解图相关问题的性能与能量效率，但当前通用处理器的硬件结构仍然是影响性能和能量效率的一个重要因素[12]。现场可编程逻辑门阵列(Field Programmable Gate Array, FPGA)是由可配置逻辑块(Configurable Logic Blocks, CLBs)，输入输出(Input/Output, I/O)模块与可编程的互连资源所构成的可编程逻辑电路[13]。FPGA具有能耗低，开发周期短，易于对设计中出现的错误及时修正，以及适用于实时性系统和分布式系统等特点[14]，因此与图相关的问题能够基于FPGA设计专用硬件电路来求解[15]。

2 图着色问题的回溯算法

回溯法求解图着色问题的思路是对图的所有可能着色方案进行搜索，并判断着色方案是否满足相邻顶点所分配的颜色不同。以未着色的图作为根节点，依据图中顶点与顶点之间的邻接关系和深度优先搜索策略，从根节点出发遍历图中的每个顶点，从而对解空间进行遍历。在每一次访问图中节点的过程中，需要判断当前节点是否存在满足图着色问题约束的着色方案。若存在满足约束的颜色，则对该节点进行着色并从该节点继续遍历未访问的节点；若不存在满足约束的颜色，则逐层向该节点的祖先节点回溯，从而完成剪枝，避免对以该节点为根节点的子树进行搜索。

接下来本文以对图1中的平面图进行四着色为例说明回溯法的流程。在图1中，数字表示顶点标号。利用回溯法，可以得到图1的24种着色方案，如图2所示。详细来说，图2中树的根节点(树的第1层)表示所有的顶点均未着色，树的第i层表示已有(i-1)个 顶点着色，且连接第i层 与第(i+1)层边的颜色表示顶点i被分配的颜色。假设先用红色对顶点1进行着色，当对顶点2进行着色时，由于顶点1与顶点2连接，若为顶点2分配红色，则相邻顶点具有相同的颜色，此时不满足图着色问题的约束。因此只能用绿色、紫色、咖啡色之一对顶点2进行着色。若存在所有着色方案均无效的顶点，则返回该顶点的父节点，改变父节点的着色方案。

图1 四顶点平面图

由图2可以看出，图1的四顶点平面图共有24种着色方案。然而，给定任意一种着色方案，剩余的着色方案可以根据置换函数得到。图1的色组划分[16]是唯一的，则其独立着色方案集(其中任意一个方案都不能通过其他着色方案经置换函数得到)仅有1个元素。因此，如果利用回溯法仅求取独立着色方案集，可以减小搜索解空间的大小。除此之外，在FPGA中，存储容量主要由随机存取存储器(Random Access Memory, RAM)的大小决定。FPGA内部的RAM由块RAM(Block RAM)和分布式RAM(Distributed RAM)组成[17]。给定FPGA型号，Block RAM的大小是固定的。Distributed RAM由查找表(Look Up Table, LUT)构成，会占用FPGA内部大量的逻辑资源[18]。因此相比于通用处理器，FPGA内部的存储资源受限[19]。随着图的顶点数逐渐增大，求取所有的四着色方案不仅会增加时间复杂度，也有可能造成需存储解的个数以指数级增长。因此，为了减小在FPGA内部存储所求解的数量，需要求取图的独立着色方案集。

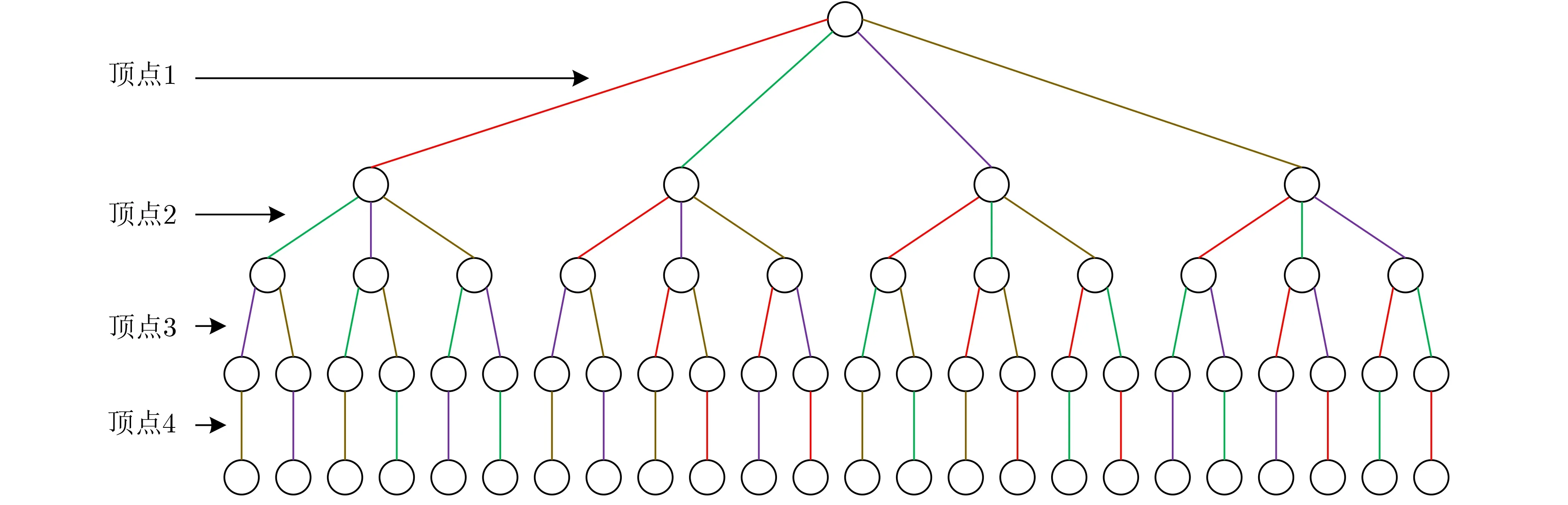
图2 四顶点平面图的着色方案

令Kn′表示n′个顶点的完全图，由于任意两个顶点之间都存在一条边，则要使Kn′满足图着色问题的约束，至少需要n′种颜色。因此一个S-可着色的图G只能含有n′≤S的完全子图Kn′，其中n′≤S。若图G的最大完全子图顶点数为T，则将图G记为GT。首先利用T种颜色对任一最大完全子图中的T个顶点着色并固定这T个顶点的着色方案。接下来利用回溯法对GT中剩余顶点进行着色，则能够有效避免图着色问题中解的同构性。综上所述，依据图G的最大完全子图的顶点数，可将图G分为不同的类型。例如，4-可着色图可以分为G2,G3,G4。算法的流程图如图3所示。

图3 回溯法算法流程图

3 基于FPGA的图着色实现方案

FPGA通常自顶向下地设计层次化及正则化的模块，其中正则化设计指的是最大化利用已设计的模块以提高模块的复用率。每个模块具有不同的功能，通过上层模块对下层模块的调用来实现最终的功能函数。合理地设计模块划分可以将复杂的问题转化为较小的问题，从而简化设计的复杂度[20]。本文将基于回溯法的图着色问题求解分为3个模块，分别是输入模块、核心计算模块与输出模块，如图4所示。3个模块共享时钟源信号clk与低有效复位信号rst_n。接下来以图的四着色问题为例说明该流程图。

图4 基于FPGA的图着色实现方案

在输入系统中，输入信号data_in由两部分组成：图G的邻接矩阵与图类型G2,G3,G4的表示信号initial_state，其中initial_state是两比特的信号，01, 10与11分别表示G2,G3与G4。图类型表示信号initial_state代表图G的最大完全子图，而求解图G的最大完全子图也属于NP完全问题。为了简化求解的复杂度，本文在通用处理器上采用启发式算法求取图G的最大完全子图。值得注意的是，即使求取图G的完全子图并不是最大的，只会造成FPGA内部所需存储解的个数增加，而不会影响图着色问题的求解。图G的邻接矩阵通过串行的方式传输到输入系统中，输入系统利用一块RAM实现串并转换：RAM中每一个地址ram_addr_rd对应一个顶点，而ram_addr_rd对应的值为与该顶点相邻的信息。即输入系统通过从核心计算系统获得ram_addr_rd来确定当前正在对哪个顶点进行着色，而输入系统根据ram_addr_rd读取RAM中代表该顶点邻域信息的data_internal信号并传送给核心计算系统。输入信号的有效使能data_en用来表明输入数据中哪些信号是有效的。在系统初始化时，核心计算系统处于空闲状态，而当输入模块接收整个邻接矩阵与图类型信号后，用来表示信号已接收完成的一个脉冲信号initial_en被传送给核心计算系统，表明核心计算系统可以开始进行图着色的相关运算。

在核心计算系统中，当接收到initial_en信号后，根据图的类型信息initial_state对前T个顶点进行固定的着色初始化。通过ram_addr_rd信号来控制从输入系统中读取哪个顶点的邻域信息。核心系统中增加一个信号v_color_yn表示对应的顶点是否被着色。若未着色则从第1种颜色开始尝试，若已着色则根据当前着色计算下一个可能的着色方案color_next。结合data_internal，v_color_yn和color_next来判断当前顶点的邻接顶点是否存在相同的着色。若不存在则将color_next赋值给包含所有顶点着色方案的信号color_vector，若存在则依据color_next的值决定是否需要回溯。回溯的操作可以通过改变ram_addr_rd的值来回溯到当前节点的父节点。若核心计算系统通过运算得到一种有效的四着色方案时，则将着色方案信号color_vector和表示着色方案有效的使能信号result_en传送到输出系统进行保存。当所有的着色方案完成遍历后，核心运算系统会将done_en信号置为有效位，表明所有运算已结束。若运算已结束并且result_en始终无效，则说明当前图不存在有效的着色方案。由于图着色方案可能存在大量的解，而解的数量无法预先得知。同时，FPGA内部用来存储解的RAM是预先固定好的，且FPGA内部能够用来存储的RAM 容量受限。因此当输出系统无法保存新的着色方案时，需要置full_en有效，使核心系统停止当前的运算，并保存当前运算的信息。待输出系统中的RAM有新的存储空间接收着色方案时，置full_en无效，此时核心计算系统继续进行之前的运算。注意到回溯法中每一次迭代的主要步骤是验证当前节点的着色与其邻接节点的着色是否相同，该验证可以通过或运算实现。即只要存在一个邻接顶点的着色与当前节点的着色相同，则当前节点无法着色，需要改变着色方案或进行回溯。

在输出系统中，result_en信号用来判断当前着色方案color_vector是否有效。若有效则将color_vector存储在RAM中，若当前RAM中存储的着色方案个数已达到最大值，则置full_en有效，使得核心计算系统停止当前运算。根据输入使能信号output_en与output_en_all来决定是否将RAM中的着色方案输出，其中output_en 1次只输出1个有效着色方案，而output_en_all一次性将所有着色方案全部输出。RAM中存储的着色方案通过并串转换生成data_out信号输出，使能信号data_out_en用来表明当前输出是否有效。注意到图着色问题可能无解，因此本文利用信号solution_yn表示该图是否存在有效的着色方案。

4 硬件实现

本文在型号为EP4CE6E22C8的FPGA上，利用Verilog语言实现了基于回溯法的图的四着色问题求解。在Altera平台的Quartus Prime 18.0的开发环境中经过综合后，得到图的顶点个数与FPGA内部资源消耗的关系，如表1所示。在表1中，本文采用逻辑元件(Logic Element, LE)和寄存器的个数来表示FPGA内部的资源。LE是构成FPGA中CLB模块的重要单元，通常用来实现逻辑电路[21]。不同的FPGA型号会有不同数量的LE，例如EP4CE6E22C8仅有6000个LE，而Stratix GX10M拥有10200000个LE[22]。由表1可以看出FPGA内部的资源LE与寄存器均基本与图的顶点个数成正比，造成这种现象的主要原因是表示顶点是否被着色的信号v_color_yn与顶点着色方案信号color_vector所需的比特数与顶点数成正比，且验证当前节点着色方案与邻接节点着色是否相同是通过或运算实现的，而或运算的操作数是color_vector。表1的资源消耗主要用于实现图4的输入系统、核心计算系统与输出系统。但在输入输出系统中并不包含用于和外部通信的传输协议模块。

表1 FPGA资源消耗

接下来以12顶点的图四着色为例，分析基于FPGA的图着色算法性能。进行静态时序分析后，得到当FPGA内核电压为1.2 V，温度为85°C时，系统允许工作的最大时钟频率为139.65 MHz，而当FPGA内核电压为1.2 V，温度为0°C时，系统允许工作的最大时钟频率为147.17 MHz。由图3的回溯算法流程图可知，算法的运行复杂度由改变顶点着色方案的次数和每次迭代时判断能否着色所消耗的时间共同决定。由于在FPGA平台上实现图着色算法不能减小改变顶点着色方案的次数，因此仅需考虑回溯法中每次迭代所消耗的时间。图5可以看出每次color_next的改变最多仅需10个时钟周期，注意到每次顶点着色方案的改变所需时间周期并不固定，这是因为除了判断当前着色方案是否有效外，还需根据是否回溯改变ram_addr_rd以选取当前着色的顶点。因此，若FPGA内部使用100 MHz的时钟，则每次迭代所消耗的时间为10/100=0.1 μs。同时，在主频为3.0 GHz的通用处理器中，利用Matlab对1000组12顶点的图进行四着色，平均每次迭代所消耗的平均时间为5.397 μs。由此可见，相比于在通用处理器中采用软件实现图着色算法，基于FPGA实现的图着色算法执行速度更快。若采用性能更高的FPGA，可以进一步提高系统允许工作的最大时钟频率，从而减小基于回溯法求解图着色问题的时间。

图5 顶点着色方案验证的功能仿真

随着顶点个数的增加，在每次迭代中判断当前着色方案是否有效所需的运算量增加。具体来说，利用3个周期的或运算来判断当前顶点的着色方案是否与邻接节点着色方案相同。本文基于空间换时间的思想，通过增加单个周期内或运算的个数，保证每次迭代时FPGA内部运算所需时钟周期个数与顶点的个数无关。因此随着顶点个数的增加，每次color_next的改变仍然仅需10个周期，且每次迭代时FPGA执行运算所消耗的时间与顶点个数无关。而随着顶点个数的增加，每次迭代时软件实现方案会消耗更多的时间。例如当图的顶点个数为512时，利用Matlab实现每次迭代所消耗的时间为15.611 μs。

为了验证所实现硬件的正确性，本文基于通用异步收发传输器协议实现了FPGA与通用处理器之间的通信。对具有如图6所示邻接矩阵A的12顶点图G进行着色。根据该图的类型，通用处理器需将146 bit信息传输到FPGA中，其中前144 bit为邻接矩阵A的1维表示，最后2 bit信息是表示图类型的initial_state信号。基于16进制将该146 bit表示为961186010D2B29AA59029BB2E582DD24622 D01，并将该信息通过串口传输到FPGA内部进行运算。通过将FPGA运算的结果与通用处理器中图着色的运算结果对比，验证了FPGA内部输出的解是具有邻接矩阵A的图G的所有独立着色方案集。

图6 12顶点图的邻接矩阵

5 结束语

图着色问题一直是近年来研究的热点问题，本文基于FPGA利用回溯法实现了图着色问题的求解。首先利用最大完全子图固定了部分顶点的着色，使得图着色问题的解是独立着色方案集。随后在Altera公司的EP4CE6E22C8芯片上设计并实现了基于回溯法的图着色问题求解。最后的实验结果表明，基于FPGA的图着色算法在每次迭代时，判断能否着色所消耗的时间小于在通用处理器中利用软件实现迭代所需的时间，并且FPGA内部所消耗的资源与图的顶点个数成正比。