基于北斗卫星导航系统非组合精密单点定位算法的精密授时精度研究

2022-09-22马祥泰史增凯钱昭勇胡彦逢董绪荣

电子与信息学报 2022年9期

马祥泰史增凯钱昭勇胡彦逢董绪荣

(航天工程大学航天信息学院北京 101416)

1 引言

“导航”、“定位”与“授时”(Positioning,Navigation and Timing, PNT)体系构建是中国近些年来最重要的国家战略之一[1]，而全球导航卫星系统(Global Navigation Satellite System, GNSS)具有全球性、全天候和高精度的特点，成为了国家综合PNT体系中关键的组成部分[2]。此外，随着信息时代的发展，电力系统、金融系统、通信系统等对授时精度的要求也越来越高，而传统授时方法如网络时间协议(Network Time Protocol, NTP)受到计算能力和存储空间的限制，远距离校准精度不高。因此，基于GNSS的精密授时研究得到了广泛关注[3,4]。

传统的GNSS精密授时技术是基于伪距单点定位原理，由于伪距观测噪声较大，其精度仅能达到纳秒级。伴随着精密单点定位(Precise Point Positioning, PPP)技术的发展，它在时间传递和授时领域也得到了一定的应用[5,6]。张小红等人[7]开展了全球定位系统(Global Positioning System, GPS)PPP时间传递实验，静态实验结果表明时间传递精度在0.1～0.2 ns；同样地，文献[8]计算得到的GPS单系统精密授时精度最高也可达0.1 ns。但是，他们的处理策略仅适用于事后处理，不能实时评估授时精度。针对多系统星座[9]，文献[10]分析了GPS单系统和GPS + 格洛纳斯(GLObal NAvigation Satellite System, GLONASS)计算的时间传递情况，结果表明两种方案的授时精度类似，即GPS +GLONASS多系统组合方案并没有提高授时精度。电离层延迟也会对授时精度造成影响，文献[11]对比评估了无电离层，经电离层校正和受电离层约束的3种单频精密单点定位(Single Frequency Precise Positioning System, SF-PPP)模型，结果表明电离层约束模型授时精度优于另外两种模型,同时还考虑到了高度角对授时精度的影响。参照消电离层组合模型，闫伟等人[12]研究了非组合PPP模型在精密授时中的可行性，推测其在运动载体精密授时方面具有较大价值，但是他们仅考虑了静态和静态仿动态两种场景。总之，现有基于GNSS PPP技术的精密授时方法仍存在一些亟需解决的问题：(1)现有PPP技术大部分是基于消电离层组合模型，但是它利用了伪距和载波相位观测值的线性组合，组合噪声较高，从而影响了授时精度；(2)大部分研究是基于GPS，而伴随着北斗三号系统的建设及开通[13]，信号质量得到极大提升[14]，基于北斗卫星导航系统(BeiDou navigation Satellite system, BDS)的精密授时研究具有重要意义[15]；(3)现有研究多是针对静态场景或采用静态模拟动态场景，因此在处理载波相位周跳时多是采用事后处理的方式，且授时精度解算时也采用国际GNSS服务(International GNSS Service, IGS)发布的事后精密星历等，不能满足动态条件下实时解算的要求[16]。

本文首先介绍了传统消电离层组合PPP模型；其次，针对消电离层组合造成噪声放大的问题，引入了非组合PPP模型，并分别采用Kalman滤波中的静态模型和动态加速模型开展时间传递解算；再次，给出了精密授时精度实时处理策略，并分别对静态场景和车载实时动态场景下的BDS精密授时精度进行了解算，而且与GPS做比较；最后，给出论文的主要结论。

2 模型介绍

2.1 消电离层组合PPP模型

消电离层组合PPP模型通过将两个不同频率的观测值进行线性组合，消除了载波相位和伪距观测值上的1阶电离层延迟项，只估计接收机坐标、接收机钟差、天顶对流层延迟和模糊度4类参数[7]

2.2 非组合PPP模型

尽管消电离层组合能够消除电离层1阶项的影响，但是在观测方程式(1)和式(2)中，新的观测值由原始单频点伪距或载波相位观测值组合而来，因此观测噪声会变大。随着PPP技术的发展，研究者们提出了非组合PPP模型，其观测方程为[12]

非组合PPP模型增加了电离层参数，其余噪声方差与消电离层组合PPP类似。假设各个频点下的伪距、载波相位观测值相互独立，那么单历元观测值的随机模型为

在非组合PPP中，电离层延迟项被当作未知参数进行估计，它通常被描述为1阶高斯马尔科夫随机过程，即

不同于消电离层组合，非组合PPP模型中的原始噪声不会被放大，但相应地，它增加了电离层延迟等未知参数，计算复杂度也更高。尽管BDS与GPS的非组合PPP模型是一致的，但是两种系统本身具有不同的特点--信号体制、轨道类型和星座构型等均不相同，因此开展BDS精密授时研究是必要的。

2.3 参数估计

在非组合PPP定位解算时，Kalman滤波不需要保留前面的数据，只需要上一个历元的状态和当前历元的观测值就可以递推出新的状态估值。Kalman滤波的状态模型和观测模型为

Kalman滤波分为预测和更新两个过程，其中预测部分基于上一个历元的估计值及状态转移矩阵推导下一个历元的状态向量；更新部分再根据当前历元的观测值，对预测部分得到的状态向量进行更新[18]。Kalman滤波常用的运动模型有如下3种：(1)静态模型，即接收机静止不动，速度为0；(2)匀速运动模型，接收机载体做匀速运动，速度为恒定值，加速度为0；(3)动态加速模型，接收机载体做加速度变化的变速运动。其中，在静态模型中，Fpos为9×9单位矩阵；在匀速运动模型，它为

根据后文实验场景的实际情况，本文采用静态模型和动态加速模型进行相关分析。

3 静态PPP精密授时实验研究

3.1 数据采集与处理策略

本节首先对BDS静态PPP精密授时精度开展研究，并与GPS进行比较。为此，本节选取了2019年10月1日6个IGS测站的双频观测数据，分别研究了静态条件下消电离层组合和非组合PPP模型的授时精度。其中，6个外接原子钟的测站分别为GMSD,KARR, KZN2, MAYG, URUM和WUH2，数据采样间隔为30 s。所选监测站的基本信息列在了表1中。

表1 静态实验所用IGS监测站的基本信息

本文以IGS精密钟差文件中的监测站钟差作为真值，分析不同PPP模型解算出的接收机钟差精度。静态实验采用的数据采样间隔为30 s，而IGS精密钟差间隔为5 min，因此，本文将每5 min解算得到的钟差与精密钟差进行对比。消电离层组合PPP模型的处理策略见表2，且在参数估计时以单点定位(Single Point Positioning, SPP)的结果作为初始值。两种模型均使用双频原始观测数据。两个频点分别是BDS B1[19], B3和GPS L1, L2。Kalman滤波过程中噪声、方差或协方差的选择通常是基于经验的，比如当电离层活跃时，方差赋较大值；当电离层稳定时，方差赋较小值。基于选取的静态数据，本文选择的量测噪声、过程噪声和估计误差方差的初值也列在了表2。此外，非组合PPP模型还需要增加电离层延迟项，其初始值设置为0 m，初始标准差设置为1×102m，电离层延迟过程噪声为1×10-2。

表2 静态消电离层组合PPP模型处理策略

3.2 静态PPP精密授时结果与分析

PPP中位置估值的精度会影响钟差参数估计的精度。因此，为评估静态非组合PPP位置解算精度，本节将其解算出的位置坐标与IGS提供的监测站参考坐标作差。各测站E, N, U方向上位置估值差值的均方根(Root Mean Square, RMS)值和标准差(STandard Deviation, STD)分别见表3和表4[20]。

由表3、表4可以看出，收敛后各测站E, N, U各方向RMS值分别在0.02 m, 0.01 m, 0.04 m左右。各测站E方向的STD均在1 cm以内，N方向的STD在5 mm以内，只有U方向的STD最高可达4 cm。这都表明静态非组合PPP模型解算结果内符合精度高。由此可知，BDS和GPS定位精度相当，在亚太地区尤其是在中国境内，BDS的定位精度要高于GPS。

表3 BDS/GPS各测站E, N, U方向RMS值(m)

表4 BDS/GPS各测站E, N, U方向的STD(m)

接下来分别采用消电离层组合PPP(经典PPP)和非组合PPP模型解算接收机钟差，并和IGS提供的精密钟差文件对比，得到各测站接收机的钟差误差如图1所示，其中消电离层组合的参数估计参照朱荷欢等人的方法[8]，静态条件下的载波相位模糊度采用固定解。由于IGS提供的监测站精密钟差产品是基于GPS时间系统的，因此BDS解算出的钟差与IGS提供的精密钟差存在系统误差。考虑到系统误差后，表5只给出了GPS静态PPP钟差误差的RMS值，而不同PPP模型计算出BDS, GPS的钟差误差的STD见表6。

由图1、表5和表6可知，对GPS而言，消电离层组合PPP算法和非组合PPP算法的RMS值分别在0.33 ns, 0.26 ns以内，同样非组合PPP算法钟差解误差的STD优于消电离层组合PPP算法，分别在0.18 ns和0.32 ns以内；对BDS而言，消电离层组合PPP算法和非组合PPP算法钟差解误差的STD分别在0.22 ns和0.19 ns以内：这说明静态条件下GPS和BDS非组合PPP算法精度高于消电离层组合PPP算法。对比BDS, GPS，加之考虑到BDS与GPS定位精度相当，在亚太地区定位精度甚至高于GPS，因此断定BDS静态精密授时精度略高于GPS；对比两种PPP算法，消电离层组合PPP和非组合PPP解出的钟差误差大部分相差在0.1 ns以内，但非组合PPP算法的精密授时精度优于消电离层组合PPP算法。但是从图1还发现在某些时段内，KZN2, WUH2中两种PPP模型解算出的钟差存在较大差别，下面逐个对其开展分析。

表5 GPS静态PPP钟差误差的RMS值(ns)

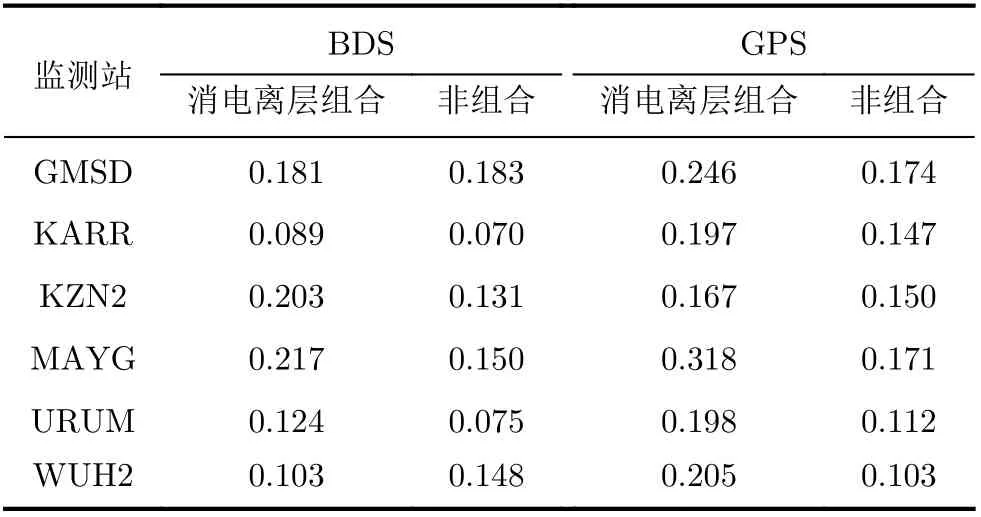
表6 BDS/GPS静态PPP钟差解误差的STD(ns)

图1 BDS/GPS中经典PPP、非组合PPP模型解算的钟差误差

KZN2, WUH2在观测期间的卫星数量和空间位置精度因子(Position Dilution Of Precision,PDOP)如图2所示。结合图1，从KZN2钟差解算结果可知，某些时间段BDS两种PPP模型解算出的钟差出现了较大的非系统性偏差，而从图2可知，在06:00～08:00, 16:00, 20:00左右的时间段，BDS有效卫星数发生变化，PDOP突然增大。因此，本文认为这是造成两种PPP模型解算出的钟差差别较大的原因。

WUH2站位于我国中部的武汉市，该站观测到的BDS导航卫星数量最高可达17颗，远高于观测到的GPS导航卫星。因此，结合图1和图2，BDS的PDOP普遍低于GPS，且BDS解算的钟差误差大部分在0.3 ns以内。对WUH2而言，BDS两种PPP算法和GPS消电离层组合PPP算法的钟差误差在某些时间段也都出现了较大的起伏，尤其是在10:00,12:00, 14:00, 16:00以及20:00前后。对应图2可知，这些时段BDS的PDOP均出现突变，进而导致相应的钟差解算误差增加。同样地，GPS 04:00～08:00之间和16:00左右，钟差误差也出现了相似情况。

图2 KZN2, WUH2在观测期间的卫星数量(NSAT)和PDOP

4 动态PPP精密授时实验研究

4.1 数据采集与处理策略

当前精密授时精度的相关研究多是集中在静态条件下，动态分析多是采用静态模拟动态来实现。因此，为了更完备地分析PPP在动态情况下的精密授时精度，本节开展了车载动态实验研究。实验开展于UTC时间2019年5月16日，全程约50 km，总时长约3 h 30 min，共采集到约12900个历元时刻的数据。实验采用Novatel接收机，采样间隔为1 s，卫星截止高度角设置为10°。考虑到实时性要求，本节基于超快速预报星历对车载数据进行PPP钟差解算，参数估计和处理策略如表7所示，天线相位偏差采用Igs14.atx修正，其他与静态PPP相同。对于载波相位模糊度，当汽车加减速或信号被遮挡时采用浮点解，其他情况下采用固定解。同时，本文选择的量测噪声、过程噪声和估计误差方差的初值也列在了表7。其余参数与第3节相同。

表7 动态PPP中参数估计处理策略

4.2 动态PPP精密授时结果与分析

车载实验中接收机没有外接原子钟，加之考虑到PPP事后双向滤波解的精度高于实时动态PPP解，因此本节把事后PPP双向滤波解算的钟差作为接收机钟差的“真值”，来分析实时动态PPP的授时精度。动态PPP钟差误差的RMS, STD和均值见表8。

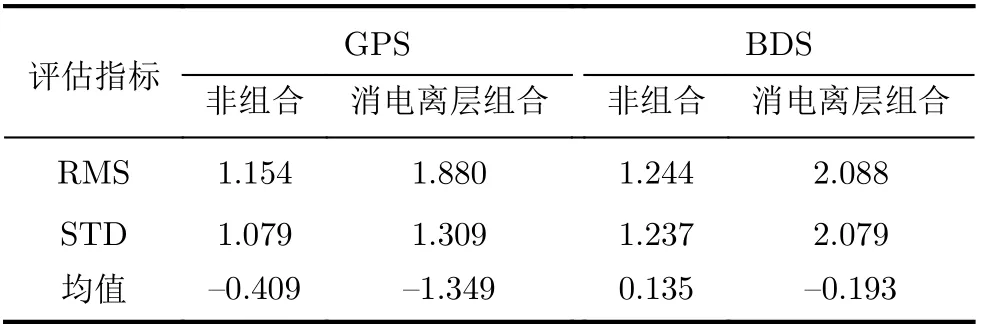
表8 动态PPP钟差误差RMS, STD和均值(ns)

由表可知，BDS和GPS采用预报星历时实时动态PPP钟差解算精度在2 ns以内；GPS授时精度略高于BDS，非组合PPP算法精密授时精度高于消电离层组合PPP算法。而且非组合PPP算法钟差解更平稳、可靠。

为了进一步分析动态PPP算法精密授时的精度以及影响钟差解算的原因，接下来本节对BDS, GPS解算时的卫星数量、PDOP、接收机钟差精度因子(Time Dilution Of Precision, TDOP)以及解算的车辆速度进行统计，分析影响钟差解算精度的原因。BDS, GPS解算中有效卫星数量、PDOP值、TDOP值以及车辆在平面的运行速度和钟差项中误差如图3、图4所示。

从图3和图4知，对于BDS单系统，实验过程中的大部分时间可以观测到8～10颗BDS导航卫星；PDOP值大部分时间小于3；车辆最高速度为14 m/s，最低速度为0 m/s。对于GPS单系统，实验过程中的大部分时间可以观测到8～10颗GPS导航卫星，最多12颗，其中在02:50～03:40时段，可用卫星数减少到8颗以下；PDOP值大部分时间小于2.5。对比不同历元时钟差项中误差及相应的车辆速度、卫星数量可知，当车辆突然加速、减速，或者道路开阔性不好时，会出现卫星失锁的情况，导致观测值变少以及模糊度重收敛，进而影响到授时精度。对于非组合PPP模型，钟差误差均在2 ns以内，完成收敛后，BDS和GPS钟差项中误差分别小于0.4 m和0.3 m。消电离层组合PPP模型重收敛速度低于非组合模型，但是由于观测值组合放大了噪声，总体上钟差项中误差大于非组合PPP模型，且钟差误差大于非组合PPP模型的钟差误差。对比BDS和GPS两个系统钟差解算精度，由于GPS卫星数量相对稳定，不易失锁从而不需频繁重收敛，因此GPS钟差解算精度要高于BDS。但当两个系统在完成收敛且不发生重收敛的情况下，BDS和GPS钟差解算精度相当，钟差项中误差均在0.3 m以内。非组合PPP模型由于使用原始观测数据，避免了数据组合带来的噪声放大，因而精密授时精度高于消电离层组合PPP模型。总之，非组合PPP算法比消电离层组合PPP算法更平滑、稳定，其钟差解同事后PPP双向滤波解算的钟差结果更吻合。