基于混合粒子群算法的计算卸载成本优化

周天清 曾新亮 胡海琴

(华东交通大学信息工程学院 南昌 330013)

1 引言

近年来，随着移动终端(Mobile Terminal,MT)的爆发式增加，以及自动驾驶、人工智能、虚拟现实/增强现实(VR/AR)等急需计算资源且对时延有极高要求的计算密集型业务的不断增长，给资源受限的移动计算系统和无线通信网络带来了前所未有的挑战[1,2]。

移动边缘计算(Mobile Edge Computing,MEC)通过将计算和存储资源部署在网络边缘，允许MT将计算任务卸载到边缘服务器，为用户提供了超低时延、高带宽的网络服务[3]。但是，由于无线和计算资源有限，如果太多的MT将其计算任务卸载到MEC服务器，会导致严重的网络计算拥塞和干扰[4]。超密集异构网络[5]通过在宏小区中部署更为密集的小基站(Small Base Station, SBS)并与MEC相结合，能进一步缩短MT与MEC服务器间的距离以降低传输时延及支持海量链接。

时延和能耗作为计算卸载性能评估的重要指标，近年来得到了深入的研究。文献[6]提出了一种延迟感知计算卸载算法，联合优化保密配置、计算卸载和无线资源分配，以最大限度地减少整体执行延迟。文献[7]在超密集网络场景下对卸载策略、信道资源和传输功率进行联合优化，以最小化系统能耗。文献[8]建立SBS和宏基站(Macro Base Station,MBS)之间的无线回程链路以实现共享频谱的目的，并最终最小化能耗和执行时间的加权和。但是上述研究或是利用单个MEC服务器来满足传入的卸载请求，或是未实现MEC服务器计算资源的合理利用。而对于多MT的场景，MEC服务器很容易拥塞，这将直接影响用户体验。

鉴于此，越来越多的研究倾向于多MEC服务器的场景。文献[9]在多用户和多MEC服务器场景下，联合优化计算卸载和资源分配策略以最小化MT能耗。文献[10]在能量约束下，通过优化卸载决策和计算资源分配以最大限度地降低超密集网络中MT的计算延迟。进一步，为更合理分配网络及计算资源，研究者开始关注卸载成本问题。文献[11]针对非正交多址接入的车载边缘计算网络，联合任务卸载、用户分簇和计算资源块联合优化以最小化任务处理成本问题。文献[12]研究了基于边缘计算的车联网，通过优化任务的卸载时间、无线带宽分配和计算资源分配来最小化系统的计算与通信成本。文献[13]为了最小化系统的计算和通信成本，提出了一种具有垂直和水平卸载的4层云边缘计算系统。虽然文献[11-13]考虑了任务卸载时所需支付的计算和通信费用，但未连同任务在本地计算时产生的开销一起考虑。

不同于上述研究，本文研究了融合MEC的超密集异构网络下多小区多用户的计算卸载问题，将联合执行计算卸载和计算资源管理，并在相同的带宽利用率下最小化用户的任务处理成本。其中，任务处理成本由本地能耗开销、无线频谱占用开销和边缘计算资源租用开销3部分组成。本文的主要贡献总结如下：

(1)在融合MEC的超密集异构网络中，将用户任务处理所需支付的费用作为计算卸载成本，联合无线资源、计算资源管理，满足时延约束的同时，使所有用户的任务处理成本最小化，并建立相应的问题模型。

(2)设计了混合粒子群优化(Hybrid Particle Swarm Optimization, HPSO)算法来解决上述非凸问题，该算法先后执行多样性增强(Diversity Enhancement, DE)的自适应遗传算法和自适应粒子群算法。但不同于文献[14]中的分层自适应搜索(Hierarchical Adaptive Search, HAS)算法，HPSO算法引入了部分参量的规范化处理，且改变了粒子群算法的权重更新规则以提升粒子群算法的收敛速度。此外，与[4,14]不同的是，为更合理地分配MEC服务器的计算资源，HPSO算法改进了遗传算法中的资源块初始化操作，并由此引进了计算资源块按需分配策略。最后，通过仿真验证了本文所提算法优越性。

2 系统模型

2.1 网络模型

超密集异构边缘计算网络的系统模型如图1所示，每个六边形的蜂窝网格包含1个宏基站(MBS)、N个微基站(SBS)和K个MT，并且每个基站配有一个MEC服务器。不失一般性的情况下，本文考虑一个MBS的场景。假设基站的索引集合为N={1,2,...,n,...,N,N+1}，其中MBS的索引为N+1，MT集合表示为K={1,2,...,k,...,K}。

考虑到SBS的小范围覆盖和超密集部署，为降低控制开销，SBS的控制信令可由MBS负责处理。类似文献[14]，本文亦将频带分割为控制面和用户面，其中控制面用于传输控制信令，用户面用于传输数据。由于计算卸载发生在用户面，因此计算卸载机制研究时仅需关注此平面。在图1中，MT可以选择将自己的数据任务上传至SBS或者MBS上进行处理，亦可自身完成计算任务。值得注意的是，MBS不仅需要处理网格中的所有控制信令，还需处理由MT上传的数据，而SBS仅需完成数据处理任务。在计算卸载过程中，对于任何任务，如果其本地计算时延小于任务截止时间，MT会选择本地计算以降低额外开销，否则MT将任务上传至基站进行计算以减少时延，保证满足时延约束。

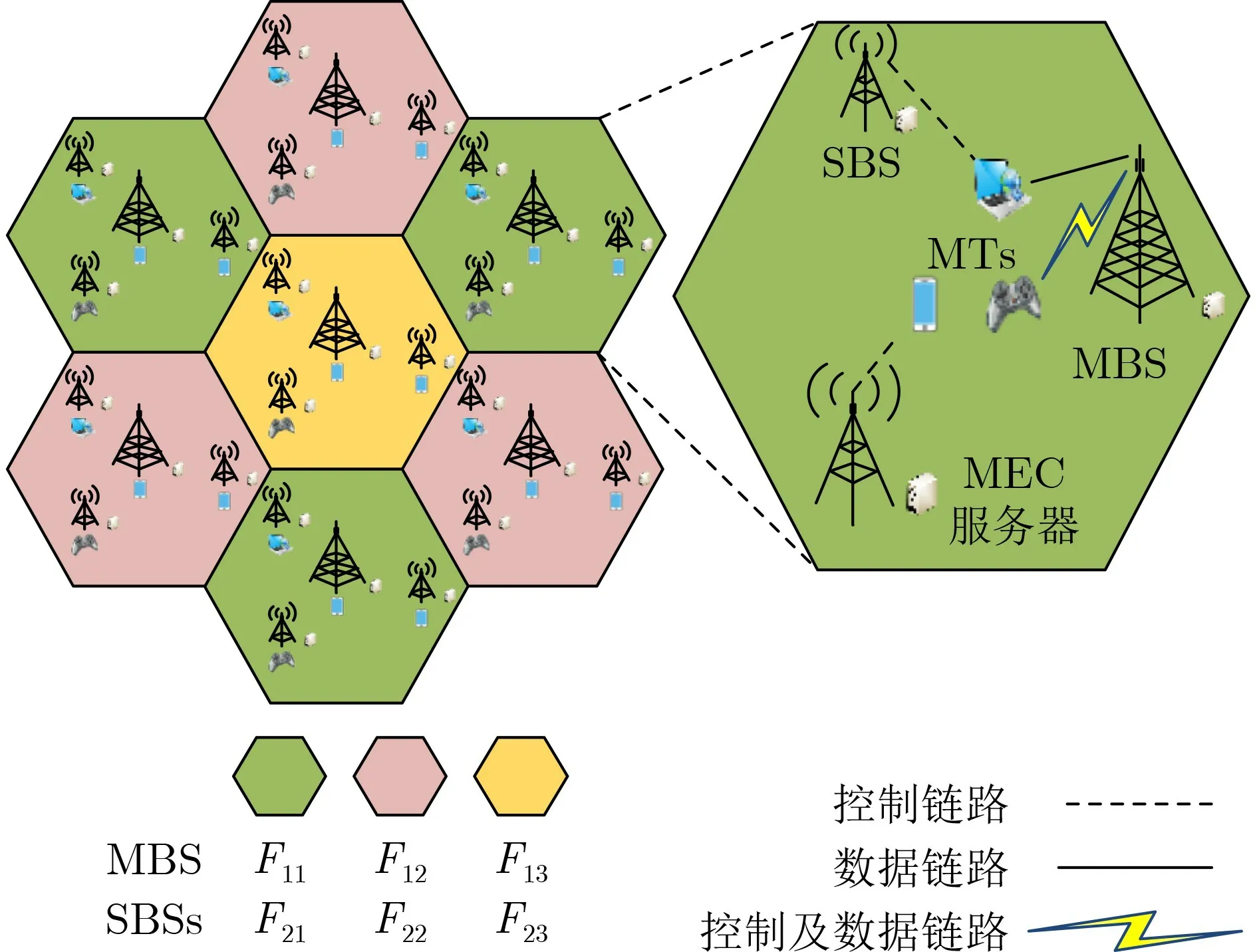
图1 系统模型

一般来说，计算卸载包括以下3个阶段。首先，MT的计算任务通过无线信道上传到BS上；然后，BS执行计算任务；最后，BS反馈计算结果给MT。考虑到计算结果的数据量相对较小，反馈过程可忽略不计。

2.2 资源模型

如图1所示，每个宏小区内所有小基站形成一个簇。为消除层间和层内的干扰，用户面所用频带F被划分为F1和F2两部分以分别供宏基站和小基站使用，其带宽分别为µW和( 1-µ)W，其中µ表示频带划分因子。为了消除宏基站间的干扰，频带F1被 再次划分成3个子带F11,F12和F13，即相邻宏小区中的宏基站的频带带宽为µW/3。为了消除小基站簇之间的干扰，频带F2同样被再次划分成3个子带F21,F22和F23。进一步，为消除簇内小基站间的干扰，任意簇所用子带被平分给簇内小基站，即每个小基站可利用的频带带宽为 (1-µ)W/3N。最后，为了再次提升用户上行传输性能，宏小区及小小区内MT间的干扰需要被消除。为此，假设任意基站可利用的频带被平分给其所关联的MT。此外，假设每个MEC服务器提供U个具有相同处理能力的计算资源块，其索引集合记为U={1,2,...,U}，其中每个计算资源块的处理能力记为funit。

2.3 通信模型

2.4 计算模型

3 问题建模

显然，问题P2是非凸优化问题，其目标函数和约束表现为混合整数及非线性的形式。

4 算法设计

遗传算法有很强的全局搜索能力，但是局部搜索能力较差[15]；而粒子群算法比较简单，收敛速度很快[16]，但容易陷入局部最优值出现早熟。鉴于两种算法有着互补的优势，因此，类似于文献[4,14]，联合遗传算法和粒子群算法来开发HPSO算法以解决问题P2。为了避免过早收敛，提高收敛速度，糅合了基于DE的自适应遗传算法和自适应粒子群算法，前者用于粗粒度搜索，后者则用于细粒度搜索，算法流程如图2所示。

图2 算法流程图

4.1 遗传算法

作为一种随机搜索算法，遗传算法从一组初始可行解集开始，其关键因素及相应步骤如下：

(1)染色体。在问题P2中，优化参量X被编码成染色体S={sik,∀i ∈I,∀k ∈K}， 参量λ被编码成染色体Q={qik,∀i ∈I,∀k ∈K}， 其中I={1,2,...,I}为个体集群。在任意个体i中，sik和qik分别表示MTk所选择的基站索引号及所获取的计算资源块数，sik=0表示个体i中的MTk不选择基站，在本地完成计算任务。

(2)适应度函数。考虑到约束C1具备混合整数非线性的形式，在遗传算法的初始化和基因操作中难以满足，它被作为一个惩罚项引入适应度函数中。鉴于此，为解决问题P2，个体i的适应度函数被定义为

结合上述遗传算法因素，基于DE的自适应遗传算法的完整过程可概述表1。

表1 基于DE的自适应遗传算法(算法1)

4.2 粒子群算法

在粒子群算法中，粒子(个体)的位置代表问题P2的解，速度则展示解的演化情况。粒子群算法中粒子的初始位置取值为算法1的输出值。具体而言，粒子群算法的关键要素及步骤如下。

结合上述要素，自适应粒子群算法的完整过程可被概述表2。

表3 计算资源块按需分配策略(算法3)

5 仿真及对比分析

5.1 参数设置

在仿真中，本文主要研究了计算资源块和无线信道资源的单位价格对不同卸载算法的任务平均处理时延及任务平均处理成本的影响。通过对比任务的平均处理时延和成本及算法的收敛性来论证所设计算法的有效性。为此，引入如下其他算法作为对照组。

全本地算法：所有MT的计算任务都在本地执行；全关联算法：所有MT的计算任务都卸载到MEC服务器上执行，其中计算资源块分配方式为随机分配。此外，在全关联算法中，本文考虑的是将MT的计算任务卸载到与其对应的信道增益最好的基站上；HGP算法：此算法为文献[4]中分层的遗传和粒子群优化 (Hierarchical Genetic and Particle swarm optimization, HGP)算法，其中计算资源块分配方式为随机分配；HAS算法：此算法为文献[14]中的分层自适应搜索算法，其中计算资源块分配方式为随机分配。

5.2 结果分析

图3给出了两种资源单价的变化对任务平均处理时延的影响。在图3(a)中，无线资源单价ω2固定为1 元/(MHz·s)，在图3(b)中，计算资源块的单价ω3固定为0.1元。可以看到，几种算法下的任务平均处理时延并不会随着计算资源块或无线资源单价的变动而受到影响。这是因为对于在本地计算的任务而言，其处理时延主要取决于任务的数据量和MT的计算能力，而对于要上传到基站进行计算的任务，其处理时延主要取决于传输时的信道状态和分到的计算资源块个数。

此外，在图3中，全本地算法的任务平均处理时延最长，全关联算法最短，其他3种算法则介于两者之间。这是由于其他3种算法考虑了任务截止时延的约束，对于无法在截止时延内完成计算任务的MT，这3种算法才会选择关联基站，而全本地算法中实际存在着不满足时延约束的MT。在全关联算法中，虽然所有任务的时延约束都满足了，但该算法的任务平均处理成本也是最高的。相比于全本地算法，引入资源块按需分配策略的HPSO算法的任务平均处理时延缩短了约25%，资源块随机分配策略下的HAS算法则更低。这是因为这两种算法都满足了时延约束(由图5(b)可验证)，但在随机分配策略下，计算资源块可能存在额外分配的情况。因此，HAS算法下任务平均处理时间会更短，这也意味着HAS算法的开销会更高。

图3 单价变化对任务平均处理时延的影响

图4为两种资源单价的变化对任务平均处理成本的影响。在图4(a)中，随着计算资源块单价的增加，除全本地算法外，其他算法的任务平均处理成本都相应地增加了。虽然全本地算法的任务平均处理成本最低，但是它不能保证所有任务都满足时延约束。随机分配策略下的全关联算法的任务平均处理成本最高，这是因为所有MT都选择将任务上传至基站进行计算，甚至是一些满足时延约束，可以在本地完成计算的任务。另外，可以发现，引入资源块按需分配策略的HPSO算法是使得任务平均处理成本最低的算法。

表4 实验参数

在图4(b)中，引入资源块按需分配策略的HPSO算法依旧是任务处理成本最小的算法。此外，会发现随着无线资源单价的不断提高，HGP算法的任务平均处理成本逐渐逼近甚至高于全关联算法。这是因为随着无线资源单价的提高，传输费用会成为任务处理的主要开销。结合式(10)也不难理解，虽然在全关联算法中或许将一部分可以在本地进行计算的任务上传到了基站，但每次选择的都是对应信道增益最好的基站，而HGP算法由于无法找到一个合适的解(由图5(b)可验证)，最后得到的卸载决策可能并不理想。因此，最终会导致HGP算法下的任务平均处理成本逐渐逼近甚至高于全关联算法。

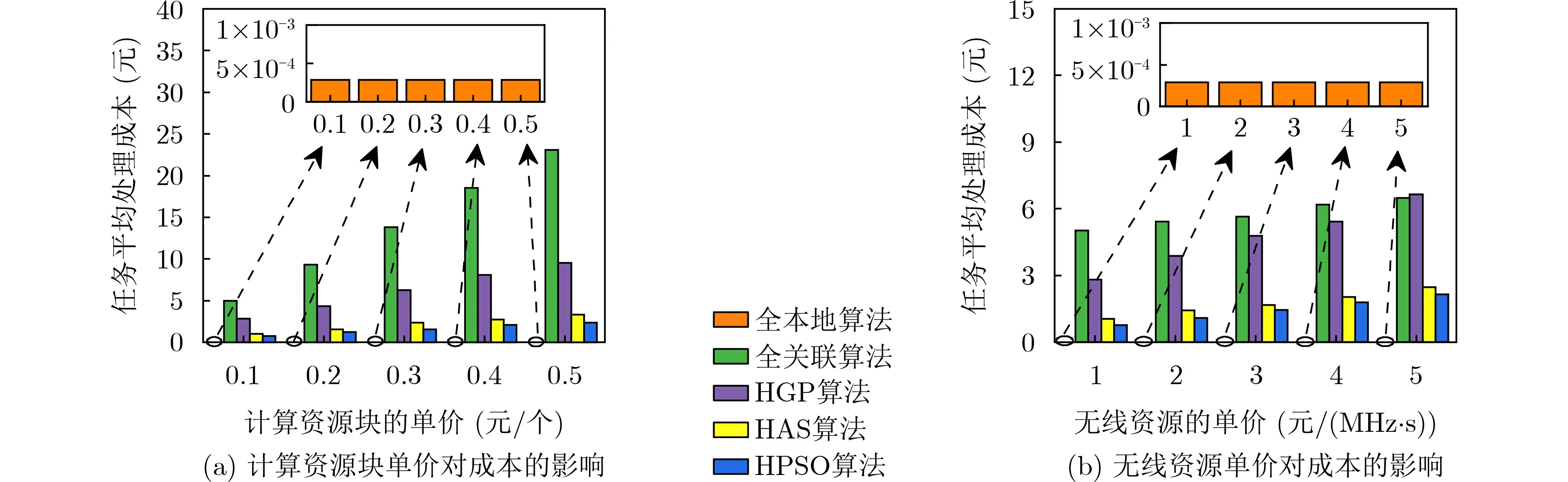
图4 单价变化对任务平均处理成本的影响

图5给出了适应度值在遗传和粒子群算法部分的收敛变化情况。从图5(a)可以发现，在有限的迭代次数内，HGP算法中传统的遗传算法难以求解P2这一混合整数非线性规划问题。而相较于HAS算法中改进的遗传算法，HPSO算法中的自适应遗传算法由于一开始引入计算资源块按需分配策略，使得资源约束条件变得更为苛刻。因此，初始化时最优个体的适应度值较高，但在迭代过程中会快速收敛。

在图5(b)中，HGP算法中传统的粒子群算法在迭代求解过程中依旧没有找到合适的可行解。相比于会对全局最佳粒子的速度和位置进行更新的自适应粒子群算法，HAS算法和HPSO算法中的自适应粒子群算法最终都能收敛。此外，容易发现，采用非线性惯性权重的HPSO算法相比采用线性惯性权重的HAS算法收敛速度明显更快，并且最终的收敛结果更好。

图5 适应度值的搜索情况

6 结束语

本文研究了超密集异构边缘计算网络中任务处理成本最小优化问题。具体而言，在延迟和计算资源约束条件下，联合优化了计算卸载和MEC服务器的计算资源块分配以使用户的任务处理成本降最小。在此之前，一个有效的频带划分方案被引入以用于消除平面间、层间和层内的干扰。考虑到最终所规划的问题具备非线性且混合整数形式，同时为满足问题约束条件及提升算法收敛速度，本文改进HAS以获取HPSO算法。仿真结果表明，同其他卸载算法相比，HPSO算法在减少任务处理成本方面具有显著的优势。