基于自适应光源选择的纠缠光量子定位方法

周 牧 张 靖 谢良波 何 维 李玲霞

(重庆邮电大学通信与信息工程学院 重庆 400065)

1 引言

定位技术广泛应用于国民经济和军事安全的各个方面，为科技进步和社会发展做出了巨大贡献。以全球定位系统(Global Positioning System,GPS)为代表的传统定位系统大多基于牛顿力学[1]、麦克斯韦方程组[2]、香农信息论[3]等经典物理学理论，其定位精度受到经典散粒噪声的限制[4]。然而，量子定位系统(Quantum Positioning System,QPS)利用量子特有的纠缠[5,6]和压缩[7,8]特性，可突破传统定位系统中由信号带宽和功率带来的定位精度限制，达到更高的定位精度[9]。

光量子在自由空间中进行传播时，量子态会不可避免受到大气湍流、雾霾、尘埃和自然环境等不可抗拒因素的影响[10]。2015年，聂敏等人[11]研究了PM 2.5尘埃对量子在自由空间通信信道传输的影响，讨论了PM 2.5尘埃的消光特性与自由空间量子通信信道衰减的关系。仿真结果表明，随着PM 2.5指数和大气湿度的增加，自由空间量子通信的各种性能指标会受到不同程度的影响。2020年，张绣再等人[12]研究了雾的能见度对量子通信信道容量、信道保真度和信道误码率的影响，仿真结果表明，随着雾天能见度的增加，信道容量和信道保真度呈上升趋势，误码率呈下降趋势。同年，中国科学技术大学丛爽等人[13]根据纠缠光在电离层的传播距离误差与电离层自由电子密度和纠缠光频率之间的关系，以及纠缠光在对流层中的传播距离误差与对流层气压、温度等因素之间的关系，提出3种削弱大气干扰影响的量子测距定位方案。通过数值计算，其所提定位方案中定位误差最小可达厘米级。然而，丛爽等人的削弱大气干扰的量子测距定位方案，其定位精度过于依赖设备的精准度，在若干设备中只要有一台设备受到干扰而出现较大的误差，就会导致最终较大的定位误差。

本文考虑到环境对量子定位过程的影响，通过搭建纠缠光量子定位平台，提出基于自适应光源选择的纠缠光量子定位方法，如图1所示。该方法考虑散射环境的动态变化对不同定位光源中传播距离估计性能的影响，首先建立不同散射环境干扰与各光源中信号传播距离之间的数学关系，对各光源信号光时间脉冲序列进行动态分组；其次，对纠缠光时间脉冲序列进行符合计数，根据光的2阶关联曲线得到各光源各分组下的信号传播距离；最后，以各光源各分组下的相对误差为依据，动态选择具有较小相对误差的光源进行定位。

2 算法原理

2.1 数据采集及预处理

2.1.1 纠缠光子对产生

为了保证光束在长距离传输中的质量，需尽可能减小光束的发散角以得到准直光束。因此，信号光经过偏转角为θ的QWP之后，需利用扩束器对光束进行扩束，然后由反射镜发射至目标物体，此时信号光偏振态|φ〉可表示为

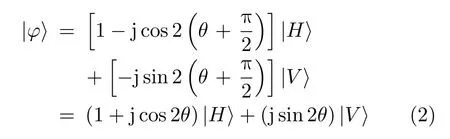
2.1.3 分组设置

2.2 基于符合计数的测距解算

2.2.1 符合计数过程

符合计数[16]可用于测量同时发生或者短时间内发生的关联事件，对于本文而言，由于SPDC过程得到的纠缠光子对时间、偏振和能量高度相关，于是可以利用纠缠光子对间这种天然的关联特性来实现定位。

2.2.2 符合计数值修正

在实际光量子定位过程中，光束可以看成是大量光子的集合，但由于环境中存在各种各样的微粒，使得光子在散射介质中传输时会与散射粒子发生多次碰撞，导致光子的传播路径变长，进而带来符合计数结果误差。为了进一步提升定位精度，该文对散射介质导致的距离误差进行分析，提出散射介质中信号光传播模型，如图2所示。

图2 散射介质中信号光传播模型

2.3 目标位置解算

假设A个光源中单光子探测器探测到的参考光和信号光时间脉冲序列分别为{CH11,CH12,...,CH1A}和{CH21，CH22，...，CH2A}，通过符合计数得到各分组下信号光飞行时间为{τ1,τ2,...,τM}，其中，第m个分组下各光源的信号光飞行时间为τm= (τ1,τ2,...,τA)(m ∈{1,2,...,M})。

对于每个光源，选择最小信号光飞行时间为标准时间τs，计算其他分组下信号光飞行时间与标准时间的相对误差。然后对于每个分组，选取具有较小相对误差的光源vm=(v1,v2,...,vB)用于定位，其中，B为用于定位的光源数。利用筛选出的B个定位光源的信号光飞行时间τm′= (τ1,τ2,...,τB)，计算得到第b个光源信号到目标之间的传播距离lb(b ∈{1,2,...,B})。建立当前分组下选择的光源位置坐标为(xi,yi)与传播距离之间的模型利用最小二乘法即可估计得到目标位置坐标 (x,y)，且随着分组的不同，每次选择不同的光源，实现自适应光源选择定位。

3 算法流程

4 实验结果

我们搭建了纠缠光量子定位平台，实验主要参数如表2所示。本文基于该实验平台得到的实测数据进行仿真验证，具体考虑部署5个光源(如图3所示)，每个光源处数据采集时间为5 s，重复采集50次。

图3 各光源及目标物体位置图

表2 实验主要参数

4.1 不同散射天气下自由程

图4给出了4种不同天气状况对两个不同光源的光子自由程的影响。由图可知，对于单个光源(光源1/光源2)，由于不同天气状况下的消光系数不同，归一化散射自由程均值(即所有散射光子归一化自由程的算术平均)随着天气状况为晴(0.2473/0.1711)、小雨(0.1887/0.1307)、阴(0.1409/0.0976)和雾(0.0359/0.0251)依次变小，其原因为雾天大气中存在大量微小水滴或冰晶组成的悬浮体，使得大气对光子的散射作用变强。对于不同的光源，在相同天气状况下，光源1的归一化散射自由程均值大于光源2，其原因为光子散射自由程除了与天气状况有关，还与光子理想情况下所需走的距离有关。

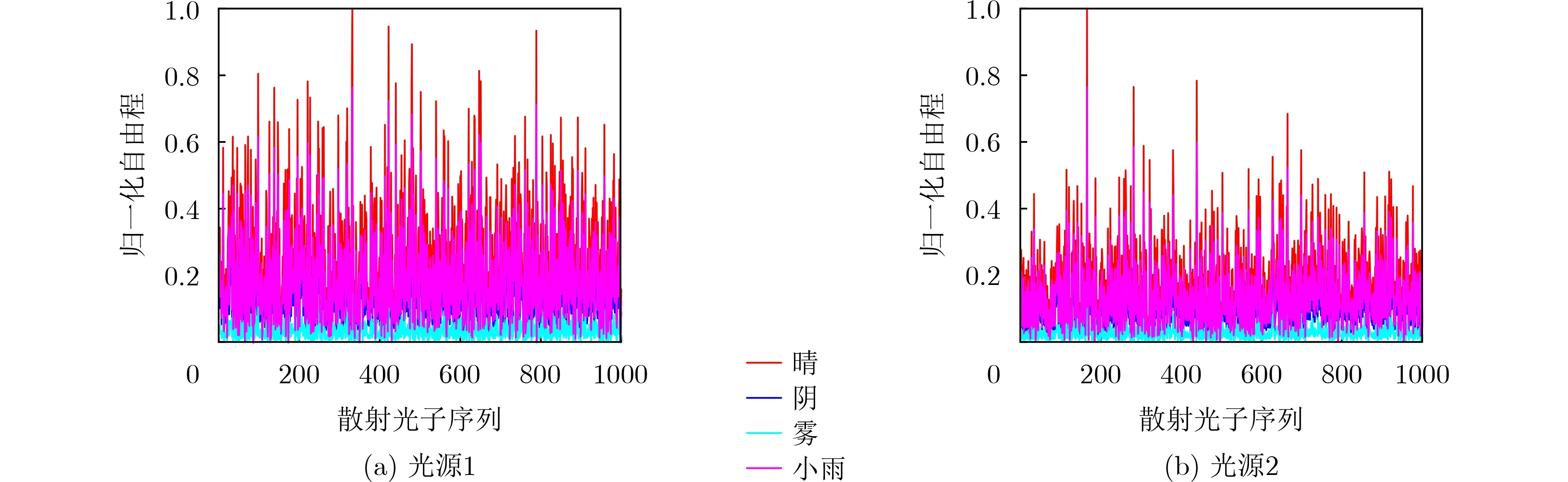
图4 不同天气状况下自由程

4.2 不同分组下符合计数

对于不同光源，图5给出了不同分组下信号光和参考光时间脉冲序列的符合结果。由图可知，对同一个光源来自不同分组的时间脉冲序列做符合计数，其峰值对应的时延值不同，究其原因，在于不同分组下的时间脉冲序列受到环境干扰的程度不同。具体而言，受到环境的干扰越大，符合计数峰值得到的时延值越大，测量误差越大。而对于不同光源，来自同一个分组的时间脉冲序列由于受理想环境下传输距离与环境干扰两方面的影响，导致测量误差不同且各光源测量误差的动态变化。

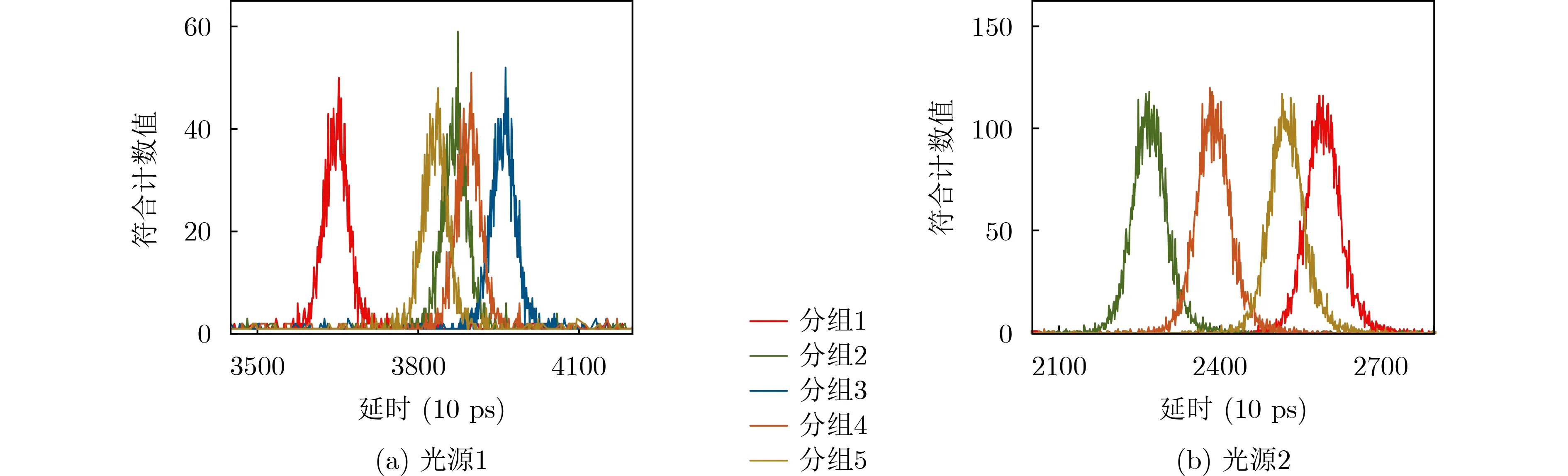
图5 不同分组对符合计数的影响

4.3 不同分组下定位误差

图6给出了光源选择前后不同分组下的定位误差情况，其中，“光源选择后-局部定位”指一直选择特定的光源组合进行定位，“光源选择后-全局定位”指动态选择定位光源组合。具体而言，若当前分组中3个光源的误差较小，且小于前一分组的3个光源误差，则选择当前分组光源进行定位。整体上看，光源选择后的定位误差呈下降趋势，且随着时间的推移(即分组序号变大)，定位误差逐渐收敛。特别地，当累积一段时间后，“光源选择后-全局定位”的定位误差波动明显变小，相较于其他定位方案呈现出较好的鲁棒性。

图6 不同分组下的定位误差

4.4 不同定位光源数下定位误差

图7给出了不同定位光源数对应的定位误差累积分布函数(Cumulative Distribution Function,CDF)。由图可知，在3个、4个和5个定位光源条件下，采用全局定位方式达到0.3m定位误差的置信概率分别为98%，88%和82%，利用不同数量的光源进行全局定位，其定位误差随定位光源数量的增加而增大，其原因为定位光源数量越多，引入大误差的光源的可能性越大，定位误差对环境的变化越敏感。而采用3个定位光源的局部定位方式和未进行光源选择的定位方式达到0.3m定位误差的置信概率仅为30%和16%，远低于本文所提动态选择光源的全局定位方式。

图7 不同定位光源数下CDF

表1 基于自适应光源选择的纠缠光量子定位算法

5 结束语

针对散射环境动态变化而导致纠缠光源定位误差波动大且鲁棒性不高的问题，本文提出了一种基于自适应光源选择的纠缠光量子定位方法。该方法首先利用单光探测器探测到的时间脉冲序列计算光子丢失率，并对时间脉冲序列进行动态分组；然后，基于符合计数方法，通过时间迭代得到各光源各分组下信号传播距离，并以各光源不同分组下的相对误差为依据，选择具有较小误差的光源进行定位。此外，本文通过实验验证了所提方法在较大纠缠光源误差波动情况下不仅可以达到较高的定位精度，且随着时间的累积，本文方法的鲁棒性更好，但定位误差收敛需要一定的时间开销。于是，如何保证较高定位精度同时降低算法的时间开销将成为下一步研究工作。