基于D*Lite算法路径规划的改进方法
2022-09-22戴年慧赵江铭王傲杰胡钡
戴年慧,赵江铭,王傲杰,胡钡
(郑州大学机械与动力工程学院,河南郑州 450001)
0 前言
早在20世纪就开始研究路径规划算法,比如基于图搜索的全局路径规划Dijsktra算法、A*算法[1]、D*算法、Dynamic SWSF-FP等;比如基于采样的全局规划算法PRM算法、RRT算法;比如局部规划算法人工势场法[2]、DWA算法、遗传算法[3]等。
D*Lite算法是在LPA*[4]的基础上提出的一种新的重规划方法。D*Lite算法[5]是一种高效的动态路径规划方法[6]。当然,D*Lite算法也存在着不足,此前有不少人对其进行了改进。随裕猛等[6]进行了D-star Lite算法及其动态路径规划实验研究,使算法在速度上有了较大的提高;张晓冉、居鹤华[7]采用改进D*Lite算法进行自主移动机器人路径规划,引入Bresenham画线算法,并建立分辨率高于全局障碍图的局部障碍图,提高算法对动态环境的适应性;连云霞等[8]将改进D*Lite算法应用在虚拟士兵路径规划中,加入烟花算法减少不必要的转弯,并解决过于靠近障碍物的问题;周燕萍、刘以安[9]研究一种移动机器人的路径规划算法,提出一种结合入侵杂草算法和NURBS算法的混合路径规划方法。在以上基于D*Lite算法的改进方法中,没有针对启发值的改进。另外,余文凯等[10]基于地图预处理及改进A*算法的路径规划,优化子节点的选择,使规划后的路径不再穿过障碍物的顶点,避免机器人与障碍物过于接近甚至碰撞,但由于删除了障碍物周围的危险节点,使得获得路径的概率降低(如终点位于地图角落,其上面节点和右边节点为障碍点时,算法易陷入死循环,而搜索不到一条可行的路径)。
针对以上问题,本文作者提出一种改进方法来提高算法启发值的准确性并优化路径,并通过仿真实验对比,对算法进行验证。
1 D*Lite算法
D*Lite算法是KOENIG S和LIKHACHEV M在LPA*算法的基础上改进并提出的。LPA*算法,即Liflong Planning A*算法,基于A*算法和Dynamic SWSF-FP算法[11]的思想,用来解决动态环境下定起点到定目标点的路径规划问题,采用正向搜索方式。不论是A*算法还是LPA*算法都不适用于车辆(起点)位置变化的情况。基于LPA*算法的D*Lite算法可以很好地应对环境未知的情况,其算法核心是通过最小化rhs值找到目标节点到各个节点的最短距离,所到的节点即设置为起始节点,因此当路径变化和key值需要更新时,更新从目标点到新起始点的启发值和估计成本。
1.1 D*Lite符号说明
D*Lite算法是在Lifelong Planning A*算法的基础上改进的,区别于LPA*算法的部分在于g(s)和rhs(s)的定义,g(s)表示当前节点s到目标节点goal的距离,如下所示:
(1)
(2)
式中:succ(s)∈S,表示节点s∈S的子节点的集合;同样地,pred(s)∈S,表示节点s∈S的父节点的集合,S表示图的节点的有限集。c(s′,s)∈(0,∞)表示从节点s移动到s′∈succ(s)的代价。
起点start∈S到节点s的估计值即为启发值h(start,s),起点start到节点s的距离为两者坐标数值差的最大值。
优先队列U中存放待扩展节点,节点按照key值排序,key定义如式(3)和式(4)所示:
key=[key1,key2]
(3)
其中:
key1=min[g(s),rhs(s)+h(s)]
key2=min[g(s),rhs(s)]
(4)
key中第一个分量直接对应于A*使用的f值,f=g(s)+h(s)。排序规则按照单调非递减目标距离的顺序展开具有相同key值的顶点,例如,key(s1)≤key(s2),表示key1(s1) 局部一致:g(s)=rhs(s)。当所有节点均为一致状态时,即g(s)值等于s到目标点goal的最短距离,可以找到任意一点s到目标点goal的最短路径。比如,当前节点为s,其子节点s′(向着目标点goal前进的小一个节点通过最小的g(s′)+c(s′,s)获得)不断重复直到到达目标点goal。 局部过一致:g(s)>rhs(s)。表示当前节点s可以通过子节点s′使自己到目标点的路径更短,即s′到s的边缘代价函数c(s,s′)值变低,网格上障碍物被清除(c(s,s′)的值从∞变为B)或搜到一条更短的路径。此时,将g(s)设置为rhs(s),节点状态变为局部一致。 局部欠一致:g(s) D*Lite算法流程如图1所示,具体步骤如下: (1)初始化 优先队列U为空集,将所有栅格rhs(s)和g(s)置为无穷大,终点goal的rhs(goal)设置为0,计算终点goal的key值并插入优先队列U中。 (2)计算预设路径 对当前节点的扩展节点计算key值并插入优先队列U中,key值最小的弹出优先队列并作为当前节点,重复这一过程,直到搜索到起始点为止,生成一条可行的路径。 (3)机器人运动 机器人根据预规划的路径运动到下一个点,同时检查环境是否改变。 (4)环境改变 如果环境改变即发现下一个点为障碍点,更新该节点和受影响的节点的参数,回到步骤(2)重新计算路径,直到机器人运动到终点。 前文中介绍的D*Lite算法的改进大多针对算法效率的改进,作者研究了A*算法的启发值和D*Lite算法在预规划路径的表现之后,发现以下一些可以进行改进的地方: (1)启发值对增量式搜索算法很重要。启发值始终是小于或者等于实际路径长度,构造一个较为接近实际长度的启发值对算法性能很有意义。采用一个比切比雪夫距离更接近实际路径长度的启发值。 (2)引入安全系数。采用原始D*Lite算法对路径进行规划可发现斜穿过障碍物栅格的顶点现象。因此,对扩展节点进行分类,对危险节点引入安全系数。 在优先队列U中,根据key的值进行排序。由第1.1节中符号说明中可知,排序取决于第一个分量key1,即(rhs(s)+h(s))(当预规划时),rhs(s)表示当前节点s到目标节点goal的步数。根据A*算法可知,h(s)越精确,扩展次数越少,寻路越快且路径越短;h(s)越小于实际路径,扩展点越多,速度越慢;反之,不能找到最短路径,但是速度很快。一开始使用的距离是切比雪夫距离,如式(5)所示: h(s)=D·max(|sx-startx|,|sy-starty|) (5) 可是这样的启发式不够准确,因为运动中包括斜线运动。所以构造一个更加准确的启发值, dx=|sx-startx| (6) dy=|sy-starty| (7) h(s)=D2·min(dx,dy)+D·(dx+dy-2· min(dx,dy)) (8) 式(8)中:D2表示穿过斜线的代价系数;D表示直穿过的代价系数。第一项表示斜穿过格子的代价值,第二项表示直穿过格子的代价值。对比可知,构造的启发值比式(5)表示的切比雪夫距离更加接近实际的距离。 黑色为障碍物节点,红色为起点,绿色为终点,起点到终点的连线为规划的路径。 优先队列U是closelist扩展的节点的集合,是图中的浅灰色;closelist是优先队列U弹出的节点的集合,是图中的深灰色栅格,表示搜索的次数。由两张图对比可知:图2(a)中closelist中的节点数量为8个,图2(b)中closelist数量为6个,图2(a)比图2(b)多出节点(4,5)和节点(2,2),故而图2(a)的扩展次数比图2(b)的多。由此可知,改进的启发值比切比雪夫距离的启发值更准确,扩展次数减少,性能更好。 D*Lite算法当前节点s的扩展点遵循8个方向进行扩展,如图3所示;当前节点到下一子结点可能会出现碰撞障碍物或者离障碍物过近的现象。针对在这一表现,受文献[10]启发,对子节点加入状态值,降低路径斜穿过障碍物顶点的概率。 图3 父节点与子节点的坐标关系 由图3所示,根据当前父节点与子节点的坐标关系,将父节点周围的子节点进行分类。为了区分子节点,改变危险子节点和已搜索的节点的状态值,具体操作如下: (1)判断危险子节点。如果当前父节点上面的子节点(子节点2)为障碍点,那该子节点的左右两个节点(子节点1、子节点3)标为危险子节点;如果当前父节点右边子节点(子节点4)为障碍点,那么该子节点的上下两个节点(子节点3、子节点5)标为危险子节点;同理推之,当前父节点下面的子节点(子节点6)为障碍点,那么标记该节点的左右两个节点(子节点7、子节点5)为危险子节点;当前父节点左边的子节点(子节点8)为障碍点,标记该节点的上下两个节点(子节点1、子节点7)为危险子节点。 (2)标记危险节点状态值。判断为危险子节点的节点状态值标记为1。 (3)对于状态值state为1的节点,在启发值h中增加一个安全系数cost(oi)。 (4)对于所有搜索过的非危险节点,节点状态值置为-1。 父节点与其扩展子节点的连线到障碍点的距离为D(oi),其代价cost(oi)为 (9) 式(9)中:a表示一个栅格的长度;t表示安全代价值。 由图4可以发现:图4(a)的路径出现了连线斜穿过障碍点的节点,而图4(b)中路径与障碍栅格保持了半个栅格长度的距离,比如,图4(a)中节点(3,4)到节点(2,3)的连线经过障碍点(3,3)的顶点,过于靠近障碍物;在图4(b)中节点(2,3)不作为优先选择,节点(3,4)下一个节点选择了(2,4)。改进后规划的路径没有斜穿过障碍物栅格顶点的现象,而是与障碍物保持了一定距离。 图4 引入安全系数的仿真对比 在MATLAB中进行仿真,分别是5×5、10×10和50×50的栅格,障碍点数量分别是5、14和98,设定障碍点在3种规模的栅格中随机分布,每个网格的大小为一个像素。算法中改变了启发值和加入了安全系数,所以重规划和原算法中重规划原理一样,只不过重规划的路径也体现了预规划路径的性能:扩展节点减少和远离障碍点不是文中的重点,故这里就不做重规划路径的仿真。 由图5可知:改进前的路径都有经过障碍物的顶点,而加入安全系数后规划的路径都与障碍物保持了半个像素的距离。对比文献[10]将危险点都去除的方法,如起始点的上方栅格和右方栅格为障碍点的情况就搜索不到路径,提高了保证路径生成的概率。 图5 三种规模地图的路径规划的仿真对比 表1是3种随机障碍点地图路径规划的结果对比,可知:在搜索次数上,3种规模的地图扩展次数分别减少38.5%、21.4%、50%,;在规划的路径长度上,3种规模的地图路径长度分别增加8.5%、4.7%和减少0.69%。由此可以看出:改进后的算法搜索次数减少,算法搜索效率提高,性能更好;在5×5和10×10的地图中,路径长度是增加的,且长度增加率是减小的;在50×50的地图中,路径长度是减小的,由此可见,该改进算法运用于大地图中的效果更好。 表1 3种规模的栅格路径规划的结果 文章改进了D*Lite算法的启发值,在扩展结点中引入安全系数,对于危险节点将不作为优先选择的节点。通过仿真结果可以看出,改进后的D*Lite算法启发值更精确、更接近实际距离,减少了搜索扩展的次数,并且解决了路径穿过障碍物栅格顶点的问题,提高了算法的搜索效率,能够规划出一条十分安全的路径。1.2 其他概念
1.3 算法流程
2 改进
2.1 构造启发值h
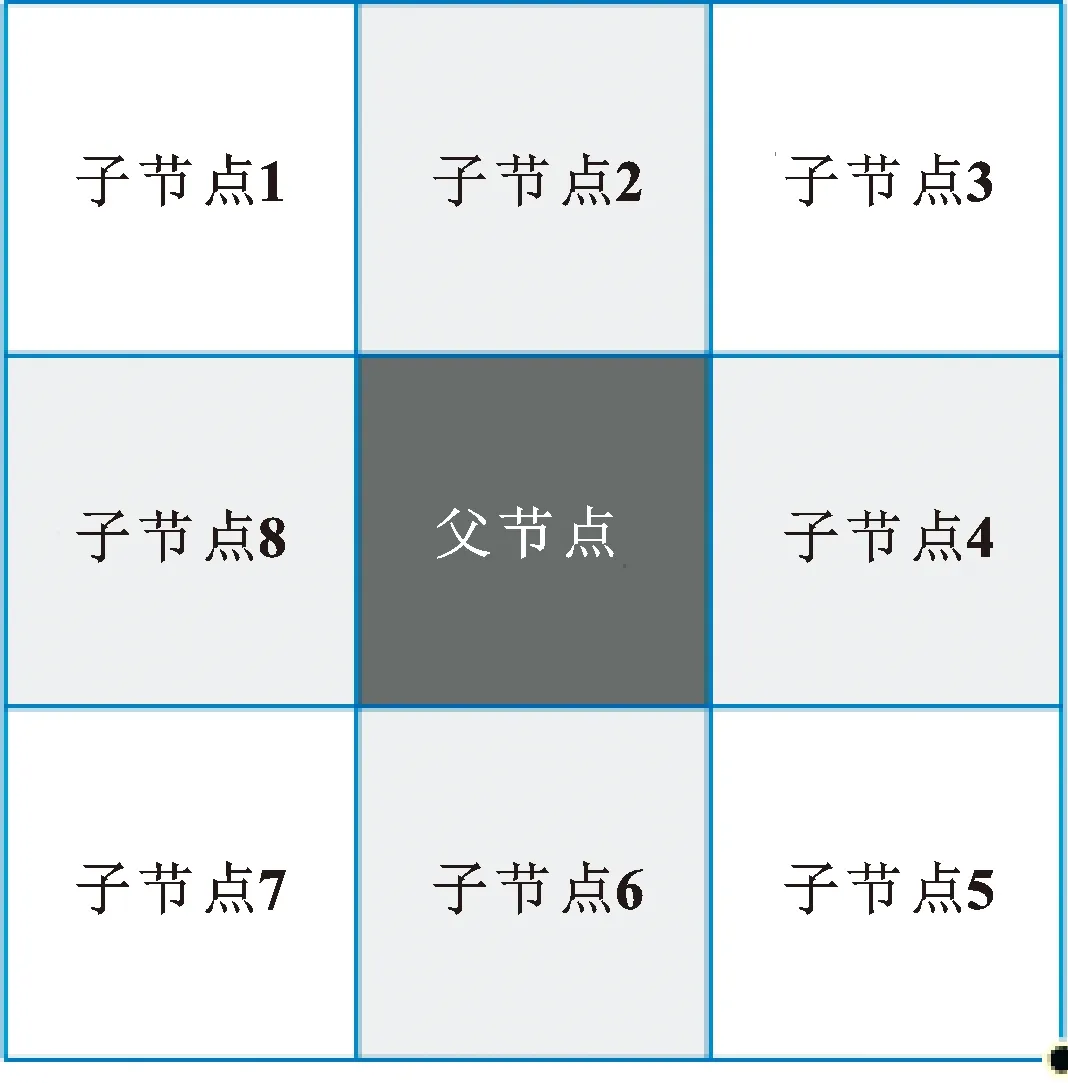
2.2 引入安全系数

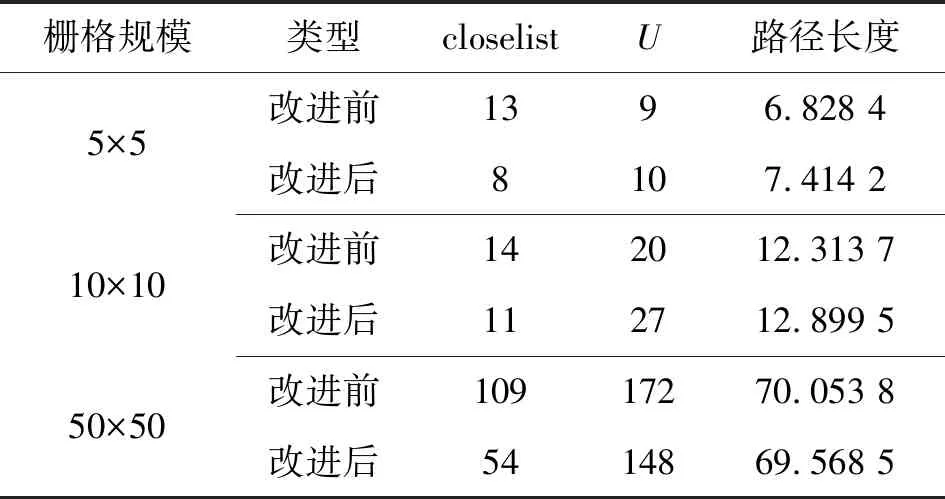
3 仿真结果与分析

4 结论
