机械臂关节空间轨迹的累积非支配赋值NSGA-II算法规划
2022-09-22朱永强鲍官军
朱永强,鲍官军
(1.义乌工商职业技术学院机电信息学院,浙江 义乌 322000;2.浙江工业大学机械工程学院,浙江 杭州 310014)
1 引言
机械臂可以代替人类进行繁重及重复性高的工作,同时减少人身伤害,并提高生产效率和生产质量,因此机械臂在工业生产中得到了越来越广泛的应用,比如装配、焊接、码垛等。机械臂运动轨迹规划是控制技术的核心内容之一,轨迹规划的优劣对机械臂的使用寿命和生产效率影响极大[1]。因此,研究机械臂轨迹规划对提高其使用寿命和生产效率具有重要意义。
按照规划空间的不同,可以将轨迹规划分为关节空间轨迹规划[2]和笛卡尔空间规划[3]。关节空间的轨迹规划是指将关节角表示为时间的函数,其优点是便于设置控制量,缺点是难以对末端执行器进行精确控制。笛卡尔空间轨迹规划是指将末端执行器位姿表示为时间的函数,优点是规划效果直观明了,缺点是运算量、存在奇异性和机械自锁问题。从优化指标的角度讲,机械臂轨迹规划可以分为时间最优[4]、能量最优[5]和冲击最优、多指标优化[6]等。文献[7]针对多个机器人运动路径规划问题,自定了5个交叉变异算子用于改进遗传算法,规划了连续空间中起止点之间的最优路径。文献[8]将改进的模拟退火算法应用于七自由度机械臂的轨迹规划,所规划轨迹具有良好的运行性能。文献[9]以6自由度机械臂为研究对象,将B样条曲线作为机械臂轨迹基元,使用自适应惯性权重约束粒子群算法对轨迹参数进行优化,该方法得到了机械臂的时间最优轨迹,同时克服了运动学奇异性问题。对于机械臂轨迹的规划优劣,不仅与轨迹基元关系较大,而且与优化算法的求解能力关系较大,普遍适用性较强的轨迹规划方法仍然是当前阶段的研究热点。
研究了七自由度冗余机械臂的关节空间轨迹优化问题,建立了关节空间轨迹的多目标优化模型,并将累积非支配赋值的染色体选择法引入到NSGA-II算法中,提高了算法的优化能力,达到了优化机械臂关节空间轨迹的目的。
2 机械臂优化模型
2.1 七自由度冗余机械臂
以7自由度冗余机械臂为研究对象,其实物及D-H 坐标模型,如图1所示。
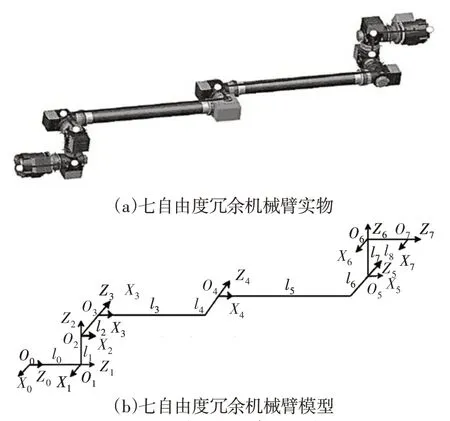
图1 七自由度冗余机械臂Fig.1 7 Degree of Freedom Manipulator
图1(b)中坐标系:x0y0z0—基座坐标系;x1y1z1~x7y7z7—7 个转动关节坐标系。为了防止图片杂乱,图中仅给出了各坐标系的X轴和Z轴,Y轴根据右手定则确定。图中:l0~l8—各连杆尺寸,l0=l8=70cm,l1=l2=l6=l7=43cm,l3=l5=208cm,l4=38.7cm。
2.2 问题描述及建模
研究的是七自由度冗余机械臂在关节空间的轨迹规划问题。根据机械臂的关节活动范围、任务需求和障碍物分布设计其在笛卡尔空间必经的轨迹点,记为P0,P1,P2,…,PM。其中P0为轨迹起点位姿,PM为轨迹终点位姿。
基于机械臂的逆运动学求解方法[10],可以将笛卡尔空间的必经轨迹点转换为关节空间的轨迹点,记为θ0,θ1,θ2,…,θM。对于七自由度机械臂,每个关节空间轨迹点由七个关节角组成,记为θm=(θm1,θm2,…,θm7),式中:m—轨迹点编号。使用插值法设计关节空间必经轨迹点之间的轨迹,通过优化机械臂到达各关节空间轨迹点的时间t0,t1,…,tM,使机械臂在满足约束条件下规划出设定意义下的最优轨迹。优化目标包括工作时间最短、能耗最少和运动冲击最小3个指标。
(1)工作时间最短目标函数。将机械臂到达轨迹点θm的时间记为t0,t1,…,tM,则机械臂的工作时间函数为:

式中:f1—机械臂工作时间。
(2)能耗最少目标函数。根据前文所述,关节n在轨迹点θm对应的关节角为θmn,则机械臂的能耗为:
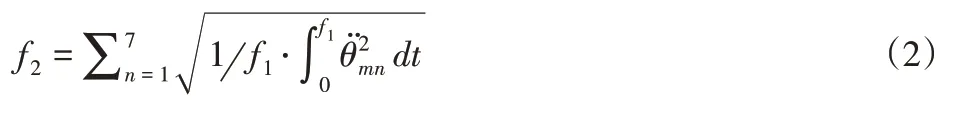
式中:f2—机械臂系统能耗;—第m个轨迹点对应的第n个关节角加速度。
(3)运动冲击最小目标函数。机械臂的运动冲击使用关节角运动的平均加加速度进行衡量,即:
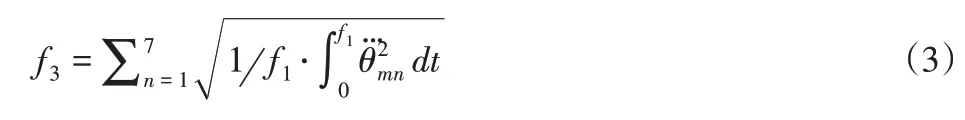
式中:f3—机械臂的运动冲击,—第m个轨迹点对应的第n个关节角加加速度。
机械臂轨迹优化的约束条件包括关节角运动范围约束、关节角速度约束、关节角加速度约束等,即:

式中:θnmax、θnmin—关节n的最大和最小关节角;vnmax—关节n的最大关节角速度;anmax—关节n的最大关节角加速度。
2.3 轨迹插值函数
B样条曲线具有局部支撑性和结构紧密性,当某段局部轨迹不满足约束时只需对此局部轨迹进行改动,其他满足约束的轨迹可不做改变,因此使用B样条曲线作为轨迹插值函数。高于三阶的B样条曲线计算困难且计算量略大,因此在实际应用中使用较少。使用3次B样条曲线作为轨迹插值函数。
3次B样条曲线及其基函数分别为[11]:
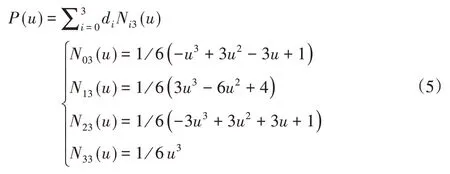
式中:u—(0,1)间参数,P(u)为3次B样条曲线,di(i=0,1,2,3)-控制顶点;Ni3(u)—第i个3次样条基函数。将基函数代入到定义式中,按照参数u的幂次合并同类项,得到3次B样条曲线的多项式形式,为:
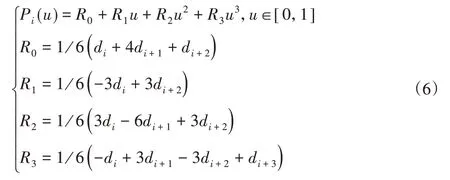
式(6)中的控制顶点di(i=0,1,2,3)由给定的轨迹点和边界约束条件确定,从而得到具体的3次B样条曲线表达式。
3 累积非支配赋值NSGA-II算法优化
3.1 传统NSGA-II算法简介
NSGA-II算法是在遗传算法基础上为适应多目标优化而提出的,主要包括非支配排序、Pareto解集、拥挤度等重要内容[12],在此进行简单介绍和说明,便于后文的算法原理分析。
(1)非支配排序。以N个目标最小化问题为例进行说明,优化目标函数记为fn,n=1,2,…N,若两个染色体x1和x2满足:对∀n∈[1,N],都有fn(x1)≤fn(x2),则称染色体x1支配x2,或者称染色体x2被x1支配。
(2)Pareto解集。将整个染色体种群进行非支配层排序,不被任何个体支配的染色体分配到第1非支配层,将第1非支配层的染色体删除,剩余个体中不受支配的染色体分配到第2非支配层,重复删除和排序的过程,直至所有个体的非支配层排序完毕,一般将第1非支配层个体称为Pareto前沿解集。
(3)拥挤度计算方法。在传统NSGA-II算法中,拥挤度是对同一非支配层的个体定义的。一般将同一非支配层两端染色体的拥挤度定义为无穷大,其余染色体的拥挤度为:

式中:dk—染色体k的拥挤度。
3.2 传统NSGA-II算法缺陷分析
3.2.1 选择策略缺陷分析。
在传统NSGA-II算法中,选择包括两个步骤,首先保留非支配层靠前的染色体,直到保留至某一支配层染色体总数超过设定规模为止,而后在最后选择的非支配层中删除拥挤度靠后的个体使染色体规模保持恒定。
传统NSGA-II算法的选择策略中,拥挤度的计算仅考虑了本非支配层染色体的距离,而没有考虑染色体周围个体的分布密集度,也就是说未考虑染色体被其他个体支配的程度,这显然是不合理的。以图2中的b、c、d三个个体为例进行说明,假设图中a、b、c、d、e为均匀分布。

图2 染色体分布Fig.2 Distribution of Chromosomes
根据非支配层定义,图中染色体I~VI的非支配排序为1,染色体a~e的非支配排序为2。根据拥挤度定义,染色体b、c、d的拥挤度相同,则被保留概率也相同。但是根据图中矩形虚线圈出的个体数量可以看出,染色体d所属范围的密度明显小于染色体c,也同样小于染色体a。这意味着虽然其周围染色体的密集度不同,虽然染色体被支配的程度不同,但是根据传统定义却具有相同的被选概率,这显然是不合理的。
3.2.2 模拟交叉二进制算子缺陷分析。
模拟二进制交叉算子(Simulated Binary Crossover,SBX)可以使子代有选择性地遗传父代的优秀基因,从而保证算法不断向最优解收敛。SBX算子的表达式为:
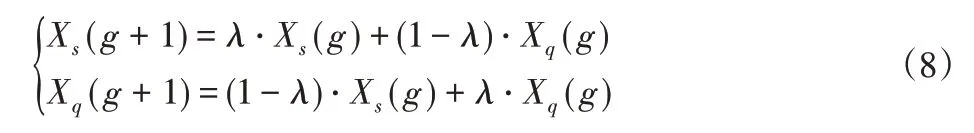
式中:g—迭代次数;Xs(g)—迭代g的染色体s;Xq(g)—迭代g的染色体q;λ—(0,1)间参数。式(8)中参数λ一般依据迭代次数进行设置,但是随着迭代进行,染色体多样性受到破坏,SBX算子的进化能力极为有限,甚至停步不前。
3.3 累积非支配赋值NSGA-II算法
3.3.1 基于累积非支配赋值的选择方法
针对3.2节中分析出的传统NSGA-II算法在选择策略中存在的缺陷,本节提出了累积非支配赋值方法。将染色体的累积非支配赋值定义为所有支配该染色体的个体排序值与该染色体自身排序值之和,即:
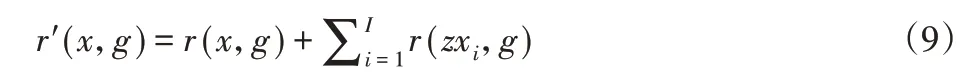
式中:r′(x,g)—染色体x迭代至g代的累积非支配赋值;r(x,g)—染色体x的非支配排序值;I—支配x的染色体数量;zxi—支配x第i个染色体;r(zxi,g)—染色体zxi的非支配排序值。
按照式(9)的定义,染色体b的非支配排序值为2,支配b的染色体为I、II、III、IV,则染色体b 的累积非支配赋值为6。同样地,染色体c的累积非支配赋值为4,染色体d的累积非支配赋值为3,这意味着染色体d周围的密集度低,也意味着能够支配染色体d的个体更少,而能够支配染色体b的个体更多,那么从染色体多样性和特异性角度讲,染色体d应具有更大的选择概率,通过以上定义,可以有效保留染色体多样性和特殊性。
3.3.2 自适应SBX算子
为了保持SBX 算子的进化能力,本节提出了个体自适应λ参数,其思想为:通过个体的累加非支配赋值构造参数λ,使较优的染色体能够更大程度地遗传给子代,方法为:

按照式(9)对累加非支配赋值的定义,个体越优其累加非支配赋值越小。将式(10)代入到式(8)中,个体q越优则λ越小,而(1-λ)越大,个体q越能够将自己的优秀基因遗传给子代。因此通过式(10)的构造,可以使较优个体得到更大程度遗传。
3.4 基于累积非支配赋值NSGA-II算法的优化方法
根据累积非支配赋值NSGA-II算法原理和机械臂关节空间轨迹优化方法,对优化中的具体问题进行明确。
(1)染色体编码。优化对象为各轨迹时间点,则根据轨迹点数量设定染色体的基因位数。将染色体使用十进制编码,基因位数为M,则染色体编码为(t0,t1,…,tM)。
(2)染色体变异方法。根据染色体编码方式和具体问题的限制条件,对染色体使用单点随机变异方法,即随机选择一个基因位,在其取值范围内进行随机变异。
基于累积非支配赋值NSGA-II算法的机械臂关节空间轨迹规划步骤为:
(1)初始化算法参数,即染色体规模、交叉概率、变异概率、最大迭代次数;
(2)染色体按照随机方法进行初始化;
(3)染色体按照概率进行交叉和变异操作;
(4)对染色体进行非支配排序,计算各染色体的累积非支配赋值,依据非支配排序和累积非支配赋值选择染色体;
(5)算法是否达到最大迭代次数,若否则转至(3);若是则输出Pareto前沿解,算法结束。
4 仿真验证
4.1 仿真实验设置
给出图1所示七自由度冗余机械臂关节运动约束条件,七个关节的运动能力完全一致,关节角的活动范围为[-120°,120°],关节角速度的约束范围为[-5°/s,5°/s],关节角加速度的约束范围为[-2°/s2,2°/s2]。根据任务需求、机械臂关节运动约束和障碍物分布情况,得到机械臂在关节空间必须经过的轨迹点,如表1所示。
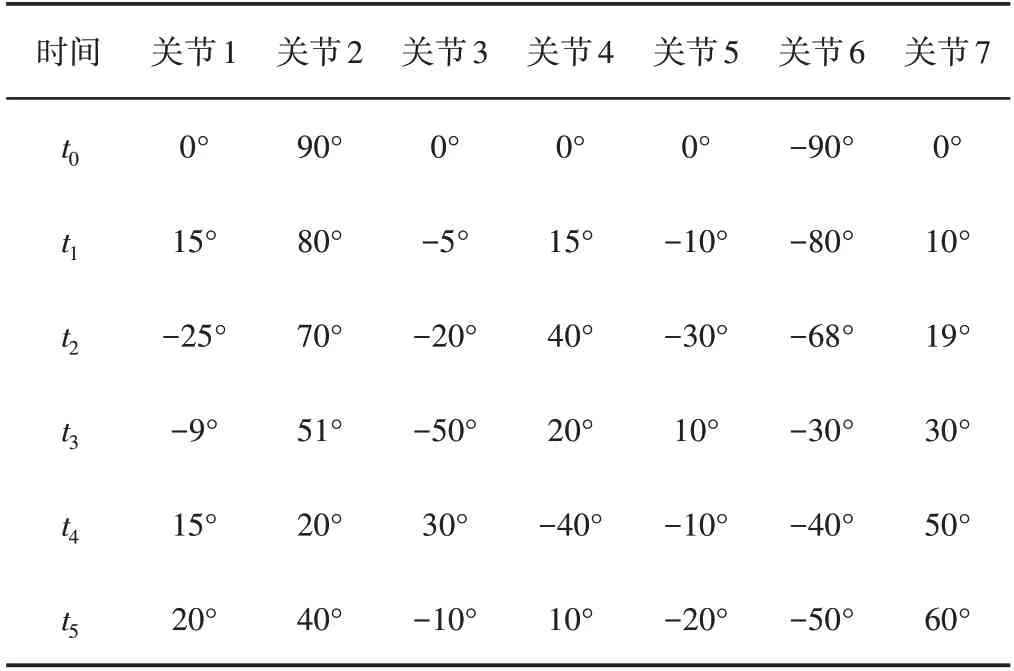
表1 不同算法规划结果统计Tab.1 Statistics of Planning Results of Different Algorithms
4.2 优化结果与分析
算法的参数设置为:染色体规模为250、交叉概率为0.3、变异概率为0.05、最大迭代次数为200。分别使用传统NSGA-II算法和累积非支配赋值NSGA-II算法对4.1节的算例进行优化,得到的Pareto前沿解集,如图3所示。
图3 中实线为传统NSGA-II 算法的优化结果,虚线为累积非支配赋值NSGA-II算法的优化结果。图中A点为能耗和冲击最大点,B 点为能耗和冲击最小点。从Pareto 解集的三维空间分布看,冲击与能耗成正比,这与冲击会增加机械臂能耗的直观理解相吻合。另外,冲击与耗时成反比,能耗也与机械臂耗时成反比,说明一味地提高生产效率而减少生产时间,会较大地增加机械臂耗能。
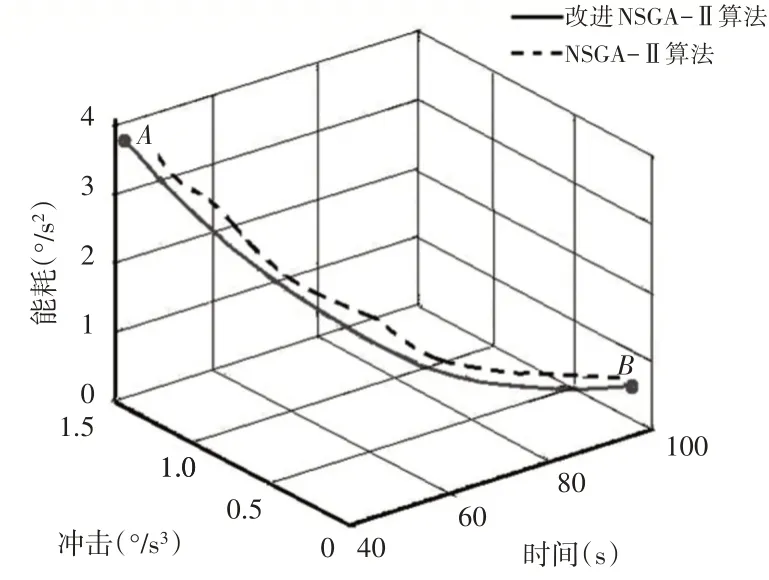
图3 优化的Pareto解集Fig.3 Pareto Solutions after Optimization
考虑到3维空间难以直观比较传统NSGA-II算法与累积非支配赋值NSGA-II算法Pareto解的优劣性,将其在时间-耗能两个维度上进行投影结果,如图4所示。
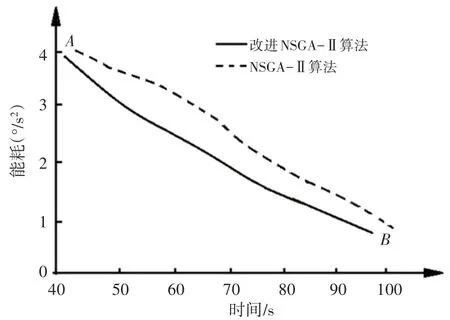
图4 Pareto解集的二维分布Fig.4 2-Dimension Distribution of Pareto Solutions
由图4可以直观看出,累积非支配赋值NSGA-II算法的Pa⁃reto解分布在传统NSGA-II算法的Pareto解左下方,对于多目标最小优化问题来讲,累积非支配赋值NSGA-II算法搜索的Pare⁃to 解集更优。统计图中A点和B点的能耗和耗时,对比结果,如表2所示。
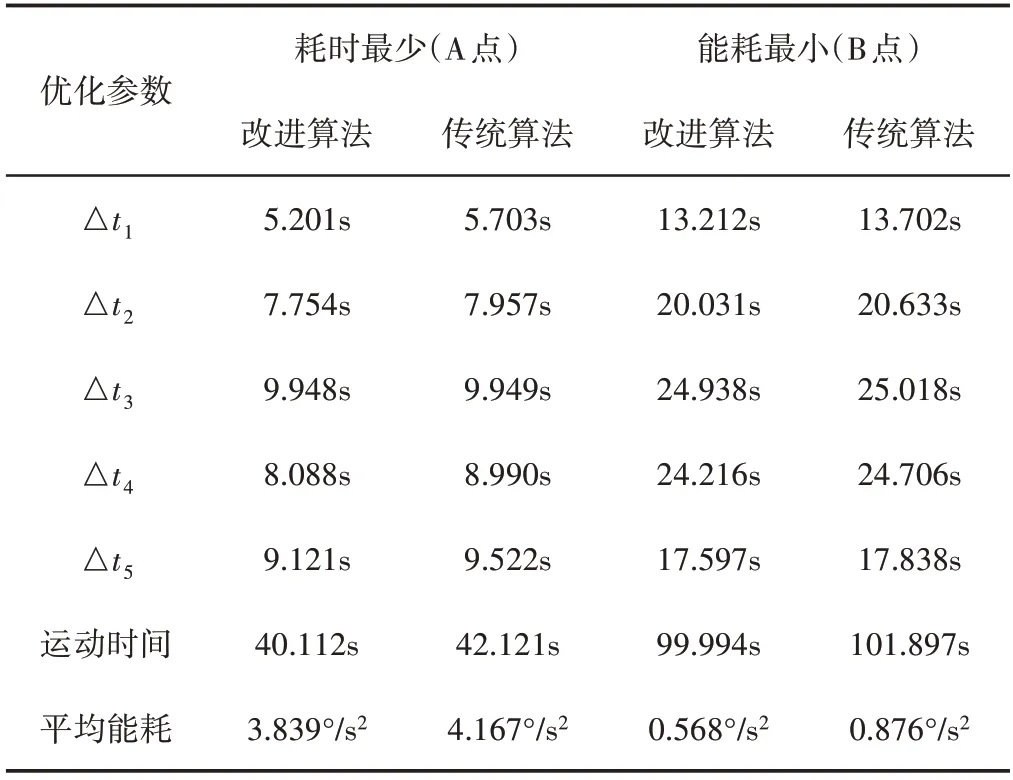
表2 不同算法优化结果对比Tab.2 Optimization Result Comparison of Different Algorithms
由表2中数据可以看出,对于耗时最少点(即A点),传统NS⁃GA-II算法的运动时间为42.121s,能耗为4.167°/s2;改进NSGAII算法的运动时间为40.112s,能耗为3.839°/s2,比传统NSGA-II算法分别减少了4.77%和7.87%。对于能耗最少点(即B点),传统NSGA-II 算法的运动时间为101.879s,能耗为0.876°/s2;改进NSGA-II 算法的运动时间为99.994s,能耗为0.568°/s2,比传统NSGA-II算法分别减少了1.87%和35.16%。结合上述数据和图4可以看出,累积非支配赋值NSGA-II算法的搜索结果优于传统NSGA-II算法,这是因为在累积非支配赋值NSGA-II算法中引入的累积非支配赋值排序法,充分考虑了染色体周围个体的密集度及自身的特殊性,进化过程中可以较好的保留染色体的多样性,因此改进NSGA-II算法的优化结果优于传累积非支配赋值NS⁃GA-II算法统算法。以累积非支配赋值NSGA-II算法搜索的时间最少结果为例,给出7个机械臂的关节轨迹,如图5所示。
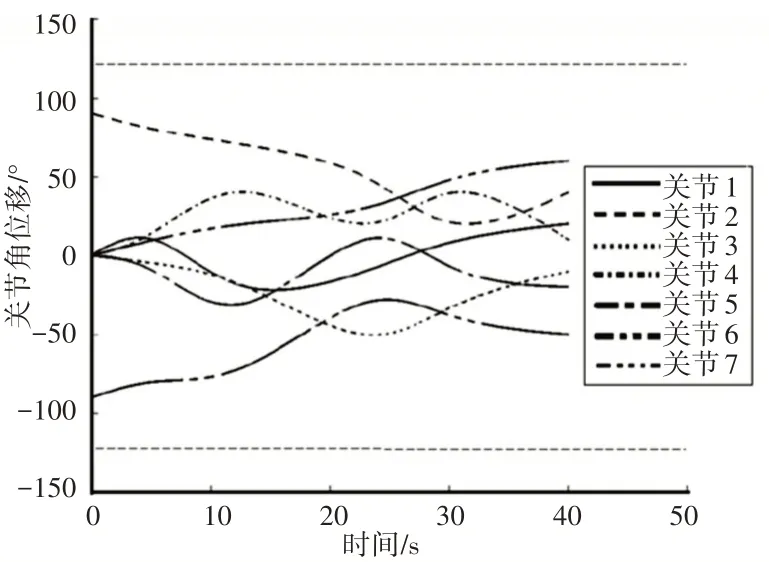
图5 耗时最少轨迹Fig.5 Trajectory of Minimizing Time-cost
经计算和统计,图5给定的耗时最少轨迹,其关节角度运动范围、关节角速度、关节角加速度均满足设定的约束条件,可以实际运行。且机械臂某些关节速度和加速度达到了约束最大值,说明约束空间得到了充分利用。
5 结论
这里研究了七自由度冗余机械臂的关节空间多目标优化问题,建立了多目标优化模型,使用NSGA-II算法进行了多目标优化,经验证可以得出以下结论:(1)累积非支配赋值的选择方法可以更好地保护染色体多样性,从而提高算法的优化能力;(2)基于累积非支配赋值NSGA-II算法优化的轨迹满足约束条件,且优于传统NSGA-II算法的优化结果。
