超声纵振枪式气钻结构设计及仿真研究
2022-09-22高延峰
杨 兴,高延峰
(南昌航空大学航空制造工程学院,江西 南昌 330063)
1 引言
碳纤维增强树脂基复合材料(Carbon Fiber Reinforced Plas⁃tics,CFRP)因其强度高、密度小、生产简单等特点,被广泛用于飞机的结构件制作,并通过螺栓和其他构件进行装配[1-2]。因此,在飞机上装配现场不可避免的需要钻削大量连接孔。
为提高装配效率和适应现场的灵活性,通常使用枪式气钻来加工连接孔。对于碳纤维复合材料这种难加工材料[3],想要获得高质量连接孔十分困难[4]。传统的枪式气钻在钻孔过程中容易出现纤维撕裂分层、树脂材料烧伤、出口毛刺等缺陷[5]。
所以,枪式气钻加工高质量的连接孔是航空航天领域迫切需要解决的问题。
超声振动加工的原理是给刀具或者工件施加微米级超声频率的振动,并通过控制其振动频率、振动幅度及振动方向,使加工工具和工件之间产生周期性的高频分离,从而大幅改善材料的可加工性[6]。文献[7-8]通过研究发现采用高频小振幅的超声辅助套孔加工能够有效的降低复合材料出口分层的缺陷。
文献[9]设计了一种应用在铣床上的超声振动钻削装置,该装置在碳纤维复合材料和钛合金的钻孔试验中能够大幅度的降低钻削过程中的轴向力。然而传统的超声加工设备结构复杂、体积大,都是应用于机床或者加工中心上,此类超声设备的便携性较差,限制了超声振动在风动工具中的应用,无法应用于飞机蒙皮装配现场中的手工钻孔当中。
针对目前超声加工设备难以轻量化的问题,利用传统解析法理论,设计了一套能够应用于枪式气钻的超声换能器,利用Pz⁃Flex软件对超声换能器进行有限元仿真分析。通过理论设计,制作出超声换能器实物,并对其进行谐振频率测试和振幅测试。
2 超声纵振枪式气钻结构设计
2.1 整体结构设计
该超声振动钻孔装置主要由超声换能器、枪式气钻、碳刷、集电环等组成,具体结构,如图1所示。
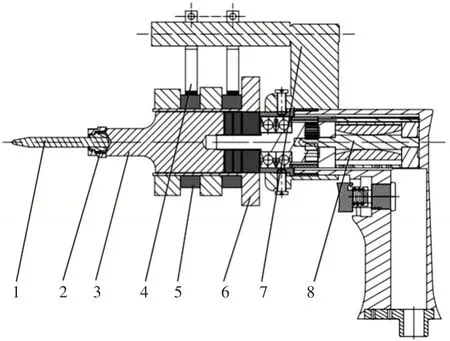
图1 超声振动钻孔装置结构Fig.1 Structure Drawing of Ultrasonic Vibration Drilling Device
该装置采用带工具头的超声换能器代替传统的气钻夹头,气枪旋转主轴与超声换能器连接,通过碳刷及导电铜环对超声换能器进行供电,使得钻头在加工过程中能产生一个垂直于工件表面的高频超声振动。
2.2 换能器设计理论
把装配好的超声换能器当做一个整体,假设其为一连续的弹性体,在变截面杆上可应用一维纵振波动理论求解,如图2所示。
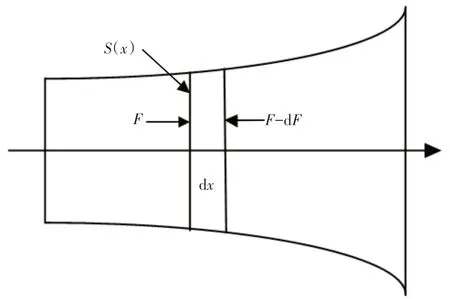
图2 变截面杆的振动原理Fig.2 Principle of Vibration of Bar with Variable Section
根据胡克定律:

和牛顿第二定律:

可得变截面杆的一维波动方程为:
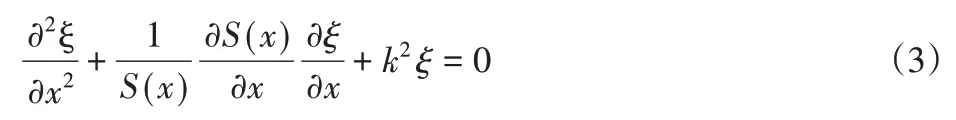
式中:T—应力;F—弹性力;
S(x)—轴上任一位置x处的横截面积;
Y—变截面杆的杨氏模量;
∂ξ/∂x—变截面杆在x处的应变;
ξ(x)—质点的位移函数;且k=ω/c=2πf/c;
f—振动频率;
c—材料中的纵波声速。
将换能器看出均匀等截面杆,因S(x)为常数,故∂S(x)/∂x=0;物体的振动速度v=jωξ,所以超声换能器各部分的振速方程为:

振速方程通解为:
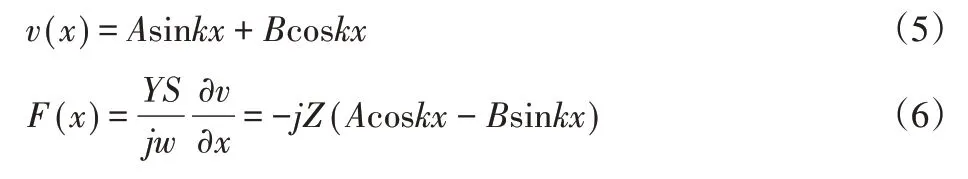
式中:v—质点振速;
Z—超声换能器各部分的声阻抗特性,Z=ρcS;
ρ—材料密度;
c—材料纵波声速;
S—横截面积;
A、B—待定系数。
2.3 换能器设计
目前广泛采用的超声换能器主要有磁致伸缩换能器和夹心式压电换能器,由于夹心式换能器具有制造容易、结构简单、能量转换效率高的优点,因此可采用夹心式换能器结构。
为了减少能量损耗,将前盖板与变幅杆做成一个整体,并统称为变幅杆。换能器上有一个特殊的截面,称之为节面,节面上的任一点的在简谐振动过程中的位移始终为零。设计变幅杆时,可将节面设置在变幅杆与陶瓷堆之间的交界面,超声换能器模型,如图3所示。
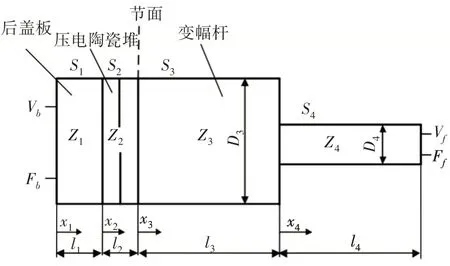
图3 超声换能器模型Fig.3 Ultrasonic Transducer Model
材料的密度、纵波声速、声阻抗特性、横截面积、直径和各元件的长度分别用ρ、v、Z、S、D和l表示;变幅杆大端的直径与压电陶瓷片和后盖板直径相等;前、后表面的振速、应力分别用vf、Ff和vb、Fb表示,由于后表面暴露在空气中,所以Fb=0。
节面左侧是换能器的后盖板和压电陶瓷堆,根据应力和振速应连续传递原理,可得节面左侧的边界条件为:
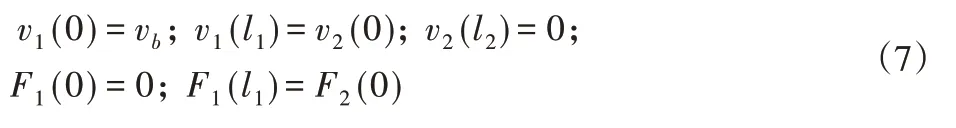
将振动方程的通解式(5)和式(6)代入边界条件式(7)中可得换能器左侧的频率方程为:

节面右侧为换能器的变幅杆,变幅杆主要起到聚能和振幅放大的作用,同理可得右侧的边界条件为:
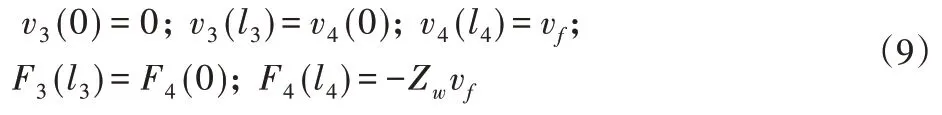
式中:Zw—小端面的输入阻抗,在换能器的设计中该值一般根据经验数据取为零,因此式(5)中的F4(l4)=0。
将振动方程的通解式(5)和式(6)代入边界条件式9中可得出换能器右侧的频率方程为:

2.4 换能器材料及尺寸的确定
在夹心式压电换能器中,压电陶瓷的作用是将电能转换成机械能。常用的压电陶瓷材料有PZT-4、PZT-5、PZT-8等,综合考虑下选择机械品质因素较高的PZT-8,压电陶瓷片外径为35mm,内径为15mm,厚度为5 mm,数量为2片。
变幅杆在工作过程中一直处于高频振动状态,因此变幅杆材料选用机械性能较好的45钢,该45钢需要进行调质处理,以降低其损耗系数。后盖板的作用主要是保证能量尽量向前传输,尽可能的减少从后面传输,一般选用45钢或者钛合金,这里同样采用45钢。设定换能器的工作频率为34kHz,换能器所用材料的基本参数,如表1所示。

表1 超声换能器各组成部件材料参数Tab.1 Material Parameters of Components of Ultrasonic Transducer
压电陶瓷堆的长度l2为两片压电陶瓷片和两片电极片长度总和,电极片厚度为0.1mm,故l2=10.2mm,后盖板直径与压电陶瓷片直径相等即D1=D2=35mm,根据表1中材料参数和左侧的频率方程式(8)可求出后盖板长度l1=12.6mm。
变幅杆大端直径与压电陶瓷片直径相等,D3=D2=35mm;变幅杆小端要与ER11A的夹紧螺母配套,故变幅杆小端的直径D4取为14mm;大小端长度取相等的情况,即l3=l4,根据表1中材料参数和右侧的频率方程式(10)可以求出变幅杆大小端长度为l3=l4=38.9mm。阶梯变幅杆在截面突变处有很大的应力集中,在细部接近突变处容易发生因疲劳而断裂的现象,所以一般将突变处做成有过渡圆弧的形式[10],过渡圆弧半径尺寸计算过程如下:
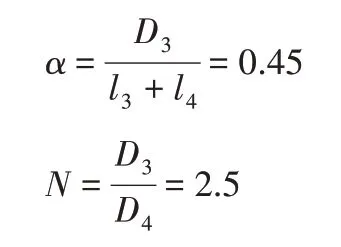
由α及面积系数N可知过渡圆弧半径R与变幅杆小端直径的比值为R/D4=0.625[10],故过渡圆弧半径R=8.75mm。换能器各部件尺寸,如图4所示。
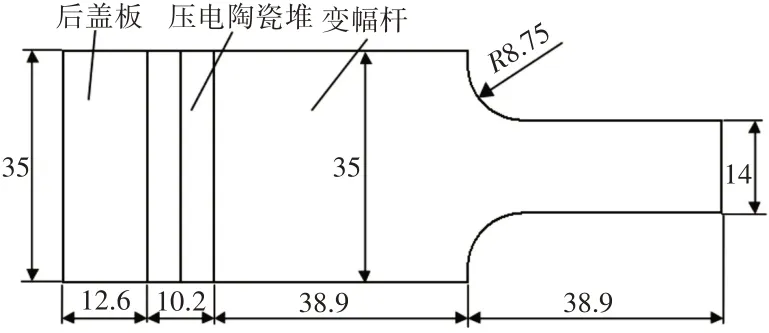
图4 超声换能器各部件尺寸Fig.4 Dimensions of Ultrasonic Transducer Components
3 超声换能器有限元仿真分析
3.1 PzFlex介绍
PzFlex 是专为压电和超声应用而开发的波传播软件,主要用于解决压电换能和超声波传播方面的问题。PzFlex采用混合求解的方法,后盖板、变幅杆采用瞬态动力学方程求解;而对于PZT单元,则利用压电方程来描述其力电耦合特性。
超声换能器的瞬态动力学方程式为:
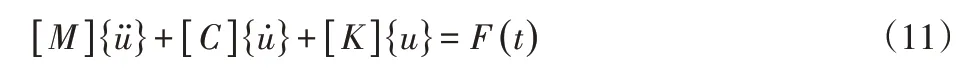
式中:M、C、K、μ、F—质量、阻尼系数弹性系数、位移、载荷。PZT单元的压电方程式为:

式中:T、S、CD、h、D—应力、应变电场强度、弹性系数、压电系数和电位移。
3.2 超声换能器仿真分析
3.2.1 求解过程
模型建立:根据理论计算的结果绘制超声换能器的三维模型,并将三维模型导入PzFlex中。
材料定义:三维模型导入后需对各部件赋予相应的材料参数,通过PzFlex材料编辑模块给换能器各部件赋予材料属性,由于压电陶瓷为各向异性材料,因此需要将陶瓷片厚度方向(Z轴方向)指定为压电陶瓷的极化方向。
网格划分:PzFlex在划分网格时,只需在网格器中输入满足需求的频率以及单个波长划分的网格数目,网格器就会自动计算所需网格单元的大小和数量。在保证效率和精度的条件下设置每个波长为15个网格单元,网格划分后的模型,如图5所示。
图5 超声换能器的网格单元模型Fig.5 Grid Element Model of Ultrasonic Transducer
边界条件:超声换能器在实际工作中受负载作用影响较小,因此可将超声换能器的边界条件设置为自由状态。
载荷施加:创建的仿真模型中包含有压电陶瓷片和电极片,为了使得压电陶瓷片产生超声振动,需要给模型两片压电陶瓷中间的正极加载一个频率为100kHz、幅值为1的激励源,压电陶瓷两端的负极接地置零。
3.2.2 仿真结果
给超声换能器正负极施加超声激励源可得到Z轴方向上的时域位移曲线,通过FFT(快速傅里叶变换)处理器对时域位移曲线进行傅里叶变换,可获得多阶谐振频率的幅频特性曲线,如图6所示。
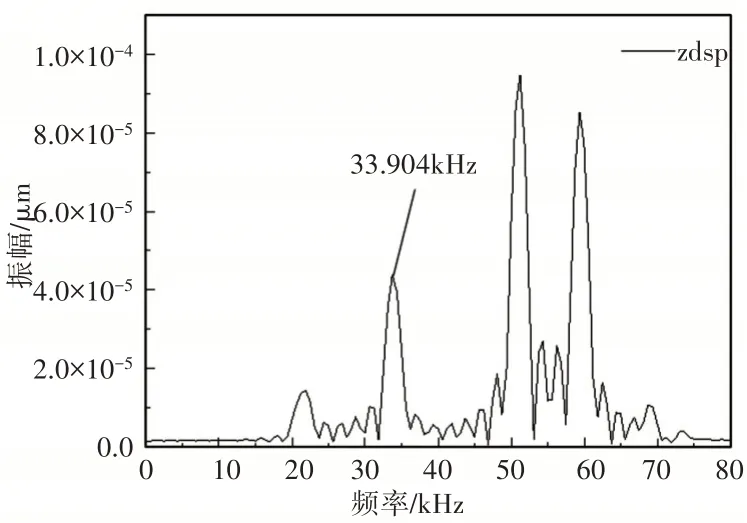
图6 多阶幅频特性曲线Fig.6 Multi-Order Amplitude-Frequency Characteristic Curve
经过处理后得到的多阶幅频特性曲线,表明该超声换能器仿真模型存在多个谐振点。理论设计频率为34kHz,取与其最接近的谐振点即第二个谐振点,第二个谐振点的谐振频率为33.904kHz,与设计值34kHz误差率为0.96%,在误差允许范围内。在二阶谐振频率(33.904kHz)下给超声换能器的正负极施加电压140V、周期无限的电压激励,可得到超声换能器输出端的Z轴方向的时域位移曲线,如图7所示。
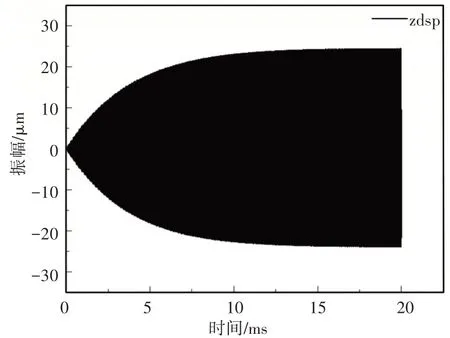
图7 超声换能器Z方向上的时域位移曲线Fig.7 Time-Domain Displacement Curve of Ultrasonic Transducer in Z Direction
从图中可以看出超声换能器的输出端的振幅由0慢慢增大,最后趋于稳定状态,达到稳定状态时的振幅为23.5μm,说明该换能器的振动幅值稳定,能产生周期性的高频振动。
通过后处理模块可以得到二阶谐振频率下的位移云图,如图8所示。从位移云图中可以看出位移主要变形集中在换能器输出端的刀具上,且换能器其他部位的零件没有发生变形,说明换能器结构良好并且能够产生稳定的周期振动。

图8 超声换能器Z方向位移云图Fig.8 Z-Direction Displacement Cloud Image of Ultrasonic Transducer
3.3 整体结构有限元分析过程
3.3.1 求解过程
模型建立:由于超声换能器是安装在枪式气钻上进行工作的,因此需对装配在枪式气钻上的超声换能器整体结构(下称整体结构)进行有限元仿真分析。构建好枪式气钻的三维模型后,将超声换能器装配并将三维模型导入PzFlex中。
材料定义:该整体结构中超声换能器部分的材料属性与前文一致,枪体材料采用铝合金,枪体内部的零件在材料分配时可赋于空属性。
网格划分:装配了超声换能器的整体模型尺寸较大,若网格划分太过于精确,则会耗费大量的时间。在保证效率和精度的条件下将网格数量划分为(500~600)万个单元,如图9所示。
图9 整体结构的网格单元模型Fig.9 Grid Element Model of the Whole Structure
边界条件、载荷施加与前文一致,这里不重复赘述。
3.3.2 仿真结果
给整体结构中的超声换能器正负极施加一个频率为100kHz、幅值为1 的激励源后可得到Z轴方向上的时域位移曲线。时域位移曲线经FFT处理器处理后可得到多阶幅频特性曲线,如图10所示。
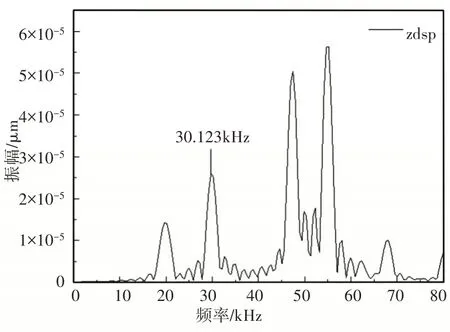
图10 多阶幅频特性曲线Fig.10 Multi-Order Amplitude-Frequency Characteristic Curve
取与理论设计频率最接近的谐振点,从图中可知第二个谐振点的谐振频率为30.123kHz,故整体结构的谐振频率为30.123kHz。
在二阶谐振频率(30.123kHz)下对超声换能器的正负极施加电压140V、周期无限的电压激励,可得到超声换能器输出端的Z方向的时域位移图,如图11所示。
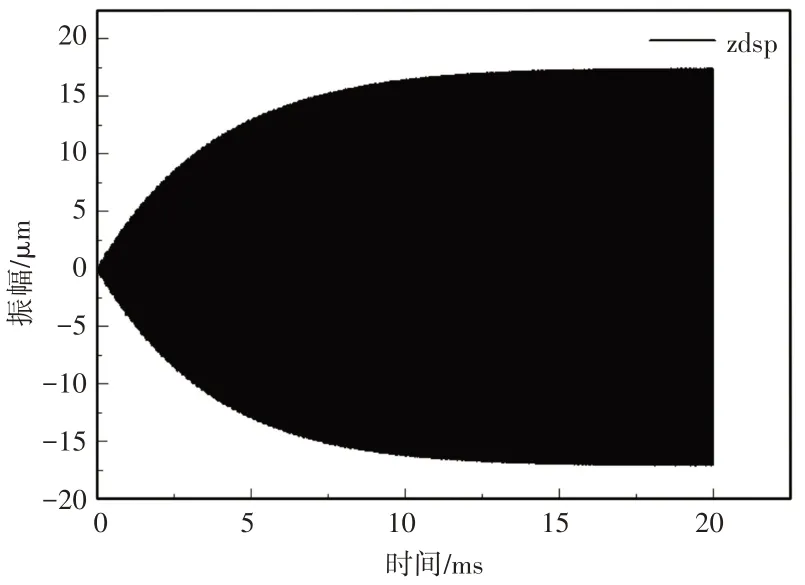
图11 整体结构在Z方向上的时域位移曲线Fig.11 Time-Domain Displacement Curve of the Overall Structure in the Z Direction
该曲线达到稳态后的振幅为15.4μm,说明装配有超声换能器的枪式气钻仍能产生稳定的周期振动。通过对时域位移曲线进行后处理可以得到二阶谐振频率下的位移云图,如图12所示。
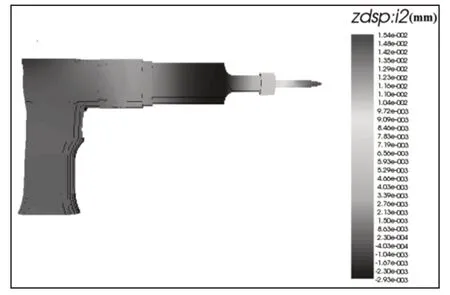
图12 整体结构在Z方向上的位移云图Fig.12 Displacement Cloud Image of the Overall Structure in the Z Direction
从位移云图中可知该结构的变形主要集中在刀尖上,变形良好,该超声换能器可以和枪式气钻进行较好的频率匹配。
4 超声换能器测试
在完成超声纵振换能器的设计,确定个部件的尺寸后对超声换能器进行加工装配,最终得到超声换能器实物,如图13所示。

图13 超声换能器实物Fig.13 Ultrasonic Transducer
将该换能器及其他零件装配在枪式气钻上后得到的超声振动钻孔装置实物,如图14所示。

图14 超声纵振枪式气钻实物Fig.14 Ultrasonic Longitudinal Vibration Pneumatic Gun Drilll
装置采用ER11A的夹头,可装夹φ≤6mm的刀具。为了验证及优化该装置,需要对其进行性能测试。
4.1 谐振频率测试
利用日本恩乃普公司FRA5022型频率特性分析仪对超声换能器进行频率特性分析。设置频率特性分析仪频率扫描范围为(10~60)kHz,自上而下对被测元件进行扫频分析。换能器谐振频率测试结果,如表2所示。

表2 超声换能器谐振频率测试结果Tab.2 Test Results of Resonance Frequency of Ultrasonic Transducer
由表2 可知,超声换能器谐振频率实际测量值比仿真值略小,且仿真值与理论设计值相比又有所降低;而整体结构的谐振频率实际测量值比仿真值偏大。实际测试结果与仿真结果存在差异,是因为有限元仿真过程是理想化模型,忽略了实际使用的材料参数对换能器谐振频率的影响;换能器加工过程中精度达不到理论设计要求;实际换能器组装中装配带来的误差;整体结构仿真分析中的模型是理想化的模型,忽略了气钻内部零件对仿真的影响。
4.2 振幅测试
利用恩乃普公司的W1974 型信号发生器和HSA4052 型功率放大器、宝利泰NLV-2500 型多普勒激光测振仪来对超声换能器的振幅进行测量。根据超声换能器及整体的有限元分析结果,基于超声换能器的实际谐振频率,在140V 电压的激励下对换能器输出端进行振幅测试。超声换能器振幅测量现场,如图15所示。

图15 能器振幅测量现场Fig.15 Ultrasonic Transducer Amplitude Measurement Site
经测试超声换能器的振幅,如图16所示。从图中可知换能器纵向振幅为3μm,幅值稳定。
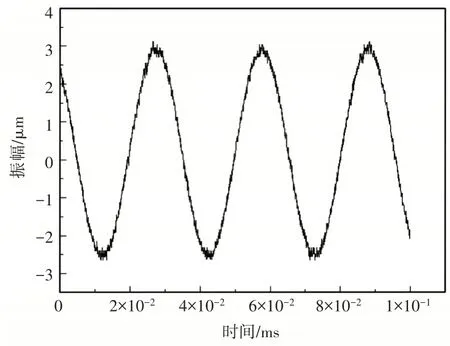
图16 超声换能器振幅Fig.16 Ultrasonic Transducer Amplitude
采用同样的方法对整体结构进行振幅测试,在140V 电压下进行多次实验,测得整体结构的振幅输出,如图17 所示。从图中可知将超声换能器装配到枪式气钻上后,振动幅值减小,说明装配了枪式气钻后的超声换能器振动能量有较大的损耗。
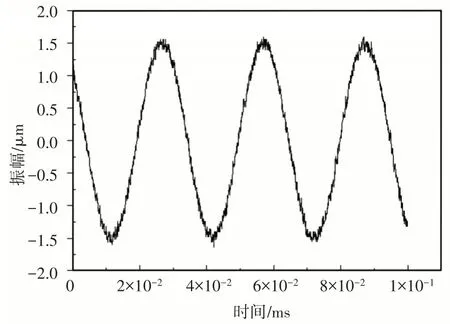
图17 整体结构振幅Fig.17 Overall Structural Amplitude
实验测得超声换能器振幅在140V 电压激励下的振幅为3μm,整体振幅为1.5μm,这与仿真结果23.5μm和15.4μm存在较大的差异,造成差异的原因有:
仿真分析中的材料是理想且均匀的,而实验所采用的材料或多或少的存在各种缺陷;仿真过程中换能器各部件的端面耦合是理想的、完全的,而在实际装配过程中,尽管对换能器各部件的接触面进行抛光处理,但是仍存在缺陷。该超声振动幅值能够满足正常的钻削加工,可以得出设计的超声振动钻削装置符合要求,可以应用于超声钻削。
5 结论
针对传统枪式气钻钻削碳纤维复合材料时容易出现分层、毛刺、撕裂的问题,利用传统解析法理论设计了一种可应用于枪式气钻的超声换能器。通过PzFlex软件对超声换能器和枪式气钻整体进行了仿真分析,并对其进行试验验证,得到以下结论:
(1)超声换能器通过有限元仿真求得的谐振频率为33.904kHz,实际谐振频率为33.019kHz,误差率为2.680%,超声换能器结构设计合理。
(2)超声换能器装配枪式气钻上测得的实际谐振频率为32.427kHz,仿真计算得到的谐振频率为30.123kHz,误差率为7.619%,该换能器结构能够和枪式气钻进行较好的匹配。
(3)通过对超声换能器和整体结构的振幅进行分析测试,表明该超声换能器的振幅为3μm,整体振幅为1.5μm,所设计的超声振动枪式气钻产生的振幅能满足钻削加工。
