机械臂时间最优轨迹的样条曲线拟合与智能规划
2022-09-22袁旭华林喜辉
袁旭华,刘 羽,林喜辉
(1.延安大学数学与计算机科学学院,陕西 延安 716000;2.延安大学石油工程与环境工程学院,陕西 延安 716000;3.北海职业学院,广西 北海 536000)
1 引言
机械臂控制律是在关节空间中设计的,机械臂关节空间轨迹规划是机械臂控制的基础。合理的工作轨迹不仅能够提高工作效率、降低能耗,而且影响产品质量和工作安全[1],因此研究机械臂在关节空间轨迹规划问题具有安全意义和经济意义。
按照研究空间的不同,机械臂轨迹规划分为笛卡尔空间规划和关节空间规划,笛卡尔空间规划是针对机械臂末端执行器的轨迹规划,存在奇异解问题和可控性不强的问题[2],对笛卡尔空间轨迹的跟踪一般需要首先转化到关节空间中。关节空间轨迹规划是通过规划每个关节角的轨迹,使末端执行器能够通过某些特定位置而后到达目标位置,关节空间轨迹的可控性极强,但是难以对笛卡尔空间完全跟踪,只能通过设定的若干位置[3]。就轨迹规划的目标而言,可以分为时间最优、能量消耗最优、冲击最小及三者组成的综合目标[4-5],其中以时间最优研究最多,这是因为时间最优代表着生产效率最高,生产效率高带来的经济效益必然抵消了机械臂能耗成本,因此时间最优轨迹规划更具有研究价值。文献[6]以能耗最小为目标,使用蚁群算法规划了植发机器人工作路径;文献[7]使用5次NURBS曲线插值法拟合机械臂工作轨迹,以运行时间、能量消耗、脉动冲击为优化目标,使用改进人工蜂群算法得到了Pareto最优解集;文献[8]使用4-3-4多项式插值法对关节空间进行轨迹规划,在满足速度约束前提下,使用杂交算法优化了路径点之间的用时。总结机械臂关节空间轨迹规划研究热点和难题,主要包括两个方面:(1)路径点间的拟合函数选取,选取什么样的拟合函数可以获得最好的规划性能;(2)优化方法的选择与改进,使用什么样的方法搜索到最优路径。
针对机械臂关节空间轨迹的时间最优规划问题,本文改进了B样条曲线,提高了对轨迹点的拟合精度;改进了蜂群算法,提高了算法的寻优质量;在满足机械臂运动约束前提下,实现了轨迹的时间最优规划。
2 改进B样条曲线与问题建模
轨迹规划的方法是:根据任务需要和避障要求,确定机械臂起始点、目标点和若干中间点,然后使用某种曲线进行拟合,使机械臂依次经过设定中间点并顺利到达目标点。轨迹规划的目的是在满足约束的前提下,获得时间最短或能耗最小轨迹。
2.1 改进B样条曲线拟合技术
中间点之间的轨迹规划一般使用多项式函数或B 样条曲线,多项式插值函数具有计算量与连续性之间的矛盾,选择B样条曲线规划中间点之间的轨迹。B样条曲线拟合分为近似拟合和插值拟合,近似拟合无法保证经过所有中间点,插值拟合能够经过所有中间点,但是需要将中间点作为型值点反算控制点,此时曲线求解计算量大。为了使B样条曲线经过所有中间点同时不增加计算量,提出了改进B样条曲线拟合方法。
传统三次B样条曲线,如图1所示。由4个控制点P0~P3进行控制。图中为P0P2中点,r0为线段的1/3处;同样地,为P1P3中点,r1为线段的1/3处。B样条曲线起始于点r0,终止于点r1,B样条曲线起点处切线平行于P0P2,终点处切线平行于P1P3。
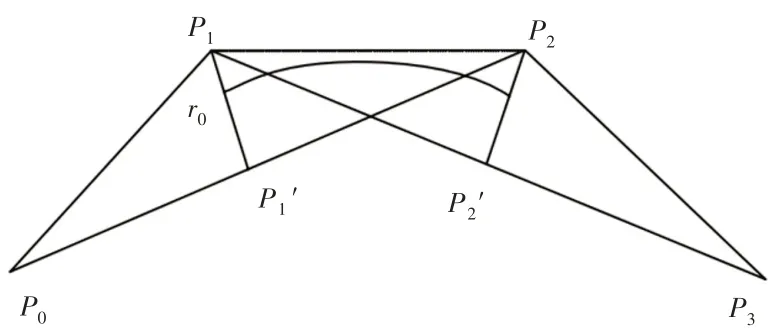
图1 传统B样条曲线Fig.1 Traditional B-spline Curve
从图中可以看出,B样条曲线不经过中间点P0~P3,为了使B样条曲线经过中间点,同时避免插值法中反算过程带来的巨大计算量,本文提出改进的B样条拟合曲线,如图2所示。以B样条曲线经过点P1、P2为例,改进基本思想为:通过增加控制点P1,0、P1,1,使B 样条曲线的起点r0与控制点P1重合;通过增加控制点P2,0、P2,1,使B样条曲线的终点点r1与控制点P2重合。
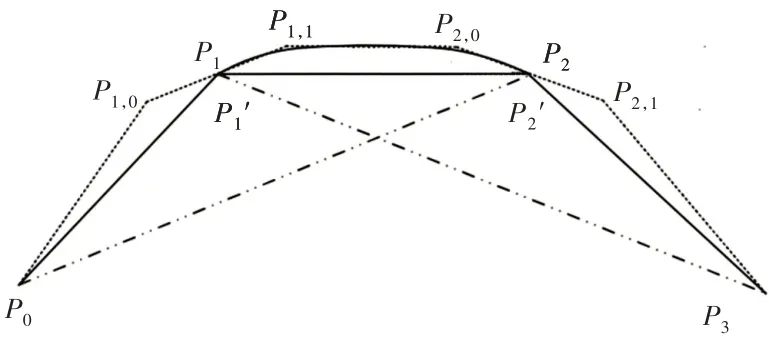
图2 改进B样条曲线Fig.2 Improved B-Spline Curve
改进的具体方法为:以点P1为中点增加控制点P1,0、P1,1,点P1、P1,0、P1,1成一条直线且平行于P0P2,长度P1,0P1=P1P1,1=为底边系数比例。以同样方式在点P2两侧增加控制点P2,0、P2,1。以点P1,0、P1、P1,1、P2,0、P2、P2,1为新的控制点,每连续4个控制点可以确定一段B样条曲线,那么6个控制点可以确定3段B样条曲线。第1段B样条曲线由P1,0、P1、P1,1、P2,0确定,由于P1,0、P1、P1,1在同一直线上,可以将其视为三角形的极限状态,按照传统B样条曲线构造方法,此时点P1、P1′与曲线起点r0重合,即第1段B样条曲线的起点经过中间点P1。同样的,第3段B样条曲线由P1,1、P2,0、P2、P2,1确定,而点P2,0、P2、P2,1在同一直线上,那么第3段B样条曲线的终点必然经过中间点P2。
总的来讲,对于n个中间点,需要将其扩展为3n个控制点,每4个控制点确定一段B样条曲线,规划的曲线必然经过n个中间点,且不存在插值法的反算过程。中间点的扩展控制点为:
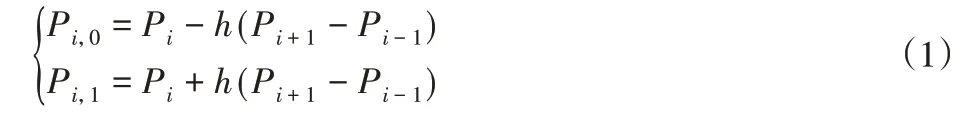
传统的三次B样条曲线方程[9]为:
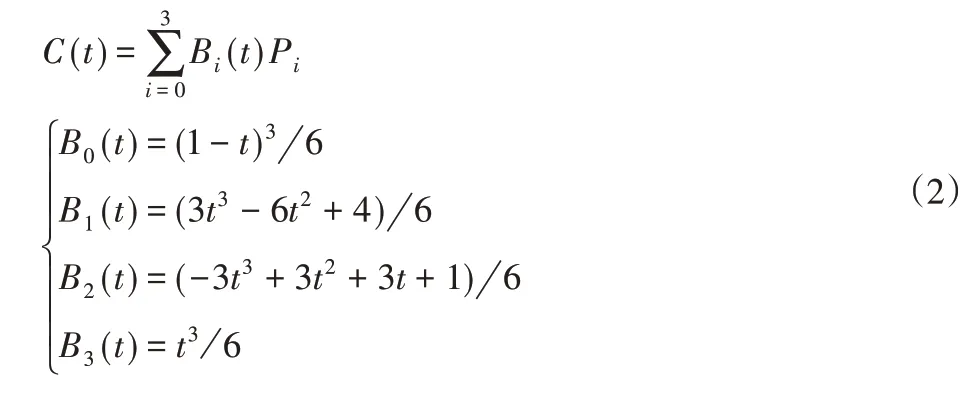
式中:t—变量;Pi—中间点在三维空间坐标;Bi(t)—B样条曲线的样条基。
将式(2)改写为矩阵方式,得到连续3段B样条曲线为:

将式(1)代入式(3),使用原控制点替换掉扩展控制点,得到改进B样条曲线表达式为:

在此需要特别说明的是,式(4)中i不能取0和n-1,因为第一段B样条曲线和最后一段B样条曲线的扩展控制点不满足式(2),只能用式(3)求解。
2.2 时间最优轨迹规划模型
根据机械臂的任务需求、障碍物分布和关节活动范围,确定机械臂执行任务过程中必须经过的若干轨迹点为P0,P1,P2,…,Pm,其中,P0—机械臂末端起始位姿;Pm—机械臂末端终止位姿,使用机械臂逆运动学求解轨迹点对应的关节空间点为θ0,θ1,θ2,…,θm。其中,θi={θij},j=1,2,…n,n为机械臂关节数量。记机械臂末端依次经过点P0,P1,P2,…,Pm的时间为t0,t1,…,tm,这里的规划思路为通过优化机械臂到达各轨迹点的时间,在满足约束条件的前提下,使机械臂在最短时间内由起始点到达目标点。根据规划思路,优化目标函数设计为:

式中:f—机械臂总耗时;Δti=ti-ti-1;i=1,2,…m—由中间点Pi-1运动到点Pi的时间。
机械臂轨迹规划需满足机械臂运动条件,包括关节运动范围约束、角速度约束、角加速度约束、角冲击约束等,以关节j为例,约束条件为:

式(5)与式(6)将机械臂关节空间轨迹规划问题转化为带约束优化问题,此类问题求解方法有梯度法、寻优法等,使用智能算法寻优进行求解。
3 优化搜索策略蜂群算法
3.1 人工蜂群算法
人工蜂群算法是模拟蜂群搜索最优蜜源过程而提出的,将最优蜜源视为优化问题的最优解,蜂群搜索最优蜜源的过程即为优化问题求解过程。算法将蜜蜂人工地分为引领蜂、跟随蜂、侦查蜂三类,三种人工蜂协作完成蜜源搜索[10]。
3.1.1 初始化人工蜂位置。
记人工蜂数量为N,搜索维度为D,以随机方式初始化蜜蜂位置,为:
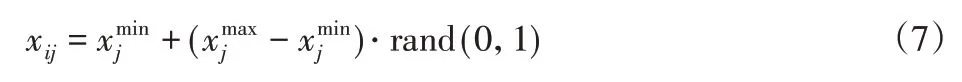
式中:i∈[1,N]—蜜蜂序号;j∈[1,D]—维度;xij—人工蜂位置;—维度j上下界;rand(0,1)—[0,1]间随机数。
3.1.2 引领蜂搜索阶段
引领蜂以交叉方式更新蜜源,即:

式中:vij—引领蜂的蜜源更新位置;xij—原蜜源位置;xkj—随机选择的异于xij的个体;φij—[-1,1]间的随机数。引领蜂使用贪婪规则选择蜜源,即选择xij和vij中蜜源浓度较高的位置。
魏气冲冲走了,迟恒发慌,得赶紧报警,打开手机翻盖,显示屏不亮,按键也无反应,该死的手机!他想去追魏昌龙。就在这时,他看见库区西头变戏法似地亮起了一溜车灯,散在库区的手电光束迅速向北坝中段移动。
3.1.3 跟随蜂选择与搜索阶段
跟随蜂通过摇摆舞了解引领蜂位置蜜源浓度,依据蜜源浓度确定对引领蜂的选择概率:

式中:pi—选择引领蜂i的概率;NB—引领蜂数量;fiti—引领蜂i处蜜源浓度;fi—式(5)构造的目标函数值。通过式(9)给出选择各引领蜂的概率,然后使用轮盘赌方法确定最终选择的引领蜂。跟随蜂选择引领蜂后,在引领蜂邻域内按照式(8)进行位置更新。
3.1.4 侦查蜂搜索阶段
当某只蜜蜂迭代次数达到设定上限但是适应度却没有明显提高时,此蜜蜂放弃此处蜜源转化为侦查蜂,以随机的方式生成新位置,方法与式(7)一致。
3.2 优化搜索策略蜂群算法
为了平衡算法多样性和收敛性,对引领蜂和跟随蜂的蜜源搜索策略进行改进。
3.2.1 基于最优解引导的引领蜂蜜源搜索
文献[11]中提到“DE/rand-to-pbest/1”突变策略可以很好地保持种群差异性,参考这一思想,将引领蜂蜜源搜索策略改进为基于最优解引导的邻域学习策略,即:
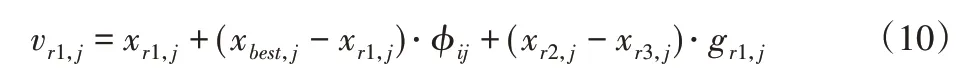
式(10)给出的位置更新策略,如图3所示。
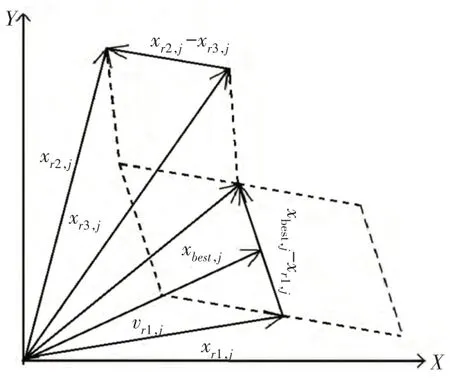
图3 引领蜂搜索方式Fig.3 Searching Mode of Leading Bee
以xr1位置向量为基向量,在伸缩因子ϕij的作用下使vr1以不同程度向xbest靠近,保证了蜜蜂位置朝着更优方向前进。式(10)中第三项通过高斯缩放因子调节xr2-xr3的步长,使vr1以xbest-xr1为中心分布线,向两侧呈现高斯分布。根据高斯分布特性,vr1以68.27%的概率分布在xbest-xr1两侧(-α,+α)范围内,保证了以大概率在最优解邻域内搜索;vr1以31.73%的概率分布在(-α,+α)以外,对于探索新区域、开发新蜜源、增加多样性意义重大。
3.2.2 基于三角变异的跟随蜂蜜源搜索
此部分内容对跟随蜂的蜜源搜索方法进行改进。以人工蜂xr1的位置更新为例,在种群中随机选取异于xr1的两只相邻人工蜂xr2、xr3,三个相异个体组成一个超几何三角形,利用三角变异引导人工蜂向三者中最优者靠近,方法为:
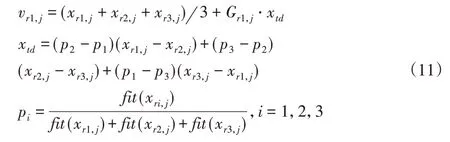
式中:Gr1,j—高斯分布缩放因子,即Gr1,j∼N(0,β);xtd—位置扰动量;xr1、xr2、xr3—相邻人工蜂;p1、p2、p3—由各自适应度构造的影响概率。
式(11)给出的三角变异蜜源搜索方法,如图4所示。以三角形中心位置为基向量,各边向量对基向量的扰动大小依据适应度函数而构造,使得基向量向三个人工蜂中最优位置靠近,这种蜜源搜索方法可以保证跟随蜂向适应度靠前的33.3%蜜蜂靠近,达到了位置更新进化的目的。另外,高斯伸缩因子的作用与式(10)中一致,这里不再分析。
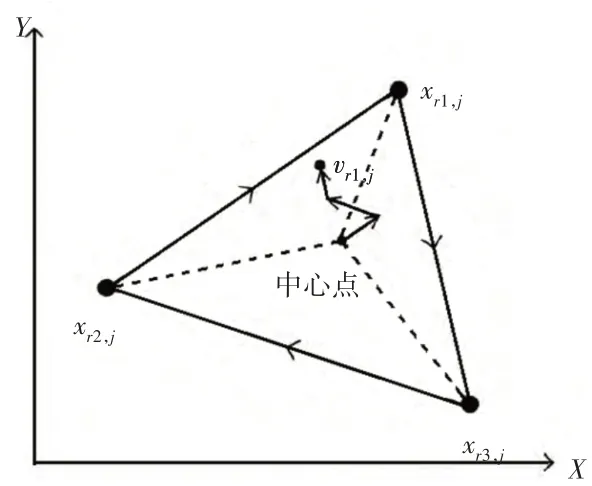
图4 跟随蜂搜索方式Fig.4 Searching Mode of Following Bee
3.3 优化搜索策略蜂群算法流程
前文对引领蜂和跟随蜂的蜜源搜索策略进行了改进,并未对算法流程产生影响,因此此处给出的算法流程既适用于改进蜂群算法,也适用于传统人工蜂群算法,如图5所示。
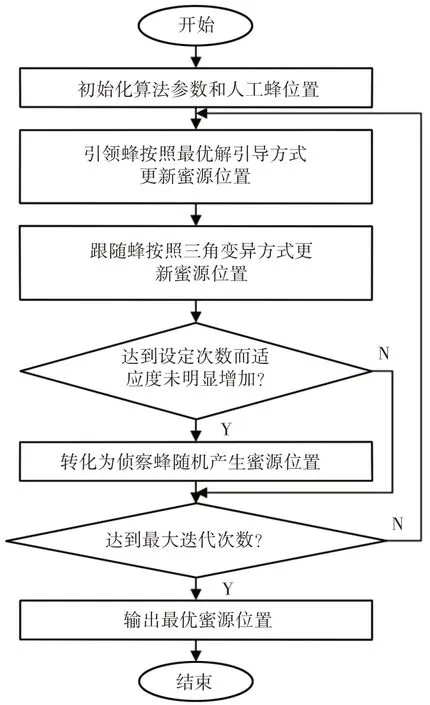
图5 优化搜索策略蜂群算法流程Fig.5 Searching Strategy Improved Bee Swarm Algorithm Flow
4 仿真验证与分析
仿真验证包括两个方面内容,一是验证B样条曲线与改进B样条曲线的拟合精度,二是验证优化搜索策略蜂群算法的轨迹规划性能。
4.1 改进B样条曲线拟合精度验证
前文中提到,B样条曲线使用拟合法时无法保证经过所有中间点,插值法能够经过所有中间点但是存在反算引起的大量计算问题,改进B样条曲线使用拟合法确保了经过所有中间点,在此对其拟合精度进行验证。以抛物线y=(x-4)2为例,在[0,8]区间内均匀生成9个中间点,分别使用B样条曲线拟合法和改进B样条曲线拟合法结果,如图6所示。
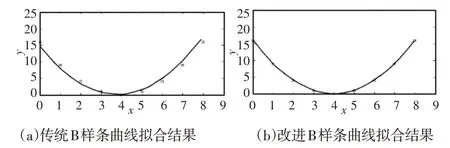
图6 B样条曲线拟合精度Fig.6 B-Spline Curve Fitting Accuracy
统计B样条曲线和改进B样条曲线在9个中间点处的拟合误差标准差,B样条曲线的拟合误差为0.082,改进B样条曲线的拟合误差为0.041,比传统B样条曲线的拟合精度提高一个数量级以上,说明了改进B样条曲线能够更加精确地经过中间点,同时改进B样条曲线计算过程中不存在反算过程。
4.2 优化搜索策略蜂群算法规划性能验证
以PUMA560机械臂为研究对象,此机械臂具有6个活动关节,具体构型可参考文献[12],这里不再赘述。PUMA 机械臂的活动能力约束,如表1所示。
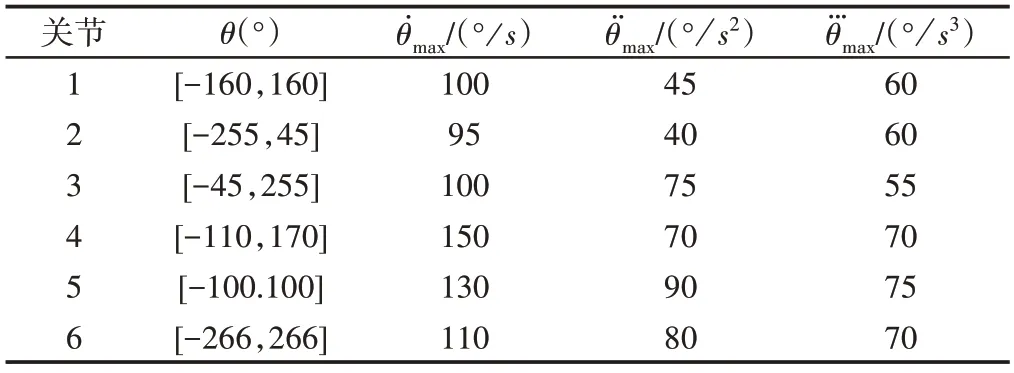
表1 PUMA560活动能力约束Tab.1 Mobility Constraint of PUMA560
在PUMA560机械臂可到达范围内设置6个轨迹点,如表2所示。表中:θ0—轨迹起点;θ5—轨迹终点;θ1~θ4—必须经过的中间点。
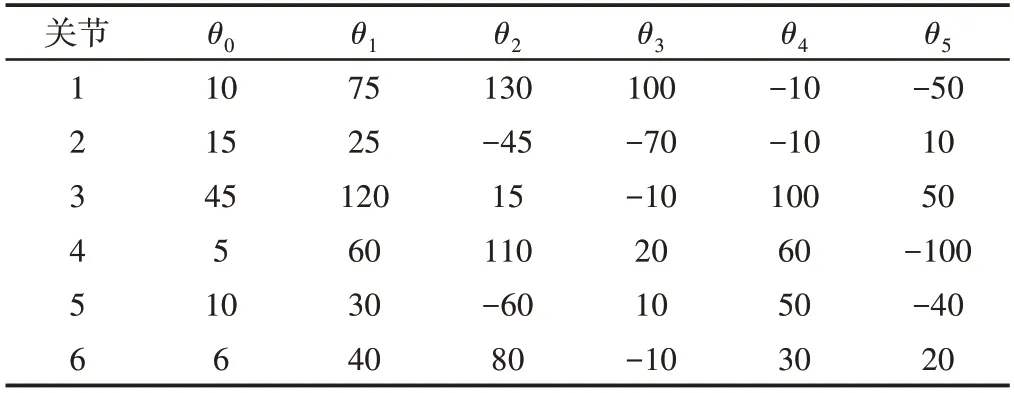
表2 轨迹点Tab.2 Trajectory Point
使用人工蜂群算法和优化搜索策略蜂群算法对问题进行求解,算法参数统一设置为:种群规模N=40,粒子维度D=5,最大迭代次数tmax=400,单个位置迭代限度为tlimit=20,将任意相邻两点间耗时限制在4s内,则每个维度搜索空间为(0,4],高斯收缩因子参数α=1、β=0.1。两种算法各自独立运行10次,选择两个算法各自的最优解进行展示,最优解的目标函数值随迭代过程变化曲线,如图7所示。
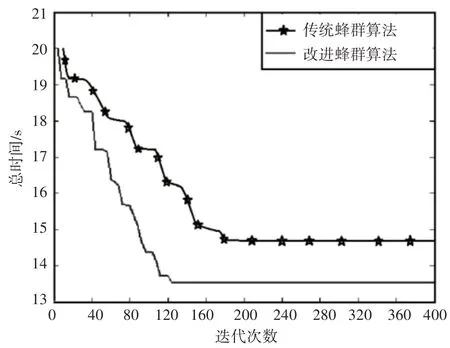
图7 迭代曲线Fig.7 Iteration Curve
从图中可以看出,优化搜索策略蜂群算法在迭代至120次时算法搜索到最优解,最优解为13.5141s;传统人工蜂群算法迭代至200次时搜索到最优解,最优解为14.8726s。人工蜂群算法和优化搜索策略蜂群算法搜索到的最优解位置,如表3所示。

表3 优化结果Tab.3 Optimizing Result
结合图7和表3,从搜索到最优解时迭代次数看,改进算法比传统算法提前了80次;从最优解质量看,改进算法比传统算法减少了1.3585s,即机械臂工作耗时减少了9.13%。
这是因为改进算法中引入了基于最优解引导的引领蜂蜜源搜索和基于三角变异的跟随蜂蜜源搜索方法,改进的蜜源搜索方法以大比例促进算法向最优解附近靠近,同时以相当比例允许蜜蜂大范围搜索,兼顾了多样性。而传统算法向邻解学习方式,不仅学习效率低,而且由于邻解学习价值小,使算法收敛速度也较慢。
根据改进算法搜索的最优蜜源位置和改进B样条曲线规划方法,给出PUMA560机械臂6个关节角轨迹,如图8所示。
结合表1和图8可以看出:(1)改进蜂群算法规划的关节空间轨迹满足动力学约束,可以进行实际应用;(2)6个关节的起点和终点角速度均为0,与实际情况相符;(3)改进B样条曲线精确地经过了所有轨迹点,相应地机械臂末端精确的经过了设定点。由以上三点可以看出,改进蜂群算法和改进B样条曲线规划的轨迹在满足约束条件,实现了时间最优,可以应用于实际。
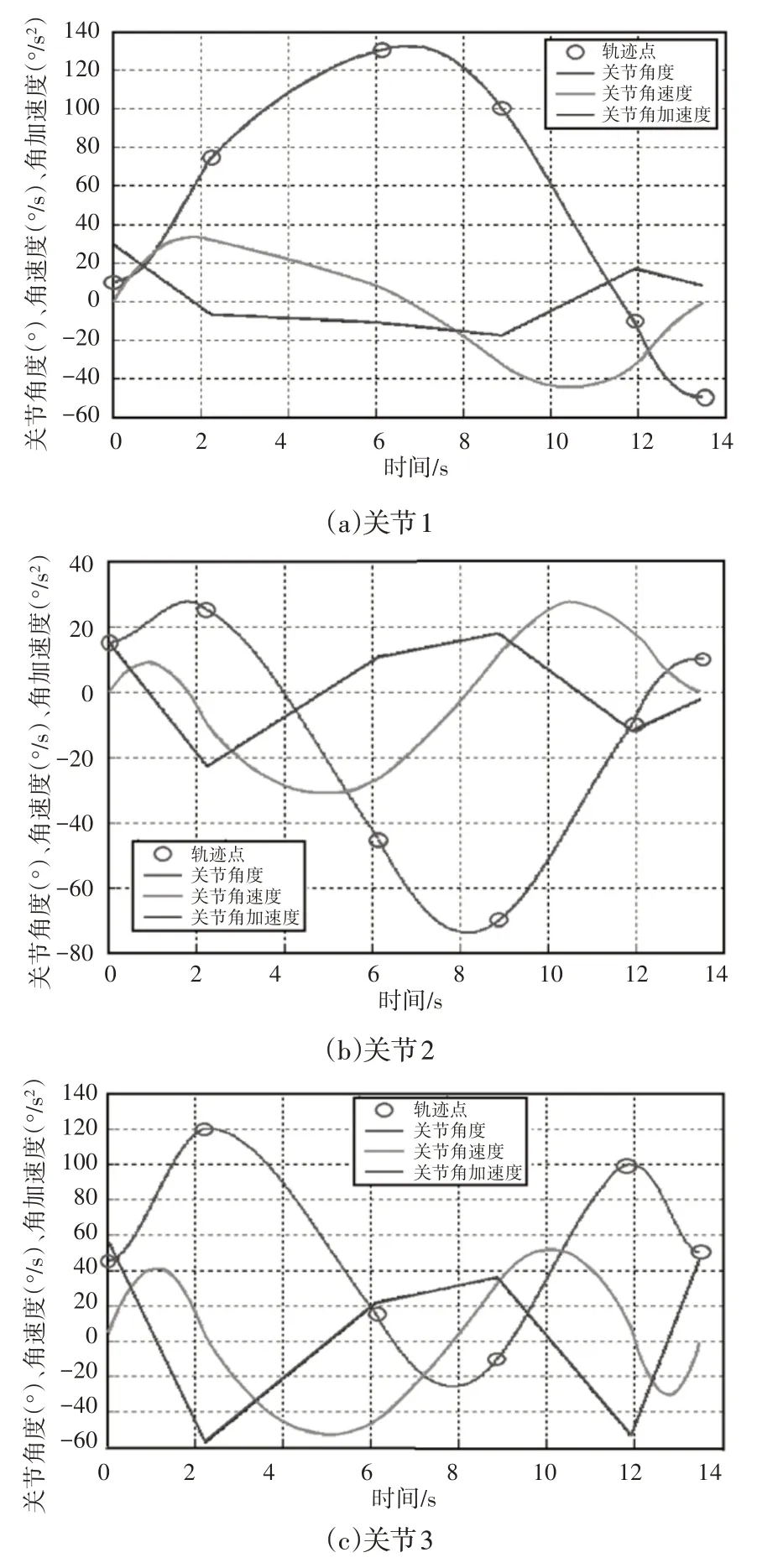
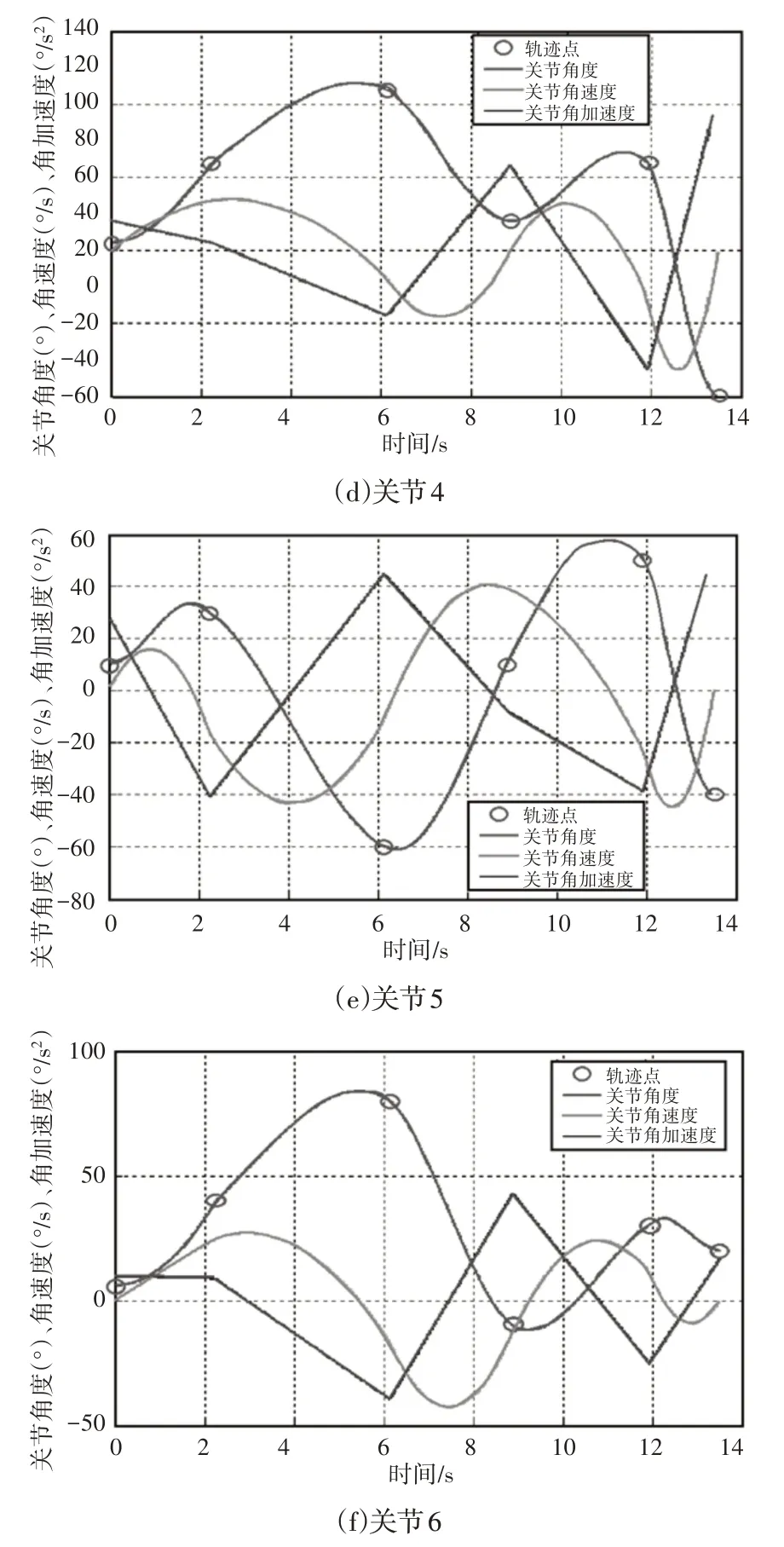
图8 关节角轨迹Fig.8 Joint Angle Trajectory
5 结论
研究了机械臂关节空间的时间最优轨迹规划问题,改进了B样条曲线和蜂群算法,经仿真验证得出了以下结论:
(1)改进B样条曲线使用拟合法,在不增加计算量同时,提高了对轨迹点的拟合精度;
(2)优化搜索策略蜂群算法规划的轨迹满足约束条件,实现了时间最优,可以进行实际应用。
