基于RBF神经网络滑模的多电机同步控制方法
2022-09-22谢国民孙少华徐耀松
谢国民,孙少华,付 华,付 昱,徐耀松
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛125105)
0 引言
近年来,随着工业机械加工精度的提升,多电机同步控制技术成为研究的热点[1-3].多电机驱动系统中各电机间借由信息交互实现同步的系统状态,广泛应用到需大量协同工序的工业生产中.学者们通过对多电机系统控制结构、控制算法等方面深入研究,取得了丰硕的成果,大大提升了多电机系统同步性能.
目前,多电机同步控制连接结构分为刚性耦合、柔性耦合和无耦合连接:刚性耦合电机间通过硬介质连接,存在极易磨损、振动等问题;柔性耦合电机间通过柔性介质如皮带等连接容易产生打滑的现象;无耦合连接则去除了这些实物连接介质,通过将转速、转矩等特征量融入控制器中,实现电机间的同步控制.以这些连接结构为基础,学者们提出了许多改进的同步控制策略.DENG H等[4]设计了一种用于多电机同步控制系统模糊支持向量机(FSVM)的控制器,收敛速度快,鲁棒性强,但模糊规则的制定依赖于经验,难以应对复杂的多电机系统.曹春平等[5]则在建立4台电机模型基础上,提出了神经网络PID结合偏差耦合的控制方法,提升了多电机同步控制系统的抗扰能力,但PID环节的使用难以保证跟踪速度与鲁棒性能.胥小勇等[6]在多电机同步控制结构中引入了比例环节,增强耦合性能且结构简单,但在鲁棒性能上改进较少.文献[7]、文献[8]则将关注点集中在含有机械连接多电机同步控制里,针对各机械部分存在磨损大及精度差的劣势,提出一种虚拟总轴的多电机耦合控制结构,拆分同步误差与跟踪误差之间的耦合,分别求解,为多电机同步控制分析提供新思路,但增加了运算量,且对大规模系统难以适用.文献[9]采用积分期望补偿直接/间接自适应鲁棒控制技术合成同步控制器,实现了精确的参数估计和对各种不确定性的隔离鲁棒性能,但仅用于两台电机同步系统;文献[10]利用电机位置补偿方法对多台电机进行精确跟踪,采用电机位置信号补偿三电机之间的同步误差,但在鲁棒性上不够理想.文献[11]将滑模控制(sliding-mode control,SMC)与模糊控制应用到多电机同步控制控制中,保证鲁棒性的基础上简化了计算过程,但在控制精度与参数量化上无法满足要求,使系统存在较大抖振.文献[12]给出了 2台电机利用神经网络滑模实现鲁棒控制的方法,有效提升电机鲁棒性能,但仅考虑直线电机模型.
RBF神经网络具有对模型未知部分实现自适应无限精度逼近的能力[13],已在电动助力制动系统[14]、风机机构应力设计[15]、耐腐蚀材料制造[16]上取得一定成果,但鲜有将其应用到多电机同步控制性能改善上;刘福才等[17]指出随着工业自动化水平提升,生产传输线以及功率的提升催促多电机同步控制向着电轴方向发展,并且电机间的耦合为同步控制带来复杂度提升的同时,也为同步精度与鲁棒性的提升提供了更多可能,应该扬其长而避其短.虽然在多电机同步控制领域,学者们提出了诸如相邻耦合[18]、虚拟总轴[19]、环形耦合[20]等控制结构,但多电机同步控制在注重电机间同步误差的同时,更应考虑各电机跟踪误差的影响,如何同时兼顾两种误差使多电机系统鲁棒性能提升的同时削弱抖振,是多电机同步控制应用到工业生产中亟待解决的问题.
针对上述问题,提出基于 RBF神经滑模的控制方法,并搭配无耦合连接中的相邻交叉耦合控制结构,实现对多电机系统的鲁棒控制,利用李雅普诺夫稳定性定理判定系统的稳定,在Matlab/Simulink中进行电机同步运行的仿真,并与传统控制方法比较,结果证明了所提控制方法不仅能有效实现多电机的同步控制,且大大抑制了系统抖振.
1 三相永磁同步电动机的数学模型
永磁同步电动机(permanent magnet synchronous motor,PMSM)响应速度快、运行范围广,又不存在换向问题,非常适于应用到多电机同步控制中,根据PMSM原理,可得到消除耦合后的d、q坐标系下电机状态方程为
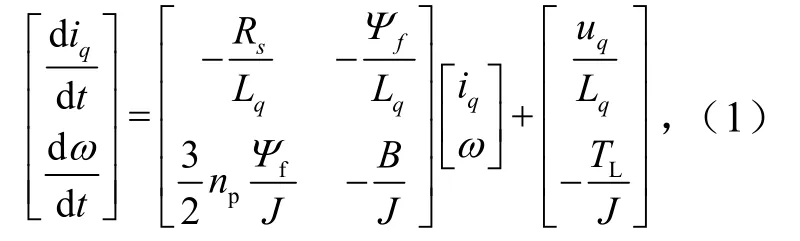
式中,id,iq为d、q轴的电枢电流分量,A;Ld,Lq分别为d、q两轴的等效电枢电感分量,mH;Ψd,Ψq为d、q两轴的定子磁链分量,Wb;Ψf为电机的转子磁链;ud,uq为电机电枢电压在d、q两轴的分量,V;Rs为电机电枢绕组的电阻,Ω;np为电机转子极对数;ω为电机转子角速度,rad/min.
不难看出,id,iq磁链之间已无耦合,则控制电枢电流iq可线性控制电磁转矩,考虑参数和负载扰动的名义值,运动方程为
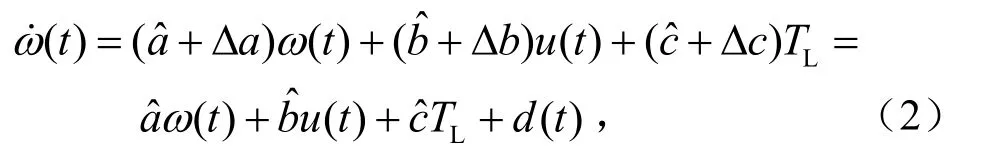
2 相邻交叉耦合结构
相邻交叉耦合控制并不需要设定基准电机,对每个需要控制的电机,只考虑与其相邻的两电机状态,因而不存在因主电机扰动而造成系统失稳的情况,使得整个系统的稳定性得到大大提升.这种控制结构在尽量简化控制过程的基础上,同时计及了跟踪误差与同步误差,具有良好的鲁棒性.
设第i台电机转速的跟踪误差为
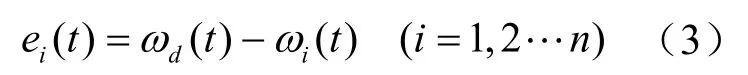
式中,ωd为参考角速度,rad/min;ωi为实际角速度,rad/min.在多电机同步系统运行中,既要确保ei→ 0 ,还要使n台电机跟踪误差满足
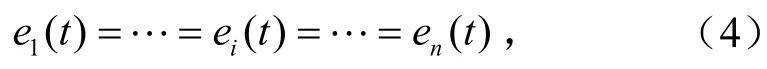
同理定义同步误差为

则对于第i台电机的相邻速度耦合误差算式为

若对所有电机,都满足εi→0,则可实现多电机同步运行的控制目标,图1为相邻交叉耦合控制结构下四电机同步控制.

图1 四电机同步系统控制结构Fig.1 motor synchronous system control structure drawing
图1中,跟踪误差控制器用来消除单台电机的跟踪误差.同步误差控制器则用来消除每台电机与相邻两台电机之间的同步误差,从而达到系统的多电机同步控制.
考虑到在仿真过程中,对永磁同步电动机的控制需要加入较多变换环节,使过程变得繁琐,因此采用S函数来搭建PMSM本体模型,在保证所需电机特性的基础上,省去变换模块,且电机参数方便修改,还可使电机控制过程得到简化.该模块输入的是d、q坐标系下的电枢电压值和机械负载转矩值,输出的是d轴电枢电流、q轴电枢电流、电磁转矩以及转速.
3 多电机同步控制的神经滑模算法
3.1 滑模控制器设计
滑模变结构控制因鲁棒性强、控制结构简单而广泛应用到多电机同步控制中,取得较好效果.设计系统跟踪误差滑模面为
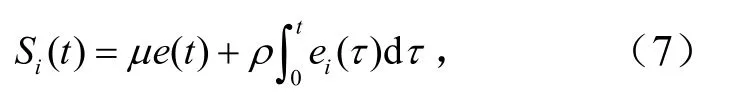
式中,μ,ρ>0.则
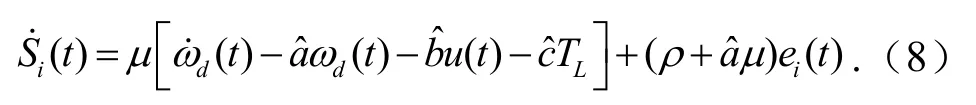
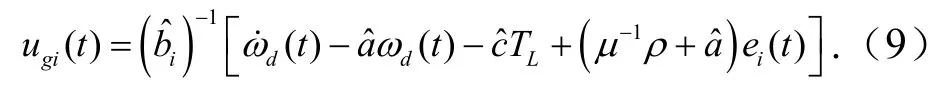
设计切换控制律为
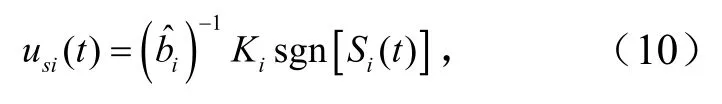
式中,Ki为切换增益,设Ki=Ni+γ,γ>0.
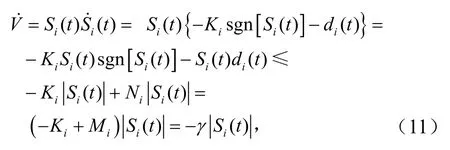
据以上条件可得
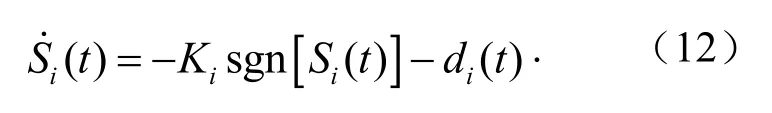
对所设计的控制律,分析系统的稳定性,设Lyapunov函数为其导数为
因此,依据李雅普诺夫稳定性判定定理可得系统是全局渐近稳定的.
设计第i台电机的同步误差滑模面为
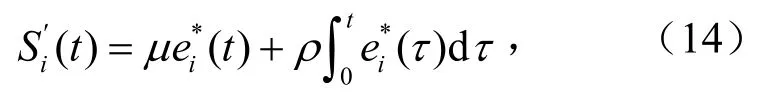
则据以上算法,可得第i台电机的同步误差控制器输出为
且是全局渐近稳定的.
总而言之,单电机跟踪控制律uGi(t)和同步误差控制律uTi(t)两部分构成了第i台电机总控制律ui(t),即

3.2 神经滑模算法
RBF以其能逼近任何函数而成为神经网络算法中的一个重要研究方向,利用RBF神经网络的强大映射能力优化滑模控制器的控制切换增益,使数据逼近标准,减小滑模控制器的“抖振”,实现自适应函数的优化控制.本文将[SS˙]作为 RBF神经网络的输入,优化滑模切换增益K,提出基于RBF神经滑模的控制方法(RBF–SMC).

RBF径向基向量为H= [h1,h2,… ,hm]T,高斯核函数hi可表示为
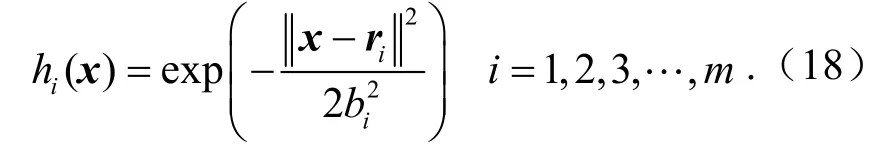
RBF第i个节点中心向量ri=[ri1,ri2,… ,rim];设网络基宽向量为B*= [b1,b2,… ,bm]T,网络中的权值向量W= [w1,w2,… ,wm]T,节点i的基宽参数bi> 0 ,RBF输出为

神经网络权值调整的指标为

利用梯度下降法对网络权值优化

式中,n1为网络学习速率,n1∈( 0,1).
网络权值学习算法为

式中,α为惯性量系数,α∈ ( 0,1).
以一台电机为例,算法流程见图2,控制结构原理图见图3.由图2与图3可知,所设计控制结构仅需要对速度控制器部分改进,其结构简单,利于工程推广.
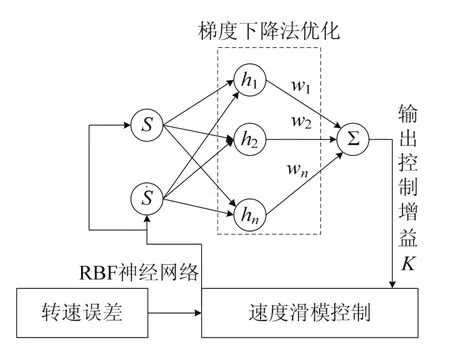
图2 神经滑模控制流程Fig.2 flow of neural sliding mode control
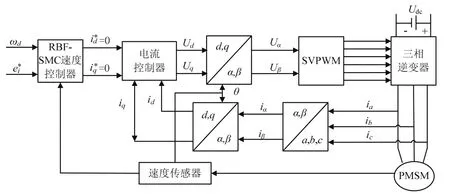
图3 第i台电机控制结构原理Fig.3 schematic of the control structure of i motor
4 仿真实验及分析
4.1 算法验证
为验证RBF神经网络算法的优越性,给定一组随机变量,BP与RBF的跟踪比对结果示于图4,其中R2为[0,1]内的决定系数,其值愈接近1,则性能更占优.
由图4可知,BP神经网络的决定系数为0.878 05,而RBF神经网络的决定系数为0.929 96,性能更优.
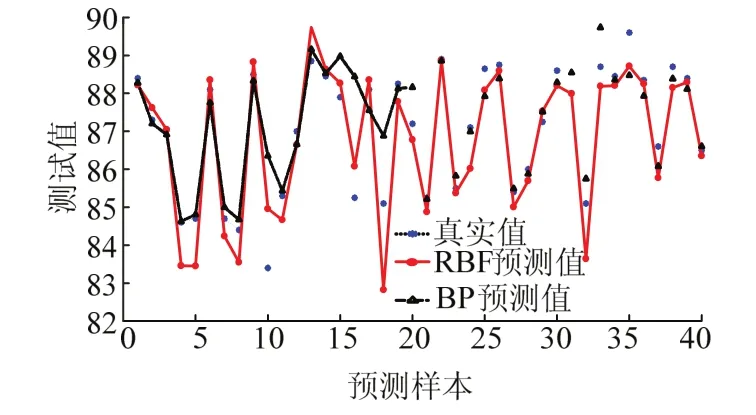
图4 BP与RBF预测结果对比Fig.4 comparison of prediction results between BP and RBF
4.2 相邻交叉耦合控制结构验证
为验证所提控制结构的优越性,与常用的几种控制结构进行对比分析.仿真时选用三台电机同步运行的模型,参考转速统一选择1 000 rad/min,并且扰动均加在第二台电机,数值为 10 N·m.所用电机参数见表1,电机1、电机2、电机3的跟踪误差见图5,同步误差见图6.对比结果见表2.
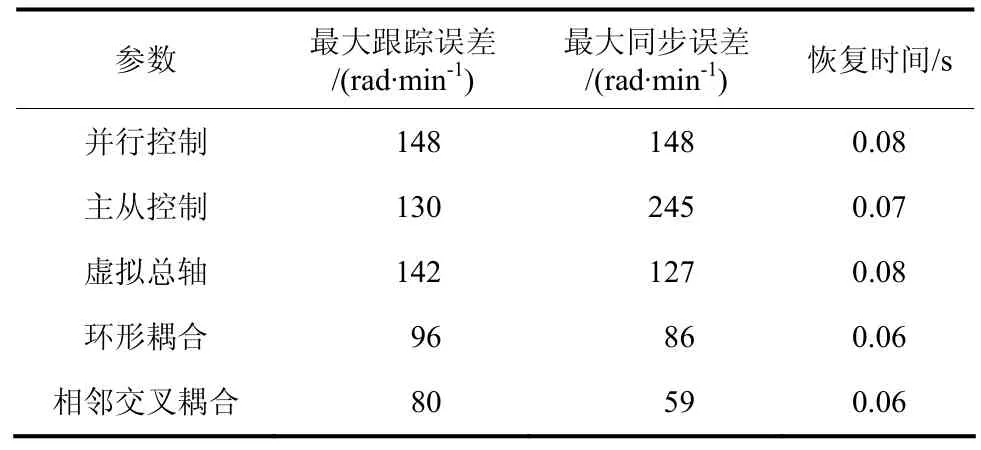
表2 对比结果Tab.2 comparative results
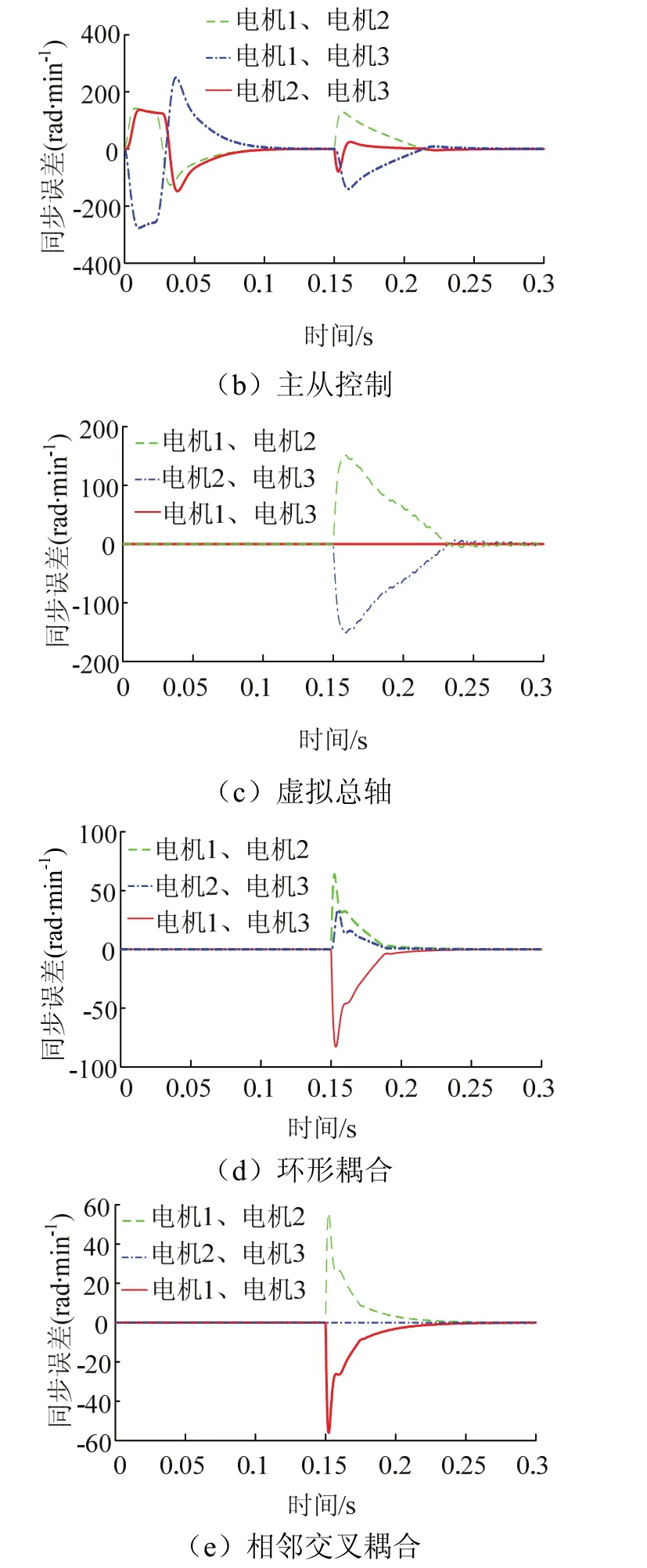
图6 电机转速同步误差对比Fig.6 comparison of serrors

表1 实验所用电机参数Tab.1 motor parameters used in the experiment
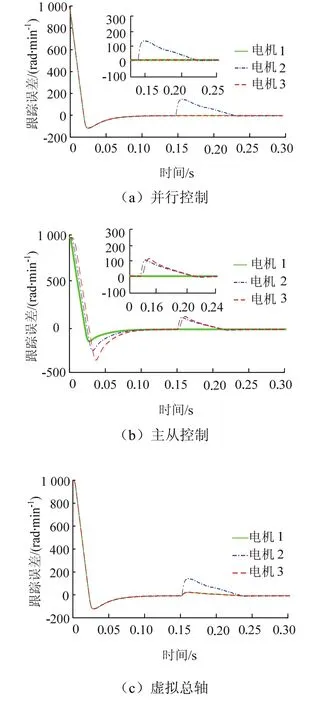
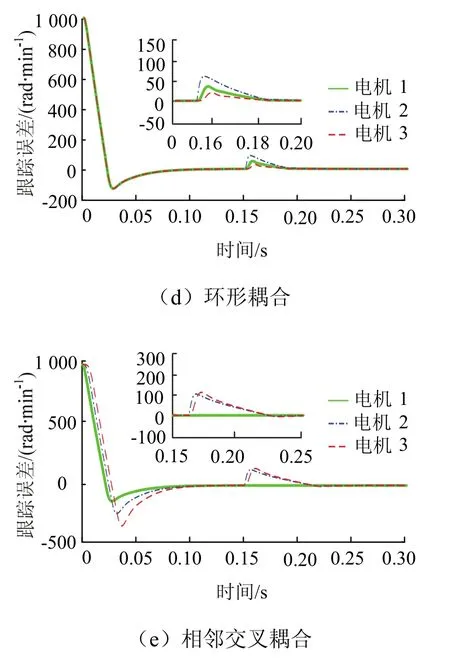
图5 电机转速跟踪误差对比Fig.5 comparison of tracking errors

由表2可知,并行控制电机间相互独立,仅跟踪参考转速调节,调节效果最差;主从控制中从属的电机间无耦合,调节效果亦不理想,且启动过程环境恶劣;电子虚拟总轴控制改善了启动,但调整中存在一定抖动;环形耦合控制虽在指标上有所改善,但因其仅跟随相邻一个电机,故在精度与鲁棒性上难以满足要求;而所提相邻交叉耦合结构在启动、扰动各过程中最大误差80 rad/min,恢复时间仅0.06 s,表现优于前面几种结构.
4.3 RBF-SMC验证
实验参数设定:μ=ρ= 1,γ=10,网络学习参数取δ= 0.80,α= 0.05,ω= 1 00rad/min;PI控制器所用参数:跟踪控制器比例系数kp1= 0.42,积分系数ki1=0.1,同步控制器比例系数kp2= 2.46,积分系数ki2= 0.38.
图7为电机1在给定转速ω= 1 00rad/min下启动时转速波形,由图可知,PI控制有近10%的超调量,直到0.04 s后才趋于稳定,因而具有超调量大、调整缓慢的缺点;SMC虽启动时间快,但同样有3%的超调量,且抖振明显;而本文所提RBF-SMC能够在短时间内平稳启动,基本无超调,且能有效防止抖振.
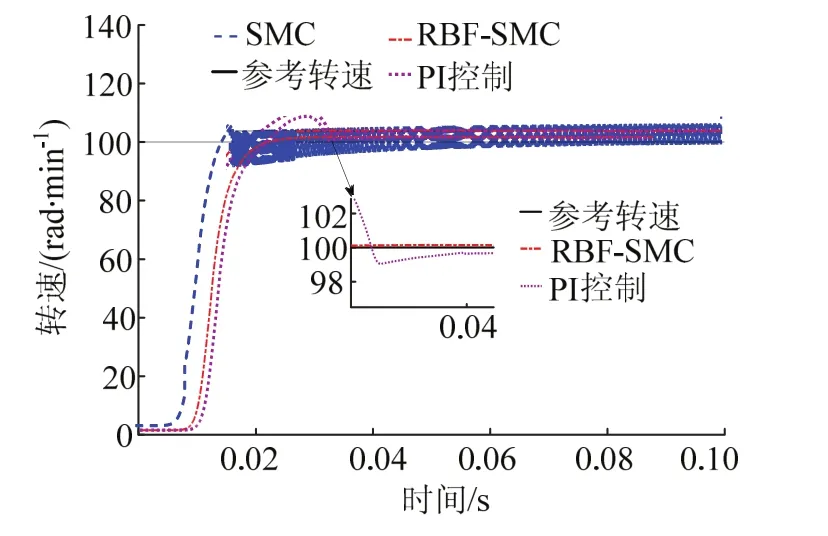
图7 电机1启动转速Fig.7 rotational speed motor 1 at startup
在1.12 s突加扰动时,电机1的转速曲线见图8,从图中可以看出,采用SMC方法时,转速波动较大,而采用RBF-SMC则避免了此种情况,表明其鲁棒性较强.
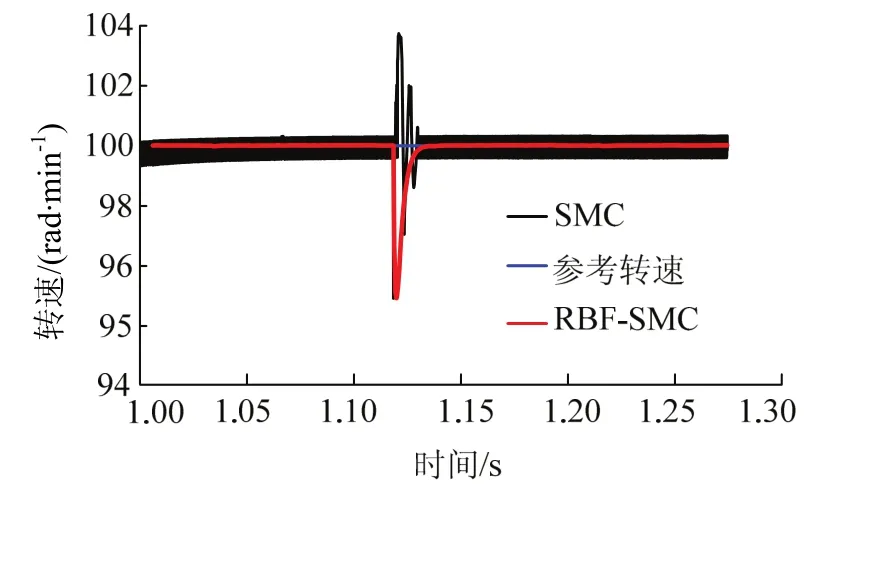
图8 电机1在负载扰动时的转速Fig.8 speed of motor 1 during load disturbance
4.4 实验验证
为验证所提控制方法的有效性,在实验室中搭建PMSM实验平台,参数如下:电机额定功率为10 kW,额定电压 380 V,定子电阻 0.425 Ω,定子电感6.55 mH,交直轴电抗为2.35 Ω.实验平台见图9.

图9 电机实验平台Fig.9 motor experiment platform
为了验证本控制方法的动态性能,电机参考转速在50 rad/min和80 rad/min间转换2次,传统滑模变结构控制与RBF-SMC控制下实验结果见图10、图11.
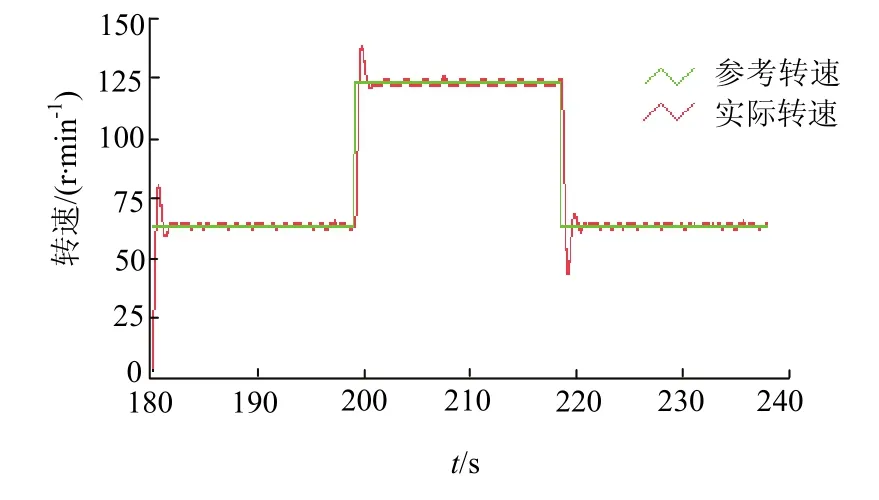
图10 SMC控制电机转速Fig.10 speed of motor controlled by SMC
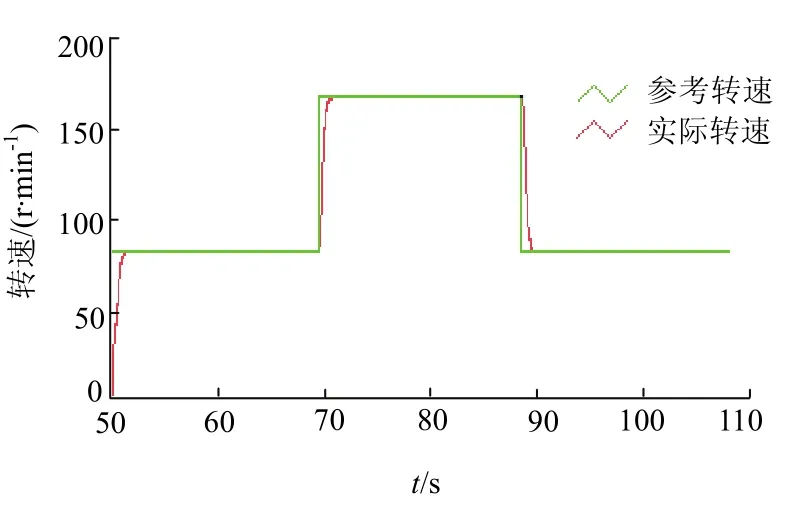
图11 RBF-SMC控制电机转速Fig.11 speed of motor controlled by RBF-SMC
可以看到传统 SMC控制不仅调整过程效果不好,超调量为 7%,且存在严重的抖振现象,而所提 RBF-SMC不仅没有超调,且克服了抖振现象.值得指出的是,因实验室条件有限,无法进行多台电机的验证,将会在以后的工作中完成.
5 结论
(1)对多电机同步控制进行了研究,完善了相邻交叉耦合在多电机控制中的收敛性能,并在此基础上设计了基于RBF神经网络的滑模控制器,利用 RBF神经网络的强大映射能力优化滑模控制器的控制切换增益,使数据逼近标准,减小滑模控制器的“抖振”,实现自适应函数的优化控制,引用李雅普诺夫证明了其稳定性.
(2)实验结果表明,所提方法应用到多电机同步控制中,可同时兼顾跟踪与同步误差,且既不牺牲鲁棒性又可有效减弱抖振,对于研制高性能的同步控制器具有一定的指导价值.
