Microcrack-and microvoid-related impact damage and ignition responses for HMX-based polymer-bonded explosives at high temperature
2022-09-22HijioXueYnqingWuKunYngYiWu
Hi-jio Xue ,Yn-qing Wu ,*,Kun Yng ,**,Yi Wu
a State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China
b School of Aerospace Engineering,Beijing Institute of Technology,Beijing,100081,China
Keywords:PBX Thermal-mechanical coupling Numerical simulation Impact Sensitivity
ABSTRACT Investigating the damage and ignition behaviors of polymer-bonded explosive(PBX)under a coupled impact and high-temperature loading condition is required for the safe use of charged PBXs.An improved combined microcrack and microvoid model(CMM)was developed for better describing the thermal effects of deformation,damage,and ignition responses of PBXs.The main features of the model under typical dynamic loadings(i.e.uniaxial tension and compression,and lateral confinement)at different initial temperature were first studied.And then the effects of temperature on impact-shear sensitivity of HMX-based PBXs were investigated.The results showed that the ignition threshold velocity of shear-crack hotspots exhibits an increase from 260 to 270 to 315—325 m/s when initial temperature increases from 301 to 348 K;and then the threshold velocity decreases to 290—300 m/s with the initial temperature continually increasing to 378 K.The predicted ignition threshold velocity level of the explosives under coupled impact and high temperature loading conditions were consistent with the experimental data.
1.Introduction
During the storage and transportation stage,charged polymerbonded explosives(PBXs)could encounter a series of extreme loading scenarios,for example,impact,cook-off,flame-treated,which will greatly increase the risk of accidental ignition of PBXs and cause numerous catastrophic tragedies[1—6].Compared to a single impact stimuli,the PBXs under a coupled impact and hightemperature loading condition will exhibit a more complicated ignition behavior due to the coupled mechanical-thermal effects.Thus,it's urgent to investigate the potential damage and ignition responses of PBXs under a coupled impact and high-temperature loading condition,for better evaluating the safety and survivability of charged PBXs.
In the past decades,many experimental and numerical studies were performed for respectively investigating the ignition of PBXs under impact and high temperature.The Steven impact test[7]has been widely used to study impact sensitivity.The test was developed to determine the critical impact velocity of a metal-encased explosive in response to a low-velocity impact of a steel projectile[8].Zhang et al.performed the modified Steven test for highly explosives with different thicknesses and studied the mechanism to the mechanically induced reaction[9].Gushanov et al.presented an initiation model for explosive under low-velocity impacts and the predicted characteristics of explosive initiation were qualitatively agreed with experimental data[10].Vandersall et al.modeled the crush,puncture,and perforation scenarios using different-shape projectiles,and proposed different aspects of ignition mechanisms,including friction,shear,and strain[11].Regarding to the coupled thermal and mechanical loading condition,the thermalmechanical coupling effects should be taken into consideration.Various cook-off tests were designed for investigating the thermal safety of the explosive charge[12,13].Switzer et al.carried out Steven tests to analyze the influence of temperature on the threshold velocity of warhead at which explosives react[14].The microstructure of the charged explosive may alter under impactand high temperature loading and influenced by the temperature and load intensity,and duration[15].Therefore,a constitutive model incorporating the effect of temperature on the microstructure is required to accurately predict the failure and ignition of PBXs under different temperature.
In contrast to the single impact loading,the damage mechanisms of PBXs at high-temperature would become increasing complicated due to several factors,including the phase change of explosive crystal[16],the endothermic or exothermic properties of binder[17],and the large differences between crystal and binder.Several experimental works focused on interpreting the complicated relation between thermal damage and impact sensitivity.Dickson et al.suggested an intimate coupling between thermal and mechanical behavior during the thermal ignition[12].Forbes et al.[18]and Sandusky et al.[19]showed that the ignition threshold velocity of PBXs would decrease with cook-off temperature increasing.The tensile strength of PBX decreases with the rise of temperature.When the temperature is higher than 75C,the tensile strength is lower than 0.5 MPa.The tensile strength approaches zero when the temperature exceeds 80C.At this point,the PBX will exhibit the properties of viscous flow with minimal strength.In addition,the strain rate will reach a high value 10seven for low-velocity impacts[20].The experimental results of Dai et al.[21]showed a first-dropping and second-rising tendency of impact sensitivity with the increase of pre-heating temperature.From above,although some impact-high temperature experimental data were obtained,the influence of temperature on PBX impact initiation and its fundamental mechanisms are still poorly understood.
Plenty of continuum-scale numerical models have been developed to predict the impact ignition response of PBXs;however,few models are feasible to describe both the thermal effects and lowintensity impact ignition of PBXs[22,23].Dienes et al.[24]established a coupled chemical-reaction-ignition model based on the relative frictional heating effect between closed microcrack interfaces in explosive grains as the heat-generating mechanism for the formation of hot spots.The model considers the influence of the melting of explosive crystals during heating and the temperaturedependent viscosity on the ignition,while the general temperature effect was not taken into account.Li et al.explored the creep performance of a kind of PBX containing TATB and its creep compliance function expression,discovering that the compressive mechanical properties strongly correlate with temperature and a transition temperature range of 40—60C is evident.The creep compliance function simulated by the Prony series was in good agreement with the experimental superposition principal curve.Because the timescale for the ignition of hotspots(~10 μs)is much shorter than that for the material creep(~4 h),the model is not suitable for low-intensity impact[25].Lou et al.used a coupled mechanical-thermal-chemical model to study the deformation of target plate and the ignition threshold velocity of explosive under the standard Steven test,while this model was failed to accurately describe the complex physical and chemical processes[26].The present work develops a combined microcrack-and microvoidrelated hotspot model which considers the effects of ambient temperature on deformation,damage evolution,and ignition of low-intensity impacted PBXs.
The present study seeks to establish a SCRAM—based model to describe the influence of the initial temperature on the viscoelasticplastic deformation,cracking damage,and ignition behavior of PBXs under low—velocity impact.The current model improves the combined microcrack and microvoid(CMM)model by considering(i)the thermal softening response of material and(ii)the effects of temperature on evolution of microcracks and microvoid.The aim of this work is to predict the damage and ignition behaviors of PBXs under a coupled impact and high-temperature loading condition,which help to enhance our understanding of thermal-mechanical safety of PBXs.
2.Model descriptions
2.1.Material microstructures
A microstructure diagram of a typical PBX is plotted in Fig.1[27].The figure shows the brittle energetic crystal in PBX explosive containing microcracks with a random distribution and orientation.A microvoid in PBX can be classified as intragranular or intergranular,according to its location.
Intragranular voids refer to the void defects formed in the crystal owing to the loss of atoms,impurities,and other factors in the process of crystal growth.The number of these voids is generally small and can be regulated by improving the crystal growth process.Intergranular voids are usually distributed in the binder or binder-crystal interface and are mainly formed in the following three processes:
(1)During the pressing and molding process,due to the poor coating performance of the binder in the local area,the phenomenon of debonding occurs,i.e.,formed microvoids are due to the inhomogeneity resulted from the pouring and solidification processes.
(2)In the storage process,the aging phenomenon of explosives gradually occurs,and the volatilization loss of the internal components causes the shift of materials from their original positions,forming voids.
(3)The process of transportation and service causes interface debonding of explosives under external mechanical stimulation,thermal expansion between components under thermal stimulation,or microvoid damage after thermal decomposition reaction.
Based on these-defect distribution characteristics,two kinds of micro defects in PBX explosive in the initial state are assumed,as shown in Fig.1.Microcracks are isotropic and mainly distributed in the explosive crystal,and microvoids are mainly distributed at the interface of the binder or crystal.In the theoretical derivation of the model,the physical mechanism of the evolution of micro defects issimplified,and the interaction between the two kinds of micro defects on the mechanical behavior of materials is ignored.

Fig.1.Micrograph of PBX 9501 initial morphology[28].
The organizational framework of PBX microcrack and microvoid thermochemical coupling micromechanical model(CMM)is shown in Fig.2.The bulk stress and strain are decomposed into a deviator part and volume part,respectively,and the microcrack-related deviator constitutive relation and microvoid-related volume constitutive relationship are established in turn.The two are coupled through the Gurson model.The relevant variables are updated through the microcrack/microvoid evolution law with the friction hotspot model of vertical shear cracking.
2.2.Stress-strain formulations
Based on the theory of continuum mechanics,the total strainε is divided into deviatoric e and volumetric components ε:

where εis the plastic volumetric strain,and εis the elastic volumetric strain.Thermal strain is calculated by ε= αΔT,where αandΔT are thermal expansion coefficient and temperature variation of unit node,respectively.According to strain superposition theory[29],the total deviatoric strain e is decomposed into the viscoelastic deviatoric strain,plastic deviatoric strain,and cracking deviatoric strain,which can describe the viscoelastic deformation e,plastic deformation e,and the influence of microcrack propagation on the mechanical behavior of PBX explosive e,respectively.
The viscoelastic deformation of PBX is described by the generalized Maxwell model.The relationship between the deviatoric stress rate and the deviatoric strain of the nth Maxwell viscoelastic element in the generalized viscoelastic element is given by
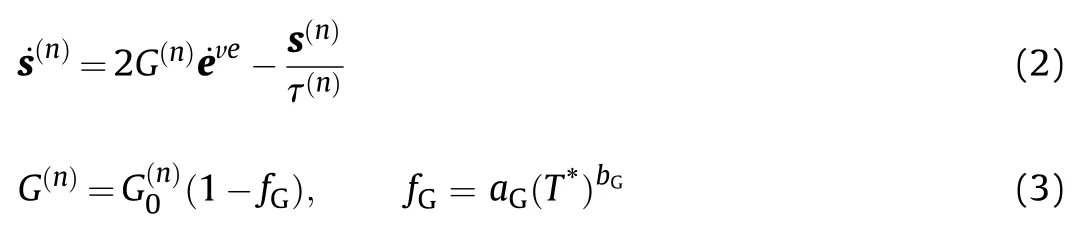
According to the parallel characteristics of the generalized viscoelastic volume element,the deviatoric stress rate is described by
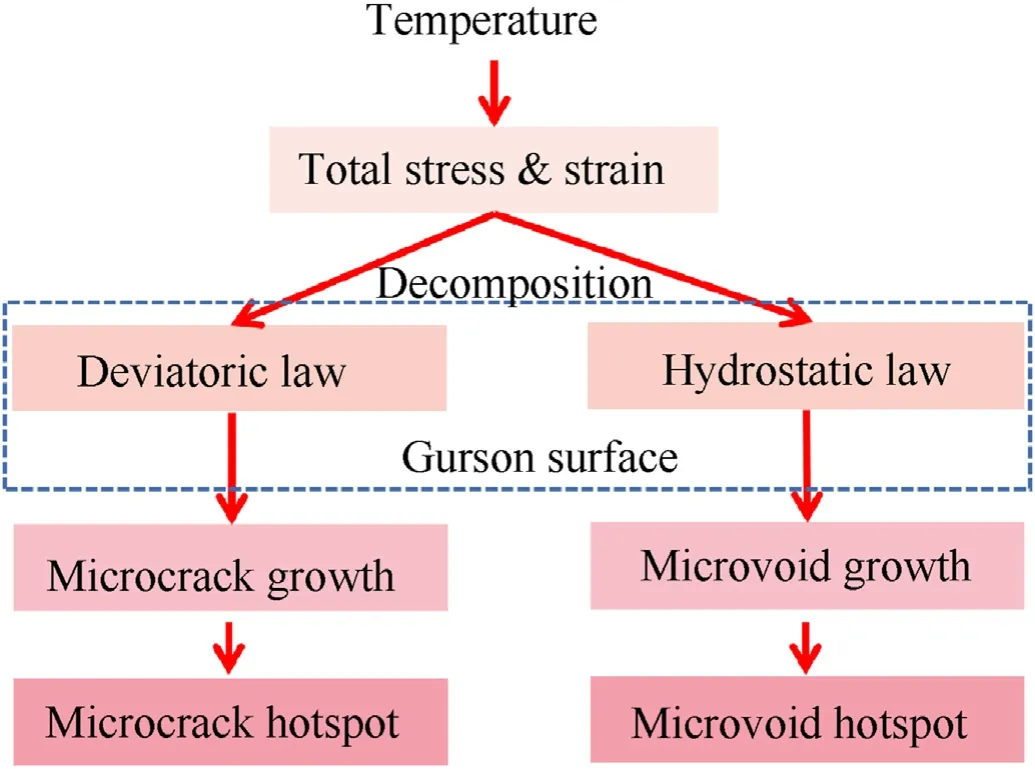
Fig.2.Organizational framework of microcrack-microvoid-related force CMM.

where N is the number of elements in the generalized Maxwell model.
The plastic deviatoric strain rate is calculated by

where the plastic multiplier˙λ is determined by the consistency condition F=˙F=0.
The deviatoric crack strain is calculated by

Multiply Eq.(6)by 2G to derive the generated equation,
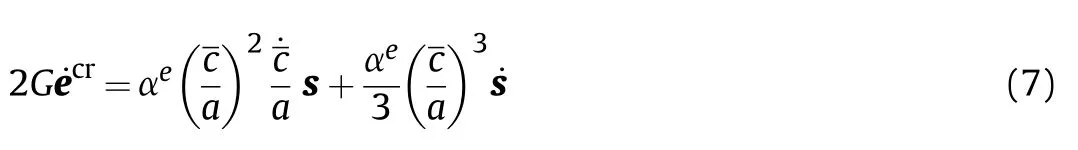
where a is the initial flaw size,which is expressed as a=6Gβ.
Integrating Eqs.(4),(5)and(7)yields
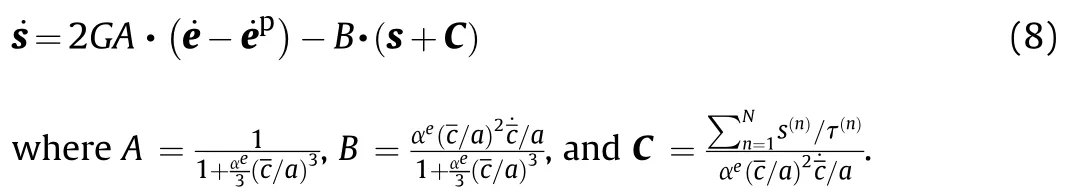
The deviatoric stress rate for the nth Maxwell element is given by
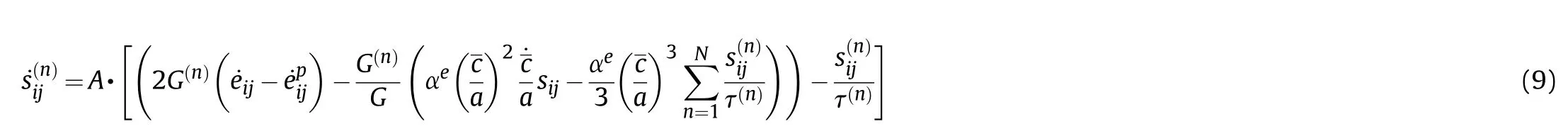
2.3.Microcrack growth model with temperature dependency
When the external stress reaches the critical value of crack growth,the microcracks begin to lose stability and grow in size.Details of the DCA model are referred to the literatures[30—32].

where L(σ,n)is expressed by
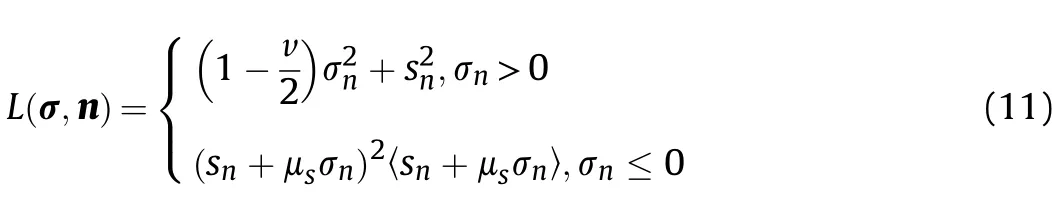
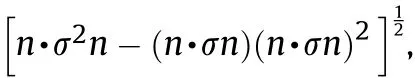

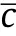
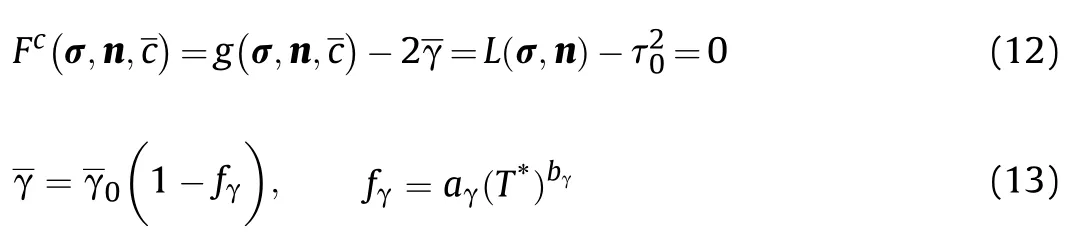
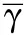

Fig.3.Schematic diagram of the failure surface of penny-shaped microcracks under the σn-sn plane.

The approximate normal direction of the crack obtained by the solution depends on the propagation form of the crack(opening,closing,shearing),and its value depends on the stress biaxiality(r=σ/σ)under the loading stress,which can be divided into five stress states.

The critical orientation(n)and energy-release rate in each crack-growth mode were studied[33].The crack growth law is defined by the Griffith instability criterion,
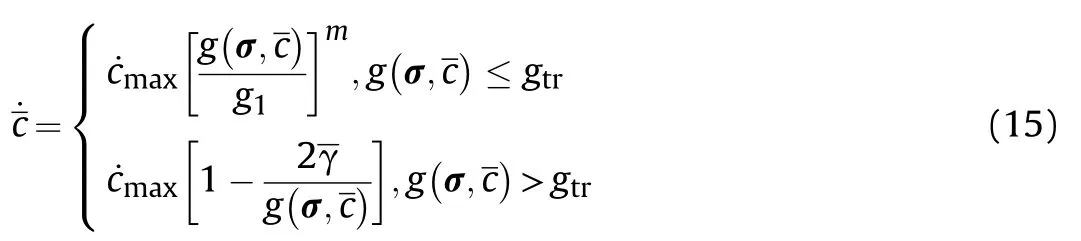
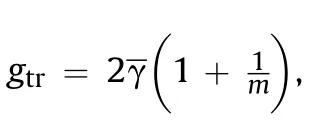
The damage fraction related to the microcrack growth can be defined as

2.4.Frictional shear-crack hotspots
Microcrack evolution not only could cause damage and failure behavior of the PBX explosive material.The heat released by the friction of the crack surface during the shear-crack propagation can also cause the formation of a local high-temperature zone(hotspot)inside the explosive,which affects ignition and subsequent combustion of explosive.In this study,a heat conduction equation is used to describe the thermodynamic processes of frictional heat generation,melting,ignition,and heat transfer on the surface of the shear crack and its surrounding area[29].
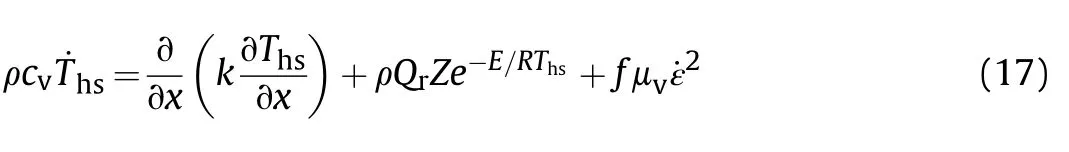
where x is the coordinate axis along the crack normal;T,c,k,and Qare the hotspot temperature,heat capacity at constant volume,thermal conductivity,and chemical heat release per unit mass,respectively;Z and E are Arrhenius reaction rate parameters;f(0≤f≤1)is the melting fraction;μ is the viscosity of the melt.The shear strain rate˙ε is calculated by˙ε=f v/l,where vis the cracksliding velocity and l is the width of the region at or above the melting point.Three terms on the right side of Eq.(17)represent conducted heat,heating resulting from the chemical reaction,andviscous heating of the melted liquid[34].
The crack-sliding velocity vis calculated by the central velocity of shear crack:
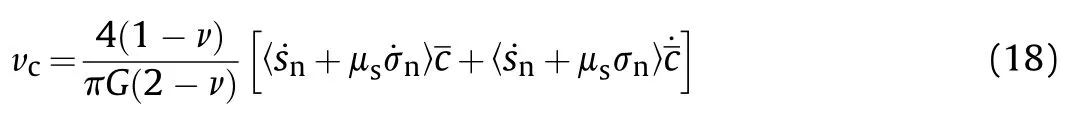
The first term of Eq.(18)represents the sliding velocity of the crack due to the change of the driving force on the surface of the microcrack,and the second term represents the sliding velocity of the microcrack caused by the propagation of the microcrack.
The frictional heat generation of microcracks per unit area can be regarded as the boundary condition of the microcrack surface(x=0):
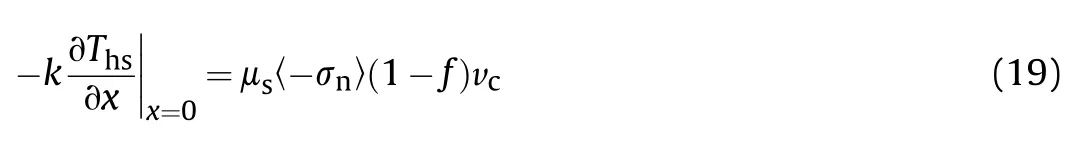
When the temperature at the crack interface reaches the melting point(T),a solid-liquid phase change is initiated.During the melting of the material(0
The melting rate is calculated by
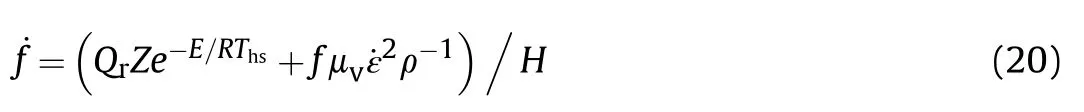
where H is the latent heat of melting.
As the melting progresses,the solid-liquid interface gradually spreads into the solid phase material.The velocity of the melting front˙l(t)is calculated by

whereΔ(kT)is the discontinuity in the heat flux across the melting front.
2.5.Calculation of bulk temperature rise
The rise rate of PBX explosive material's bulk temperature is obtained by external work,
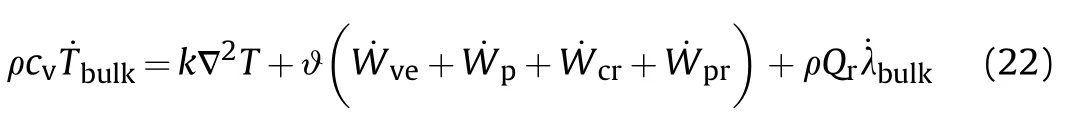
where the first term on the right side is the heat conduction of the material and˙W,˙W,and˙Wrepresent the inelastic work rates resulting from viscous effects,plastic effects,and crack damage,respectively.˙Wrepresents the adiabatic compression heating rate.The last term on the right side of Eq.(22)is the bulk chemical heating;∇is the Laplace operator;ϑ represents the fraction of the inelastic work that is converted to heat[34].
The bulk reaction of the material can be given by

The time scale of the bulk heat conduction of PBX explosive under low-velocity impact is generally larger than other time scales of heat generation rate[35];therefore,this study assumed that the overall temperature rise process of PBX is adiabatic and the effect of heat conduction is ignored.
2.6.Temperature-dependent yield surface
To describe the effect of porosity evolution on the plastic behavior of PBX materials,the classical Gurson constitutive model[36—38],which is related to the equivalent stress σand pressure P,is expressed by
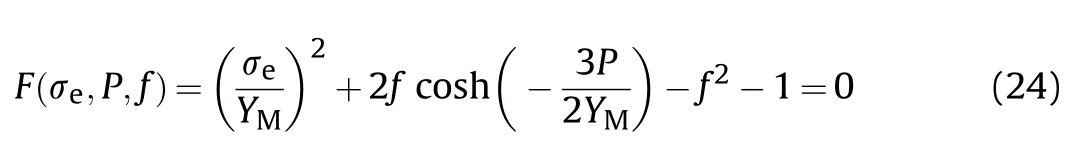
Considering the hardening response,rate dependence,and thermal effect of the solid under dynamic loading,the yield strength of the solid material is expressed by
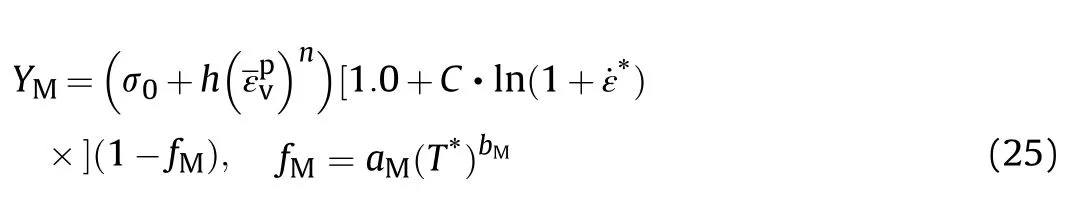
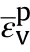
Generally,the Gurson model is used to describe the effect of void growth on the plastic deformation of materials under tensile stress(P<0),as shown in Fig.4.Yang et al.[39]explained that the Gurson yield surface(P<0)reflected along the porosity-effective stress plane(P=0)can describe the pore compression behavior under compressive stress(P>0).When f→0,the Gurson yield surface becomes the traditional von Mises yield surface.The plastic strain rate is expressed by

where˙λ is the plastic multiplier,which is determined by the consistency condition.
On the basis of Gurson's theory,the macroscopic plastic power can be expressed as
Fig.4.Schematic diagram of the yield surface of the Gurson model.

2.7.Evolution of void fraction with temperature dependency
When the PBX explosive is loaded by a high-pressure shock(high stress triaxiality),the microvoid may collapse and form a local high-temperature zone(hotspot)around the collapsed void.Additionally,when the PBX is subjected to a dominant shear load(low stress triaxiality),the microvoids inside the material will show shape deformation and orientation changes,and the interaction of adjacent voids will form a void deformation zone(void sheeting),which in turn promotes damage to the material[40—42]The hydrostatic response of porous PBXs is introduced in Appendix A.
The Gurson model,modified by Nahshon and Hutchinson[43,44],includes two deformation mechanisms:the decrease pore number caused by pore collapse and the increase in pore number caused by pore distortion,which contributes to the void growth rate for pure-shear stress states in a manner that leaves the relation unaltered for axisymmetric stress states.Based on the initial Gurson model,the revised Gurson model introduces the porosity growth rate under shear stress and the influence of temperature changes.The corresponding porosity evolution equation is expressed by

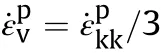

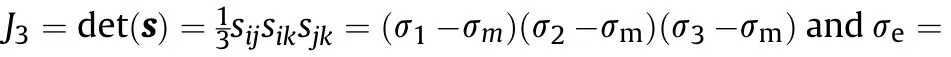
The density change rate of solid materials is
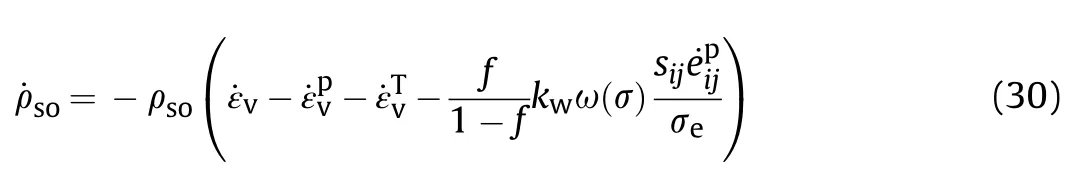
Substituting Eqs.(A5),(28),and(30)into Eq.(A3)obtains the rate of pressure:
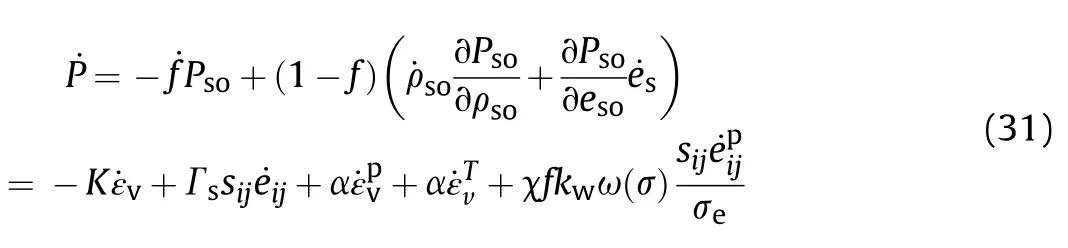
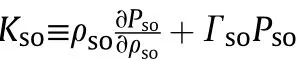
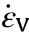
2.8.Trial-correction numerical algorithm
To solve the current modeling equations,a trial-correction timeintegration algorithm needs to be established.First,the plastic deformation of material is not considered under the current stress state.The trial deviatoric stress,hydrostatic pressure,and porosity are obtained:
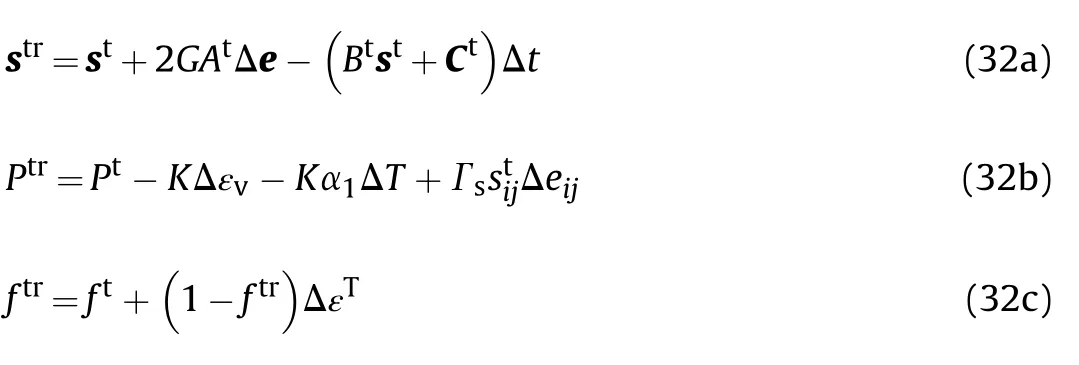
where superscripts t and t+Δt represent the start and end times of the time step,respectively,and tr corresponds to the trial calculation result.
The trial deviatoric stress for the nth Maxwell element is calculated by
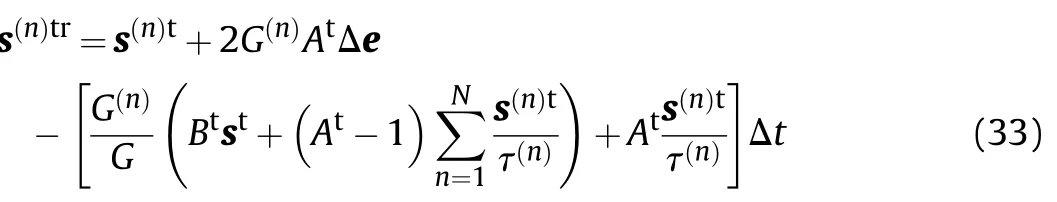
Based on the von Mises yield theory,the trial stress state of the material determines whether the material reaches the yield condition.If the material is still in the yield surface,it does not undergo plastic deformation.Currently,the trial stress state is the final update stress(final stress).If the stress exceeds the yield surface and the material is plastically deformed,the plastic strain of the material must be calculated based on the stress,and the trial stress must be corrected(corrected stress).The corrected stress is the final updated stress.
With Eq.(26)and(32a-),we can obtain

The plastic strain increment is assumed to be perpendicular to the Gurson yield surface in the stress space:

The deviatoric and bulk parts of plastic strain increment are expressed as

Applying Eq.(36a)into Eq.(34a)yields

Accordingly,the effective stress can be expressed as

Substituting Eqs.(36a)and(36b)into Eqs.(34b)and(34c)obtains
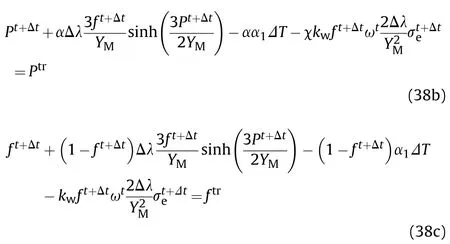
The consistency equation can be expressed as,

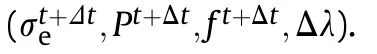
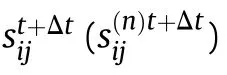

Finally,other state parameters,such as average crack size and bulk temperature rise are updated.
3.Results and discussions
3.1.Parameter determination
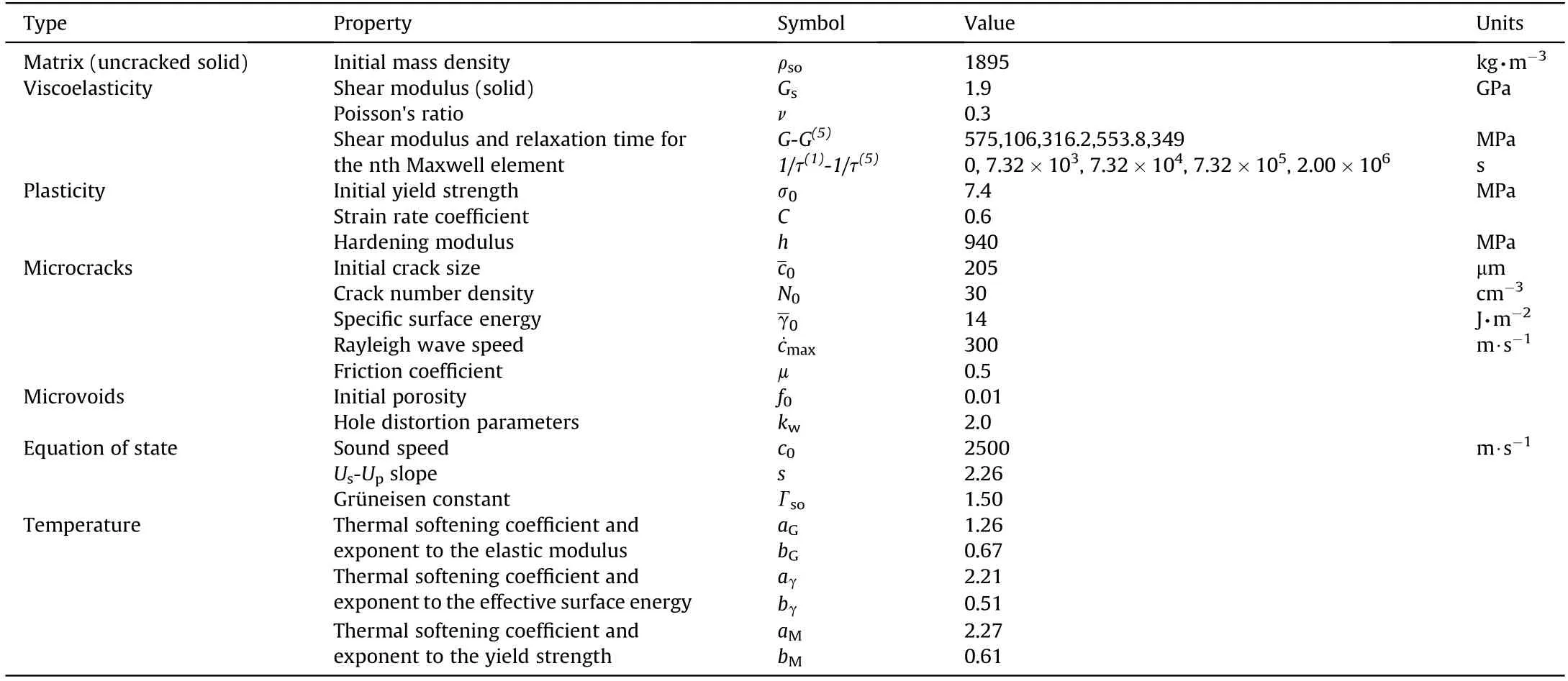
Table 1Material parameters and intrinsic model parameters of pressed PBX at 273 K.
From Fig.5(a and b),the temperature has a significant effect on the yield stress and elastic modulus of the PBXs.As the temperature rises,the yield strength and elastic modulus gradually decrease,showing an obvious thermal softening effect.Between 313 and 333 K,the thermal softening effect is more sensitive,the maximum stress decreases by 15 MPa,and the calculated results obtained using this intrinsic model are more consistent with the experimental results[46].
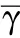
3.1.1.Evolution of void fraction
Temperature has a significant effect on the yield stress and elastic modulus of explosives.With the increase of temperature,the yield strength and elastic modulus gradually decrease,showing an obvious thermal softening effect.In addition,the void collapse rate increases significantly,and the porosity compression was 0.982% when the temperature increases to 333 K due to the softening effect of temperature.
The damage versus strain under dynamic loading conditions at different temperatures is shown in Fig.6.Under uniaxial compression,the microvoid damage reflects temperature sensitivity.The microvoid damage evolution mainly depends on the two damage mechanisms of porosity increase due to temperature rise and porosity decrease due to void collapse,and the amount of porosity change due to void distortion is negligible under uniaxial compression.
3.1.2.Microcrack-related damage evolution
Figs.7 and 8 show the crack expansion rate and damage accumulation at different initial temperatures.As the temperature increases,the crack evolution onset moment advances and the peak crack growth rate increases significantly,as shown in Fig.7.The increase in temperature causes the material to soften further,making it more susceptible to crack damage and increasing the rate of crack expansion.
3.1.3.Asymmetry in tension and compression from microcrack initiation
Fig.9(a)shows the uniaxial tensile and compressive stressstrain curves associated with the PBX damage at different strain rates.From the figure,the material exhibits a significant temperature effect with a loading strain rate of 2000 s.When the temperature increases from 273 to 333 K,the curve characteristic parameters,such as modulus of elasticity,yield strength,and peak stress,decrease.At the same time,the tensile and compressive asymmetry of the material is mainly reflected as follows.First,in the A-Bsection of the tensile curve,the elastic modulus of thematerial is weakened,and the load-bearing capacity is reduced,owing to the microcrack expansion.Subsequently,in the B-Csection,the microcrack undergoes rapid destabilization and expansion,causing the material to exhibit stress softening behavior.On the other hand,the compression curve in the A-B section first reaches the yield point D(297 K,2000 s,ε≈1.0%,σ≈18.81 MPa).Later on,the microcrack growth softening and plastic hardening together affect the mechanical behavior of the material.Secondly,the critical stress for microcrack growth in compression(A,-8.41 MPa)is about three times the critical stressfor microcrack growth in tension(A,2.86 MPa).Differences in the local stress state of the microcrack lead to different microcrack expansion patterns.Under uniaxial tensile loading(σ≥0,σ=σ=0),the microcrack growth state is mainly[I]tensile tension,and under uniaxial compression loading(σ=σ=0,0=σ),the microcrack growth state is mainly[IV]shear friction.According to the main crack expansion criterion,the critical stresses corresponding to the two microcrack expansion modes of[I]tensile stress and[IV]shear friction are,respectively,
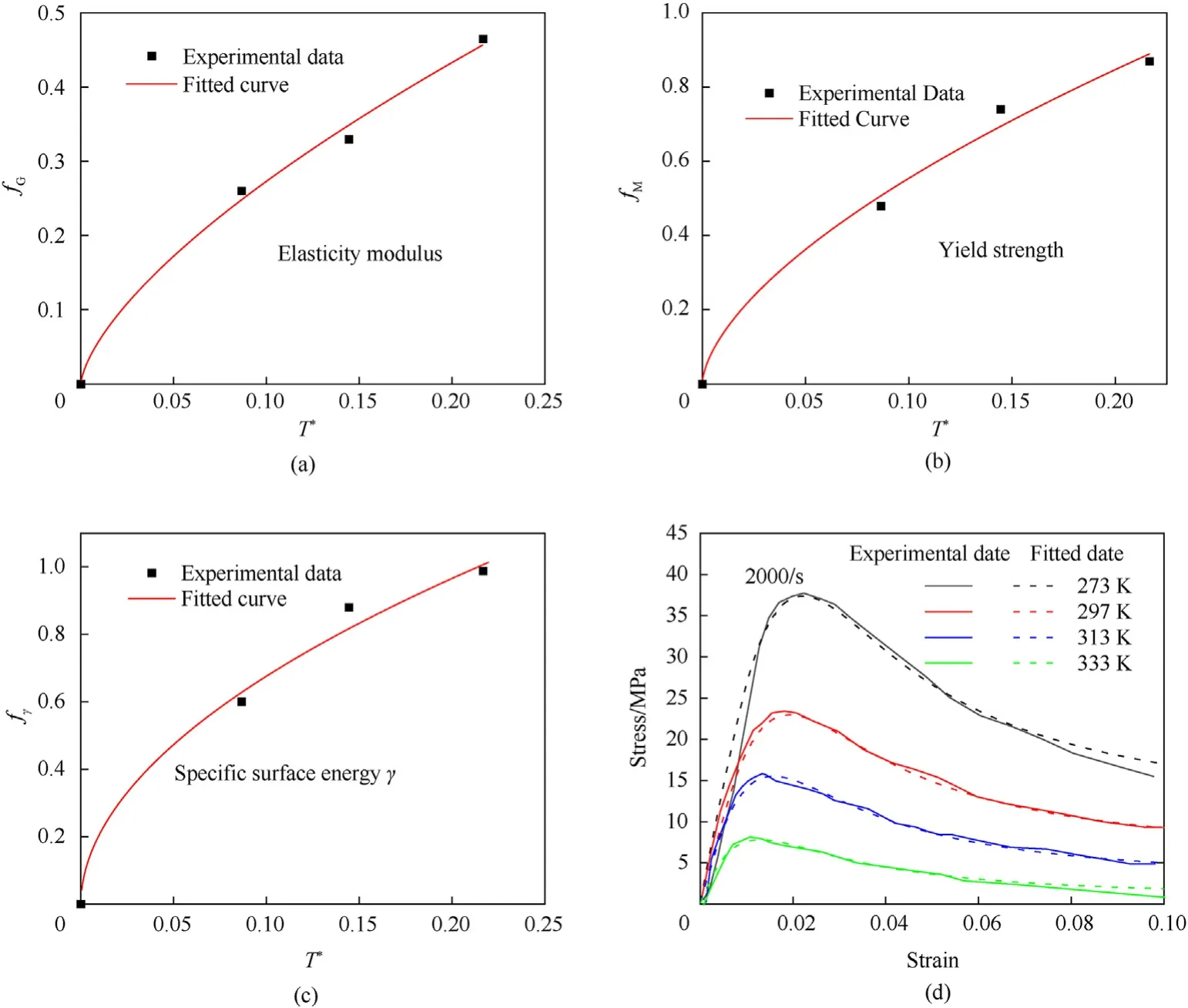
Fig.5.(a)Fitting curve of elastic modulus and temperature correlation coefficient;(b)fitting curve of modulus of yield strength and temperature correlation coefficient;(c)fitting curve of specific surface energy and temperature correlation coefficient;(d)stress-strain curves under different initial temperature conditions.
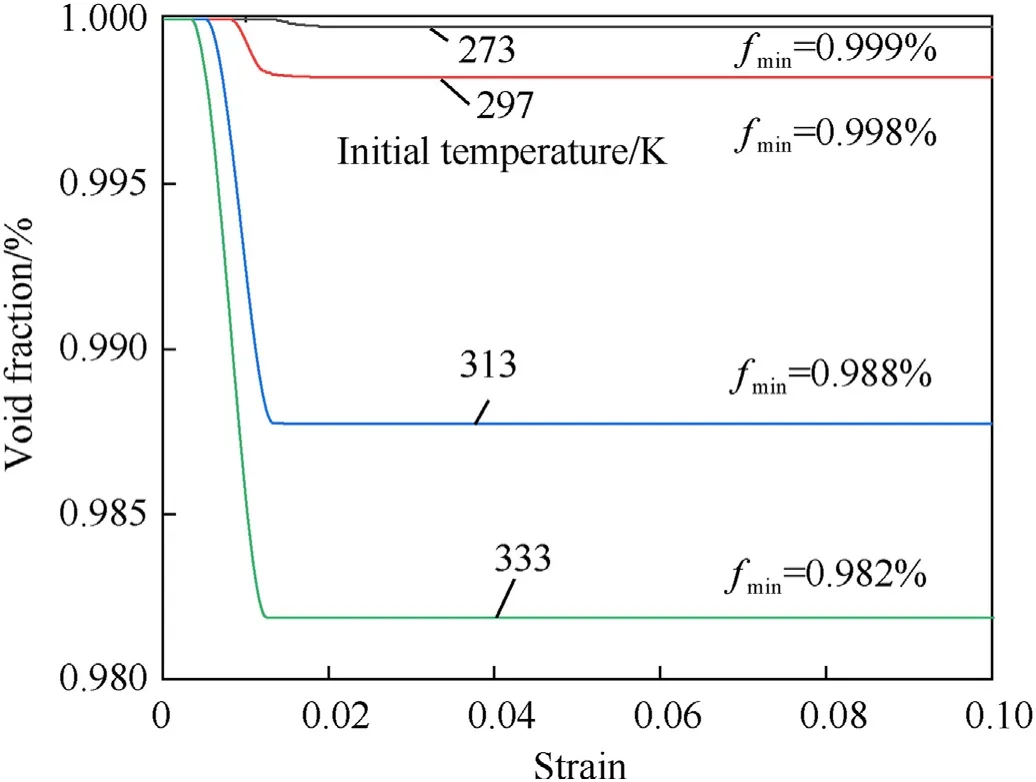
Fig.6.Porosity evolution curves for different initial temperature conditions.

Fig.7.Crack expansion rate curve at different initial temperatures.
Fig.8.Crack damage accumulation curve at different initial temperatures.
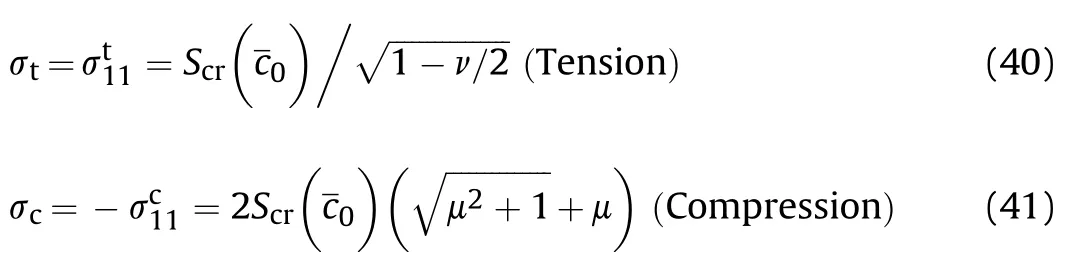
Accordingly,the two critical stress ratios can be calculated as
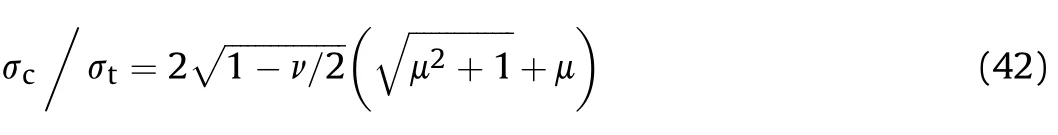
From Eq.(42),the critical stress ratio σ/σof microcrack growth under tensile loading is directly related to Poisson's ratio ν and the friction coefficient μ of the crack surface.When Poisson's ratio is constant,the increase of the friction coefficient increases the critical stress ratio,and the material will show more obvious tensilecompression asymmetry.For PBXs(μ=0.5,ν=0.3),the critical stress ratio=σ/σis 2.98[39].EDC37 is a typical pressurized explosive developed in the United Kingdom.Govier et al.[47]pointed out that EDC37 has similar mechanical properties to PBX by experimental comparison.The ratio of peak stress in the compression curve to that in the tension curve of EDC37 material is 3.10,which further verifies the mechanical behavior of the material asymmetry in tension and compression predicted by this model.
The asymmetry exhibited by microcrack growth within the PBX material under uniaxial tensile-compressive loading can be represented by the microcrack expansion rate curve,as shown in Fig.9(b).The axial strain corresponding to the occurrence of microcrack growth under uniaxial compression loading(A,0.45%)is higher than that under uniaxial tensile loading(A,0.15%).In addition,the maximum expansion velocity of shear cracks under uniaxial compression loading(B)is smaller than that under uniaxial tensile loading(B).Since the differences in microcrack expansion patterns under complex stress states are considered in this study,the current model can describe the special loading case of asymmetry exhibited by the material under uniaxial tensilecompressive loading.For more complex loading forms,such as three-way tensile-compressive loading,the current model can still describe the asymmetry in the mechanical behavior of the material due to microcrack expansion.
3.1.4.Dynamic compression with lateral confined pressure
The dependence of the PBX explosive mechanical behavior on the lateral envelope pressure is manifested in three main aspects:(i)the stress level of the PBX increases significantly with increasing lateral envelope pressure;(ii)the modulus E and yield strength σof the material increase with the increase of lateral circumferential pressure(e.g.,at 0.1 MPa,E=1.6 GPa and σ=8 MPa,and at 69 MPa,E=6—7 GPa and σ=50—60 MPa);(iii)when the lateral circumferential pressure is small(0.1 MPa),strain softening is observed in the material curve,while when the lateral circumferential pressure is large,the material exhibits a strain-hardening phenomenon.For example,in tough-—brittle transformation,the hardening modulus increases continuously with the increase of pressure.
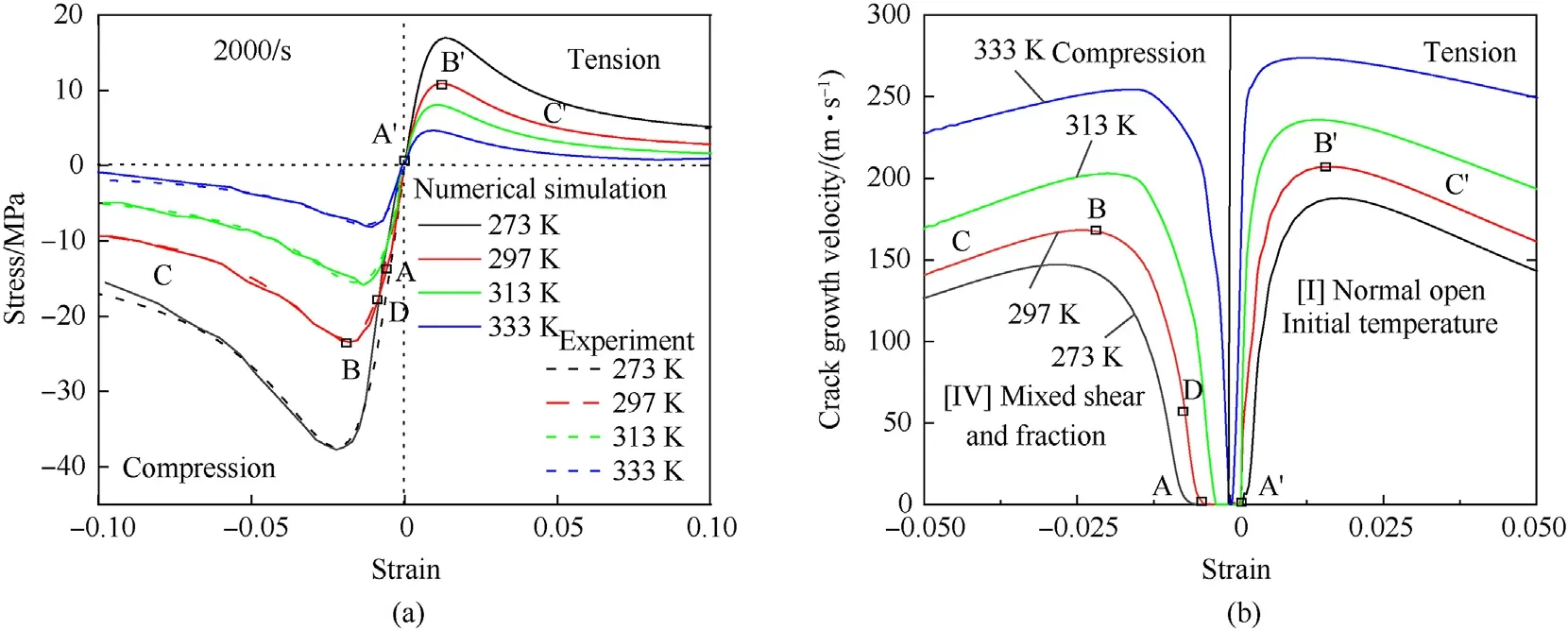
Fig.9.(a)Uniaxial tensile and compressive stress-strain curves for PBX materials at different temperatures and(b)variation curves of microcrack growth rate at 2000 s-1 strain rate.
Fig.10.Compressive stress-strain curves of PBX under different lateral confined pressure(0,0.1,50,100 MPa,2000 s-1)at(a)273 K,(b)293 K,(c)313 K,and(d)333 K.
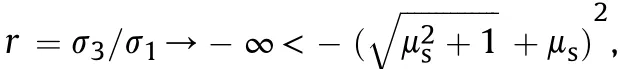
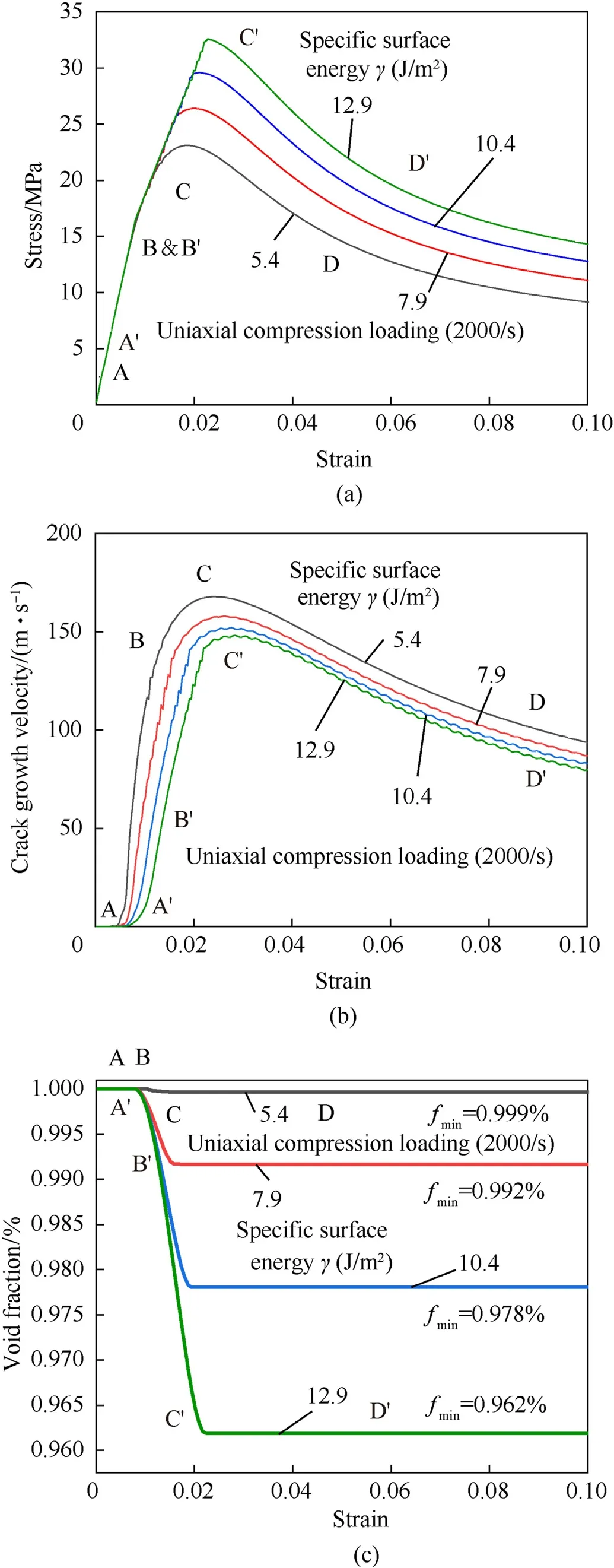
Fig.11.(a)Stress-strain curve,(b)crack growth velocity,and(c)porosity evolution curve with different specific surface energies(=0.5,0.75,1.0,1.5 J/m2)under uniaxial compression loading at 2000 s-1 strain rate.
3.1.5.Effect of specific surface energy on brittle damage
From Fig.11(b)and(c),as the specific internal energy increases from 5.4 to 12.9 J/m,the strain at the break increases from 1.9%(C)to 2.3%(C).The brittleness diminishes while the ductility increases;the stage of plastic deformation increases(BC to B'C');the porosity reductionΔf increases from 1.0×10to 3.8×10.
3.2.Damage and ignition of impacted PBXs at high-temperature
Fig.12 shows the two-dimensional axisymmetric model used in this study.The size of charged PBXs is φ50×20 mm;the thickness of the steel cover is 3.5 mm;the thickness of the steel ring that restrains the PBXs is 5 mm.These two parts combine with the steel explosive base to make up the shell that covers the explosive.The small projectile size is φ20×20 mm.The model uses a quadrilateral grid with 1501 model nodes 1322 cells,with constraints at the bottom.The top small projectile impacts the explosive at different initial velocities,and the initial temperature of the explosive before impact is homogeneous for preheating.Since ignition occurs on a time scale of less than 1 μs,heat conduction only affects a fairly small range,so the effect of heat conduction can be neglected,and the model is considered adiabatic.The explosive is loaded and unloaded within 60 μs
In order to better analyze the evolution of the state variables of the pillar during the impact,two positions,A and B,are selected for this purpose.As shown in Fig.12,position A is the center position directly below the projectile body,and position B is the intersection of the projectile body boundary and the pillar of the charge inside the shell.As shown in Fig.13,the compressional wave of approximately semicircular shape is transmitted into the interior of thesample,and the pressure and volume strain maximize at position A;and the von Mises stress is relatively small at 60 μs The von Mises stress and equivalent plastic strain are maximum at position B,and a wedge formed in the local area when the initial temperature is 348 K under 250 m/s impact velocity.When the impact velocity is high enough,the damage areas at position A and position B of the PBXs are the earliest to generate hotspots.Therefore,this section only focuses on the damage evolution and hotspot formation process at positions A and B.
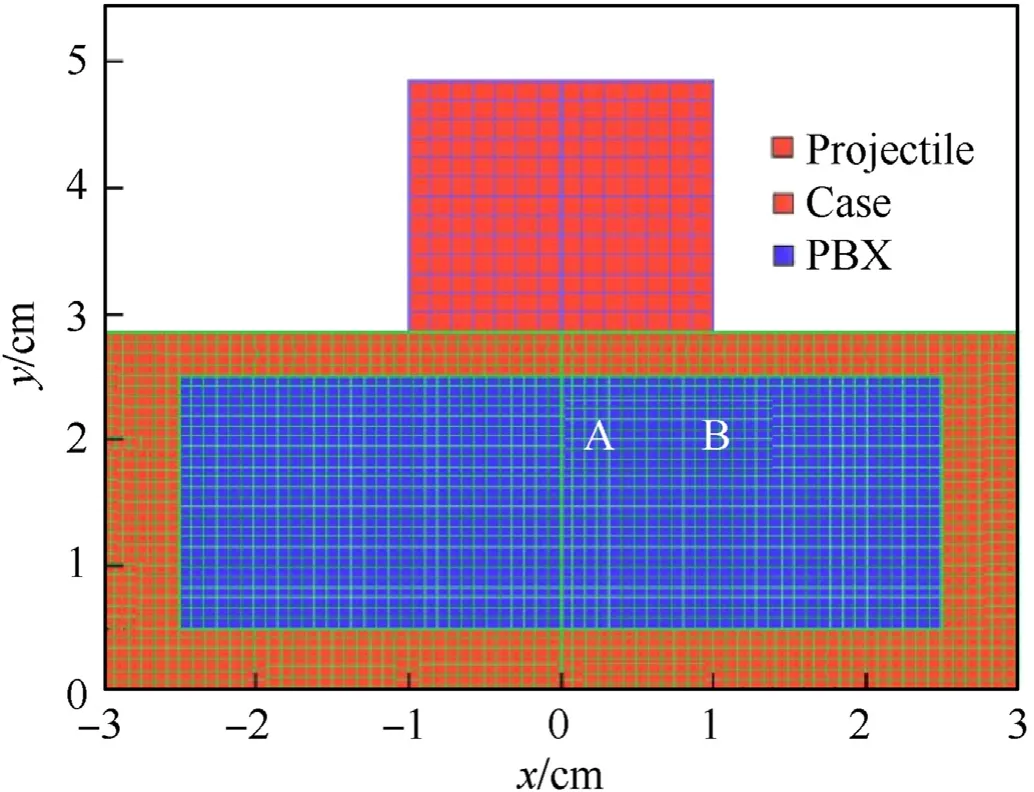
Fig.12.Two-dimensional axisymmetric finite element model and its meshing schematic.
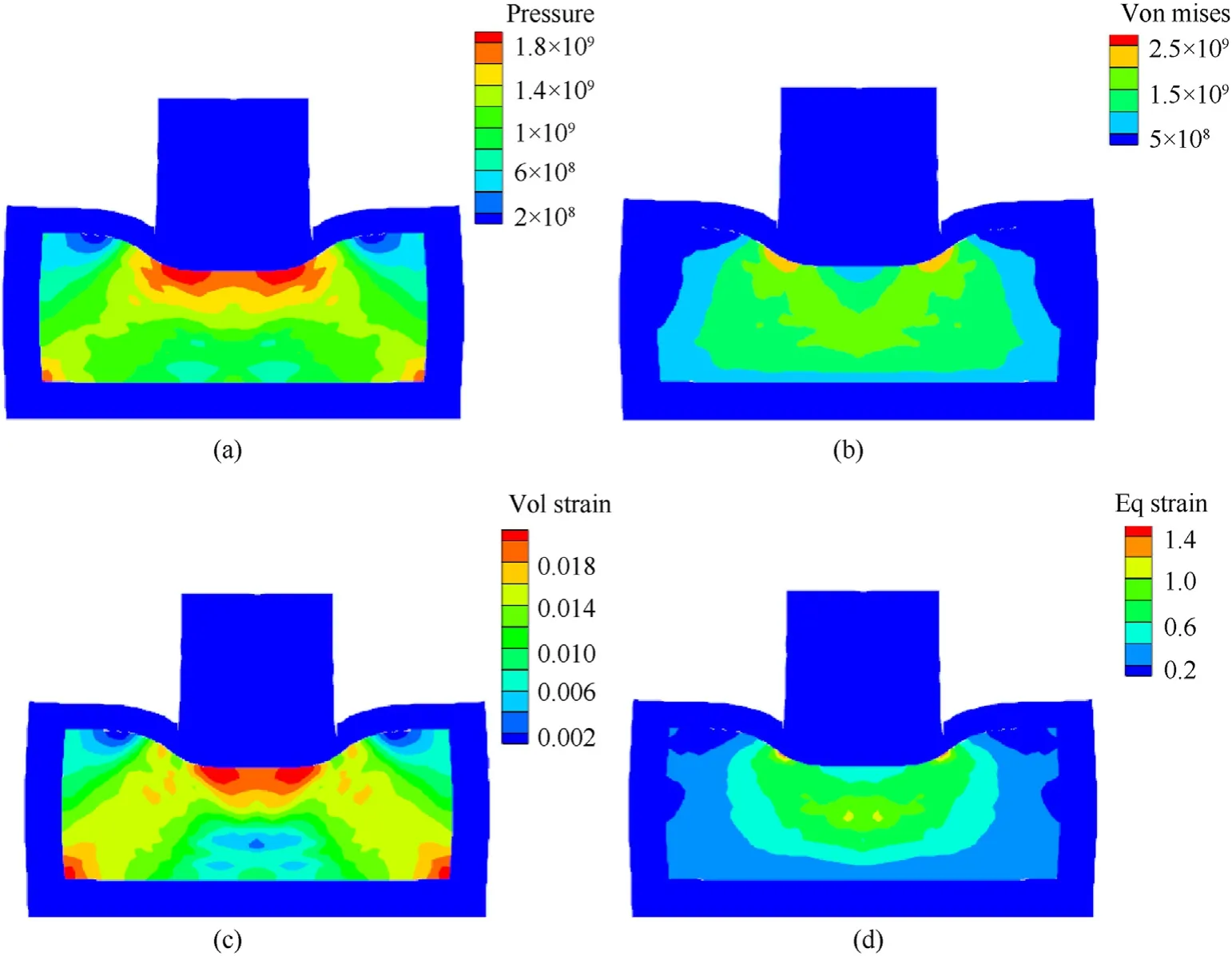
Fig.13.(a)Pressure contour,(b)volume strain contour,(c)von Mises stress contour,and(d)equivalent plastic strain contour at 348 K under 250 m/s impact velocity at 60 μs
3.2.1.Damage and heat dissipation of shear crack
3.2.1.1.Microcrack damage evolution.The impact velocity of the projectile affects the energy localization and hotspot formation of the material.Studying the ignition threshold impact velocity is essential to predict and evaluate the impact sensitivity of the explosive.Because of the stress concentration at location B,when the applied stress is large enough,the microcrack is destabilized.and the growth mode is shear friction.Since the shear friction heat generation rate positively correlates with the crack expansion rate,location B is likely to be the first to form a microcrack hotspot,which will induce an ignition response.Thus,location B is defined as a hazardous location,and the following analysis focuses on the temperature change here.
Fig.14 shows the microcrack damage evolution contours 10,20,40,and 60 μs for the initial temperature of 348 K of PBXs at 250 m/s impact velocity.The degree of material damage can be divided into four levels according to the damage percentage D:Level 1,0.3=D≤0.5;Level 2,0.5
The microcrack surface temperature histories and surrounding temperature evolution curves caused by microcracks in the B region at different impact velocities are shown in Fig.15(a and b),respectively.
After the initial impact at position B at 13 μs,the internal microcrack of the material undergoes rapid destabilization and expansion,and the frictional heat generation on the microcrack surface causes a rapid increase in its surface temperature.When the impact velocity is low(<150 m/s),the microcrack surface temperature maximizes rapidly and then decreases gradually from heat conduction.For example,at 150 m/s impact velocity,the microcrack surface temperature peaks at 412 K at 20 μs When the impact velocity increases to 250 m/s,the microcrack surface temperature increases to the melting point when a plateau is formed,which corresponds to the local melting of the material.After the complete melting of the microcrack surface occurs,the chemical reaction and the heat released from the rapid viscous flow of the liquid phase inside the microcrack cause a second increase in temperature.As the temperature continues to increase,the heat of the chemical reaction gradually dominates,and the temperature profile becomes thermally unstable,corresponding to the formation of a microcrack hotspot and reaching the critical state of ignition.From the thermal destabilization characteristics of the microcracking temperature profile in Fig.15(a),the critical impact velocity of ignition can be determined to be 320—340 m/s.
Figs.16 and 17 show the evolution of the microcrack hotspot at 250 and 340 m/s impact velocity at 348 K,respectively.The blueareas in the figures are where melting of the microcrack surface(≈519 K)is taking place,which is mainly concentrated below the impacting shell and distributed in a circular shape.The heat generated by surface friction accumulates rapidly,but the hotspot temperature stays below 750 K,and no ignition occurs.When the impact velocity reaches 340 m/s,the microcrack in the B area is subjected to high shear stress,the heat generated by surface friction accumulates rapidly to accelerate the ignition(≈750 K)process,and a wedge-shaped ignition zone is formed on both sides of the center line.
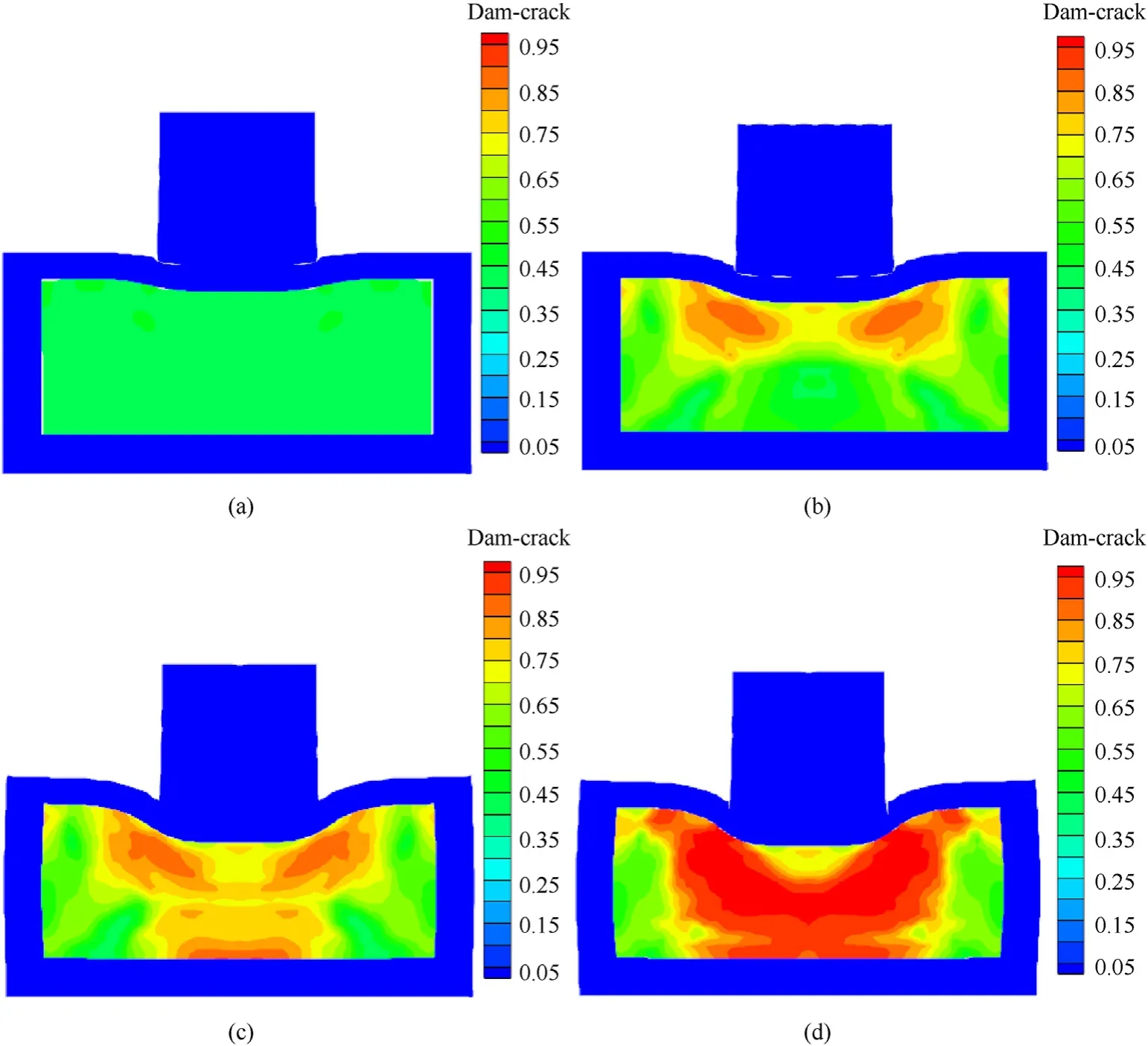
Fig.14.Microcrack damage contours at(a)10 μs,(b)20 μs,(c)40 μs,and(d)60 μs under 250 m/s impact velocity at 348 K initial temperature.
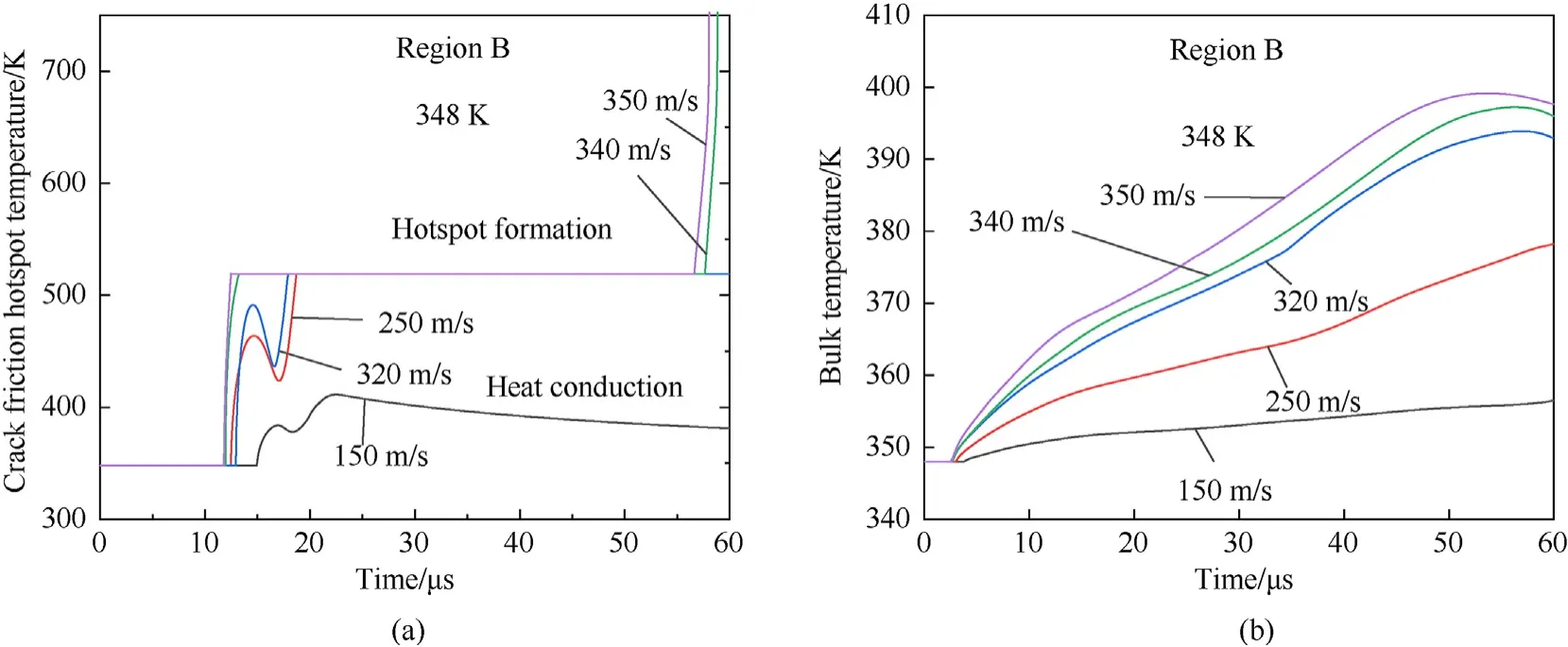
Fig.15.Temperature histories of(a)microcrack surface at position B and(b)overall temperature histories at different impact velocities at 348 K initial temperature.
3.2.1.2.Effect of initial temperature on the critical of microcrack hotspots.The effect of impact velocity on the hotspot formation process is investigated,along with the effect of different initial temperatures on the critical velocity of charge microcrack hotspot formation.As shown in Fig.18(a—c),microcrack-related hotspot temperature histories on the microcrack surface at position B under 301,348 and 378 K preheating temperatures are 260-270,315—325and 290—300 m/s for the B region,respectively.As shown in Fig.18(d),the critical velocities of numerical simulation align with the experimental data.
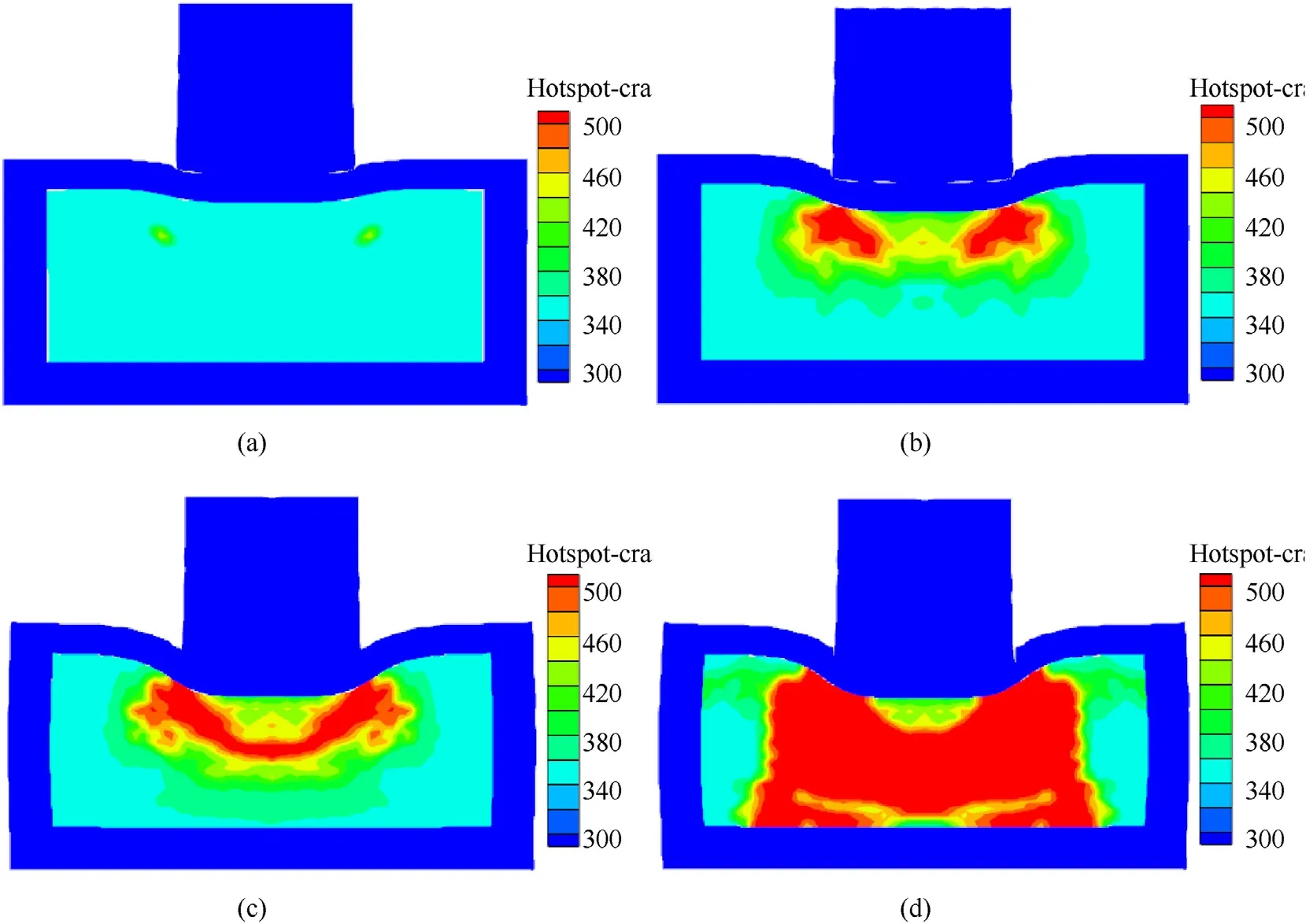
Fig.16.Contour diagrams of microcrack hotspot evolution at(a)10 μs,(b)20 μs,(c)40 μs,and(d)60 μs under 250 m/s impact velocity at 348 K initial temperature.
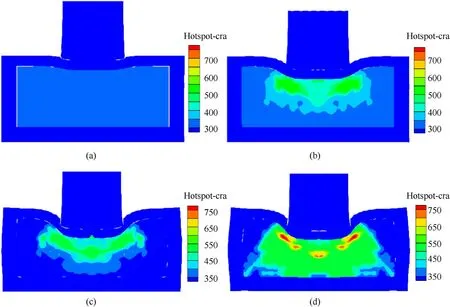
Fig.17.Contour diagrams of microcrack hotspot evolution at(a)10 μs,(b)20 μs,(c)40 μs,and(d)60 μs under 340 m/s impact velocity at 348 K initial temperature.
Fig.19 shows that as the temperature increases,a higher impact velocity is required to reach the melting temperature of the microcrack hotspot.However,when the temperature is higher than 348 K,the effect on the heat of the chemical reaction is greater,making the microcrack hotspot reach the melting temperaturemore quickly.With the increase of temperature,the critical velocity of microcrack hotspot formation gradually increases from the softening effect,and the microcrack hotspot sensitivity decreases.When the temperature rises to 378 K,the critical velocity of the crack hotspot is slightly reduced,which is consistent with the experimental phenomenon.In addition,with the increase of the impact velocity,the ignition area further expands,and a localized high-temperature zone appears in the center,still below the ignition temperature.
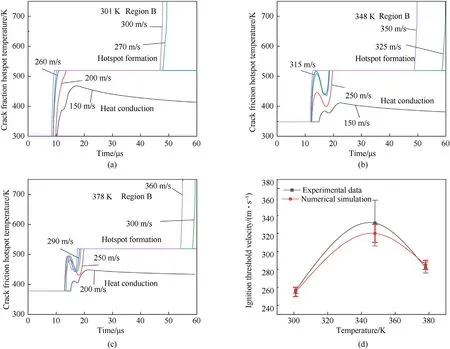
Fig.18.Microcrack-related hotspot temperature histories at location B at initial temperatures of(a)301 K,(b)348 K,and(c)378 K;(d)the critical velocities'comparison of numerical simulation results with experimental results at different temperatures.
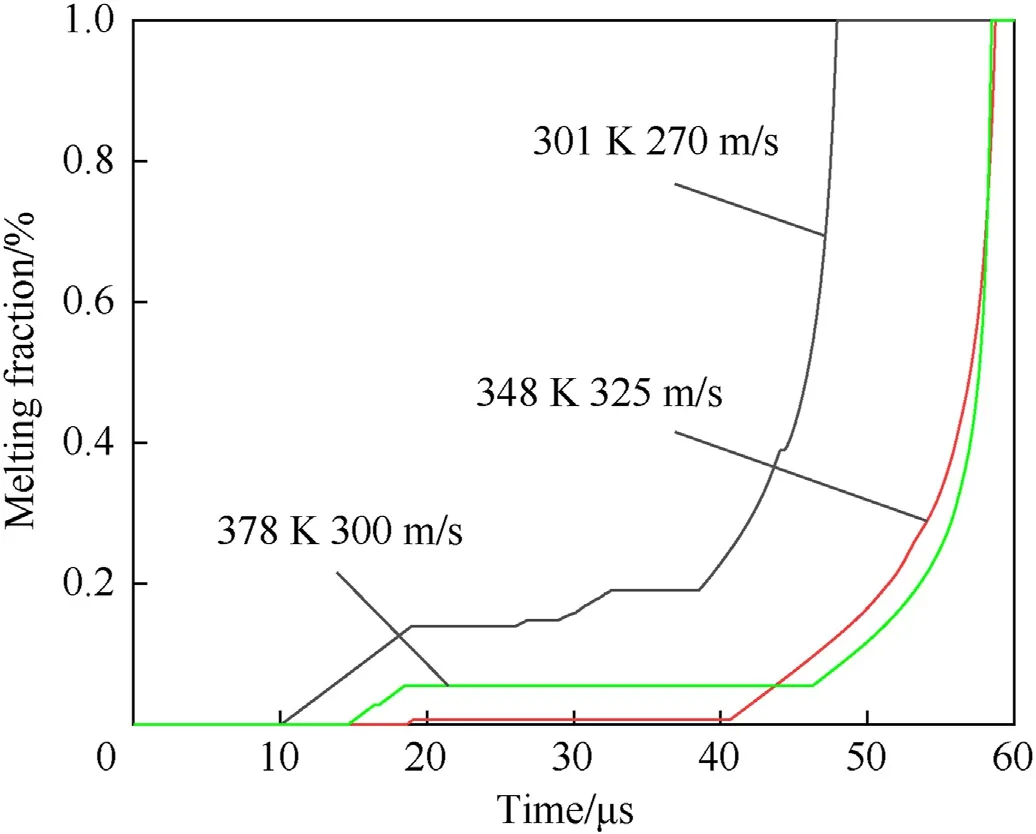
Fig.19.Melting fraction histories at different initial temperature conditions with ignition threshold speed.
The distribution and evolution of the temperature on the microcrack surface of the PBXs at an impact velocity of 420 m/s is demonstrated from Fig.20.As shown in Fig.20(a),the green region representing the region where melting(≈519 K)is occurring on the microcrack surface is mainly concentrated below the impacting projectile at 40 μs The ignition(≈750 K)starts to occur at the junction between the projectile and the PBXs(B region),and then the ignition region gradually propagates along the transition region toward the centerline,where the microcrack in the region is subjected to high shear stress and undergoes rapid shear friction expansion.The heat generated by surface friction rapidly accumulates and thus accelerates the ignition process at 50 μs
Fig.21 illustrates that when the initial temperatures are 348 and 378 K,the critical velocities of microcrack hotspot formation in the A region are 370—380 and 340—350 m/s,respectively.With the increase of initial temperature,the critical velocity of microcrack hotspot formation in the A region gradually reduces,and the diffusion velocity of the microcrack ignition zone increases further,owing to the decrease of crack initiation energy and the softening effect of temperature.
3.2.2.Formation of microvoid hotspot under punching and shearing condition
3.2.2.1.Microvoids damage evolution.When the PBX is impactloaded with high pressure,the microvoid may collapse and form a localized high-temperature zone(hotspot)around the collapsed void.In addition,when the PBX is subjected to shear-dominant loading,the microvoid within the material will exhibit shape and direction changes,and adjacent voids interact to form a voiddeformation zone,which in turn will contribute to the damage of the material.
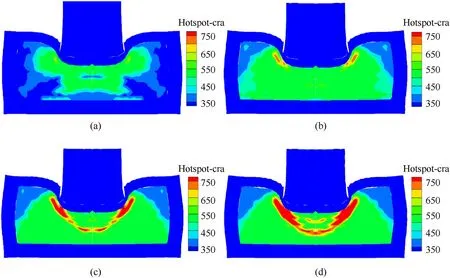
Fig.20.Contour diagrams of microcrack hotspot evolution at(a)40 μs,(b)50 μs,(c)55 μs,and(d)60 μs under 420 m/s impact velocity at 348 K initial temperature.
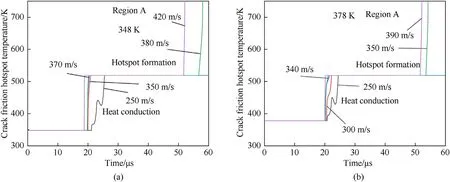
Fig.21.Temperature histories of microcrack surface at position A at different initial temperatures.
Fig.22 shows porosity evolution contours at the impact velocity of 350 m/s and initial temperature of 348 K.When the cased PBX is impacted,the microvoid damage spreads outward from the PBX and forms an elliptical region directly below the impact surface,while the region of damage is gradually transmitted into the material with the incident wavefront.As the incident wave propagates,the microvoid collapse area gradually expands to the entire charge column at 10 μs When the projectile further impacts the PBX,the void is distorted and deformed at location B of the explosive,owing to the shear stress,and the porosity is slightly higher than the rest of the explosive.After that,with the further enhancement of the incident wave intensity,the material is subjected to a pressuredominated stress state,and the material is further compacted.
3.2.2.2.Formation process of void collapse hotspot.The hotspot temperature histories caused by the collapse of microvoids in area A at 350 m/s impact velocity when the PBXs is preheated at 348 K are shown in Fig.23.The collapse of the microvoids in rigion A region causes viscoplastic deformation of the surrounding material,and its dissipative work-generated heat causes a rapid increase in the temperature profile.When the impact velocity is less than 340 m/s,heat conduction plays a dominant role in the hotspot temperature after the peak point.As the impact velocity increases to 350 m/s,the heat accumulation caused by the dissipation of viscoplastic deformation and the heat of chemical reaction are greater than the heat dissipation by heat conduction,leading to a continuous increase in the hotspot value and eventual thermal instability.
From Fig.24,the area with higher microvoid hotspot temperature(≥400 K)at 3 μs under 350 m/s impact velocity is mainly concentrated below the impact surface.With the continuous impact of the projectile,the void torsion occurs at location B because of its high shear stress state,and the microvoid hotspot temperature is gradually enhanced.With the propagation of theincident wave inside the pillar,as shown in Fig.24(d),the region with greater microvoid hotspot temperature rise at 10 μs gradually expands to an elliptical region.
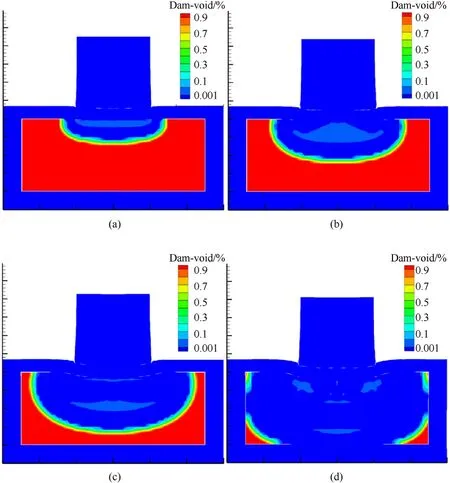
Fig.22.Porosity evolution contours at(a)3 μs,(b)5 μs,(c)7 μs,and(d)10 μs under 350 m/s impact velocity at 348 K initial temperature.
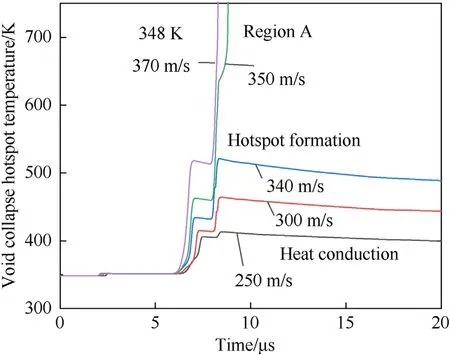
Fig.23.Temperature histories around the microvoid at 348 K initial temperature.
3.2.2.3.Effect of temperature on the critical velocity of microvoid hotspots.The effect of impact velocity on the hotspot formation process and the effect of different initial temperatures on the critical velocity of the microvoid hotspot formation in the PBXs are investigated through numerical simulation.The microcrack hotspot histories are shown in Figs.23 and 25 at 301,348 and 378 K initial temperatures at position A.The critical velocities of microcrack hotspot formation in region A are observed to be 370—380,330—340,and 290—300 m/s at 301,348,and 378 K,respectively.
The increasing temperature induces the thermal softening of PBXs.The critical velocity of the microvoids hotspot formation at position A decreases rapidly with the increase of temperature.Compared to room temperature,the effect of temperature on the critical velocity of the PBX hotspot tends to level off when the temperature is higher than 348 K.
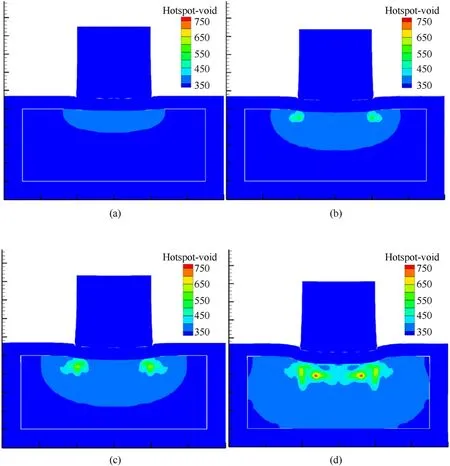
Fig.24.Temperature evolution contours around the microvoids(a)3 μs,(b)5 μs,(c)7 μs,and(d)10 μs under 350 m/s impact velocity at 348 K initial temperature.
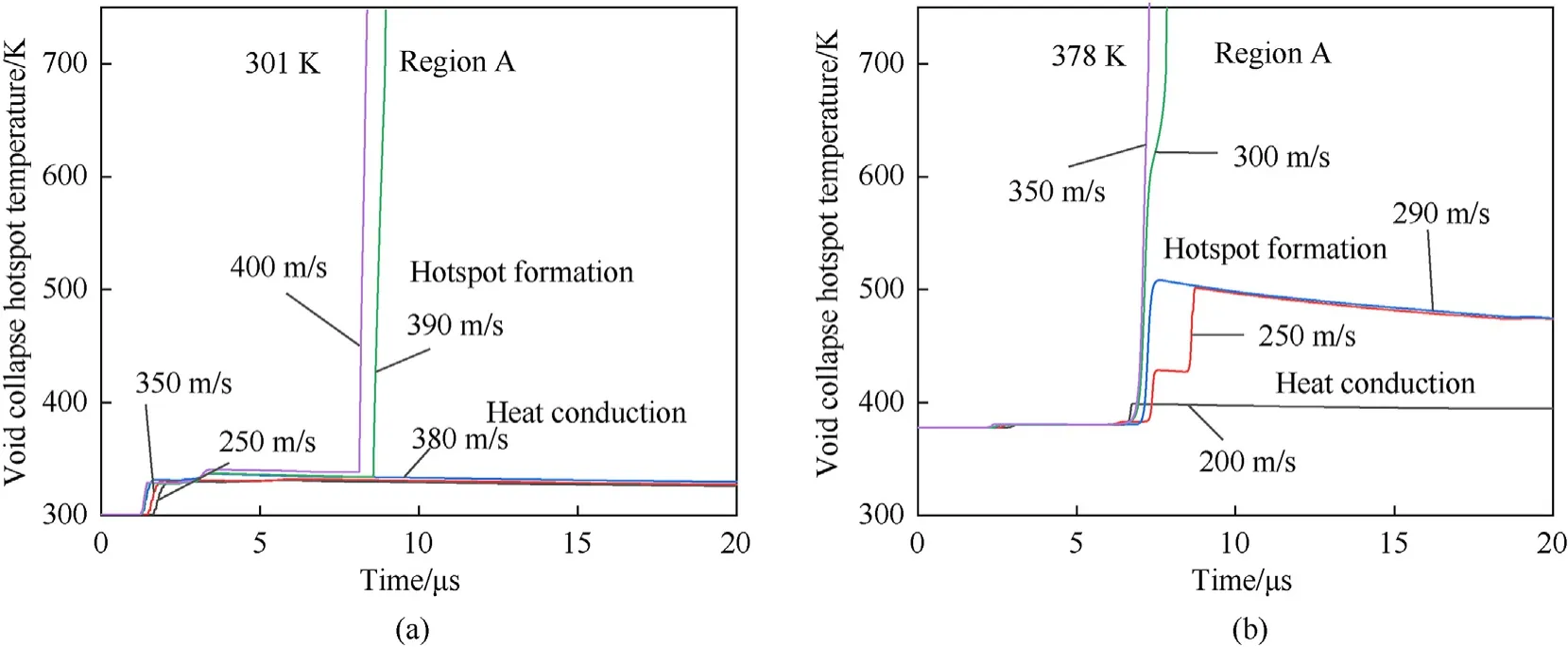
Fig.25.Temperature histories around the microvoids at position A at different initial temperatures.
4.Conclusions
To investigate the influence of temperature on impact sensitivity of PBXs at high temperature,a temperature-dependent intrinsic model of PBX explosives was developed in this paper,and numerical simulations were performed for low-velocity impact experiments of PBX explosives at different initial temperatures.The temperature effect on microcrack and microvoid ignition threshold velocities were obtained by comparing the simulation results of different impact velocities.The thermodynamic response of theexplosives was analyzed by assessing the effect of temperature on the safety of the explosives.The effect was based on the ignition threshold velocities at different initial temperatures and the location where the damage first ignition occurs.The calculation results showed the following:
·The critical speed of the ignition of the PBX microcrack and the initial temperature are not directly related to temperature.The critical velocity of hotspot formation around the microcrack increases with the increase of initial temperature.When the temperature is higher than 348 K,the critical velocity of the microcrack hotspot at position A drops slightly with the further decrease of crack initiation energy,which is consistent with the experimental data.
·The initial damage domain of the microcrack is located at two locations at the intersection of the projectile boundary and the PBX column inside the shell.However,with the propagation of the incident wave within the explosive,the respective damage domains keep expanding.As the temperature rises,the microcrack hotspot ignition area extends further down the striking column.
·With the increase of the initial temperature of the explosive,the critical velocity of the formation of microvoid hotspot decreases rapidly with the increase of temperature,and the critical velocity gradually stabilizes when the temperature is higher than 348 K,which is consistent with the test phenomenon.The initial damage domains of microvoid and microcrack are different.When the impact velocity is low,two kinds of damage locations may appear simultaneously at the center of the upper surface of the PBXs and where the boundary of the projectile meets the pillar inside the shell.However,as the incident wave propagates within the PBXs,the respective damage domains continue to expand.When the velocity is high enough,two types of hotspots may form simultaneously at the same location.
·After heating,the modulus of elasticity and yield strength of the explosive are significantly reduced,and the softening effect of temperature on the explosive causes the evolution of microcrack damage to produces the non-monotonous pattern.This shows that thermal softening plays a vital role in impact sensitivity.
Further studies of the temperature effect on composite damage should be carried out to build and investigate the effects of applying damage at a wide temperature range as a way to determining the type of resulting damage—distributed void,crack nucleation,and growth.The results obtained can be used to predict the safety of PBXs in a thermal-impact—combined environment at a wide temperature range.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
The authors would like to thank the China National Nature Science Foundation(Grant no.11872119),China Postdoctoral Science Foundation(BX20200046,2020M680394),and Pre-research Project of Armament(6142A03202002)for supporting this project.
To describe the irreversible damage produced at low pressures compression,a porosity-dependent equation of state for porous PBXs,which is on the basis of the method of Herrmann[48].Establish the relationship between the pressure of the pore PBXs and the pressure of the dense solid(the porosity is 0)as follows,

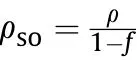
The above formula ignores the influence of the surface energy of the porous material on the internal energy.And the pressurevolume deformation relationship of dense materials is described by the Mie-Grüneisen equation of state by,

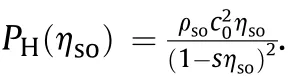
The rate of pressure is calculated by,

According to the law of conservation of mass,the density change rate of porous materials can be expressed as,

without considering the heat flux and heat sources,the rate of change of specific heat energy with time is expressed by the first law of thermodynamics,
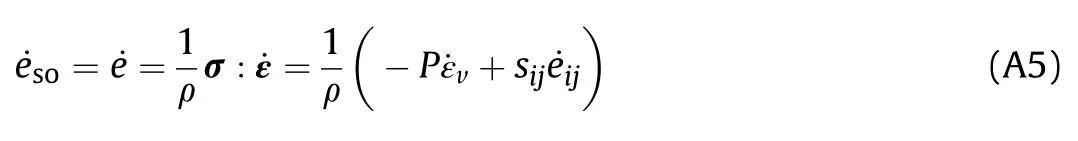
杂志排行
Defence Technology的其它文章
- 3D laser scanning strategy based on cascaded deep neural network
- Damage analysis of POZD coated square reinforced concrete slab under contact blast
- Autonomous maneuver decision-making for a UCAV in short-range aerial combat based on an MS-DDQN algorithm
- The properties of Sn—Zn—Al—La fusible alloy for mitigation devices of solid propellant rocket motors
- The surface activation of boron to improve ignition and combustion characteristic
- Numerical investigation on free air blast loads generated from centerinitiated cylindrical charges with varied aspect ratio in arbitrary orientation
