Numerical investigation on free air blast loads generated from centerinitiated cylindrical charges with varied aspect ratio in arbitrary orientation
2022-09-22ChuGoXingzhenKongQinFngJinHongYinWng
Chu Go ,Xing-zhen Kong ,Qin Fng ,Jin Hong ,Yin Wng
a State Key Laboratory of Disaster Prevention & Mitigation of Explosion & Impact,Army Engineering University of PLA,Jiangsu,Nanjing,210007,China
b Inner Mongolia University of Finance and Economics,Inner Mongolia,Hohhot,010070,China
c Engineering Research Center for Safety and Protection of Explosion & Impact of Ministry of Education,Southeast University,Jiangsu,Nanjing,211189,China
Keywords:Cylindrical charge Blast loads Aspect ratio Azimuth angle Bridge wave
ABSTRACT In current guidelines,the free air blast loads(overpressure and impulse)are determined by spherical charges,although most of ordnance devices are more nearly cylindrical than spherical in geometry.This may result in a great underestimation of blast loads in the near field and lead to an unsafe design.However,there is still a lack of systematic quantitative analysis of the blast loads generated from cylindrical charges.In this study,a numerical model is developed by using the hydrocode AUTODYN to investigate the influences of aspect ratio and orientation on the free air blast loads generated from center-initiated cylindrical charges.This is done by examining the pressure contours,the peak overpressures and impulses for various aspect ratios ranged from 1 to 8 and arbitrary orientation monitored along every azimuth angle with an interval of 5°.To characterize the distribution patterns of blast loads,three regions,i.e.,the axial region,the vertex region and the radial region are identified,and the propagation of blast waves in each region is analyzed in detail.The complexity of blast loads of cylindrical charges is found to result from the bridge wave and its interaction with primary waves.Several empirical formulas are presented based on curve-fitting the numerical data,including the orientation where the maximum peak overpressure emerges,the critical scaled distance beyond which the charge shape effect could be neglected and blast loads with varied aspect ratio in arbitrary orientation,all of which are useful for blast-resistant design.
1.Introduction
Deliberated and occasional explosions increasingly occur in recent years.The blast loads(overpressure and impulse)induced by various charges may cause a direct devastating damage to buildings,devices,and human beings.In current guidelines such as the UFC-3-340-02[1],blast loads are mainly determined based on the empirical formulas proposed by Kingery and Bulmash[2],in which a spherical charge for free air bursts or a hemispherical charge for surface bursts is assumed.However,most of ordnance devices are more nearly cylindrical than spherical(hemispherical)in geometry[3].For a cylindrical charge,the shock wave will not enter the surrounding air as a spherical wave,nor at the same instant over the entire charge surface.Consequently,the shape and amplitude of shock wave entering the air will depend on the charge geometry(aspect ratio)and the relative location to the charge(charge orientation)[4],also known as the so-called charge shape effect.Previous studies[5—7]have demonstrated that the neglect of charge shape effect may unavoidably result in a great underestimation of peak overpressure and impulse in the near field,leading to an unsafe design of structural components.
The effect of charge shape on blast loads are noted as early as 1948,when Stoner and Bleakney[8]measured the peak overpressures from spherical,cylindrical and rectangular charges(TNTand pentolite),respectively.Wisotski and Snyer[9]experimentally investigated free air bursts generated by end-detonated cylindrical Composition B charges with aspect ratio(length to diameter,L/D)ranged from 1/4 to 10 and varied charge orientation.The experimental data demonstrated that the blast loads generated by cylindrical charges were far different from those by spherical charges.A series experiments on free air bursts by cylindrical charges were later conducted by Ismail and Murray[10],and it was found that the blast wave patterns were very complex and the pressure-time histories exhibit multiple shocks,which mainly results from the overlap and interaction in the process of wave propagation.The overpressure and impulse generated from the center-initiated cylindrical charges(TNT and C4)were successfully measured by Simoens and Lefebvre[11].The peak overpressure(impulse)along the radial direction with an aspect ratio of 4 could be 1.8(1.4)times of those from corresponding spherical charges,and this increased effect existed in a relatively wide range of the scaled distance before it vanished.The experimental investigations mentioned above have demonstrated that the charge shape effect cannot be neglected for determination of blast loads.However,little quantitative information is available,which is mainly attributed to the lack of accurate measurement of the blast loads,especially in the near field.With the rapid development of computer power,numerical simulation plays an increasingly important role in development of guidance for blast-resistant design[12].The numerical simulation can provide detailed information that cannot be directly obtained in the high-risk and expensive blast experiments.Validated numerical simulations have been successfully used in the determination of blast loads,e.g.,the reflected overpressure and impulse on the chamber wall for a cylindrical charge[13],and the generated pressure waves by various-shaped charges[14].
Since the blast wave does not propagate spherically for the cylindrical charge,the blast loads at specified charge orientation should be quantified[9,15].An experimental investigation on overpressures and impulses acting on a flat target generated from spherical and cylindrical charges was conducted by Wu et al.[16].The test data showed that for a large value of aspect ratio,most of the explosive energy is focused in the radial direction whereas for a small aspect ratio,most of the explosive energy is focused in the axial direction.The experiments on free air bursts by Johnson et al.[17]using cylindrical charges confirmed that locations of the greatest pressure in the near field corresponded to the regions with the highest presented area.It is noted that the experimental studies above cannot provide the distribution of blast loads of cylindrical charges in arbitrary orientation.Recently,the distribution of blast loads for cylindrical charges was numerically investigated by Xiao et al.[7],which was done by recording the overpressure and impulse at several certain scaled distances with an 11.25interval of azimuth angle defined as the angle between the longitudinal axis and the axis of measurement.It was found that the maximum peak overpressure and impulse did not always emerge along the axial or radial direction,which can be attributed to the presence of the bridge wave(will be discussed in detail in Section 3.1).Note that there indeed exists a critical scaled distance beyond which the shock waves approximately heal into a spherical wave,and consequently,the charge shape effect could be neglected and the blast loads can be determined by those generated from a spherical charge with equal mass.This critical scaled distance was numerically determined by Sherkar et al.[12]on the condition that blast loads along the axial and radial directions approximately equal to those by corresponding spherical charge(within a deviation of 10%).However,as pointed out by Xiao et al.[7],the maximum blast loads do not always occur along the axial and radial directions,and consequently,blast loads along other directions are needed to determine the critical scaled distance.Furthermore,simple formulas for the critical scaled distance and the orientation where the maximum blast loads occur at a given scaled distance,which are important for blast-resistant design and convenient for engineering use,are not yet established.
Previous studies have shown it is possible to establish empirical formulas for the free air blast loads generated from cylindrical charges[18—24].Generally,the blast loads should be dependent on the aspect ratio,the scaled distance and the azimuth angle.For the peak overpressure,based on curve-fitting the experimental data by Wisotski and Snyer[9],Plooster[18]presented an empirical formula for the primary peak overpressure in directions of cylindrical charges with a 22.5interval of azimuth angle,but the valid scaled distance(≥2.16 m/kg)is limited.USDOD[19]developed an empirical formula for the peak overpressure along the radial direction but other directions were not considered,while Knock et al.[20,21]presented formulas for both the axial and radial directions.As for the impulse of cylindrical charges,based on the analysis of peak overpressure data and Brinkley-Kirkwood theory[25],quantitative estimation of impulse was conducted by Plooster and Yatteau[22],but it is not entirely successful due to the lack of an adequate set of experimental impulse data for comparison with the theory,as noted by the authors.Simple formulas as a function of charge mass and scaled distance for the impulses along the axial and radial directions were presented by Knock et al.[20,23],and the impulse along radial direction was considered to be independent of the aspect ratio[24].Well-established empirical formulas for the blast loads generated from cylindrical charges with detailed considerations of the aspect ratio,scaled distance and azimuth angle,which are very convenient for engineering use,are so far unavailable.
In summary,there is still a lack of systematic quantitative analysis of the blast loads generated from cylindrical charges,which in turn impedes the establishment of empirical formulas for the characteristics of blast loads,e.g.,critical scaled distance,peak overpressure and impulse,all of which are important for blastresistant design.A numerical investigation on free air blast loads generated from center-initiated cylindrical charges is conducted in the present study.This involves identifying the influences of aspect ratio and orientation on the blast loads based on a detailed analysis of the numerical results,and then establishing corresponding empirical formulas.The numerical model is developed in Section 2,which is then used to investigate the distributions of peak overpressure and impulse with varied aspect ratio in arbitrary orientation in Section 3.The corresponding empirical formulas for the peak overpressure and impulse are presented in Section 4,which is followed by conclusive remark in Section 5.
2.Numerical model
This section describes the numerical model employed to calculate the free air blast loads(overpressure and impulse)of spherical and cylindrical charges.Numerical simulations are conducted with the hydrocode AUTODYN.AUTODYN employs a singlematerial high-resolution Euler flux-corrected transport processor for blast problems[26]and includes a remapping strategy in which the output of a high-resolution detonation stage is remapped as initial conditions for a subsequent calculation stage,enabling efficient and accurate modeling[27].
2.1.Geometry,boundary condition and material models
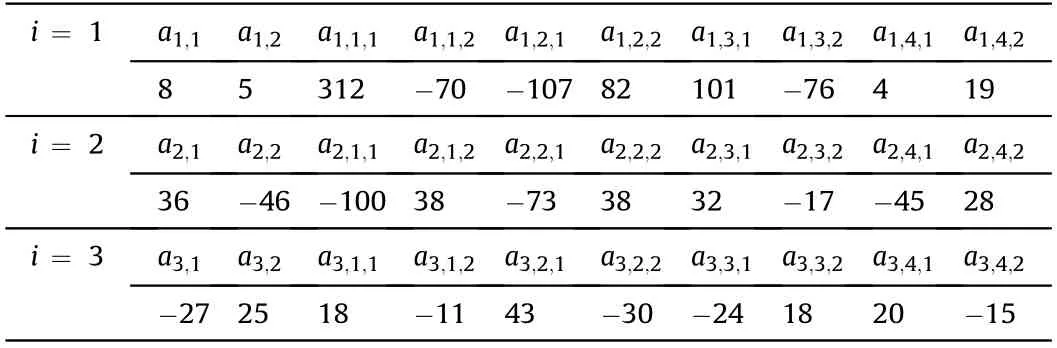
For simplicity,a 1 kg-TNT with different shapes is employed to investigate the distribution of blast loads.For a comparison purpose,a spherical charge with a diameter of 105.4 mm and density of 1630 kg/mis used as a baseline.The geometries of cylindricalcharges with varied aspect ratio can be determined by holding the mass as constant,as shown in Table 1.Note that the maximum aspect ratio is considered as 8 to cover most of ordnance devices.All charges are assumed to be detonated at their geometric center(center-initiated).
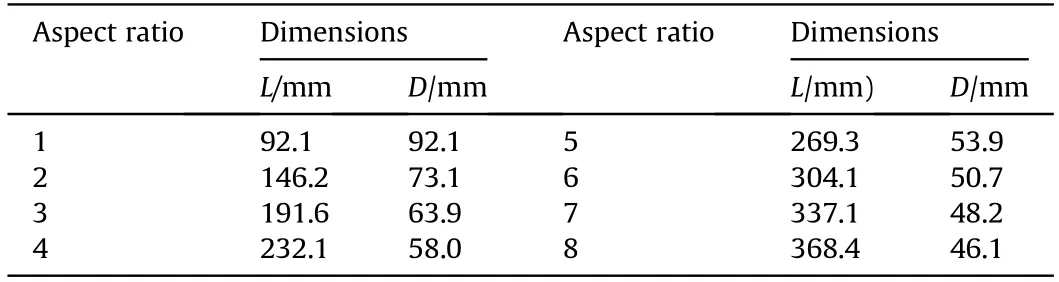
Table 1Dimensions of cylindrical charges with a constant mass of 1 kg.
To save computational cost,the 2D axisymmetric finite element(FE)model is used.Furthermore,only half of axisymmetric charge and air domain is needed to be modelled due to the central detonation.The detailed FE model and boundary condition are shown in Fig.1,where x=0 represents the mirrored-symmetric plane and y=0 represents the axisymmetric plane and the flow-out boundaries are applied to other planes to ensure the free air bursts.
The so-called remapping strategy[27]in the AUTODYN is adopted.In this strategy,numerical simulations are performed in two stages.As shown in Fig.2,the first stage associated with the initial charge expansion is conducted until shock front reaches a distance as three times of charge diameter(corresponding to a scaled distance of 0.316 m/kg),in which the air domain is considered as 0.4 m×0.4 m.This ensures the transformation of equation of state of TNT from Jones-Wilkens-Lee(JWL)to ideal gas automatically[26].Then the output of first stage is remapped into an air domain 10.0 m×10.0 m(corresponding to a maximum scaled distance of 10 m/kg),and the analysis is conducted until the expected calculation time.This strategy allows the use of a finer mesh at the first stage and a coarser mesh at the second stage,which enables the accurate and efficient modeling.
Both the air and TNT are modelled by Euler grid.An ideal gas equation of state is used for the air,which defines the pressure p as,

where γ=1.4 is the heat specific ratio,ρ=1.225 kg/mis the density and e=2.068×10kJ/kg is the specific internal energy.The TNT is modelled by the JWL equation of state,i.e.,
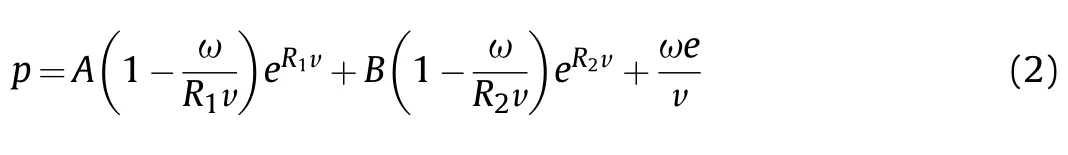
where v is specific volume,A,B,R,Rand ω are constants determined as 3.7377×10kPa,3.7471×10kPa,4.15,0.9 and 0.35,respectively.
In order to obtain blast loads in arbitrary orientation,the azimuth angles with an interval of 5are used,as shown in Fig.3,where the axial direction and radial direction of cylindrical charge are defined as 0and 90,respectively.The scaled distance Z is given as R/M,where R is the standoff distance from the charge center to the gauge and M is the charge mass.The overpressures and impulses along every azimuth angle(gauge line)are monitored at the scaled distances varying from 0.3 m/kgto 10.0 m/kgwith a minimum interval of 0.1 m/kg.Therefore,there is total number of 646 gauges for each numerical simulation.
2.2.Mesh-size convergence
Mesh-size sensitivity should be conducted to ensure reliablenumerical simulation.This is done by comparing the numerical predictions of spherical charge using different mesh sizes for both the first stage and the second stage mentioned above.For the first stage,Fig.4 shows the numerically predicted overpressure-time histories at the scaled distance of 0.316 m/kgby mesh sizes of 0.5 mm,1.0 mm,2.0 mm and 4.0 mm.It is observed that numerical predictions using the mesh sizes of 0.5 mm and 1.0 mm are almost identical.Therefore,the mesh size of 0.5 mm is chosen to guarantee the accuracy of subsequently second stage.
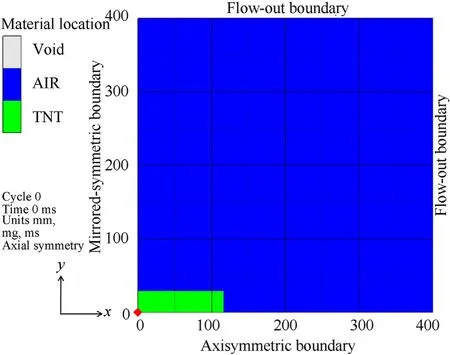
Fig.1.FE model and boundary condition for center-initiated cylindrical charge and air.
The output of first stage with a mesh size of 0.5 mm is remapped into the second stage with different mesh sizes.Fig.5 shows the overpressure-time histories with mesh sizes of 5 mm,10 mm,20 mm and 40 mm at different scaled distances.It is noted that numerical predictions by mesh sizes of 5 mm and 10 mm have no significant difference.With the considerations of both the numerical accuracy and computational cost,a mesh size of 10 mm is used for the second stage.
Considerably recognized empirical formulas for the peak overpressure generated from spherical charge are available,such as the UFC 3-340-2 formula[1],Sadovskyi formula[28],Baker formula[29]and Henrych formula[30].Fig.6 shows the comparison of peak overpressure between numerical predictions and these formulas at scaled distances varied from 0.3 m/kgto 6.0 m/kg.It is observed that the diversity is evident for these formulas,especially in near field.The numerical predictions agree well with those by the UFC 3-340-2 formula and the Henrych formula,and consequently,the numerical model is considered to be sufficiently accurate.
3.Results and discussion
Based on the numerical model,detailed analyses of free air blast loads generated from center-initiated cylindrical charges with various aspect ratios are conducted in this section.
3.1.Pressure contours and material location contours
Pressure contours provide qualitative information of the distribution of shock waves,which can lay a foundation for subsequent quantitative analyses of the influences of aspect ratio and orientation on blast loads.
The pressure contours of cylindrical charges with aspect ratiosof 1,4 and 8 at different time are respectively shown in Figs.7—9.For a clear presentation of the evolution process of shock waves,the pressure contours at different time for a specified aspect ratio are illustrated in a single figure.Unlike the uniformly spherical shock waves generated from spherical charges,the shock waves generated from cylindrical charges do not enter the surrounding air as spherical waves,nor at the same instant over the entire charge surface.It can be observed that shock waves are initially generated in three different regions(Figs.7a-9a).These different shock waves are experimentally observed in Ref.[20]and are usually respectively named as primary end wave,bridge wave and primary side wave[9],as shown in Fig.10.The corresponding three regions can be divided and named as the axial region,the vertex region and the radial region.

Fig.2.Schematic diagram of remapping strategy.
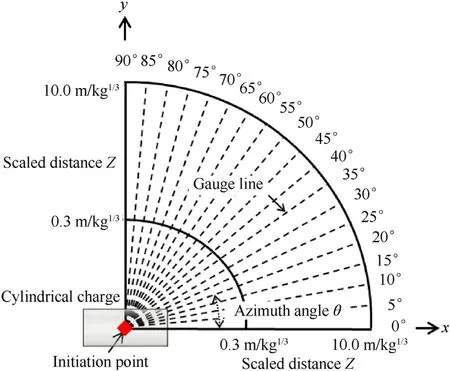
Fig.3.Definitions of azimuth angle and gauge.
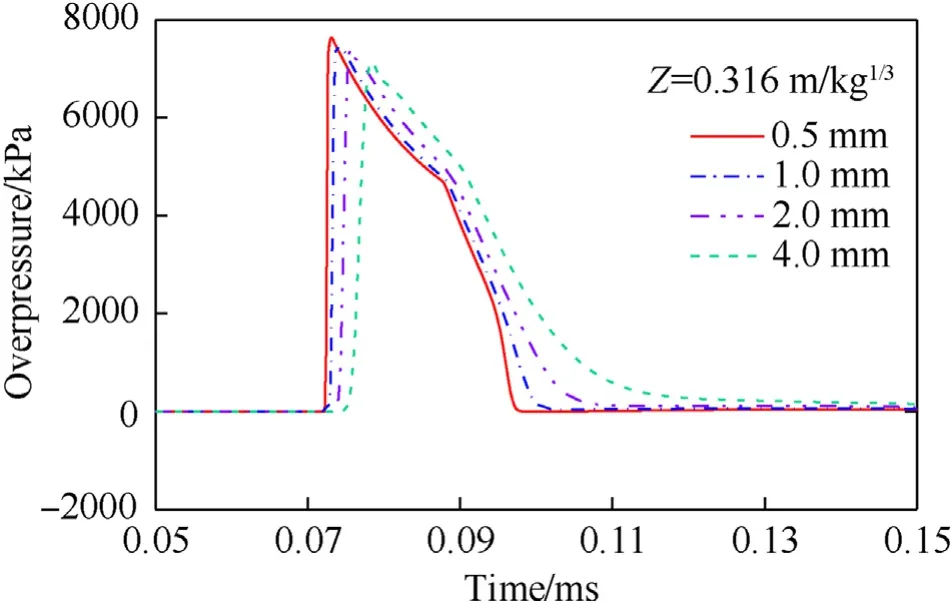
Fig.4.Numerically predicted overpressure-time histories at Z=0.316 m/kg1/3 by various mesh sizes.
As observed from Figs.7a-9a,for a small scaled distance(e.g.,Z≤0.21 m/kg),the strengths of primary end wave,primary side wave and bridge wave are always in a descending order,as more energy is released near the axial direction and near the radial direction at the beginning of explosion.Similar to the regionalization shown in Fig.10,three typical regions for the detonation product can also be divided as the axial region,the vertex region and the radial region(divided by dash lines shown in Fig.11).Previous studies[3,17]demonstrated that the maximum peak overpressure always emerges along the direction of the largest presented area.The presented area in each region defined as the area that can be seen in a given direction is rather different.The strengths of primary end wave,bridge wave and primary side wave in respective three regions are different,which can be clearly observed from the pressure contours shown in Figs.7—9.For example,the strength of primary end wave is larger than the bridge wave but smaller than primary side wave for an aspect ratio of 4 at the time of 0.1301 ms shown in Fig.8b.
From Fig.11,it is observed that the presented area in each region is closely related to the aspect ratio.The presented areas in the radial and vertex regions increase and decrease with the increase of aspect ratio,respectively.It is interesting to note that the presented area in the radial region is far greater than other regions for a largevalue of aspect ratio,e.g.,an aspect ratio of 8 shown in Fig.11.Consequently,the distributions of blast loads will be basically identical for large aspect ratios,which will be further demonstrated in the following sections.
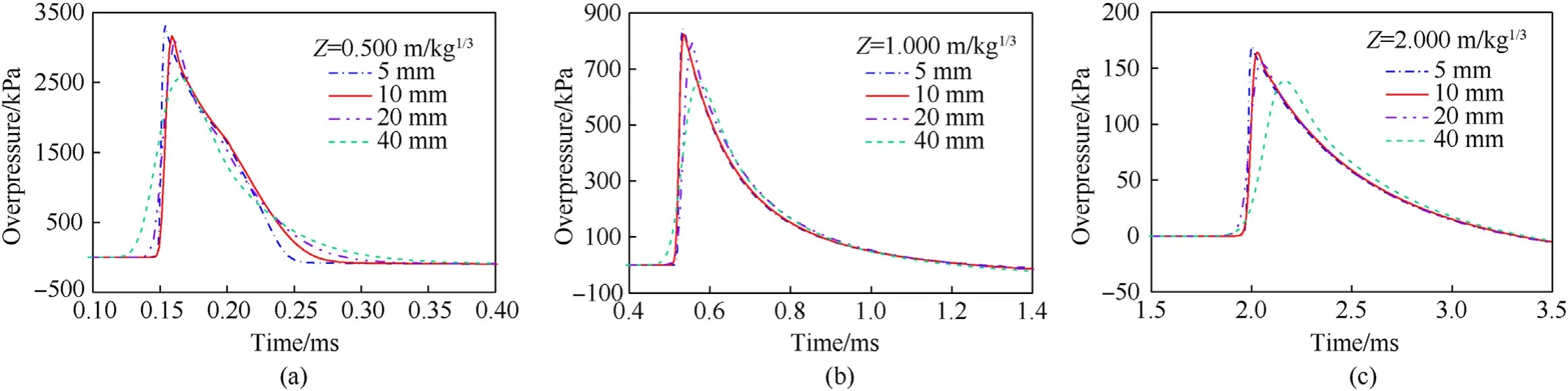
Fig.5.Numerically predicted overpressure-time histories by various mesh sizes at scaled distances of(a)0.500 m/kg1/3,(b)1.000 m/kg1/3 and(c)2.000 m/kg1/3.
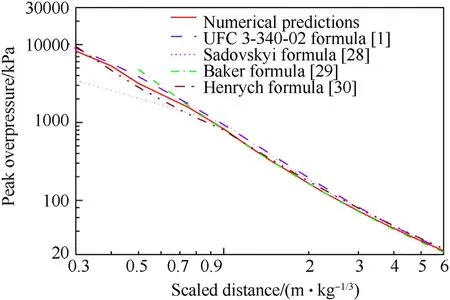
Fig.6.Comparison of peak overpressure between numerical predictions and empirical formulas.
Equipped with the concept of the presented area,the distributions and evolutions of shock waves can be analyzed thoroughly.For the aspect ratio of 1,as shown in Fig.11a,the presented area can be sorted in a descending order,i.e.,the vertex region>the axial region>the radial region.Thus,at 2.554 ms shown in Fig.7b,the pressures in the vertex region are larger than those in the axial and radial regions.Similar to the dash lines shown in Fig.10,part of the bridge wave located on the side of the axial region falls behind the primary end wave,which gradually propagates to the axial direction and leads to the so-called secondary shock(Fig.7b).However,the other part of the bridge wave located on the side of the radial region and the primary side wave nearly advance side by side,so that the secondary shock wave is unclear under this circumstance shown in Fig.7b.As the secondary shock wave continues propagating to the axial direction,the secondary shock waves on both sides of the symmetry axis meet together,leading to an obvious enhancement(Fig.7c).This enhanced shock wave then propagates to the opposite direction and finally results in the so-called tertiary shock(Fig.7d).
For the aspect ratio of 4,at 0.1301 ms shown in Fig.8b,the pressures can be sorted as the radial region>the axial region>the vertex region.The primary end wave and the primary side wave spread to the vertex direction originally(Fig.8b)and then interact with the bridge wave.Consequently,the secondary shock wave in the axial region can be observed in Fig.8c(similar to the analysis of aspect ratio of 1),which gradually catches up with the primary end wave,so that it no longer exists at the time of 11.15 ms shown in Fig.8d.
For the aspect ratio of 8,the pressures in the radial region are far greater than those in the other regions at the time of 0.6156 ms shown in Fig.9b.Therefore,the primary side wave quickly propagates to the vertex region and then the axial region.Eventually at the time of 8.980 ms shown in Fig.9d,the pressures are almost uniformly distributed in all directions,the shock front can be considered as a spherical one.
To validate the analyses above,the pressure and material location contours predicated by numerical models are compared with experimental observations.The distribution of detonation product from the center-initiated cylindrical charge with a very large aspect ratio was pictured by Zuo et al.[31]using the high-speed camera.Fig.12 shows detonation product at the time of 20μs when shock waves propagate into the air initially.The profile of detonation product is in a“rhombus”shape and is similar to that by numerical predicted one in Fig.11d for an aspect ratio of 8.
The development of bridge wave and secondary shock by a PE4 cylindrical charge with an aspect ratio of 4 was experimentally pictured by Knock et al.[20]and is shown in Fig.13,which confirms the analysis regarding the bridge wave and secondary shock above.
3.2.Peak overpressure
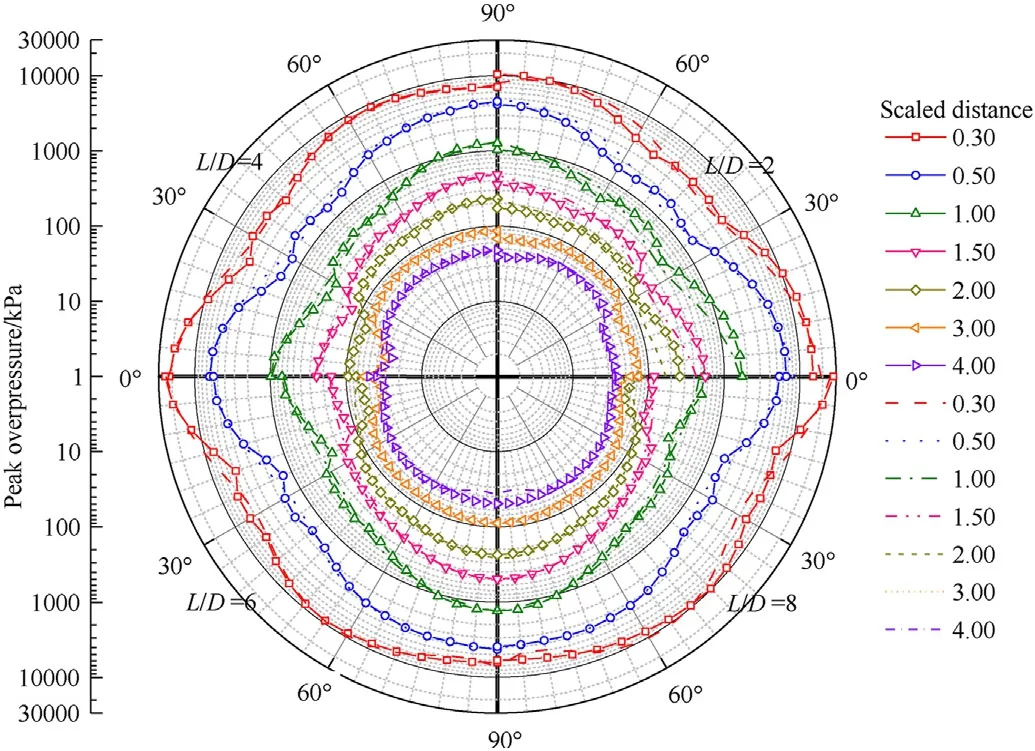
Fig.14 presents the distributions of peak overpressures generated from center-initiated cylindrical charges predicted by numerical simulation in polar coordinates.As the considered azimuth angle varies from 0to 90(due to symmetry,shown in Fig.3),a complete polar coordinate diagram can present the distributions of peak overpressures with four different aspect ratios.
Based on Fig.14,some interesting phenomena can be observed.Firstly,significant differences of the distributions of peak overpressures can be found for different aspect ratios.However,the differences decrease gradually with the increase of aspect ratio,and the distributions are basically identical for large values of aspect ratios of 7 and 8.This can be explained by the fact that the presented area near the radial direction is far greater than other directions for a large value of aspect ratio,as discussed in Section 3.1.Secondly,at small scaled distances(e.g.,Z<1.25 m/kgfor the aspect ratio of 2),the peak overpressure contours expand more significantly along the axial direction than other directions.While with the increase of the scaled distance,the peak overpressure contours gradually evolve into a“multi-leafed rose”shape(e.g.,Z=1.25 m/kg,note that only quarter is shown in Fig.14).This can be expected since three different regions are noted in previous section and the strengths of shock waves in respective three regionsare different.Finally,with further increase of the scaled distance,the“multi-leafed rose”shape heals into an approximate circle,and this evolution process speeds with the increase of the aspect ratio.
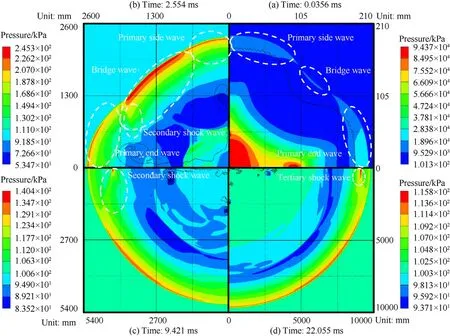
Fig.7.Pressure contours for L/D=1 at time of(a)0.0356 ms,(b)2.554 ms,(c)9.421 ms and(d)22.055 ms.
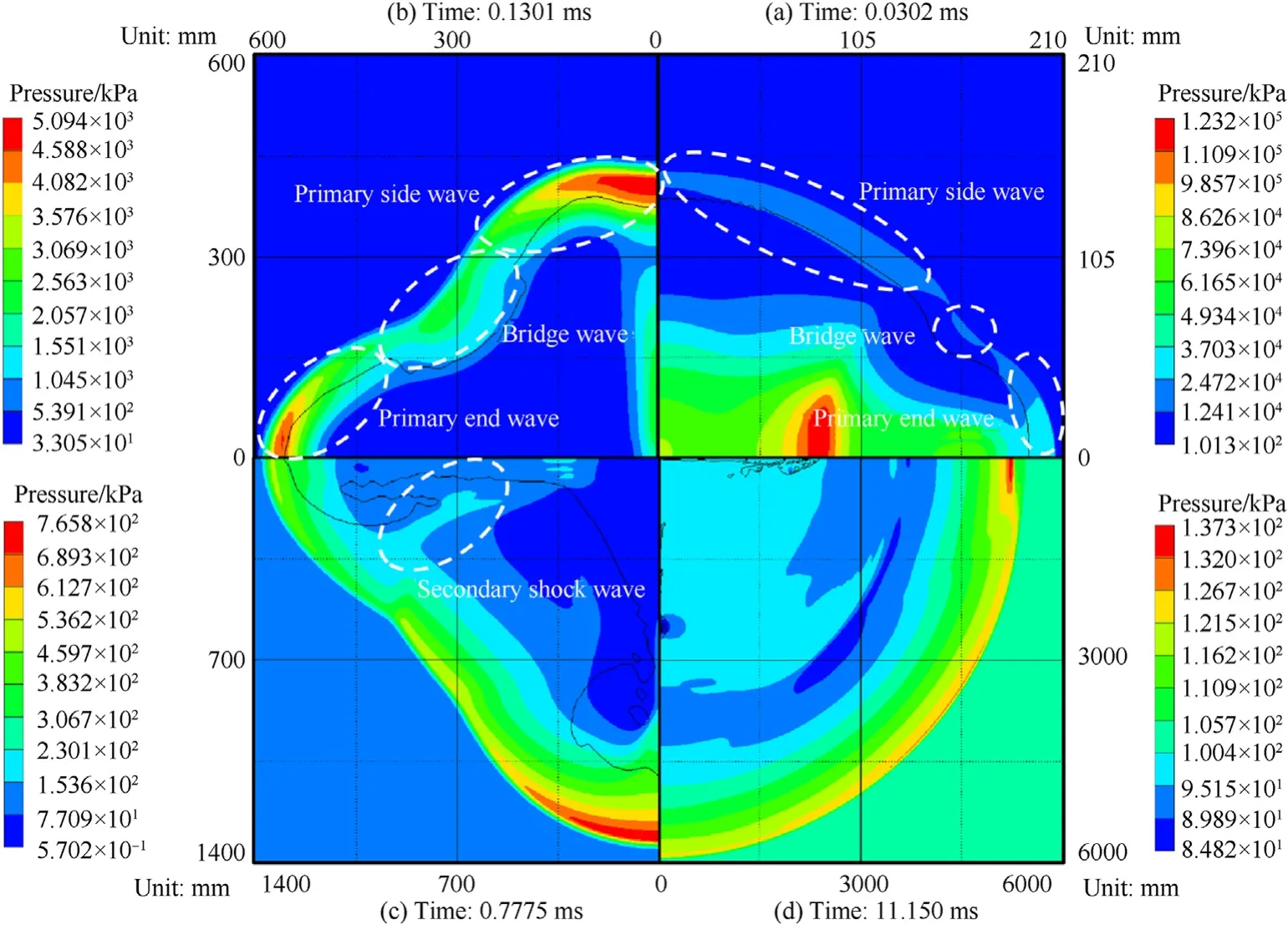
Fig.8.Pressure contours for L/D=4 at time of(a)0.0302 ms,(b)0.1301 ms,(c)0.7775 ms and(d)11.150 ms.
3.2.1.Shape factor for peak overpressure
To correlate the peak overpressures and impulses generated from cylindrical charges with the ones generated from spherical charge with equal mass,the shape factors Sand Sare introducedand defined as,
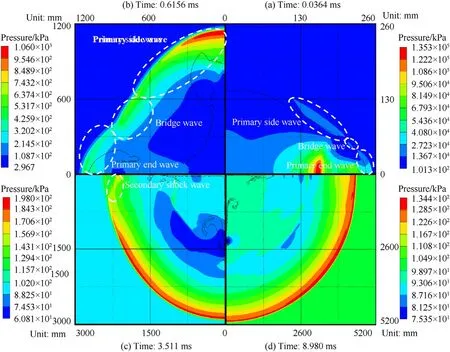
Fig.9.Pressure contours for L/D=8 at time of(a)0.0364 ms,(b)0.6156 ms,(c)3.511 ms and(d)8.980 ms.
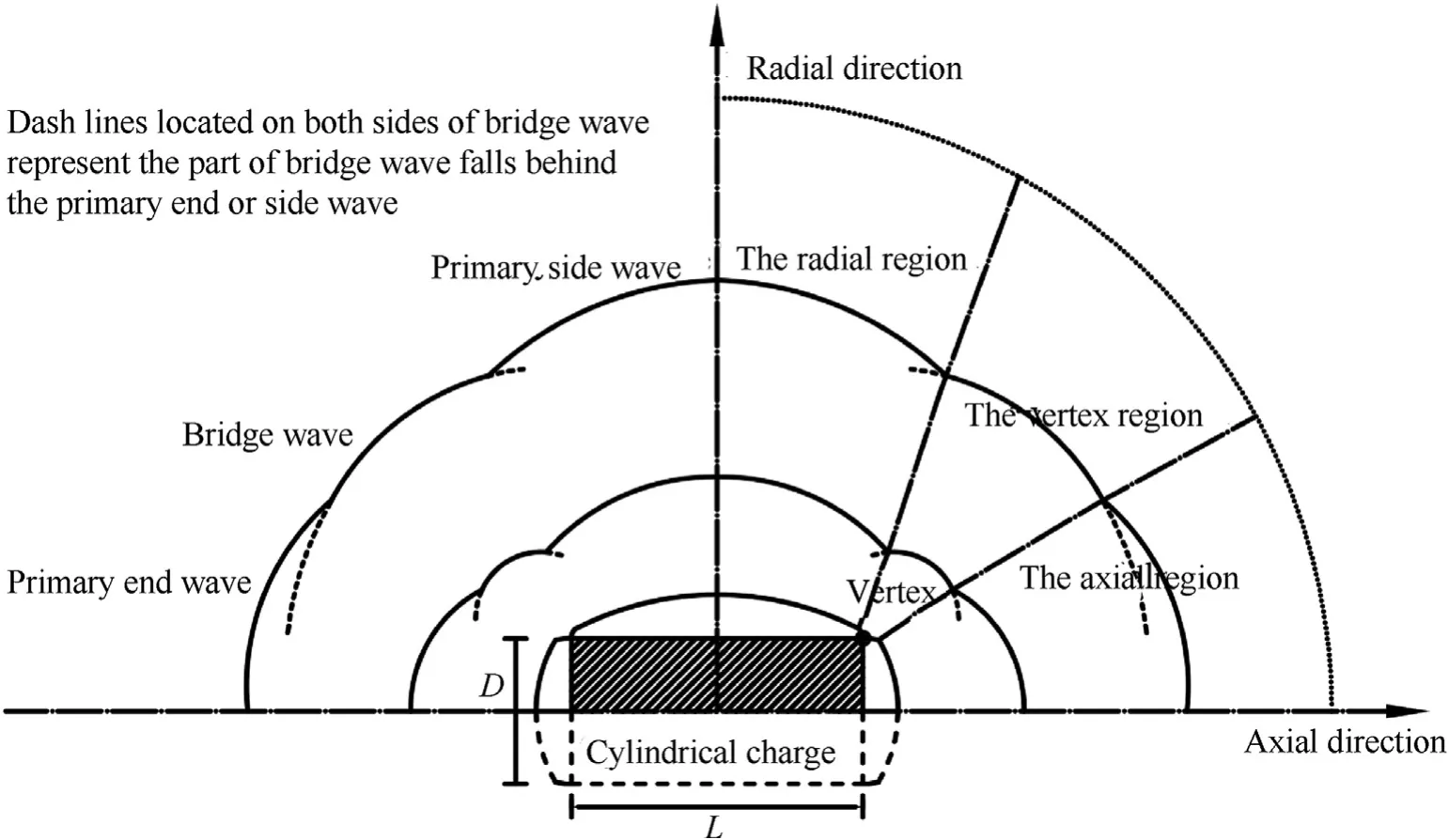
Fig.10.Development of shock waves[9]and regionalization.

where p and i are the peak overpressure and impulse,and the subscripts cyl and sph denote the quantities generated from the cylindrical and spherical charges,respectively.
To conveniently investigate the tendency of shape factor Swith the aspect ratio and scaled distance,it is shown in a rectangular coordinate in Fig.15.Note that the three regions,i.e.,the axial region,the vertex region and the radial region,are qualitatively defined previously in Section 3.1,and the distributions of peak overpressures in three regions are rather different.Consequently,the characteristics of Sin each region are totally different,which are marked in red lines,green lines and blue lines,respectively.However,the quantitative range of each region varies with the aspect ratio.For example,the range of the radial region is changed from[80,90]for L/D=1 to[65,90]for L/D=8.
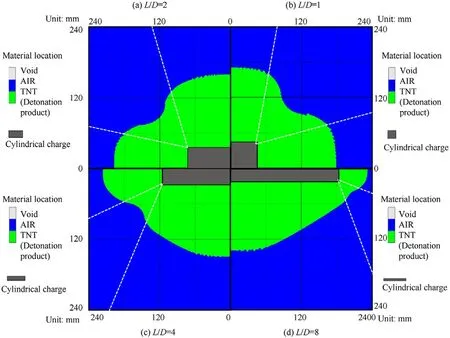
Fig.11.Material location contours when shock waves initially separate from the detonation product for(a)L/D=1,(b)L/D=2,(c)L/D=4 and(d)L/D=8.

Fig.12.Distribution of detonation product from the center-initiated cylindrical charge at 20 μs[31].
To clearly show the primary shock and secondary shock,the shape factor Sdetermined by the larger value of peak overpressures between the primary shock and secondary shock is shown in solid lines,while the dash lines are used to illustrate Sdetermined by primary shock when its peak overpressure is smaller than secondary shock.As shown in Fig.15,the Sin the axial region(red lines)is the highest among three regions at a small scaled distance.It decreases as the lowest one with the increase of scaled distance,and then increases to the highest rapidly with help of the secondary shock(note that dash lines illustrate the Sdetermined by the primary shock when its peak overpressure is smaller than the secondary shock).Finally,it slowly decreases and approaches to 1.0.In the vertex region(green lines),the Sdecreases to the lowest rapidly at a small scaled distance,then increases to a value slightly greater than 1.0 and remains almost stable with the increase of scaled distance.The Sin the radial region(blue lines)increases within small scaled distance,then decreases to a value slightly less than 1.0 with the increase of scaled distance,and finally approaches to 1.0.It is also interesting to note that the Sgradually tends to be consistent with the increase of aspect ratio,as expected,since the presented area in the radial region is far greater than other regions for a large value of aspect ratio,as discussed previously.
3.2.2.The maximum peak overpressure
The maximum shape factor S(S)defined as the maximum value among the shape factor S(S)is very important for the blast-resistant design.Generally,the Sis dependent on the aspect ratio and scaled distance and can be determined using the data shown in Fig.15.
The relationships of the Sand the scaled distance for various aspect ratios are shown in Fig.16.Based on the orientation where the Semerges observed in Fig.15,the Scan be divided into three different stages.For the first stage involved with relatively small scaled distance,the Semerges along the axial direction,which can be easily observed in Fig.15 and marked by red lines in Fig.16.For the second stage involved with medium scaled distance(marked by green lines in Fig.16),the orientations where Semerges are inconsistent for different aspect ratios,i.e.,it emerges along the vertex direction for L/D=1,along the radial direction and vertex direction for L/D=2 and along the radial direction for L/D≥3,as observed in Fig.15.For the third stage involved with a large scaled distance(marked by blue lines in Fig.16),the Semerges along the axial direction again and can be clearly observed in Fig.15.
Based on the discussion above,it is found that the Salways emerges along the axial or radial direction for L/D≥3.However,this is not true for a small aspect ratio(at least L/D≤2 concerned in the present study)in the second stage,which deserves further discussion.Specifically,for L/D=1,the emerges in the vertex region and gradually shifts from 25to 45with the increase of scaled distance from 2.68 m/kgto 5.00 m/kg(Fig.15a).While for L/D=2,the emerges in the vertex region and gradually shifts from 65to 45with the increase of scaled distance from 3.00 m/kgto 3.85 m/kg(Fig.15b).Since this range of scaled distance is small and the values of in the vertex region and radial region are comparable,it can be approximately considered that the emerges along the radial direction for L/D=2 in the second stage.Combined with the analyses in Section 3.1,the vertex region where the emerges is in accordance with the region where the bridge wave is stronger than the primary end wave and primary side wave.In other words,the bridge wave causes the fact that the does not always emerge along the axial or radial direction for a small aspect ratio.
The scaled distances between the three stages,defined as and respectively,is useful for further study on empirical determination of blast loads in Section 4.Based on the data shown in Fig.16,and are curve-fitted as,

The correlation coefficient is r=0.9958 for Zand r=0.9996 for Z.As shown in Fig.17,the fitted curves of Zand Zdivide the area enclosed by aspect ratio and scaled distance into three different regions.For the two regions with red background,the Semerges along the axial direction.In the remaining regions,the Semerges along the radial direction for L/D≥2(green background),while it does not always emerge along the axial or radial direction for L/D<2(blue background),as discussed above.The equations of Zand Zare effective to predict the orientation where the maximum peak overpressure emerges by using the aspect ratio as the only variable.

Fig.13.Development of bridge wave and secondary shock from cylindrical PE4 charge with L/D=4 at the time of(a)1 ms and(b)3.6 ms[20].
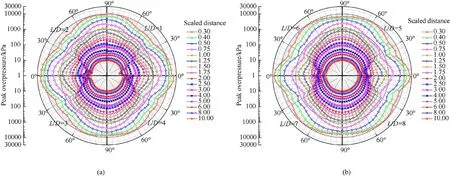
Fig.14.Distribution of peak overpressures in polar coordinates generated from cylindrical charges for(a)L/D=1,2,3,4 and(b)L/D=5,6,7,8.
3.2.3.Critical scaled distance
Based on previous discussion,it is confirmed that a critical scaled distance exists beyond which the shock waves generated from a cylindrical charge can be approximately considered as spherical waves so that the blast loads can be determined by those generated from a spherical charge with equal mass.This critical scaled distance is very useful for blast-resistant design,which was determined by Sherkar et al.[12]on the assumption that the maximum shape factor Sin the axial and radial directions is less than a critical value of 1.1.However,this assumption has its limitations.Firstly,the maximum shape factor Sdoes not always emerges in the axial or radial direction,especially for a small value of aspect ratio,as discussed in Section 3.2.2.Furthermore,only the Sis considered,but the minimum shape factor S(the minimum value of S)is neglected.
To resolve these issues,the critical scaled distance should be determined on the criterion that the Sis less than 1.1 and the Sis greater than 0.9 in all orientations of a cylindrical charge.As mentioned previously,with the increase of scaled distance,the Sincreases(decreases)to a value slightly greater(less)than 1.0 and remain approximately stable in the vertex(radial)region.However,in the axial region,the Sincreases to a value greater than 1.1 at a relatively large scaled distance and decreases slowly with the increase of scaled distance due to the secondary shock,which can be clearly observed in Fig.15(red lines).Therefore,the proposed criterion can be easily satisfied in the vertex and radial regions,but cannot satisfied in the axial region even at a very large scaled distance greater than 10 m/kg.Note that the Sdetermined by the secondary shock corresponding to the third stage shown in Fig.16 is not too much greater than 1.1(varies from 1.14 to 1.37 for the cases numerically predicted here),and it always emerges at relatively large scaled distance(>3.8 m/kg,can be observed in Fig.16).Thus,an upper limit value of 1.1 is assumed for the Sdetermined by the secondary shock,which would have little influence on blast-resistant design.

Fig.15.Shape factor Sp versus scaled distance at different azimuth angles for center-initiated cylindrical charges with aspect ratios of(a)1,(b)2,(c)3,(d)4,(e)5,(f)6,(g)7 and(h)8.
Based on the criterion and assumption above,the critical scaled distance Zas a function of aspect ratio can be established by curvefitting the corresponding data shown in Fig.15 as,
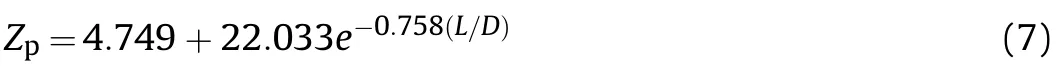
Comparison of the critical scaled distance predicted by Eq.(7)and numerical data is shown in Fig.18.The correlation coefficient is r=0.9969 and a good agreement is observed.Eq.(7)is effective to predict the critical scaled distance beyond which the charge shape effect could be neglected for peak overpressure by using the aspect ratio as the only variable.
3.3.Impulse
Based on the overpressure-time history,the impulse generated from cylindrical charges can be analyzed,which is determined by,

where tis the arrival time of shock front,tis the duration of positive overpressure,Δp(t)is the change of overpressure during a time step d.
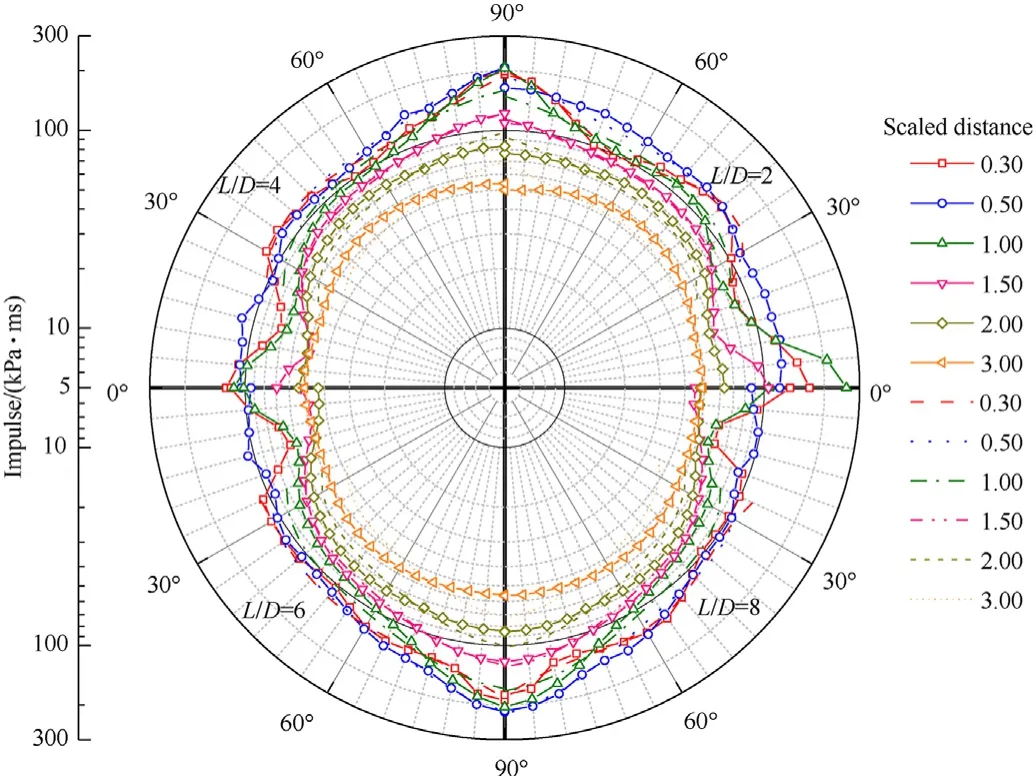
Similar to the peak overpressures,the impulses generated from cylindrical charges predicted by numerical simulation are shown in polar coordinates in Fig.19.It is observed that the distribution of impulses significantly varies as the aspect ratio,and the difference of distributions decreases gradually with the increase of aspect ratio.For large values of aspect ratio,e.g.,L/D=7 and 8,the distributions of impulses tend to be basically identical.The maximum impulses occur at 1.00 m/kgin the axial direction for L/D=1 and 2,0.75 m/kgin the axial direction for L/D=3,4,5 and 6,0.75 m/kgin the radial direction for L/D=7 and 8.
At a small scaled distance(Z<1.25 m/kg),the impulse does not always decrease with the increase of scaled distance.At a relatively large scaled distance(1.25 m/kg≤Z<3.00 m/kg),the impulse in a certain direction decreases with the increase of scaled distance,but significant difference still exists in different directions,as expected.As the scaled distance continues increasing(Z≥3.00 m/kg),the impulses in different directions are nearly identical,and the impulse contour can be approximately regarded as a circular shape.
3.3.1.Shape factor for impulse
The shape factor for impulse Sis shown in Fig.20 as functions of scaled distance and azimuth angle.Similar to the shape factor for peak overpressure Sdiscussed in Section 3.2.1,three regions,i.e.,the axial region(marked by red lines),the vertex region(marked by green lines)and the radial region(marked by blue lines)are divided.In general,the tendency of Sis more complex than that of Sfor the scaled distance less than 3.00 m/kg,then they become nearly identical with the increase of scaled distance.
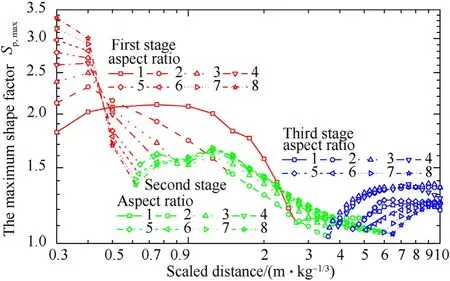
Fig.16.Relationships of Sp,max and scaled distance for various aspect ratios.
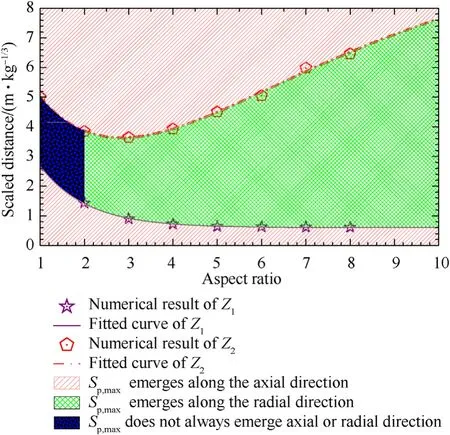
Fig.17.Relationship of orientation of Sp,max between aspect ratio and scaled distance.
At the scaled distance varied from 0.75 m/kgto 3.00 m/kg(for L/D=1,from 0.75 m/kgto 5.00 m/kg),the impulse distribution in the axial region is significantly complex than the other two regions.A steep N-shape tendency is observed,i.e.,the Sincreases rapidly,then decreases sharply,and finally increases again with the increase of scaled distance.At the scaled distance larger than 3.0 m/kg(for L/D=1,larger than 5.0 m/kg),the Sin all three regions gradually approaches to 1.0 and then remains relatively stable.
Similar to the critical scaled distance for overpressure discussed in Section 3.2.3,the critical scaled distance Zbeyond which the charge shape effect could be neglected for impulse can be determined based on the criterion that the Sis less than 1.1 and the Sis greater than 0.9 in all directions surrounding a cylindrical charge.A close observation of Fig.20 demonstrates Zis 4.75 m/kg3 for L/D=1,and is approximate as 3.0 m/kgfor L/D≥2.This indicates that the Zis independent on the aspect ratio when L/D≥2,and the charge shape effect on impulse is significantlysmaller when compared with peak overpressure.Therefore,the critical scaled distance Zgiven in Eq.(7)can be used for the neglect of charge shape effect on blast loads.
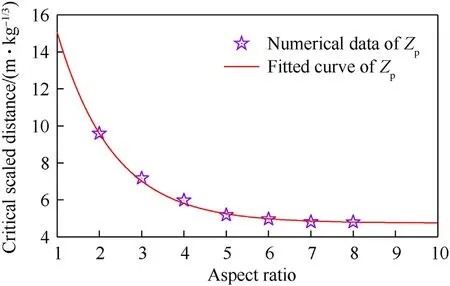
Fig.18.Relationship between critical scaled distance Zp and aspect ratio.
3.3.2.The maximum impulse
The S-scaled distance curves for various aspect ratios are shown in Fig.21.Similar to the Sdiscussed in Section 3.2.2,based on the orientation where the Semerges observed in Fig.20,it can also be divided into different stages.For L/D=1,the Scurve can be divided into six stages where the maximum impulse repeatedly emerges along three directions,i.e.,along the axial direction(red lines),along the vertex direction(green lines)and along the radial direction(blue lines),respectively.For L/D=2,3,4,5 and 6,the Scurves are divided into five stages,and the maximum impulses also repeatedly emerge along the three directions.For L/D=7 and 8,the Scurves are almost coincided with each other,and the maximum impulses sequentially emerge along the radial direction and the axial direction.
In Section 3.2.2,the orientation where the maximum peak overpressure emerges is determined by proposing empirical formulas for two scaled distances Zand Zconnect the three stages.However,it is rather difficult to develop corresponding formulas for impulse,as the orientation where the Semerges is too complicated.
3.3.3.Further discussion
To give some insights into the complicated distribution of impulse,further discussion is made in this section.The important features of the shock wave are an initial discontinuous rise in pressure(shock front)and a followed continuous pressure drop.The pressure drop is caused by a rarefaction wave,which moves faster than the shock wave and leads to an attenuation of shock strength with distance[22].If the rarefaction wave is strong,the pressure will decay rapidly with time after passage of the shock front,and the impulse will be small.Conversely,a weak rarefaction wave will lead to a slow decay of shock pressure with distance and a higher impulse.Thus,the impulse is directly proportional to peak overpressure,but inversely proportional to its rate of decay with distance from the charge.Current guidelines for impulse calculation have two fundamental assumptions.Firstly,it is assumed that there is only one shock front,or at least that there are no other shock fronts between the primary shock and the point at which the pressure first decays back to the ambient value.The second assumption is that the pressure behind the primary shock decays exponentially with time when the shock is very strong,and gradually approaches a linear decay rate as shock strength decreases.
However,the secondary shock generated by cylindrical charges make the impulse calculation relatively complex,especially in the axial region(θ≤25)where secondary shock dominates,as can be observed in Figs.15 and 20.Fig.22 shows the overpressure-time histories for spherical charge and cylindrical charge with L/D=4 in the given azimuth angles at different scaled distances.It is noted previously that the impulse distribution in the axial region at a scaled distance less than 3.00 m/kgis significantly complex than the other two regions,and a steep N-shape tendency between the Sand scaled distance is observed(Fig.20).Therefore,more attention is drawn to this region.
At a small scaled distance Z=0.50 m/kg,the peak overpressures generated from cylindrical charge at different azimuth angles are compared with that from spherical charge,which can be sorted in descending order as 0(axial direction)>90(radial direction)>spherical charge>45,as shown in Fig.22a.However,the strong shock wave is always followed by a strong rarefaction wave and vice versa,thus this descending order is not hold for impulse,as can be observed in Fig.20d.At Z=0.75 m/kg(Fig.22b),both the peak overpressures and positive phase durations at directions of 0and 5are larger than the spherical ones,which leads the Sfar greater than 1.0 observed in Fig.20d.At Z=1.00 m/kg(Fig.22c),the positive phase duration is shorter than the spherical one.Therefore,the Sis less than 1.0(Fig.20d)although the Sis larger than 1.0(Fig.15d).At a large scaled distance Z=3.00 m/kg(Fig.22d),the secondary shock front emerges between the primary shock front and the point at which the pressure decays back to theambient value,and the peak overpressure of the secondary shock is larger than that of the primary shock.This leads to the significant extension of positive phase duration,and thus the Sgradually increases to a value slightly larger than 1.0 observed in Fig.20d.In summary,the complex N-shape tendency between the Sand scaled distance in the axial region shown in Fig.20 is mainly caused by the secondary shock.
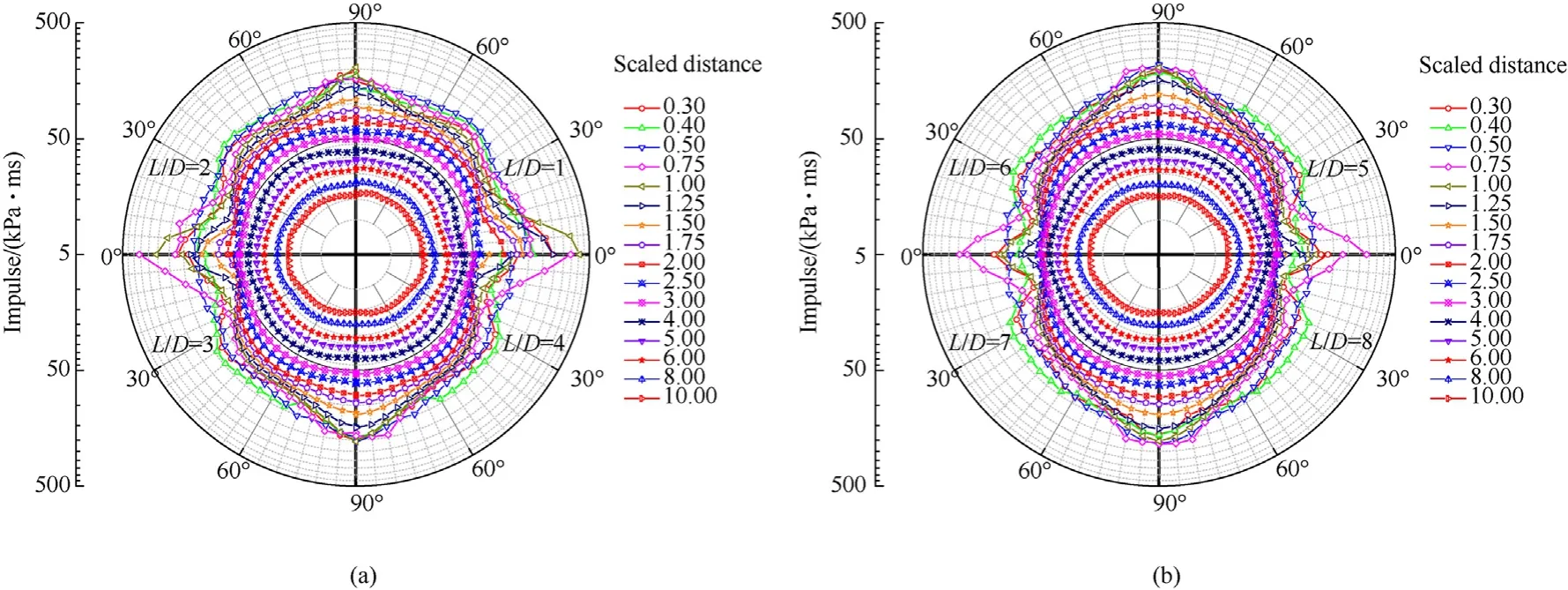
Fig.19.Distribution of impulses in polar coordinates generated from cylindrical charges for(a)L/D=1,2,3,4 and(b)L/D=5,6,7,8.
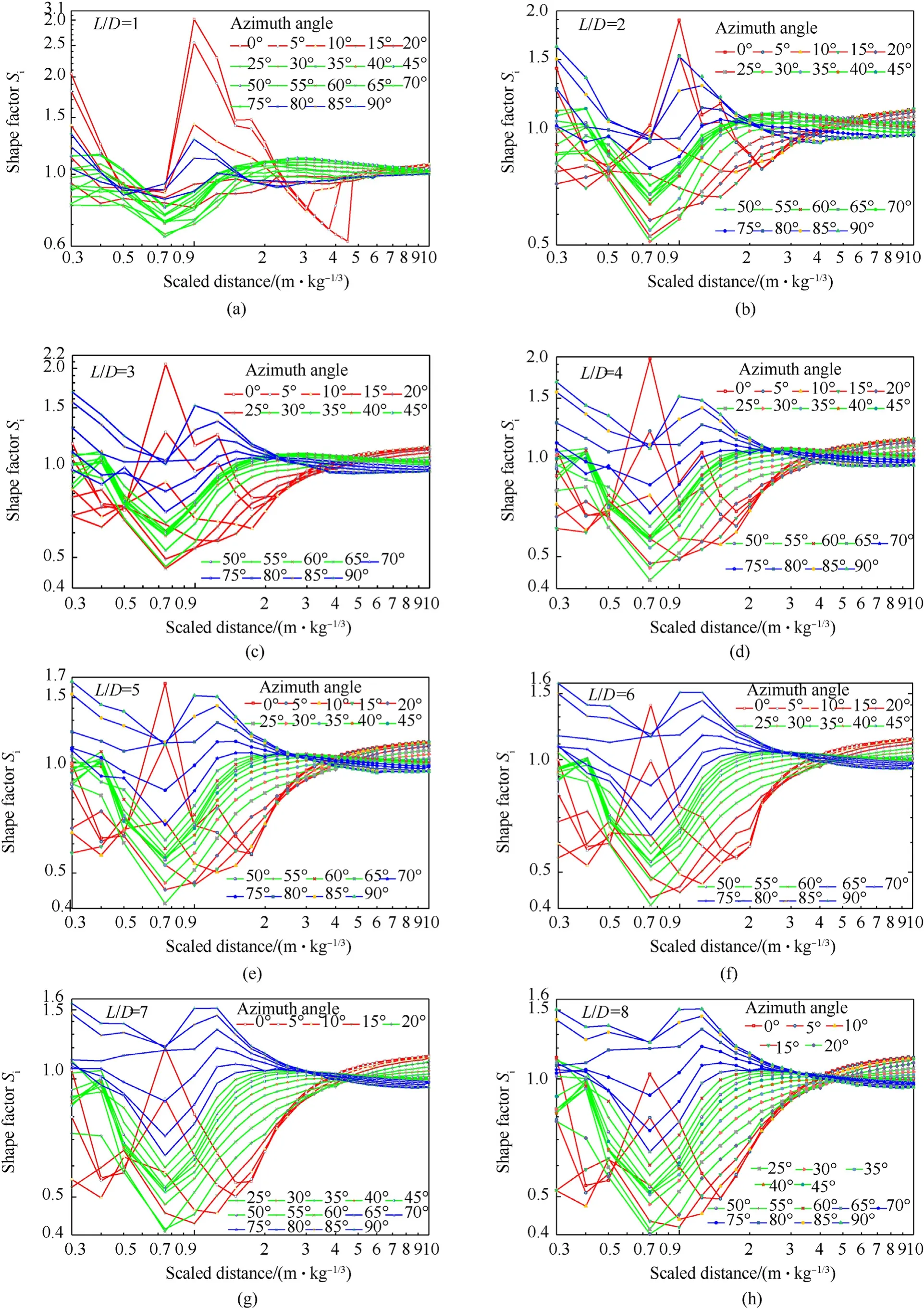
Fig.20.Shape factor Si versus scaled distance at different azimuth angles with aspect ratios of(a)1,(b)2,(c)3,(d)4,(e)5,(f)6,(g)7 and(h)8.
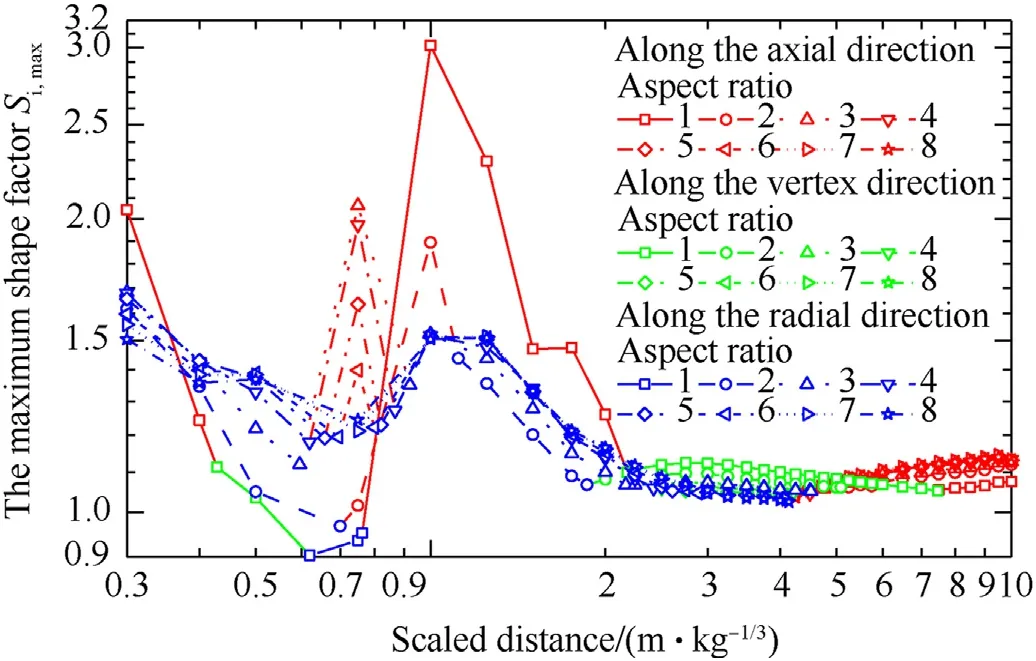
Fig.21.Relationships of Si,max and scaled distance for various aspect ratios.
4.Empirical formulas for free air blast loads
Based on the analyses in Section 3,the free air blast loads(overpressure and impulse)generated from center-initiated cylindrical charges depend on the scaled distance Z,the aspect ratio L/D and the azimuth angle θ.Using the numerical data herein,an attempt is made in this section to develop the empirical formulas for blast loads that are convenient for engineering use.
4.1.Empirical formula for peak overpressure
To construct the empirical formula for peak overpressure,some important aspects on its distribution should be considered.
Firstly,the distributions in the three regions are different,which leads to the“multi-leafed rose”curve in a polar coordinate(Fig.14).This can be captured by a trigonometric function as a·sin(jθ),where the constant a determines the size of the“leaf”,θ is the azimuth angle and j is a constant governs the maximum number of leaves.The maximum number of leaves should be eight as three regions are divided in one quadrant(Fig.14),so that the maximum value of j is four.
Secondly,the orientation where the maximum peak overpressure emerges in the three stages are different(Fig.16).This can be considered by a piecewise function divided by two scaled distances Zand Z.Furthermore,the critical scaled distance Zshould be considered,beyond which the charge shape effect could be neglected and the blast loads can be determined by those generated from a spherical charge with equal mass.Consequently,on the one hand,the scaled distance should be divided as three ranges,i.e.,0.3 m/kg≤Z≤Z,Z
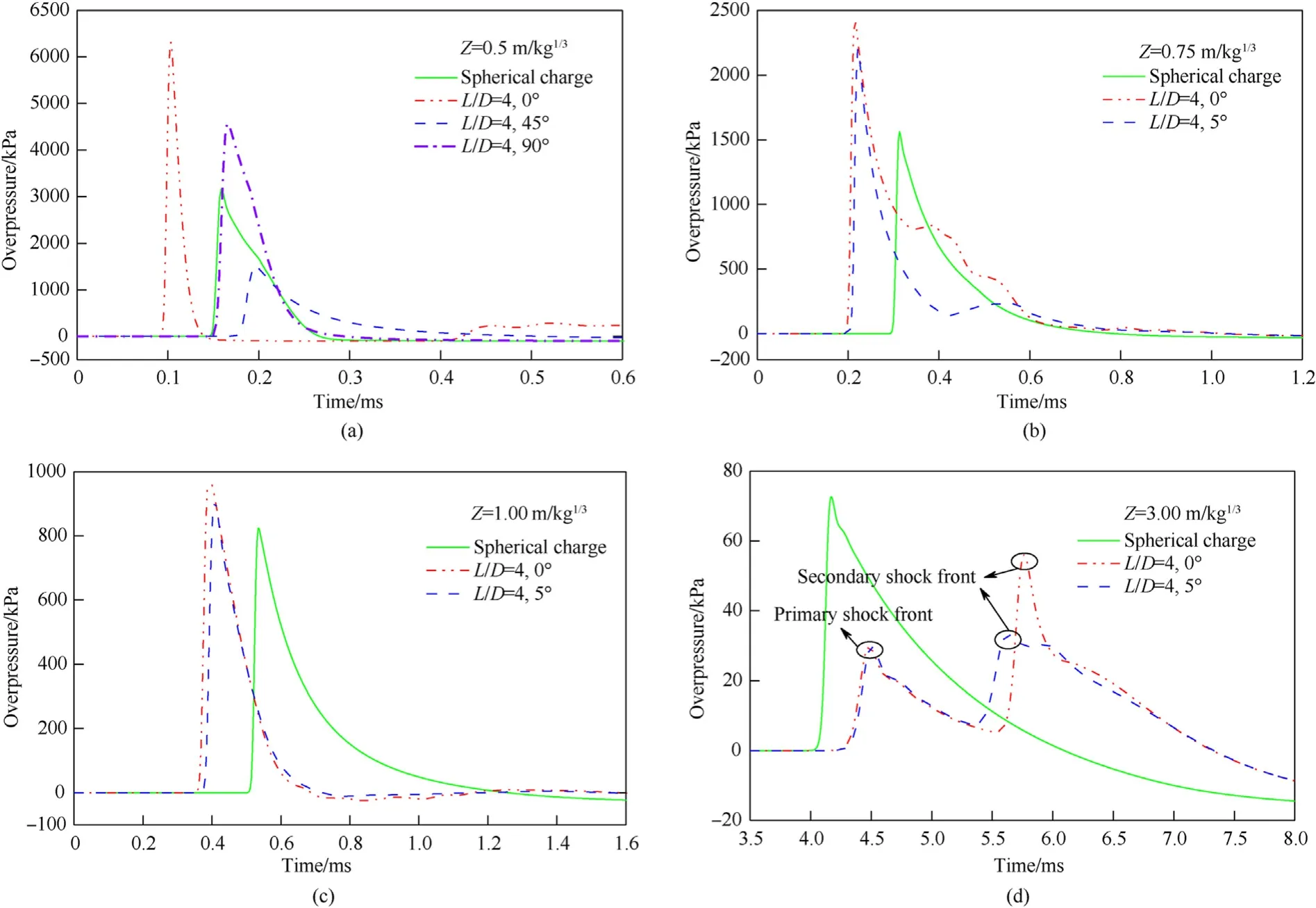
Fig.22.Overpressure-time histories for spherical charge and cylindrical charge with L/D=4 in the given azimuth angles at scaled distances of(a)0.50 m/kg1/3,(b)0.75 m/kg1/3,(c)1.00 m/kg1/3 and(d)3.00 m/kg1/3.
Thirdly,the distribution of peak overpressure gradually tends to be consistent with the increase of aspect ratio.Thus,a logarithmic function can be used to quantify the effect of aspect ratio on peak overpressure.Furthermore,the L/D<2 data should be excluded as the distribution pattern is significantly different from that of L/D≥2,especially at the second stage shown in Figs.15 and 16.
With a thorough consideration of the aspects above,the empirical formula to predict the peak overpressure generated from cylindrical charges is developed as,
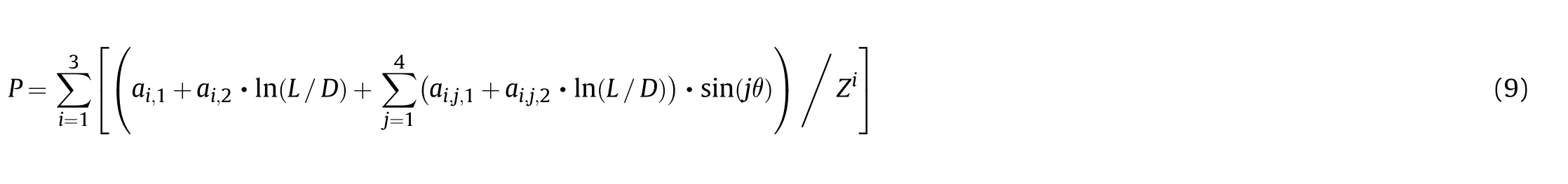
where L/D is the aspect ratio,θ is the azimuth angle ranging from 0to 90,Z is the scaled distance given as R/Mwith R and M being the standoff distance and charge mass,respectively,and i and j are positive integers.a,a,aand aare constants determined by curve-fitting the numerical data for the three ranges of the
scaled distance respectively as discussed above,which are presented in Table 2.The correlation coefficients are r=0.9724 for 0.3 m/kg≤Z≤Z,r=0.9908 for Z Table 2Constants in Eq.(9)by curve-fitting peak overpressure data. Fig.23 shows the comparison of predicted peak overpressures by Eq.(9)with numerical data,and in general an excellent agreement is observed.Therefore,Eq.(9)can be used to predict peak overpressure generated from center-initiated cylindrical charges in arbitrary orientation with the conditions that L/D≥2 and 0.3 m/kg≤Z≤Z.For Z>Z,the classical formula for spherical charge with equal mass can be used. The distribution of impulses is also divided into three regions.In the axial region(θ≤25),the complex N-shape tendency is observed,which is mainly caused by the secondary shock discussed in Section 3.3.3.The complex N-shape tendency makes the development of an accurate empirical formula of the impulse in the axial region infeasible,so the impulse in other two regions(25≤θ≤90)is mainly concerned in this section. A close examination of the distributions of peak overpressure and impulse shown in Figs.14 and 19 indicates that they have some similarities in shape.Furthermore,the fundamental patterns are generally similar,e.g.,the“multi-leafed rose”shape and the gradual consistent tendency of impulse distribution with the increase of aspect ratio.Consequently,Eq.(9)is slightly modified for prediction of impulse generated from cylindrical charges with L/D≥2 as, where the azimuth angle θ is ranged from 25to 90.Particularly,Zis a scaled factor different from the scaled distance Z in Eq.(9),which is defined as R/M.The value of superscript is determined as 2/3 instead of 1/3 as previous study by Knock et al.[20,21]demonstrated that it can well predict the impulse in the radial and axial directions.a,a,aand aare constants,which are determined by curve-fitting the numerical impulse data and are presented in Table 3.The correlation coefficient is r=0.9106. Table 3Constants in Eq.(10)by curve-fitting impulse data. Comparison of the predicted impulses by Eq.(10)withnumerical data is shown in Fig.24,and a good agreement can be observed.Thus,Eq.(10)can be used to predict impulse generated from center-initiated cylindrical charges with the conditions that L/D≥2,0.3 m/kg≤Z≤3 m/kgand 25≤θ≤90.For a scaled distance larger than 3 m/kg,the impulse predicted by the spherical charge with equal mass can be used,as the charge shape effect could be neglected for impulse. Fig.23.Comparison of predicted peak overpressures by Eq.(9)(dash curves)and numerical data(solid curves). Fig.24.Comparison of predicted impulses by Eq.(10)(dash curves)and numerical data(solid curves). This paper presents a numerical investigation on the free air blast loads generated from center-initiated cylindrical charges.It involves identifying the influences of aspect ratio and orientation on the blast loads based on a detailed analysis of numerical results,and then establishing empirical formulas for peak overpressure and impulse.Several conclusive remarks are given as follows: (1)The aspect ratio of cylindrical charges significantly affects the distribution of blast loads,while this effect decreases gradually with increase of aspect ratio,and distributions are basically identical for large values of aspect ratios.Based on the different distribution patterns of blast loads,three regions,i.e.,the axial region,the vertex region and the radial region are identified. (2)The propagation of bridge wave causes the maximum peak overpressure does not always emerge along the axial or radial direction for a small aspect ratio,and its interaction with primary waves leads to the secondary shock.The secondary shock further causes the complexity of impulse distribution.These facts make the blast loads generated from cylindrical charges significantly complex than those by spherical charges. (3)The empirical formula for the orientation where maximum peak overpressure emerges is given as a function of aspect ratio,but corresponding formula for maximum impulse cannot be obtained due to its complexity.For peak overpressure,the critical scaled distance beyond which the charge shape effect could be neglected is also curve-fitted using the aspect ratio as the only variable.For impulse,the critical scaled distance is independent on the aspect ratio and is a constant value 3.0 m/kgfor aspect ratio no less than 2.The charge shape effect on impulse is significantly smaller when compared with peak overpressure. (4)The empirical formula is developed to predict the free air blast loads generated from center-initiated cylindrical charges with varied aspect ratio in arbitrary orientation,in which the aspect ratio should be no less than 2 and the valid scaled distance ranges from 0.3 m/kgto the critical scaled distance.For peak overpressure,all orientations around the charges are considered,but for impulse,azimuth angles between 0and 25are excluded due to its complex N-shape tendency in this region. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. This study was supported by the National Natural Science Foundations of China(51808550,52078133)and the China Postdoctoral Science Foundation(2020M671296).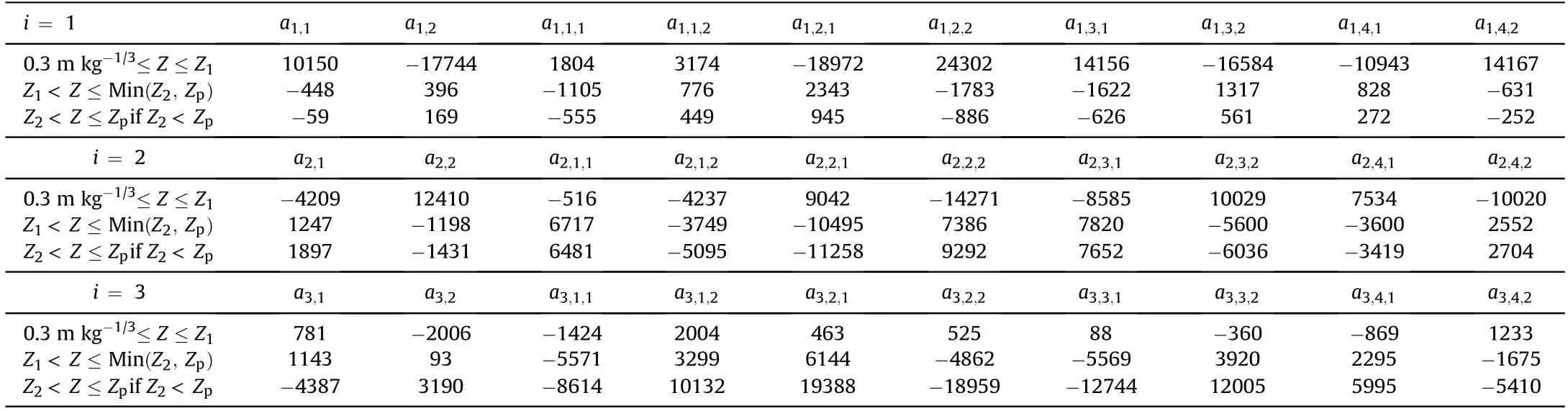
4.2.Empirical formula for impulse
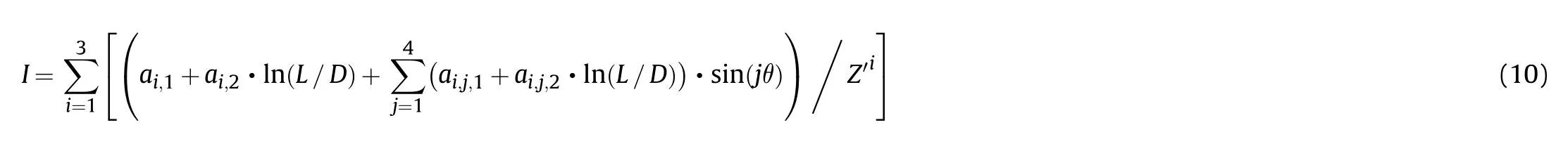
5.Conclusion
杂志排行
Defence Technology的其它文章
- 3D laser scanning strategy based on cascaded deep neural network
- Damage analysis of POZD coated square reinforced concrete slab under contact blast
- Autonomous maneuver decision-making for a UCAV in short-range aerial combat based on an MS-DDQN algorithm
- The properties of Sn—Zn—Al—La fusible alloy for mitigation devices of solid propellant rocket motors
- The surface activation of boron to improve ignition and combustion characteristic
- Natural convection effects on TNT solidification inside a shaped charge mold
