Vulnerability assessment to projectiles:Approach definition and application to helicopter platforms
2022-09-22LomazziCadiniGiglioManes
L.Lomazzi,F.Cadini,M.Giglio,A.Manes
Politecnico di Milano,Department of Mechanical Engineering,Milan,I-20156,Italy
Keywords:Vulnerability Survivability Helicopter Projectile Threat
ABSTRACT Survivability is defined as the capability of a platform to avoid or withstand a man-made hostile environment.Military aircraft in particular,but also other kinds of platforms subjected to external,impacting threats,are commonly designed according to increasing survivability requirements.The concept of survivability was first formalized by R.Ball in 1985 in its seminal work on combat aircraft survivability.On the basis of the theory presented in his work,many computer programs have been developed which implement the modelling techniques and computations required by vulnerability assessments.However,a clear and general view of the operative computational procedures is still lacking.Moreover,to date only a limited number of applications to helicopter platforms have been investigated in the survivability field,even though these platforms experience numerous flight conditions exposing the system to different types of threats.In this context,this work aims at establishing a multi-purpose general framework for the vulnerability assessment of different types of platforms subjected to external threats,with a focus on helicopters.The in-house software specifically developed for this application is here described in detail and employed to present a case study on a representative military helicopter.
1.Introduction
Aircraft survivability is defined as the capability of a platform to avoid or withstand a man-made hostile environment,while killability,or kill probability,identifies the probability that the encounter with a threat results in the kill of the platform[1].These concepts originated in the aeronautical field in the early days of the 20th century,during World War I[1].In that period,two main actions were performed by pilots to enhance survivability,i.e.,(i)flying above the maximum altitude of the enemy weapons and(ii)sitting on stove lids,which would stop eventual incipient threats.The first action pertains to what is commonly called susceptibility,which is defined as the inability of an aircraft to avoid the elements of an enemy's defense that make up the man-made hostile environment[1].The second action concerns the stove lids that were employed to stop projectiles which would have hit the pilots,thus reducing the vulnerability of the platform,i.e.,improving the ability of the aircraft to withstand the man-made hostile environment[1].During World War II no great improvements were made in this field.Combat survivability began to be considered a key feature in the design of platforms in the early‘70s,during the Cold War conflict in Southeast Asia.The heavy losses suffered in that period,mainly caused by a substantial shift from a formerly low-level threat environment to a higher intensity one,posed the base for a more rigorous approach to vulnerability.That new approach drove the development of new systems:for instance,the design of the AH-64 and the A-10 systems showed a clear aim to include vulnerability as primary task in the design philosophy[2—4].Survivability and vulnerability concepts became even more important in the‘80s.For instance,in 1984 the Department of Defense Survivability/Vulnerability Information Analysis Center(SURVIAC)was formed as a tool for supporting the survivability community in the technical area of nonnuclear survivability[5].Nowadays,military aircraft and platforms in general are commonly designed enhancing their survivability features,consequently leading to the improved ability to protect the occupants and to achieve their mission.More recently,in the 21st century,the survivability enhancing politics carried out by the U.S.Air Force led to the birth of the Joint Strike Fighter program,better known as the F-35 aircraft[1].Note that survivability concepts not only are usedwithin the aeronautical field,but they are also commonly adopted in the design phase of any kind of platform which is likely to be subjected to any external,impacting threat.For instance,ship design is an established example of survivability-driven practice[6].Hence,performing survivability assessments of a platform at its design phase is paramount in order to achieve the lowest kill probability resulting from an encounter with a threat.In this framework,both susceptibility and vulnerability assessments are pursued by designers.Yet,this work only focuses on the vulnerability assessment framework.The interested reader is referred to the works in Refs.[7,8]to go deeper into the implementation of computational environments dedicated to susceptibility.
The concept of survivability was first formalized by R.Ball in 1985 in its seminal work on combat aircraft survivability[1].He introduces some concepts for the design of fixed and rotary-wing aircraft with increased survivability features.Some of these ideas were further investigated in Ref.[9],which was intended as a review and application of the vulnerability reduction methods presented by Ball to long-range Strike Fighter aircraft.Similarly,the general methodology to conduct detailed single hit vulnerability assessments of generic aircraft at the conceptual design stage was presented in Ref.[10],based on the previous work by Ball.Since survivability analysis is usually statistically approached,a large amount of data is required to check the effect of one or more selected threats interacting with the system from different views.Therefore,many computer programs implementing the modelling techniques and computations at the base of vulnerability assessments were developed,as for instance the FASTGEN and the COVART software packages[11,12].The FASTGEN software implemented a shotline-based procedure,which,fed as input to the COVART software,allowed to determine the presented and vulnerable areas of the platform involved in the assessment.The vulnerable area is an index which allows identifying the vulnerability importance of the critical components in the platform.Even though the vulnerable area is the most consolidated importance measure considered in vulnerability analyses relying on the shotline procedure,it is not the only one in the field of vulnerability.For a deeper insight into the topic of important measures,the interested reader is referred to the works in Refs.[13,14].It is worth mentioning that the shotline procedure was not invented ad hoc for this kind of application,but it was inherited from the more general,consolidated algorithms of ray tracing.That class of algorithms was first described in 1968 with the purpose of studying the distribution of early reflected sound over the audience areas in concert halls of different shapes[15].In 1980 a refined ray-tracing algorithm was developed to render 3D scenes accounting for light reflections,refraction and shadows[16].Nowadays,these types of algorithms are even more advanced and,when coupled with stateof-the-art dedicated hardware,allow obtaining real-time raytracing performances in complex dynamic scenes[17].The vulnerability concepts pioneered by Ball were further investigated in Ref.[18],which introduced the equivalent target method to assess the single hit vulnerability of generic aircraft.This work successfully provided a computerizable calculation model,based on the shotline scanning method,offering the capability of accounting for the threat state-of-motion during the penetration process,even though in a simplistic way.The same authors later refined the shotline method and introduced the platform kill state evaluation to assess the overall kill probability of aircraft in a single hit scenario,by considering the eventual overlap between components[19].In Ref.[20]a direct simulation method to assess the multiple-hit vulnerability of aircraft with overlapping components was presented,based on the Monte Carlo simulations statistical framework proposed in Ref.[21].This methodology allowed to solve the combinatorial explosion problem typical of the implementation of the exact Markov Chain method,and to avoid the complex vulnerable area decomposition issue,which was described in Ref.[22].This method for conducting multi-hit assessments required to perform the identification and enumeration of all the possible exist states of the aircraft(e.g.kill state,nonkill state,redundant state[21]),which may be a heavy task when manually performed.Hence,to solve this issue,a Kronecker product method-based procedure was introduced to automatically enumerate the exist states of the platform[23].A detailed methodology to perform the vulnerability assessment of military aircraft in multiple-hit scenarios involving fragmentation warheads was discussed in Ref.[24].The methodology consisted in evaluating the characteristics of the missile fragments,e.g.,their dispersion,in determining the hit locations,the penetration of each fragment into the target components and,finally,the overall kill probability of the aircraft using the associated fault tree.Moreover,a kill criterion for the fuel tank eventual explosion was also considered to compute the platform vulnerability.In a later work by the same authors,the proposed framework was enhanced with the important concept of mean volume of effectiveness of the warhead[25].However,no mention of the damage due to the blast wave originated from the detonation of the high explosive material included in the missile core was reported.The inclusion of this damage mechanism into the analysis was presented more recently in Ref.[26],which refined the preliminary investigation of the blast event proposed in Ref.[1],allowing determining the kill state of the platform by modelling and assessing the structural vibration of the aircraft components within the elastoplastic framework,considering the force model in the plastic stage in a second step.However,only a maximum allowable displacement kill criterion was considered to determine the kill probability of the target due to blast loads.It is worth noting that not only projectiles and warheads have been evaluated as possible threats to aircraft platforms.For instance,the shotline scanning method was employed to compute the vulnerability of an unmanned platform to high-energy laser weapons[27].
Yet,only simplified methods are typically employed in survivability analyses to characterize the threat penetration mechanism.In fact,to the authors’best knowledge,only empirical simplified approaches have been considered to that purpose.At present,several methods offer a better description of the penetration capability of ballistic impactors.Terminal ballistic is currently widely investigated also in terms of modelling approaches.Considering the peculiarity of survivability/vulnerability analyses,a trade-off between accuracy and efficiency is required.Analytical methods that describe the penetration mechanism and features with a complete physical background,generally limited to simple shape targets,are fit for purpose.These models have been widely studied in the last decades and have been recently investigated by the authors.They allow predicting the impactor residual velocity or the eventual arrest for metal,composite and ceramic target materials considering low medium caliber threats,also including the deformation of soft-core bullets[28—31].
Survivability concepts not only are restricted to aircraft-based applications,but they can be easily extended to a wide variety of different fields involving structural safety and security with respect to impacting threats.For example,a shotline scanning method to assess the vulnerability of a ground combat vehicle was proposed in Ref.[32],considering both the target functional modelling and the fault tree analysis to determine the kill probability of the platform.The same terrestrial platform was also considered in Ref.[33],which presented numerous damage scenarios of components,created and classified according to damage types.Moreover,it also introduced a refined damage probability estimation algorithm accounting for the threat penetration process,including the evaluation of the eventual ricochet and deflection of the penetrator.Among the large number of security-related applications,it is worth mentioning the work that introduced a quantitative risk and resilience analysis of passive protection measures installed on critical assets[34].Furthermore,a management methodology to reduce the vulnerability of people within and close to these assets was also reported.Within the vulnerability analysis,the authors considered several types of threats,i.e.,impacting mortar,rocket and artillery threats.Finally,it is worth noting that,even though todate vulnerability analyses have been performed in the military domain and in some security-related fields only,some effort has been spent in the last years to extend such considerations to civil applications.For instance,preliminary studies to extend survivability considerations to the civil aviation domain were reported in Refs.[35,36],which investigate(i)collisions with unmanned systems and bird strikes and(ii)the survivability of the public in case of collision of the platform on the ground.
Moreover,to the authors'best knowledge,few applications to helicopter platforms have been recently investigated in the survivability field in an exhaustive way.This kind of investigation would be of paramount importance and significantly interesting,since helicopters experience numerous flight conditions exposing the system to different types of threats.Among the few works published on the topic,it is worth highlighting the work published in 1987 that studied the single hit vulnerability of a combat helicopter primarily focusing on the identification of critical components[37].However,due to the complexity of the helicopter platform and with the aim of showing simple examples of vulnerability computations,these were performed by hand considering three shotlines only and neglecting any projectile penetration mechanism into the target.The topic was also dealt with in Ref.[38],which presented a generic overview of the helicopters vulnerability assessment and reduction techniques framework.It was reported there that,in the early use of helicopters on the battlefield,the survivability enhancing tactics were to fly high enough in order to be out of the range of small arms,i.e.,generally around 3000 ft.With the advent of shoulder missile launchers in the late’60s,updated strategies had to be developed,resulting in helicopters flying at a lower level,with the drawback of increasing the probability of being impacted by small arms projectiles.As a consequence,a higher degree of ballistic tolerance had to be pursued in the design phase of such systems.However,during the close-to-the-ground hovering phase,helicopters are still susceptible and vulnerable to projectiles fired by small arms.
In this context,this work has the aim of(i)establishing the general framework in which a vulnerability assessment may be performed and of(ii)presenting the in-house software implementing it.Moreover,special attention is paid to the description of the capability of accounting for the threat penetration into the target,which is considered an innovative feature in the vulnerability field.The focus of the paper is mainly on the“ballistic”vulnerability,but the framework is flexible enough to be used also with different type of threats.
The paper is organized as follows.In Section 2,the general framework to determine the vulnerability of a platform is presented,with the focus on single hits from small arms projectile threats.Even if the framework is based on the classical procedure described by Ball[1],several novel aspects are introduced.An example of assessment is then developed step by step in Section 3,which considers a military helicopter platform.Finally,Section 4 gives the conclusions of this work.
2.Vulnerability assessment general overview
This Section provides the general framework and the operative procedure for the vulnerability assessment of a generic platform subjected to impacting threats.Note that reference is mainly made to aeronautical examples,since this is the traditional field of applicability of survivability concepts,but the validity of the approach is quite broad.The threat considered herein is represented by small/medium caliber kinetic energy projectiles.An inhouse software package implementing the algorithms described in this Section is employed in Section 3,in which a hands-on application on a military helicopter platform is presented.To this purpose,a simplified and available model loosely based on an actual Bell AH-1 Cobra helicopter is considered[39].However,the aim of the authors is not to provide results for a particular helicopter,but to simply use this model to demonstrate the in-house software package capabilities.
It is worth introducing the basic terminology adopted in this study.The elementary entities the platform is composed of are referred to as components.For instance,the engine and the blades of the aircraft are components of that platform.Redundant components are identified with the term group of redundant components.A set of components working together to achieve a common goal is identified with the term system.An example of system in a helicopter is the main rotor drive,which includes components such as the satellite gears,the collector gears,etc.Finally,the term platform identifies the aircraft itself,which can be described as the combination of all the identified systems.
Before passing to the operational framework,the phases in which vulnerability,and more in general survivability,are usually considered in the development of a project are here formally defined.Note that this schematic organization of the project phases is introduced in this work combining fragmented pieces of information recovered from different works.Some survivability-related requirements first appear in two coordinated documents,i.e.,the Initial Capabilities Document(ICD)and the Systems Engineering Plan(SEP).The ICD is intended as a mean to fill the gap between initial capabilities and expectations,while the SEP represents an exhaustive list of technical aspects-related information of the program,from conception to disposal[40].The survivabilityrelated requirements reported in these two documents are verified employing vulnerability assessments,which in this context are typically performed gathering information from experimental tests and using it inside numerical frameworks.Interestingly,the military standard MIL-STD-2069[41],which was published in 1961 and substituted by the more recent MIL-HDBK-2069 in 1997,already reported the possibility of performing vulnerability evaluations on aircraft with computer programs,such as SHOTGEN/FASTGEN or MAGIC.It is worth mentioning that these computer programs started being developed in the late‘60s with the purpose of performing analyses involving the description(commonly called shotline description)of the target penetration process employing a series of parallel lines[11].Vulnerability assessments shall be effectively iterated during platform design,development and production[41].Moreover,such vulnerability analyses may also be exploited throughout the operational life of a platform,with the purpose of evaluating changes in missions,tactics,threat configurations and upgrades of the platforms[41].
2.1.Vulnerability assessment to projectiles—framework overview
In order to perform a vulnerability assessment,the platform,the threat and their mutual interaction have to be described.The platform description involves the model setup and the specification of the systems considered in the analysis and of the critical components.These are usually identified through a Fault Tree Analysis(FTA),which also allows identifying eventual redundancies to consider for a realistic assessment.The criteria underlying the selection of the critical components are defined in a preliminaryphase,according to the mission failure definition(attrition kill level)selected for the assessment.The interested reader is invited to read the work in Ref.[42]for further details on this topic.The threat description process depends on the type of threat selected for the assessment.In this Section,high penetration armor-piercing(AP)projectiles are considered.Hence,velocity,trajectory and projectile type need to be specified.Additionally,the mutual interaction between the threat and the target must be introduced,which is later used to determine the penetration depth within each critical component.
The vulnerability assessment general procedure consists of the five subsequent steps identified in the block diagram of Fig.1.Each step is discussed in detail in the following.
2.1.1.Pre-processing phase
The first step to perform in the Pre-processing phase is the selection of the attrition kill level for the current vulnerability assessment,which is usually based on the criteria reported in the literature available on the topic,e.g.,Refs.[1,41].It forms the basis for the critical components selection procedure,commonly named Critical Component Analysis[1],which is aimed at determining what makes the aircraft vulnerable.Therefore,first the vulnerable components,along with their kill modes,have to be identified,typically by the analysis of combat data(when available for previous versions and/or similar aircraft)and by testing the components,the systems and the full-up aircraft.The Critical Component Analysis phase ends with the establishment of the platform kill tree through a Fault Tree Analysis,which also allows determining the systems the platform is composed of,each of which contains the respective critical components previously identified.No further details are reported about the pre-processing phase since this is not the main focus of this work.The interested reader is referred to Ball's work for a deeper insight into this topic[1].
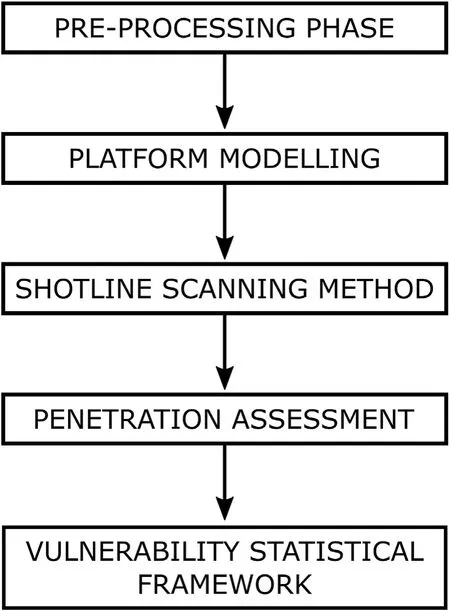
Fig.1.Vulnerability assessment to projectiles-general framework.
2.1.2.Platform modelling
The platform critical components selected during the Critical Components Analysis have to be modelled and fed as input to the general vulnerability framework,along with the information about the systems they belong to,eventual redundancies and the materials they are made of.These models should be accurate enough to achieve reliable results,but,at the same time,they have to be(i)efficient in terms of computational costs,to allow performing several iterative runs for optimization purposes and(ii)schematic,since vulnerability analyses are frequently carried out in a preliminary stage of the project,when not all the systems have been fully defined yet.These requirements are met in this work exploiting simple geometric models to which some additional specifiers are associated in the form of metadata.
The geometric models of the critical components should be simplified versions of the real counterparts,eventually reduced to simple geometric shapes,such as cubes or cylinders.Specifically,in this work the STL format,which consists of triangles covering the surfaces of the modelled part,is suggested for the 3D models.This specific choice is made because it provides an accurate representation of objects without producing large-sized files.Note that the more complex the object surfaces to describe are,the more triangles are required,thus leading to increased computational times for the vulnerability assessment analysis.The simplified model must guarantee the same encumbrance and mass of the original object it describes to represent the effects of the selected threat on the real component with an acceptable level of approximation.The main parameters driving the penetration mechanism(the only damage process assessed in this work)are considered in an approximate,but engineering-sound fashion.This is achieved by building simple hollow shapes with an appropriate wall thickness which allows fulfilling the aforementioned requirements.For instance,consider a structure such as an engine simplified as a cylinder.The simplification procedure is performed in two steps:
1)The first step consists of modelling the cylinder so that it wraps the original object:this procedure guarantees the encumbrance conservation.
2)The second step is aimed at determining the wall thickness t that fulfils the mass conservation requirement.
The real engine and its corresponding simplified model are shown in Fig.2,where the engine of the helicopter tested in Section 3 is used to demonstrate the whole procedure.It is worth noting that the level of simplification may be decided as a function of the level of details in the systems and subsystems required by the analyses.
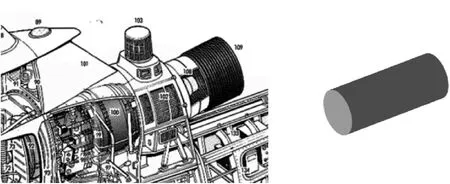
Fig.2.Modelling of the engine component-cutaway[43](left)and simplified version(right).
2.1.3.Shotline scanning method
Before conducting a vulnerability assessment,all the possible directions of the incoming threat must be selected.Typically,a sphere around the center of the platform is chosen,meaning the threats may come from any possible direction,or only a spherical sector of it is considered,in case a limited range of threat directions are to be assessed.Hence,it is suitable to define the threat trajectory in terms of azimuth and elevation angles,which may be defined with respect to the platform model reference system,as shown in Fig.3(a)and(b)for the azimuth and elevation angle,respectively.A specific combination of azimuth and elevation angles is referred to as an aspect.During the vulnerability assessment,each selected aspect is analyzed by means of the shotline scanning method.
For each specific aspect considered,the projection of all the models of the critical components on the plane perpendicular to the vector defined by that aspect is determined,and a shotlines grid is superimposed on it.The grid generation process consists of two steps:
1)The grid edges are placed to include the whole projection(shade)of the model(Fig.4(a)).
2)The grid is divided into identical square cells(Fig.4(b)),whose dimension(s)has to be accurately determined by means of a sensitivity analysis aimed at determining an acceptable tradeoff between the computational cost and the accuracy of the vulnerability assessment results.
A shotline perpendicular to the grid plane is generated inside each cell in a generic point,along the threat trajectory.The geometric center of each cell is used in the method considered in this work.
A ray tracing algorithm is implemented with the purpose of determining the triangles intercepted by each shotline.The algorithm considered in this paper is composed of two steps:
1)The intersection point between the current shotline and the plane on which the current triangle lies is determined.
2)The eventual intersection is assessed identifying if the calculated intersection point lies inside the current triangle.
The procedure is schematized in Fig.5 for a simplified scenario,where a shotline intercepting one triangle(left)and one missing it(right)are shown.
For each shotline,this two-steps ray tracing procedure is performed considering every triangle on the surface of the critical components 3D models.The shotlines that do not intersect any component are discarded,whereas those hitting at least one triangle are stored.For each stored shotline the complete list of the intercepted components is determined and written in a structure variable,which is referred to as partial shotline hit sequence.The variable also collects,for each reported component,the relative hit point coordinates,impact angle and perpendicular distance of the hit point from the shotlines grid plane.
Note that,due to the low thickness of the helicopter skin,the skin is neither critical nor effective in slowing down any incipient threat.However,the skin component must still be considered in the assessment,since it greatly contributes to the total presented area of the platform in each specific aspect considered,which is required for the kill probabilities calculation.
2.1.4.Penetration assessment
One of the key aspects of the threat-structure interaction is that the projectile penetration capability is progressively reduced as it hits the components along its trajectory.The accurate evaluation of this phenomenon is a novel aspect in the survivability research field and is paramount when it comes to helicopter vulnerability assessments,especially in view of the fact that helicopters are the only aerial platforms able to perform close-to-the-ground hovering phases,during which projectiles fired by small arms become hazardous threats.Hence,performing penetration assessment may be vital to determine realistic vulnerability values.Small caliberbullets may,in fact,progressively be arrested by the first encountered components,thus preserving the integrity of the inner ones.In order to take this phenomenon into account,the proposed framework employs accurate penetration algorithms to evaluate the progressive velocity loss of the projectile.These algorithms have already been investigated by the authors and allow the prediction of the impactor residual velocity,or the eventual complete arrest,for a wide variety of target materials:metals,composite and ceramic[28—31].These models are based on analytic solutions and allow a relatively fast,but accurate,prediction of the penetration capability of low-medium caliber threats,including also the deformation of the bullet for soft core ones.However,to further speed up the vulnerability analyses,it is recommended to a priori analyze the behavior of the selected threat with respect to the impacted materials.This task can be achieved using the analytical impact software to calculate the Recht-Ipson curves[44]for each threat and material,considering different thickness values of the component hit.These curves provide a reasonable estimation of the residual velocity of a threat after impacting and penetrating a target material,as a function of the impact velocity,thus allowing fast assessment of the residual perforation capability.The equation governing the residual velocity of the projectile is given by Eq.(1)[28—31]:
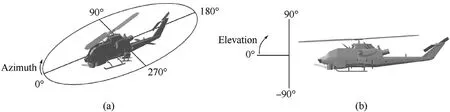
Fig.3.Aspect definition-azimuth angle(a)and elevation angle(b).
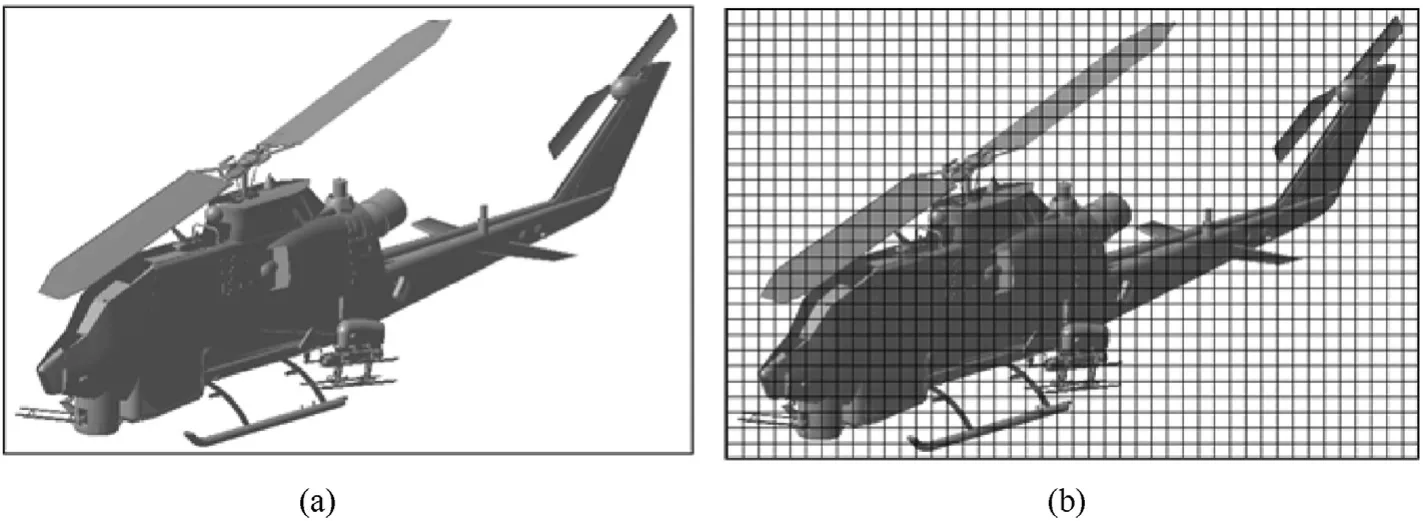
Fig.4.Shotlines grid generation.(a)shows the placement of the grid edges,while in(b)the grid is divided into identical square cells.
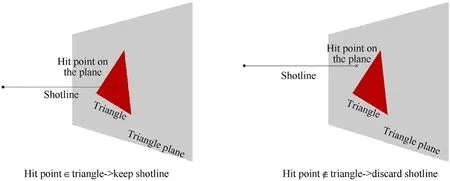
Fig.5.Ray tracing algorithm possible outcomes.
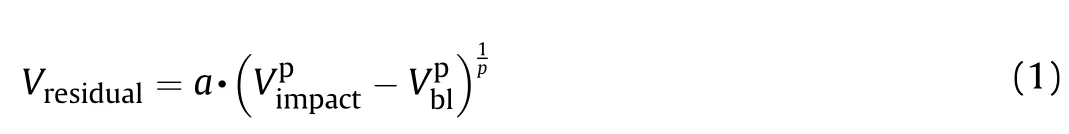
where a and p are fitting parameters,Vis the impact velocity and Vthe ballistic limit velocity.
In this work,such curves are obtained,for each target materialprojectile couple,at some relevant values of the target thickness,using the procedure described in Refs.[28—31].This procedure,given the projectile and target parameters,allows assessing if a complete target perforation occurs and,in this case,it provides the residual velocity of the projectile.The thickness range selected in this work for the computations is defined by a lower limit equal to 1 mm and an upper limit identified as the minimum thickness required to completely stop the threat.Note that the definition of a lower limit implies that every material thickness lower than that value lets the projectile go through without reducing its flight velocity.The analyses provide for each target material—threat combination considered the curve relating the impact velocity and the residual velocity of the eventual threat.Each curve is then fit with Eq.(1)to determine the parameters a and p.An example of Recht-Ipson curve is shown in Fig.6.
For each shotline,the information regarding all the intercepted components is included in the partial shotline hit sequence.Thepenetration algorithm works according to a two-steps procedure:
Fig.6.Recht-Ipson curve example for threat 12.7 x 99 API M8 bullet and Kevlar 29—epoxy plate employing the analytical modelling approach[29].
1)Identification of the penetration distance(t)inside a component.
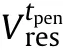
The penetration distance is determined as the distance between the entry point into and the exit point from the current component.Note that a component may be intercepted more than once,as in complex geometric shapes or hollow models.In these cases,a penetration assessment is performed for each intercepted thickness identified.During step 1,if the impact velocity is lower than the Ballistic Limit velocity of the current target—projectile couple,the projectile is stopped and so is the shotline.If,instead,the Ballistic Limit velocity is lower than the impact velocity,step 2 is performed and the residual velocity after the complete penetration is computed by means of Eq.(2)[28—31]:
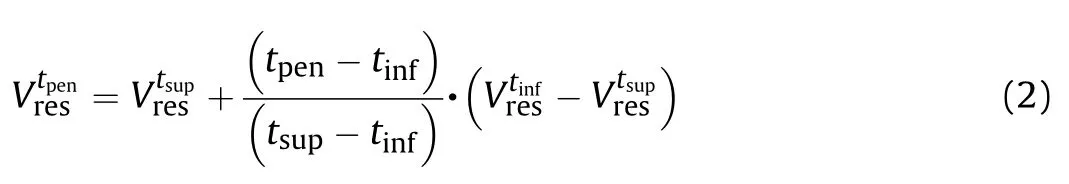
where tand tidentify the thickness values immediately larger and smaller than tavailable in the database,respectively,while Vis the residual velocity of the same projectile penetrating a component with thickness t made of the same target material.In case of complete penetration of the current component,the twosteps procedure is repeated with the next instance reported in the partial shotline hit sequence.If,instead,the projectile is stopped,the penetration algorithm proceeds to the next shotline.
Note that the whole methodology proposed above cannot describe,in the current state,the secondary effects of the penetration of projectiles,such as spallation and projectile fragmentation,which,according to the authors’best knowledge,are known to have limited effects on helicopter structures and systems hit by Armor Piercing(AP)projectiles[45].Differently,these phenomena may be somehow taken into account when assessing the vulnerability of different types of platforms,such as tanks,and when considering specific threats,such as High Explosive Squash Heads(HESHs).
2.1.5.Vulnerability statistical framework
This Section only aims to introduce the vulnerability statistical framework implemented in the methodology proposed in this work,without focusing on the specific equations and procedures involved in the computations.Such equations are fully reported in Appendix A,where,in addition to the classical method suggested by Ball[1],two refined algorithms are presented for the assessment of the kill probabilities of systems and groups of redundant components.

The whole procedure to conduct a vulnerability assessment is schematized in detail in Table 1.
3.Case study
This Section presents a hands-on application of the general approach discussed above.All the phases of the vulnerability assessment,which are reported in Table 1,are considered step by step.The platform considered herein is a helicopter inspired to the Bell AH-1 Cobra.For the sake of clarity,note that the following analysis is not intended as an actual vulnerability assessment of the real version of the helicopter,but,rather,as a demonstration of the approach presented in this work.
The threat considered in this vulnerability assessment is represented by the 7.62×54 API B-32 projectile,but other types of projectiles can be easily implemented exploiting the penetration software packages[28—31].API stands for Armor Piercing Incendiary,which identifies special bullets with incendiary capability.For simplicity,the only penetration capability is considered in this work,neglecting the effect of the incendiary potential.The impact velocity is assumed to be equal to 830 m/s,which is a typical value for the flight velocity of the selected threat[46].
3.1.Pre-processing phase and platform modelling
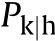
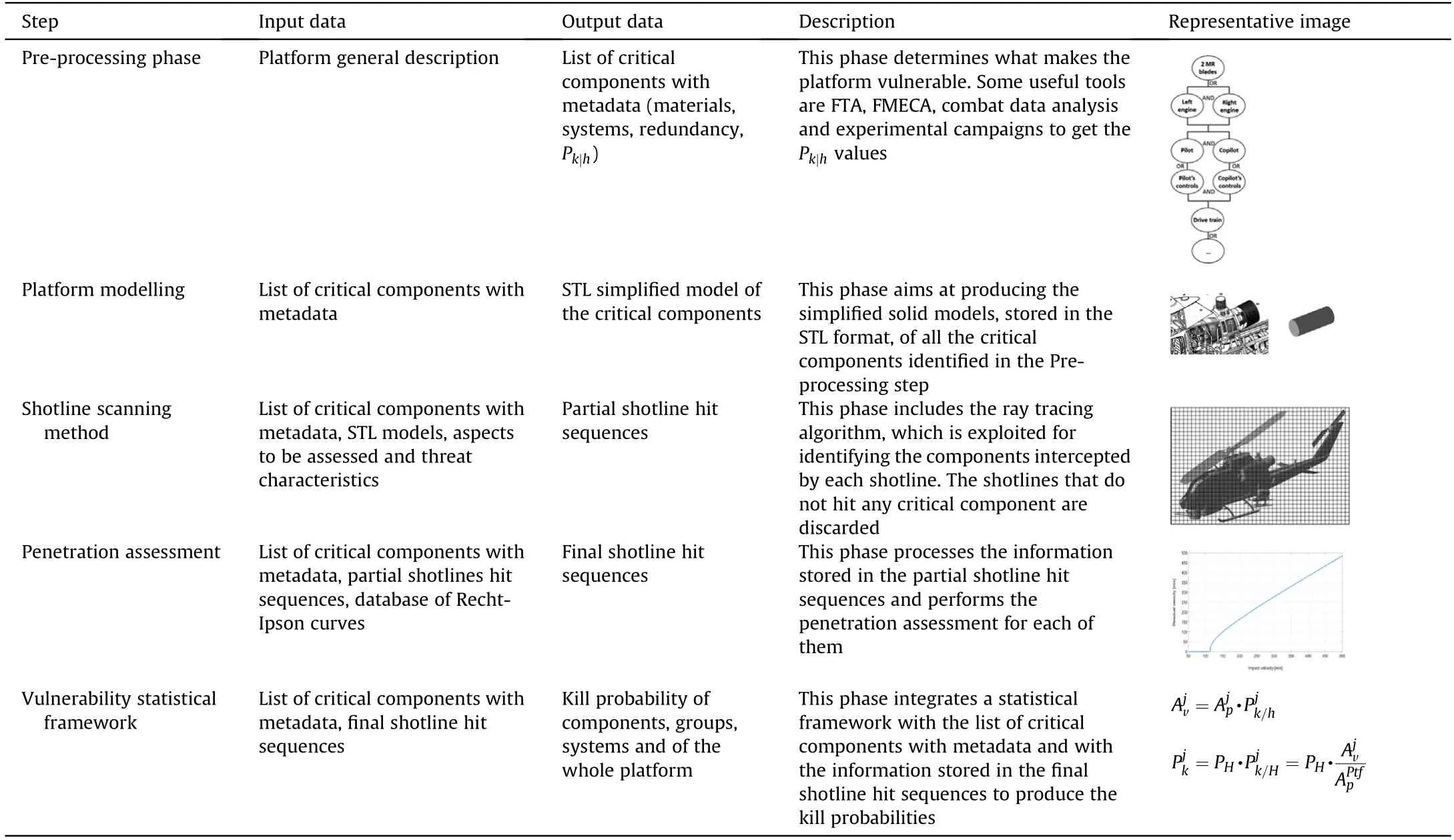
Table 1Detailed procedure of a generic vulnerability assessment.
The complete platform considered in this assessment is shown in Fig.7.
3.2.Shotline scanning method
The aspects considered in this assessment are determined by combining azimuth angles in the range[0,350],with a step of 10,with elevation angles in the range[-90,50],with the same step of 10.The reference system for the definition of the azimuth and elevation angles has already been shown in Fig.3.
The cell size to be used in the shotline scanning method is determined by means of a sensitivity analysis.Since the smallest relevant dimension of the tiniest component considered in this assessment is 10 mm,some relevant cell sizes are considered,i.e.,from 5 mm up to 200 mm with a 5 mm step.The vulnerability value of the whole platform is computed,considering each cell size,at three aspects,namely(az,el)=(0,0),(az,el)=(90,0)and(az,el)=(40,40).For each aspect,the percentage error(e%)between the vulnerability value with the smallest cell size and the other cell sizes is computed.According to experience,the convergence threshold is set to |e%|=1%.The main outcomes of this sensitivity analysis,i.e.,the computational time and the percentage error,are reported in Fig.8 for the only aspect(0,0),which turns out to be the aspect requiring the smallest mesh size to reach convergence.Note that no information is presented for the other aspects considered in the convergence analysis,since they show a similar behavior as the one reported in Fig.8 and require less restrictive mesh size to reach convergence.According to the convergence criterion,cell sizes up to 40 mm may be accepted in all the aspects analyzed.Hence,a grid size of 25 mm is selected as an acceptable trade-off between the accuracy of the results and the time required for the analysis.It is worth mentioning that the sensitivity analysis of vulnerability assessments shows different behavior from the one observed in usual convergence analysis.In fact,as it can be seen in Fig.8,the error value keeps oscillating between positive and negative values as the mesh size increases.This oscillatory behavior is usually shown when the mesh size adopted is the same order of magnitude of the size of the components and is also influenced by the arrangement of the components inside the platform.This implies that some large cell size values may still provide an error within the acceptance threshold for convergence,looking at a single aspect,still not guaranteeing convergence in the other aspects.This is the case of the mesh size 70 mm,which in the aspect(0,0)shows an error|e%|=0˙69% with respect to the smallest mesh size considered.Thus,to avoid this issue,many aspects have to be considered to determine the acceptable mesh size.The selection of these aspects may be performed according to experience by identifying the most critical combinations of azimuth and elevation angles.Moreover,the cell size guaranteeing convergence is platform-dependent,since it is strictly related to the minimum size of the tiniest component considered in the analysis.Hence,it is suggested to perform this kind of sensitivity analysis each time a new platform needs to be assessed.
For each considered aspect,the shotline scanning methodoutputs a partial shotline hit sequence for each shotline that intersects at least one critical component.A shotline in the aspect(0,0),which is shown in Fig.9,is selected to show an example of such a structure variable(Table 3).
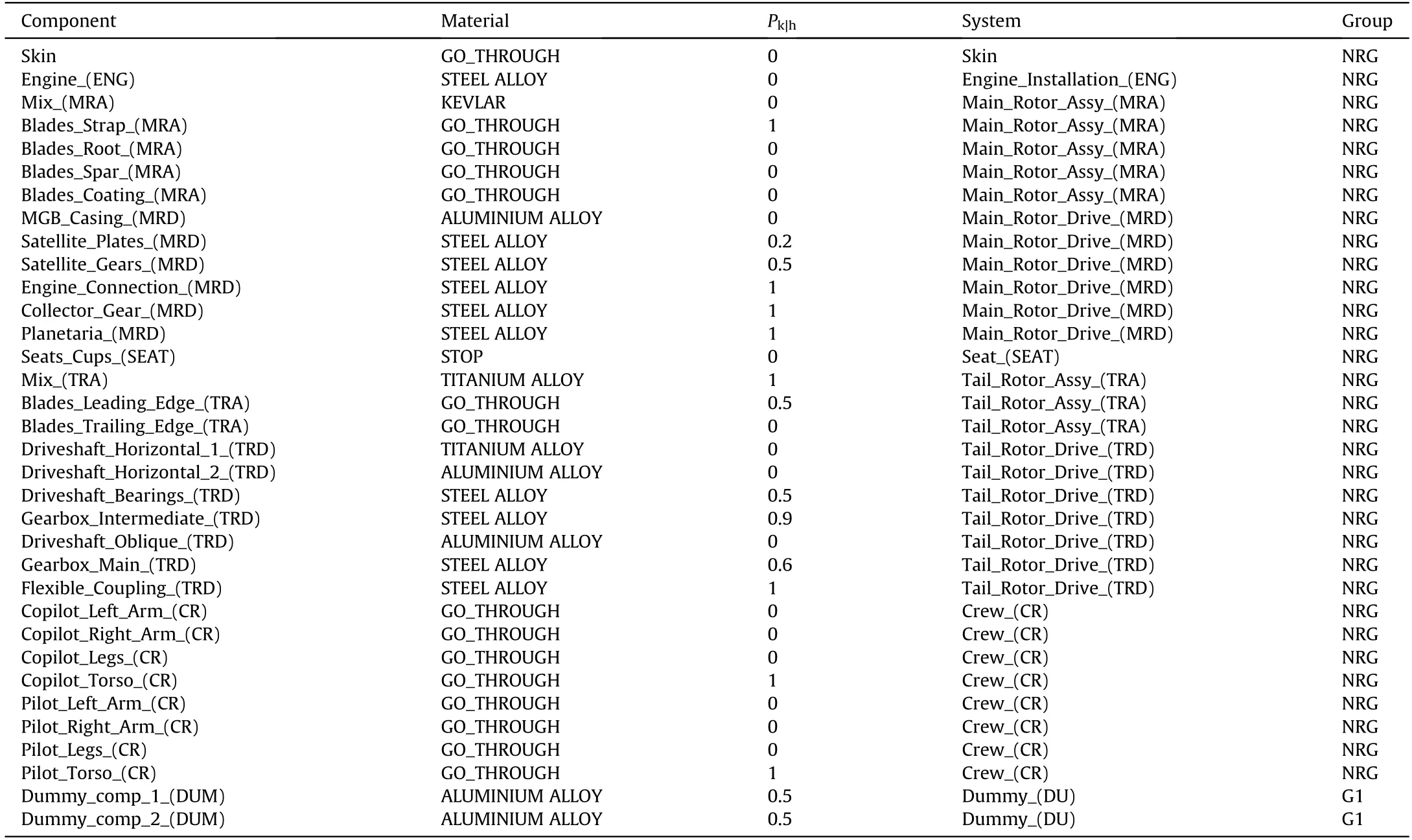
Table 2Components considered in the vulnerability assessment.
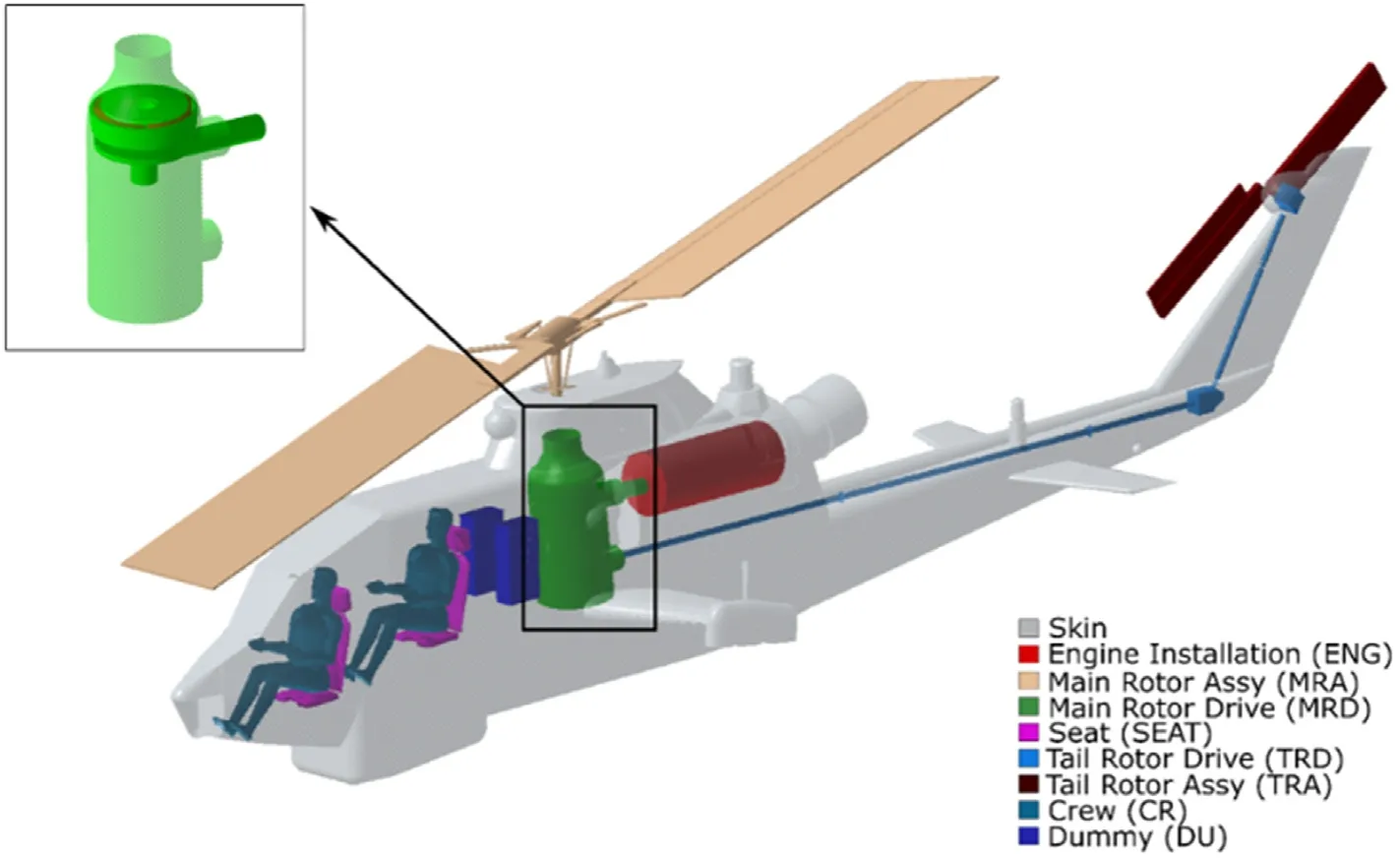
Fig.7.Platform considered in the case study.The different colors identify the systems considered in the assessment.
The partial shotline hit sequence lists all the intercepted components sorted from the first to the last intercepted one(column 1),the hit point location in mm(column 2),the impact angle in degrees(column 3)and the hit point distance,in mm,from the shotlines grid(column 4).In the example reported above,the penetrator hits the skin of the helicopter first,then it enters the platform and intercepts the pilot torso(Pilot_Torso_CR),the main gearbox casing(MGB_Casing_MRD)and the engine component(Engine_ENG),before exiting through the skin again.
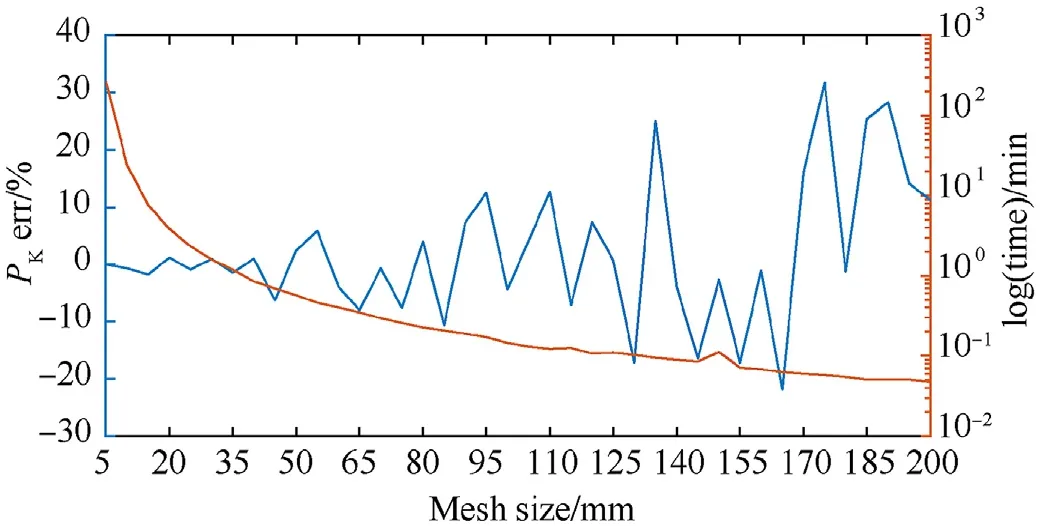
Fig.8.Sensitivity analysis results in the aspect(0°,0°).
3.3.Penetration assessment
The penetration assessment is performed using the database of Recht-Ipson curves implemented in the software package,which includes all the materials involved in the analysis and the selected threat.The input to this phase is the set of partial shotline hit sequences determined by the previous shotline scanning method in the current aspect.Each of these structure variables is processed by the penetration algorithm presented in Section 2,which evaluates the eventual loss of velocity of the penetrator as it flies through the intercepted components.The output of this phase is the list of the final shotline hit sequences in the current aspect.As an example,the fields of this structure variable that are not already reported in the partial shotline hit sequence are presented in Table 4 for the selected shotline in the aspect(0,0),along with the material of each intercepted component.
The final shotline hit sequence adds to the information stored in the corresponding partial shotline hit sequence the thickness of the intercepted wall in mm and the penetrator flight velocity in m/s at the corresponding hit point location.It is worth recalling that the wall thickness value of each intercepted component is computed along the projectile trajectory,this variable is sometimes referred to as line-of-sight thickness in the literature.Looking at the example shown in Table 4,according to the assumptions already reported in Section 2,the skin and the Pilot_Torso_CR components are penetrated by the threat without any effect on the flight velocity.In fact,since the projectile velocity decay caused by the penetration of these components is considered negligible compared to the speed reduction due to the interaction with the other thicker and stiffer components considered in the model,the skin and the Pilot_Torso_CR are assigned the material GO_THROUGH,which allows skipping the computation of the velocity decay.As the projectile continues along the shotline,it enters the MGB_Casing_MRD component trough a 6.45 mm thick wall,reducing its velocity from 830 m/s to 819 m/s,further slowing down to 808 m/s when exiting the component through a 6.45 mm thick wall.After that,the threat penetrates the 20.00 mm thick entrance wall of the engine component,which drastically reduces the projectile flight velocity to 372 m/s.Finally,the projectile is stopped while travelling through the exit wall of the engine.Hence,the last skin component reported in the partial shotline hit sequence in Table 3 is dropped and not reported any more in the final shotline hit sequence.The progressive velocity loss of the projectile is shown in Fig.10.Note that,as expected,the projectile velocity only decreases as it penetrates the entrance or the exit wall of a component,remaining constant inside it,due to the hollow geometry chosen to model the simplified components(see Section 2).
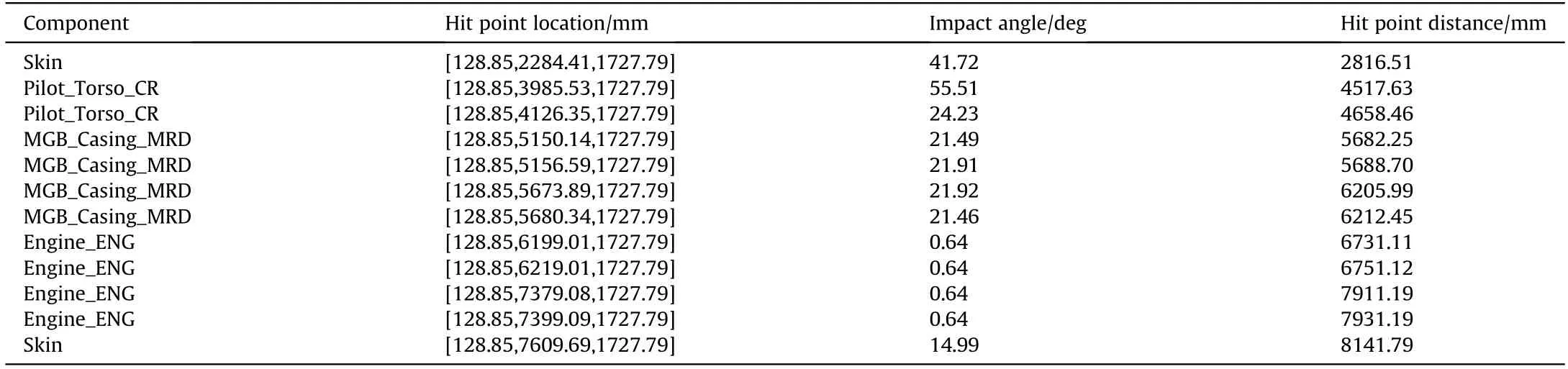
Table 3Partial shotline hit sequence for the selected shotline in the aspect(0°,0°).
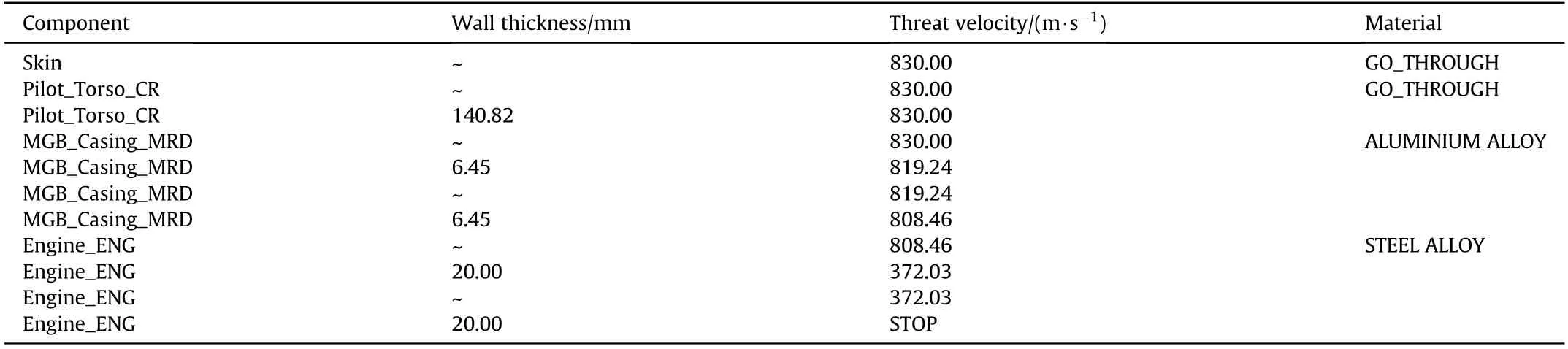
Table 4Final shotline hit sequence for the selected shotline in the aspect(0°,0°).
3.4.Vulnerability statistical framework
The statistical framework presented in Section 2 and in Appendix A is employed to determine the kill probability of the non-redundant critical components,the groups of redundant critical components and the systems in the platform,along with the global killability of the helicopter itself.
Fig.11 shows the 3D bar plot of the killability values of the helicopter considered in this case study.The highest values of the kill probability are obtained in the front aspects,i.e.,those around(0,0),with a peak value of approximately 14.3%.As the azimuth angle increases,a global killability reduction trend is observed up to the lateral aspects,i.e.,those around el=0and az=90.This is an expected behavior,since the lateral aspects are characterized by a total presented area greater than the front ones(Fig.12).Hence,intuitively,a projectile randomly hitting the aircraft profile anywhere at az=90has a lower possibility of intercepting a critical component than a threat flying along a path characterized by az=0.An increasing trend is then experienced moving to the rear aspects,i.e.,towards az=180,with a sudden reduction of the platform kill probability to a value of approximately 5.5% at az=180.This may be determined by the sudden reduction of the Crew_(CR)system kill probability in the aspects around az=180,since the seatcups stop most of the projectiles aimed at the crewmembers.Further considerations on the vulnerability of the systems are reported below resorting to 2D plots.Moreover,due to the quite perfect symmetry of the helicopter considered,the kill probability values are almost symmetric with respect to the rear aspect.Overall,the safest aspect is that characterized by(190,-60),at which P=3˙5%.
Yet,the 3D bar plot only captures the overall behavior of thevulnerability value of the aircraft.Therefore,2D plots may be more suitable to obtain a deeper insight into some specific aspects.
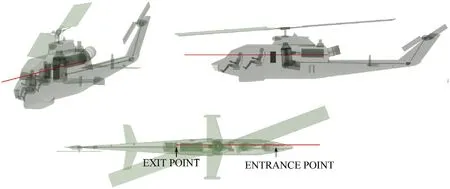
Fig.9.Example of the selected shotline in the aspect(0°,0°).
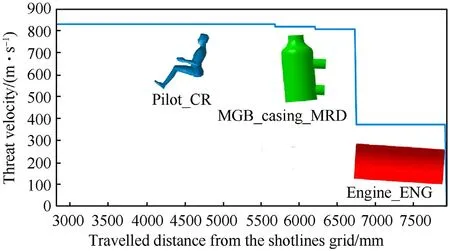
Fig.10.Projectile velocity reduction along the selected shotline in the aspect(0°,0°).
Fig.13(a and b)shows the 2D curves of the helicopter kill probability at all the aspects with(az=[0,350],el=0)and(az=0,el=[-90,50]),respectively.Fig.13(a)confirms that the front aspect(az=0,el=0)is the most critical one.This result is mainly determined by the high kill probability of the Crew_(CR)system in the front aspect,as shown in the 2D plot comparing the killability of each system at el=0(Fig.14(a)).This is expected,since the pilots are completely exposed to front shots,while they are protected by the seatcups in case of projectiles coming from rear aspects.The same conclusion can be given looking at Fig.13(b).In fact,the greatest kill probability value is determined at el=0.
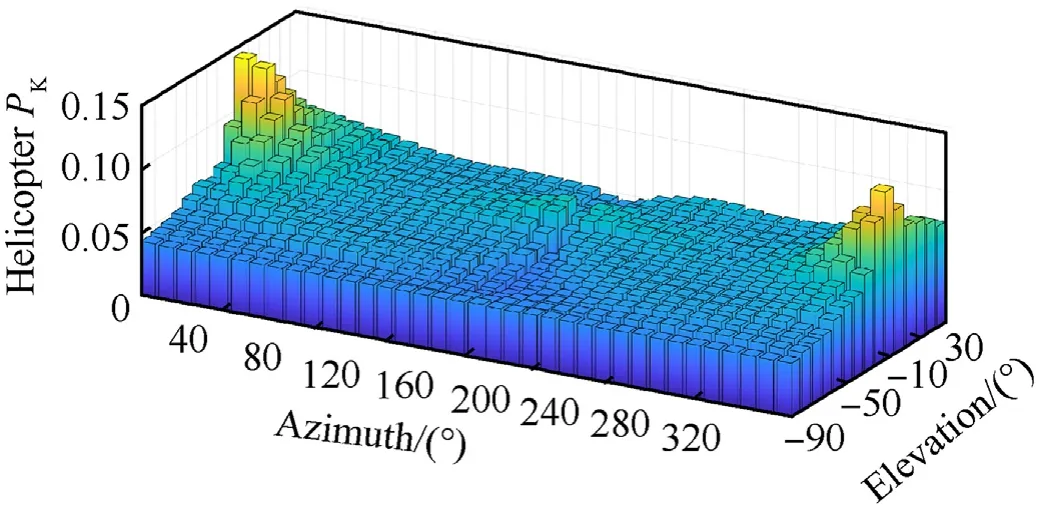
Fig.11.Platform killability-3D bar view.
The comparison of the behavior of the different systems may be in general useful to identify criticalities,possibly leading to the design of protection surfaces in an effort to increase the platform survivability.In the present case study,the most vulnerable system at el=0turns out to be the Crew_(CR)system,except from the aspects around az=180,where the Tail_Rotor_Drive_(TRD)system shows the worst survivability performance(Fig.14(a)).Moreover,Fig.14(a)clearly shows the sudden killability reduction of the Crew_(CR)system in the rear aspect.Conversely,at az=0,the Main_Rotor_Drive_(MRD)system is the most critical one up to el=-50,while the Crew_(CR)system still turns out to be the most likely to be killed in the other aspects considered(Fig.14(b)).
Finally,Fig.14 also shows the comparison of the Dummy_(DU)system killability with and without considering redundancy.As expected,it can be seen that redundancy significantly lowers the system kill probability,since both the Dummy_comp_1_(DUM)and Dummy_comp_2_(DUM)parts must be simultaneously hit by the same single shot to provide a non-null kill probability for the system they belong to.For instance,that is the case of the aspect(50,0),where the two redundant components only overlap by a little area,as show in Fig.15.However,even in case a specific aspect allows a complete overlap of the redundant parts,the killprobability of the overall system is still significantly lowered.This is due to the fact that,after being hit,all the redundant components must fail in order for the system to be killed.Conversely,the failure of at least one of the components is a sufficient condition for the system kill in case no redundancy is considered.This is the case of the aspect(90,0),where the two dummy components are always simultaneously hit by the threat,as show in Fig.15.Hence,both the two aspects shown in Fig.15 prove the advantage of including redundancy in the design of the platform.In fact,considering el=0,in the aspect characterized by az=50the Dummy_(DU)system kill probability is reduced from 1.3% without redundancy to 0.1% if redundancy is considered,while at az=90redundancy reduces the system killability value from 0.7% to 0.2%.

Fig.12.Total presented areas in the aspects(270°,0°)and(0°,0°).
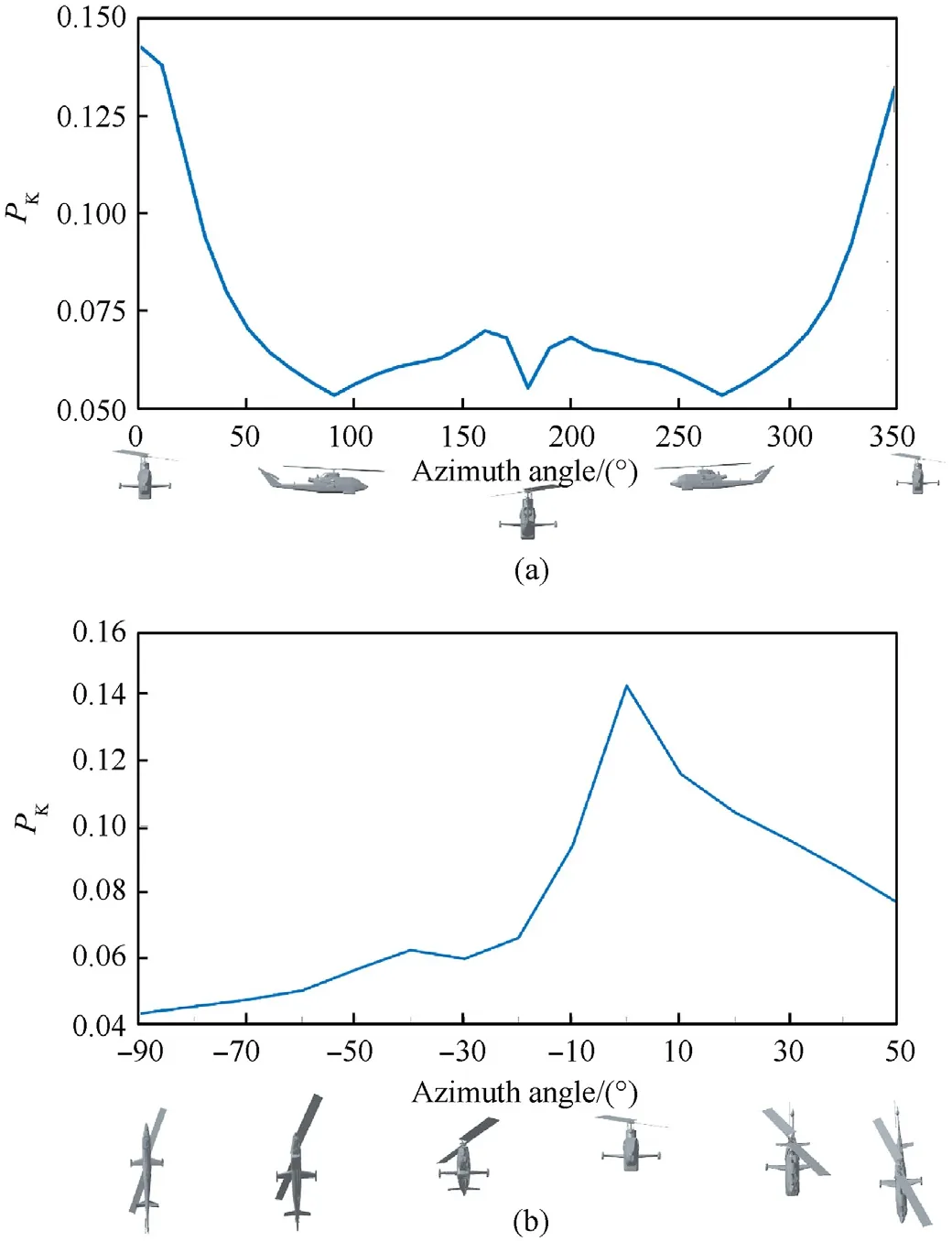
Fig.13.Platform killability-2D curve view at el=0°(a)and az=0°(b).
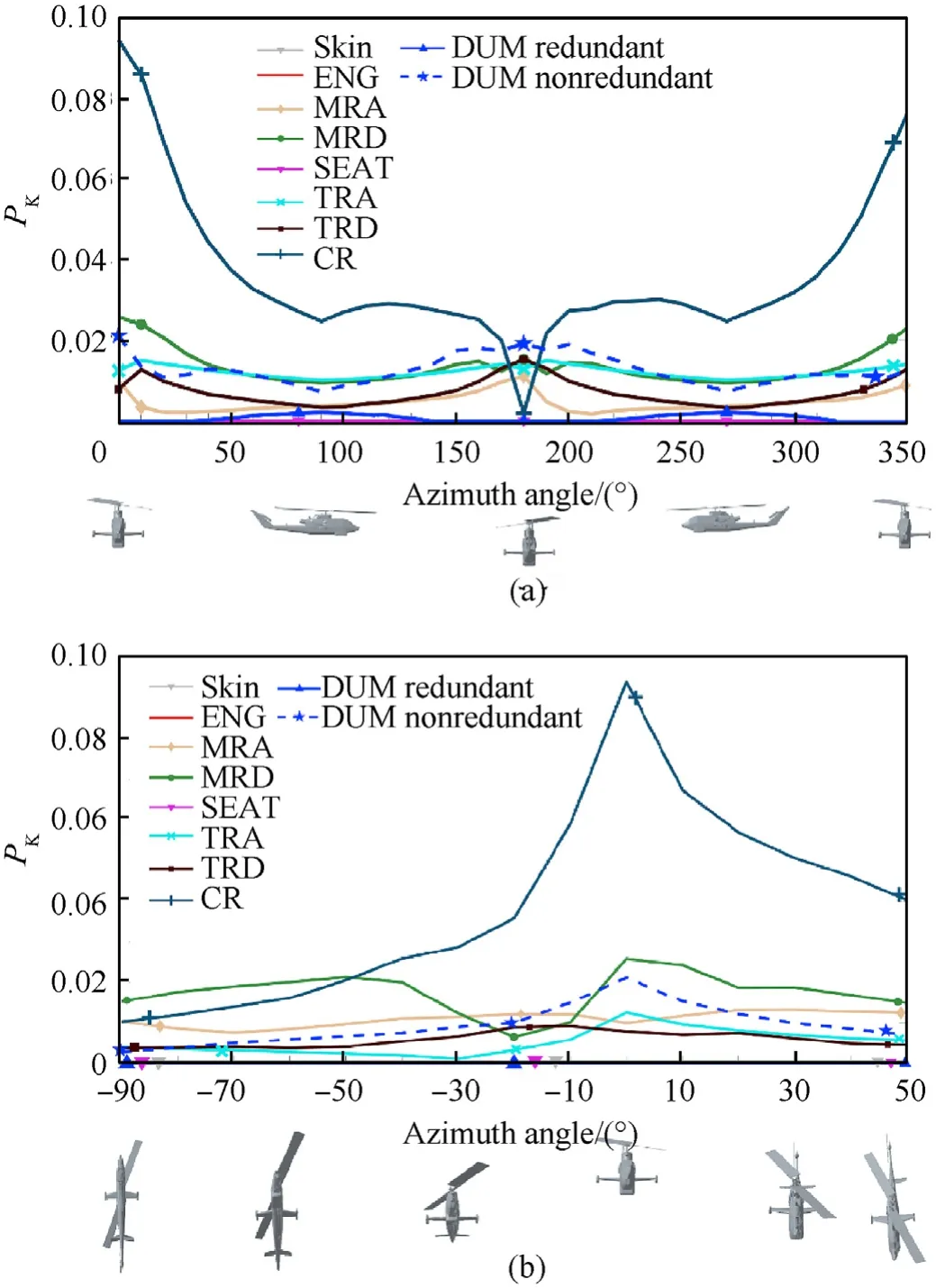
Fig.14.Systems killability-2D curves view at el=0°(a)and az=0°(b).
4.Conclusions
Survivability has progressively gained importance in the past decades,becoming a driving feature of the design of modern platforms.Therefore,it is paramount to establish a definitive general framework to assess the vulnerability of different types of platforms to any impacting threat of interest.This framework may be effective in the whole process of designing,producing or even upgrading a platform.
This work is aimed at providing the general framework to conduct vulnerability assessments of generic platforms,being them aerial,naval or terrestrial,to external impacting projectiles.The methodological approach proposed in this work is composed of fivedistinct subsequent phases:pre-processing,platform modelling,shotline scanning method,penetration assessment and vulnerability statistical framework.The pre-processing phase is mainly aimed at identifying the critical components to consider in the assessment.They are afterwards modelled as simplified geometries within the subsequent platform modelling phase.The shotline scanning method phase represents the heart of the whole vulnerability framework,which by means of ray tracing algorithms allows determining the components impacted by the threat.This information is then post-processed exploiting penetration algorithms,which are implemented in the proposed framework according to an innovative solution in the survivability field,allowing the characterization of the threat state-of-motion while passing through the components along its trajectory.Finally,the last phase of the vulnerability assessment includes a vulnerability statistical framework,which outputs the kill probability of the components,of the systems,of the group of redundant components and of the whole platform.

Fig.15.Overlap area of the dummy components in two relevant aspects.
In particular,since no exhaustive modern application of such an approach on helicopters is present in the literature yet,a detailed analysis of a vulnerability assessment focused on helicopters threatened by projectiles has been reported herein and for this purpose a helicopter platform under the threat of a 7.62 x 54 API B-32 projectile(limited to the penetration capability)has been analyzed.Each of the five previously identified phases has been discussed with a focus on the case study,from the identification of the critical components up to the penetration assessment of the projectiles under investigation.Finally,the statistical results have been provided in form of 3D bars,for the Pvalue of the global helicopter,and 2D curve plots,which identify the killability of the platform and of each of its systems.
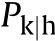
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
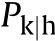
The presented area of the i-th component is computed as:

where Nis the number of shotlines impacting the i-th component,while sis the area of each square cell of the shotlines grid,being s the linear dimension of each cell in Fig.4(b).The presented area identifies the i-th component projection on the considered aspect.
The single-component vulnerable area directly follows from the definition of its presented area,according to the following Eq[1].:

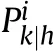
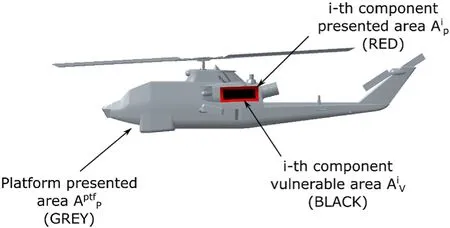
Fig.16.Presented and vulnerable areas.
The component killability is then computed as[1]:

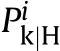
The kill probability of a group of redundant components is determined by means of the following original procedure,which is based on the Ball's theory[1].The j-th group vulnerability value given a hit on the group itself,i.e.,provided that all of its components are hit,is computed as:

where Grepresents the set of redundant components which are part of the j-th group.A hit flag is computed for each group,considering each shotline,as:

which identifies if the j-th group is hit along the n-th shotline.In that equation,hitis a Boolean operator holding TRUE if and only if the i-th component is stored in the n-th final shotline hit sequence.Hence,the value of the presented area of the j-th group in the current aspect becomes:

where Ais the presented area of the n-th shotline,i.e.,the grid cell area s.The vulnerable area and killability of the group then read:

The killability of a system is computed by means of an original procedure based on the Ball's theory[1],which allows considering the system vulnerability value variability with respect to the shotline considered.The vulnerability of the k-th system along the n-th shotline is given by:

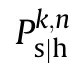

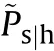
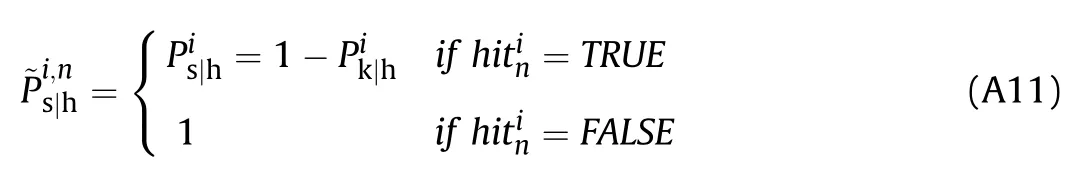
and similarly for the j-th group.Hence,the presented and vulnerable areas of the system in the current aspect become:
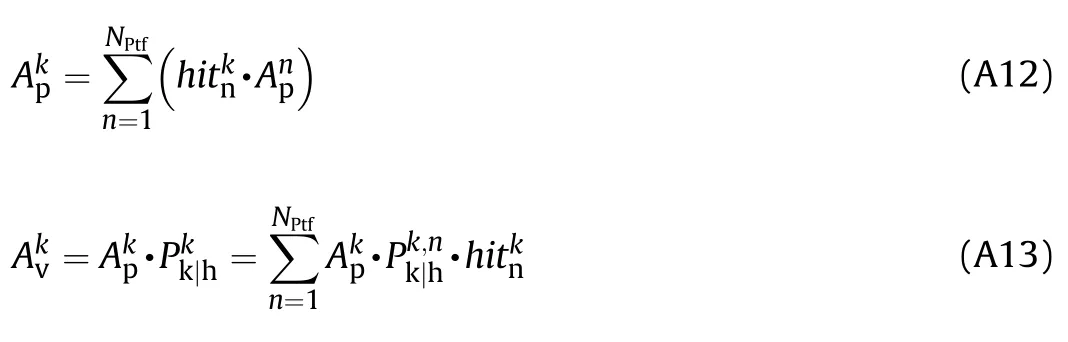
where hitrepresents the hit flag of the k-th system,which holds TRUE if at least one non-redundant critical component or group of redundant components in the system is hit by the n-th shotline.Finally,the k-th system killability in the current aspect is computed as:

The platform killability is computed through the vulnerability of each shotline not discarded by the ray tracing and penetration algorithms,i.e.,those for which a final shotline hit sequence is provided[1].The n-th shotline vulnerability is computed as:

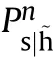
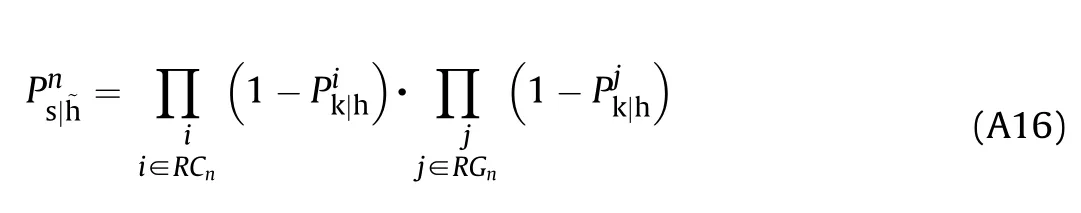
where RCand RGare the sets of non-redundant components and groups of redundant components hit by the n-th shotline,respectively.Hence,the vulnerable area of the n-th shotline directly follows:

Finally,the platform killability is computed as:

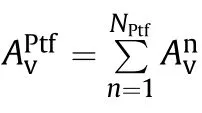
杂志排行
Defence Technology的其它文章
- 3D laser scanning strategy based on cascaded deep neural network
- Damage analysis of POZD coated square reinforced concrete slab under contact blast
- Autonomous maneuver decision-making for a UCAV in short-range aerial combat based on an MS-DDQN algorithm
- The properties of Sn—Zn—Al—La fusible alloy for mitigation devices of solid propellant rocket motors
- The surface activation of boron to improve ignition and combustion characteristic
- Numerical investigation on free air blast loads generated from centerinitiated cylindrical charges with varied aspect ratio in arbitrary orientation
