双边定数截尾下Pareto分布的Bayes估计

刘 芹，周菊玲

(新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017)

0 引言

在可靠性分析与寿命分析等领域中，常会出现数据缺失的情形，而双边定数截尾数据是一种特殊的缺失数据，其模型为：在可靠性实验中假定选取n个产品投入实验，直到r个产品失效时终止实验，设观察到的次序失效数据为x1≤x2≤…≤xr。在实际问题中，由于实验手段等其他因素的影响，导致有些数据未被观察到。假设前s-1个数据丢失，则剩下的次序数据xs≤xs+1≤…≤xr，1≤s≤r≤n，此数据即为双边定数截尾样本。对于此类样本，有不少学者对其展开了研究，李艳玲[1]研究了双参数指数分布在双边定数截尾下的贝叶斯预测问题，郭红莹等[2]、邓严林[3]在双边定数截尾下分别研究了Burr分布、Topp-Leone分布参数的Bayes估计，田霆[4]在双边定数截尾下讨论了Weibull分布两参数的联合置信区间。

Pareto分布是一种重要的寿命分布，具有递减的失效函数，因此常被应用于个人收入、股票价格的波动、保险风险等模型。该分布的概率密度函数及分布函数为：

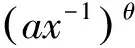
(1)

式中：a>0，θ>0，a为尺度参数，θ为形状参数。近年来关于Pareto分布的研究有很多，例如，李如兵等[5]在移动极值排序集抽样下，针对共轭先验和杰弗莱先验，研究了Pareto分布形状参数的Bayes估计；周巧娟等[6]基于定数截尾数据，在复合Mlinex损失下，研究了Pareto分布参数的稳健Bayes估计；刘璐等[7]在定数截尾试验时，给出了Pareto分布参数的最优置信区间，使得估计更加精确；Han等[8]在不同损失函数下研究了Pareto分布形状参数的E-Bayes估计及其均方误差。本文在前面学者研究的基础上，基于双边定数截尾样本研究Pareto分布在LINEX损失函数和复合LINEX函数下参数的Bayes估计问题。

1 预备知识

在Bayes统计决策中，无信息先验分布和共轭先验分布是两种常用的先验分布，Pareto分布参数的这两类先验分布有如下形式：

(2)

(3)

对于双边定数截尾样本，当产品服从Pareto分布时，记x=(xs，xs+1，…，xr)，则由文献[2]知样本(xs，xs+1，…，xr)的联合分布密度函数为：

(4)

将(1)式带入式(4)得到

(5)

2 参数的Bayes估计

2.1 LINEX损失函数下参数的Bayes估计

取LINEX损失函数

Lc(θ，δ)=ec(θ-δ)-c(θ-δ)-1，c≠0

(6)

这里讨论c>0的情况。

引理1 在LINEX损失函数下，对于任意先验分布π(θ)，θ的Bayes估计为

(7)

且若此估计的Bayes风险有限，则它是唯一的Bayes估计。

定理1 设X=(X1，X2，…,Xn)是服从Pareto分布的简单随机样本，在LINEX损失函数下，有以下两种情况

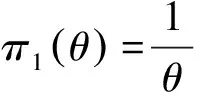
(8)

(9)

证(i)由(2)和(5)式，根据Bayes公式可得θ在无信息先验分布下的后验分布

(10)

式(10)的分母可化为

由引理1可知，在无信息先验分布下参数的Bayes估计为

(ii)由(3)和(5)式，根据Bayes公式可得参数θ在共轭先验分布下的后验分布为

(11)

由引理1可知在共轭先验分布下参数的Bayes估计为

2.2 复合LINEX损失函数下参数的Bayes估计

复合LINEX损失函数的表达式为

L(θ，δ)=L-c(θ，δ)+Lc(θ，δ)=e-c(θ-δ)+ec(θ-δ)-2，c>0

引理2 在复合LINEX损失函数下，对任意先验分布π(θ)，θ的Bayes估计为

(12)

定理2 设X=(X1，X2，…,Xn)是服从Pareto分布的简单随机样本，在复合LINEX损失函数下，有以下两种情况

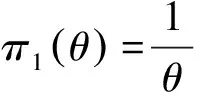
(13)

(14)

由引理2，类似定理1 的证明过程即可证得。

3 数值模拟

表1 模拟结果

由表1可知，在同一个损失函数下，对比两先验先分布下参数估计的均方误差，发现共轭先验分布下参数估计的均方误差较小，因此参数θ取共轭先验分布时，参数的Bayes估计更接近真值；在同一个先验分布下，LINEX损失函数下参数的Bayes估计的均方误差较小，同时在LINEX损失下，参数θ取共轭先验分布时，参数的Bayes估计模拟效果更好。

4 实例分析

Arnold在其著作中给出了一组服从Pareto分布的数据。 50名高尔夫球手收入超过70 000美元，他们到1980年为止的收入为3581、1690、1433、1184、1066、1005、883、841、778、753、2474、1684、1410、1171、1056、1001、878、825、778、746、2202、1627、1374、1109、1051、965、871、820、771、729、1858、1537、1338、1095、1031、944、849、816、769、712、1829、1519、1208、1092、1016、912、844、814、759、708美元，且这些数据服从尺度参数a≈703，形状参数θ≈2.23的Pareto分布。

首先将上述数据按照由小到大的顺序排列，然后利用R软件根据这组数据选取其中符合要求的部分进行参数估计。这里仅考虑在不同损失函数下先验分布选Γ分布的参数估计，设c=10，α=100，β=100。结果如表2所示。

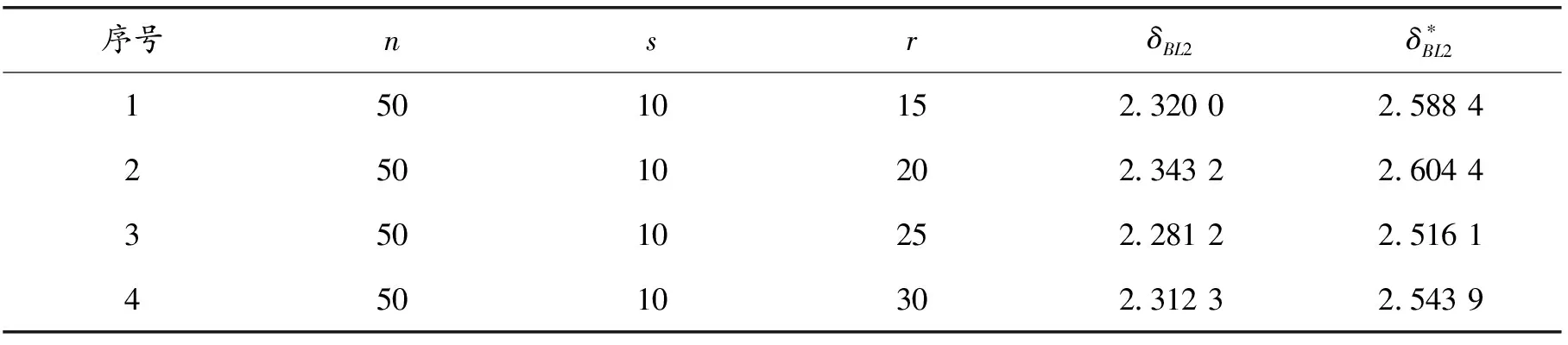
表2 形状参数的Bayes估计

由表2可知，当样本量一定并且先验分布选Γ分布时，参数在LINEX损失下估计的偏差最小，此时的参数估计效果较好，且与数值模拟的结果一致。

5 结论

双边定数截尾是一种在可靠性试验中会遇到的特殊截尾数据。本文在双边定数截尾场合下，基于LINEX损失函数和复合LINEX损失函数，采用Bayes估计的方法对Pareto分布中的形状参数进行估计。在无信息先验分布和Γ先验分布下，将不同损失函数下参数的Bayes估计与其真值进行比较分析，结果表明，在LINEX损失下，选用Γ先验分布时，参数估计更接近真值，并且通过实例也验证了此结论。