小波包软阈值降噪法在航空γ能谱中的应用

张 松胡传皓李承洋王 楠严 磊李雪刚曾国强顾 民

（成都理工大学 成都 610059）

因航空γ能谱测量方法具有探测速度快、便于大面积测量等优势，已经成为放射性物质勘探的主要方法之一［1-2］，并被广泛地应用于地质填图、金属矿产勘查、辐射环境评价等众多领域［3-4］。深部放射性矿体、非放射性矿体以及地表和浅层隐伏矿体等的放射性非常微弱，分布形态也很复杂，这对航空γ能谱测量系统的灵敏度和测量精度提出了更高的要求［5-6］。一套高分辨率航空γ探测系统的研发时间长、难度大，因此，对现有的航空γ探测系统测量得到的γ能谱进行降噪是一种快速提高测量精度的方法。

在降噪领域，小波分析是泛函分析、Fourier分析、样条分析、调和分析的最完美结晶［7］。它可以追溯到1910年Haar提出的小“波”规范正交基及1938年Littlewood-Paley对Fourie级数建立的L-P理论［8-9］。之后，在1987年，Mallat［10］将多尺度分析思想引入到小波分析中，并提出Mallat算法对信号进行分解与重构。再到1991年，Wickerhanser等［11］对Mallat算法进一步深化，得到了小波包算法。现在，小波包变换理论非常丰富，在时域和频域都具有良好的局部化性质，可以将频带进行多层次划分，极大地提高了时-频分辨率，能够准确地降低信号的噪声［12］。航空γ能谱测量具有计数率低、测量速度快的特点，导致航空γ能谱的信噪比较低，因此，对航空γ能谱进行降噪很有必要［13］。本文将采用小波包软阈值降噪法对航空γ能谱仪中47个CeBr3探测器测得的能谱进行降噪处理，并对小波分解的层数和不同母小波两个方面进行分析，通过比较不同方案降噪后的峰值信噪比，以及降噪对准确度的提升效果，寻找到一种最适用于航空γ能谱的小波包软阈值降噪方案。

1 小波包变换原理

小波包函数［14-15］既有尺度指标j和位置指标k，又有频率指标n，其表达式为：

式中：φnj(t)是小波包空间中分解的子小波，其表达式为：

式中：W j，nl表示第-j层分解后的小波子空间，j=…，-1，0。其小波包分解算法可以由｛W j+1，nl｝的递推性质求出｛W j，2nl｝与｛W j，2n+1l｝：

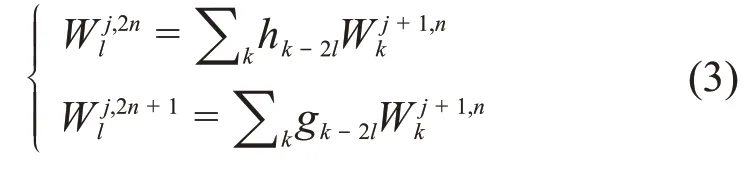
式中：hk-2l为低通滤波器；gk-2l为高通滤波器，最后由小波包的双尺度方程：

可得到由｛W j，2nl｝与｛W j，2n+1l｝重构出｛W j+1，nl｝的小波包重构算法：

2 小波包软阈值降噪方法的实现

下面介绍小波包软阈值降噪法的实现。该方法主要分为4个步骤：1）选择一种母小波，确定分解的层次，然后对信号进行小波包分解；2）根据熵标准求出最优分解树，得到最优小波包基；3）选择一种合适的软阈值边界，对于每一个小波包分解的系数，进行阈值量化处理；4）对低频系数和软阈值量化处理后的高频系数进行小波包重构，得到降噪后的信号。

2.1 母小波的选择与最优小波基的计算

第一步：母小波的选择需要使用各种小波和各种分解层数进行降噪处理，根据最终的降噪效果进行确定；第二步：对信号进行小波包分解，图1为小波包二层分解的分解树示意图。

如图1所示，每层小波分解将信号S分成了低频成分A和高频成分D，如AD2（L/2）依次表示该层为低频成分A，上层为高频成分D，该层为第二层，频带宽度为L/4。当某个节点继续分解下去无法有效区分信号的真实成分和噪声成分，便无需继续进行分解。可以通过熵标准求得最佳分解树，本文采用Shannon熵作为熵标准，Shannon熵可由式（6）求得：

图1 小波包分解树Fig.1 Wavelet decomposition tree

式中：si，j表示分解树中第i层第j个节点的分解系数；E(Si，j)是该节点的熵值，其值越大，表示离散程度越低，其离散势能越大。真实成分的离散程度比噪声成分的离散程度高，因此，低频成分的熵值会小于高频成分的熵值，当某个节点分解后，低频成分的熵值与高频成分的熵值差距很小，或者低频成分的熵值大于高频成分的熵值时，就表明该节点无需再分解。通过计算并比较每个节点的熵值大小，就可以得到最佳分解树［16］。

2.2 基于极大极小(minimaxi)规则确定边界的软阈值函数

对于小波包软阈值降噪法，第三步选择合适的软阈值非常重要。本文根据航空γ能谱信噪比较低的特点，将软阈值函数与硬阈值选取方法相结合，利用硬阈值选取方法中比较保守的minimaxi规则确定的硬阈值作为软阈值函数的边界。软阈值法可以提高降噪效果，minimaxi规则确定的软阈值边界可以减少信号的失真［17-18］。软阈值函数可表示为：

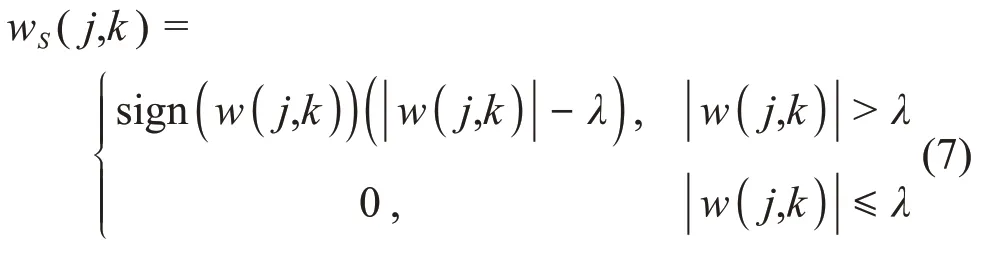
式中：λ为软阈值的边界；minimaxi规则确定的硬阈值为：

式（8）是针对标准差为1的高斯白噪声而言，实际上minimaxi阈值应为Tr∙σ。

式中：Mx表示含噪信号最小尺度上的小波系数绝对值向量的中位数，因此软阈值的边界为：

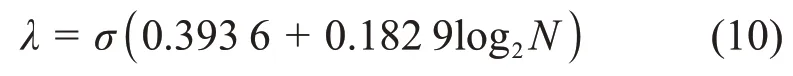
将一个呈线性正增长的系数经过该软阈值进行处理后，效果如图2所示。点划线线表示原始小波分解的系数，虚线表示经过边界为λ的软阈值进行处理后的系数。第四步将阈值处理过的节点系数进行小波包重建即可得到降噪信号。

图2 软阈值处理效果Fig.2 Soft threshold processing effect

2.3 降噪效果的评价方法

本文使用拟合的方法将原始谱中137Cs峰附近与40K峰附近的谱线进行拟合，并将拟合谱线作为原始谱线真实成分的估计值，再计算并使用平均峰值信噪比（Average Peak Signal-to-noise Ratio，APSNR）作为降噪效果的评价标准［19-20］。

航空γ能谱中的全能峰是净全能峰和康普顿平台的叠加，净全能峰服从高斯分布，康普顿平台在全能峰区域可以近似为反正切函数曲线，因此，拟合采用的特征函数是一个高斯函数加一个反正切函数，其表达式为：

使用该方法对测量30 min的γ能谱中137Cs峰附近的高计数谱线进行拟合，效果如图3所示。对测量1 min的γ能谱中40K峰附近的低计数谱线进行拟合，效果如图4所示。

图3 测量30 min能谱中137Cs峰附近谱线的拟合效果Fig.3 Fitting effect of the spectral lines near the137Cs peak in the 30-min measured energy spectrum

如图3所示，反正切函数拟合部分很好地反映了康普顿平台，137Cs峰附近高计数谱线在含有噪声的情况下，拟合度达到了99.996%。因此，可以判断该拟合方法能够非常准确地拟合出谱线的真实成分。如图4所示，拟合谱线始终在原始谱线的中间，40K峰附近谱线的拟合度为92.91%。因此，可以将拟合谱线视为原始谱线的真实成分。峰值信噪比的计算如下：

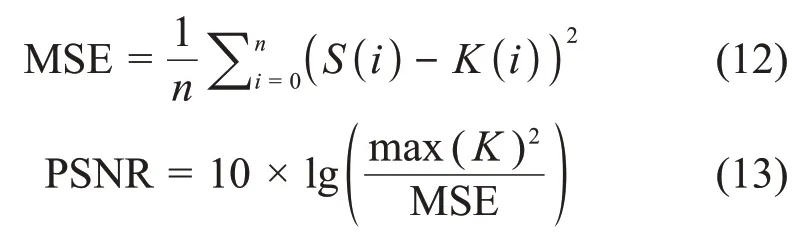
式中：S(i)表示降噪后的谱线；K(i)表示原始谱的拟合谱线。PSNR的值越大，降噪效果越好。为了消除采样周期和不同峰位的影响，本文将计算n种采样周期下的40K峰附近谱线的和208Tl峰附近谱线的，然后计算出第i种采样周期Ti下的PSNRTi：

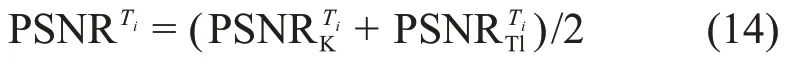
最后求出平均峰值信噪比APSNR：

通过计算降噪后谱线的APSNR可以综合性地评价不同小波基和不同分解层数下的小波包软阈值降噪法的降噪效果，并最终选择出最优母小波及其对应的分解层数。

3 最优小波包软阈值降噪方案的选择和应用

下面使用不同母小波和不同分解层数的小波包软阈值降噪法对航空γ能谱进行降噪，分析出最优的母小波和对应的分解层数，并应用在准确度测量中。母小波选用MATLAB软件中包含的56种小波，其中包括db系列小波、sym系列小波、coif系列小波、rbio系列小波、fk系列小波、haar小波和demy小波，分解层数选用1~15层进行研究。在航空γ能谱测量中，采样周期为1~5 s，每次采样的能谱计数非常低。因此，本文将对一段时间内所采集的所有能谱数据依次进行降噪，并分别将这一段时间内的所有原始谱线、降噪后谱线进行合成，然后对合成后的谱线进行分析。

3.1 小波包分解层数对信号失真的影响

分解层数越多，越能够将信号的细节成分进行区分，但每次重构都会造成失真，因此需要研究分解层数对信号失真的影响。下面使用sym6小波依次进行1~15层分解，对采样周期为1 s、共测量1 min、5 min、10 min、15 min的信号分别进行降噪处理。

失真情况使用原始谱线和降噪后谱线的40K全能峰峰区总计数进行比较，如图4所示，将道址区间为［7 860:7 950］的谱线进行累加即可得到40K全能峰的峰区总计数，再将降噪后的峰区总计数除以原始谱线的峰区总计数，然后乘以100%，就可以消除时间量纲，得到降噪后的峰区总计数占原始谱线的峰区总计数的百分比，结果如图5所示。

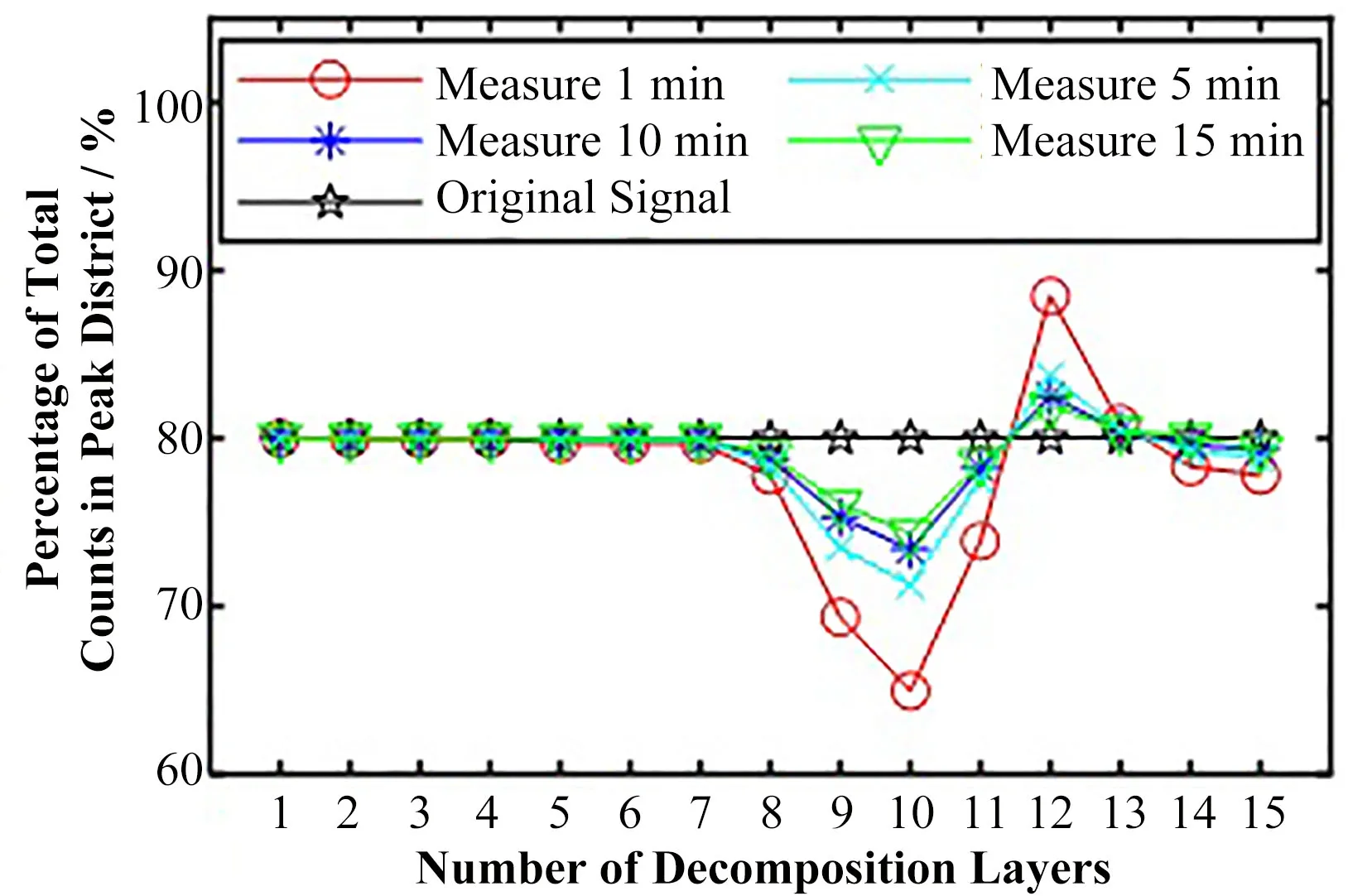
图5 不同测量时间与分解层数对信号失真的影响Fig.5 Influence of different measurement time and decomposition layers on signal distortion

由图5可知，当分解层数为1~7层时，降噪所产生的失真幅度都小于0.5%，而当分解层数增大到8层之后，失真就非常明显。这是因为小波分解层数越多，重构的次数也越多，不断重构会使失真逐渐积累，最后造成严重的失真。另外，分解层数越多运算所需的时间也越长，因此在使用小波包软阈值降噪法时，分解层数不应该大于7层。

3.2 最优母小波与分解层数的选择

为了综合性地评价不同母小波及不同分解层数的小波包软阈值降噪法的降噪效果，下面将56种母小波分别进行1~7层分解，并分别对测量总时长为1 min、采样周期分别为1 s、2 s、3 s、4 s、5 s的航空γ能谱进行降噪。首先，使用一种母小波对一种谱线进行降噪，并求出不同分解层数下的PSNR，并选出该条件下该母小波的最佳分解层数，再将最优的PSNR作为该母小波在该条件下的或。最后根据不同条件下的和求出PSNRTi和APSNR。各母小波的最优分解层数选用该母小波在不同条件下最佳分解层数的众数。经计算，原始谱线的APSNR为23.22 dB，由各种母小波进行最优分解的小波包软阈值降噪法的降噪效果如表1所示。

由表1可知，降噪效果最好的是db14母小波，最优分解层数为7层，其降噪后的平均峰值信噪比为39.50 dB，比原始谱线的平均峰值信噪比的23.22 dB提升了16.28 dB。由于本文是将拟合估计出的谱线作为真实谱线，与真实情况会有一点误差，因此将排在前5的母小波应用在航空γ能谱仪的准确度测量中，进一步进行分析。

表1 56种母小波的最优分解层数和平均峰值信噪比Table 1 Optimal number of layers and average peak signal-to-noise ratio for 56 mother wavelets

3.3 小波包软阈值降噪法对准确度的提升效果

下面分别使用前5种降噪方案对航空γ能谱仪在地面模型中测得的数据进行降噪处理，并计算出对应的准确度，结果如表2所示。

表2 5种降噪方案对准确度的提升效果Table 2 The effect of five noise reduction schemes on accuracy improvement

如表2所示，5种降噪方案都能够提升航空γ能谱仪的准确度，其中由db14小波进行7层分解得到的小波包软阈值降噪法对准确度的提升效果最好，将总误差减少了3.19%。因此，本文将由db14小波进行7层分解得到的小波包软阈值降噪法视为最优降噪方案。

3.4 最优小波包软阈值降噪方案的降噪效果

下面使用db14母小波进行7层分解的小波包软阈值降噪法对测量时间为1 min、采样周期为1 s的航空γ能谱依次进行降噪与合成，效果如图6、7所示。

如图6、7所示，使用最优母小波db14进行7层分解的小波包软阈值降噪法降噪后，谱线更加平滑，且看不出失真。图6中降噪后的PSNR为39.22 dB，相比原始谱线的21.52 dB提升了17.7 dB；图7中降噪后的PSNR为39.78 dB，相比原始谱线的23.40 dB提升了16.38 dB。另外，对测量时长为1 min、采样周期分别为1 s、2 s、3 s、4 s、5 s的信号使用db14母小波进行降噪后，PSNR分别为39.78 dB、39.74 dB、39.66 dB、39.62 dB、39.56 dB，呈下降趋势，使用其他母小波降噪也有此现象。可见，使用小波包软阈值降噪法对信噪比越低、采样周期越短的谱线进行降噪后，峰值信噪比的提升效果越明显。

图6 1 min40K峰的降噪效果Fig.6 Noise reduction effect of 1 min measured40K peak

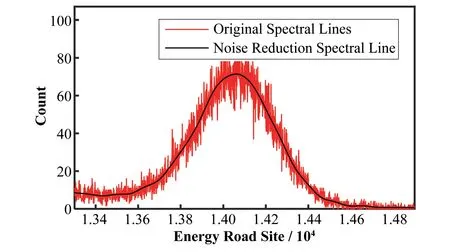
图7 1 min208Tl峰的降噪效果Fig.7 Noise reduction effect of 1 min measured208Tl peak

4 结语

本文介绍了小波包软阈值降噪法的基本原理，分析了不同分解层数对降噪效果的影响，通过比较不同降噪方案的平均峰值信噪比，选出了5种降噪方案应用在准确度测量中，还通过比较这5种降噪方案对准确度的提升效果，选出了最优的降噪方案。结果发现：小波分解层数只要不超过7层，就不会产生明显的失真；排名前三的降噪方案是选用db14母小波、dmey母小波和rbio6.8母小波进行7层分解的小波包软阈值降噪法；将排名前5的降噪方案应用在准确度计算中发现，5种降噪方案都能够提升航空γ能谱仪的准确度，其中最优的是使用db14母小波进行7层分解的小波包软阈值降噪法，该方案将谱线的峰值信噪比从23.22 dB提升到了39.50 dB，且将测量的准确度提高了3.19%。可见，小波包软阈值降噪法的降噪效果好、造成的信号失真少，适合应用于航空γ能谱的数据处理中。

作者贡献声明张松：直接参与论文研究，负责实验与模拟，负责小波包软阈值降噪模型搭建并撰写论文；胡传皓：指导实验操作和论文修改；李承洋：辅助测量；王楠：辅助测量；严磊：指导程序设计；李雪刚：辅助测量；曾国强：指导论文修改，提供技术支持；顾民：指导论文修改，提供技术支持。