核孔膜表面重孔分布的研究
2022-09-21傅楗强
傅楗强
(清华海峡研究院(厦门)厦门 361015)
利用核反应堆或加速器产生的重离子辐照固体膜材,在膜材上造成辐射损伤形成潜径迹,后经化学蚀刻,损伤区域可形成纳米至微米级的穿透性通道[1‒2]。用该方法制成的核孔膜具有表面坚实光滑、孔径均一、截留率高等特性,已应用于医药精密过滤、生化分析、电池隔膜、微量探测等诸多高端领域[3‒6]。
核孔膜的孔隙率及重孔分布直接影响了核孔膜过滤器的滤除率和渗透性[7‒8]。当孔隙率很小时,孔分布基本为单孔,此时核孔膜对大于蚀刻孔径的固体微粒的滤除率接近100%,但渗透性较差。增大孔密度可以增加孔隙率,使核孔膜渗透性增强,但孔发生重叠的概率增大,重孔现象严重影响了孔的平均孔径,使得核孔膜对接近蚀刻孔径的固体微粒的滤除率大大降低。核孔膜的许多应用中,对滤除率和渗透性的性能指标有着严苛的要求,而这两个参数通常是负相关的。因此,考察核孔膜孔隙率与重孔分布情况显得尤为重要。
本文基于蒙特卡罗模拟方法开发模拟分析程序,模拟计算特定辐照注量、蚀刻条件下的孔隙率与重孔分布之间的关系,并将计算结果与理论推导、扫描电子显微镜观测结果进行比照。重孔率的模拟计算结果与理论公式推导结果符合,重孔分布情况与扫描电子显微镜观测结果吻合,验证了模拟分析程序的准确性。
本研究工作对核孔膜的定制化生产具有实用意义,可作为核孔膜生产中优化辐照注量和蚀刻孔径大小等工艺参数的辅助工具,以满足特定核孔膜过滤器的最佳参数配置。
1 模拟计算方法
1.1 蒙特卡罗方法
蒙特卡罗方法是核物理模拟中常用的方法[9]。蒙特卡罗方法的基本思想是:建立一个概率模型或随机过程,使它的参数或数字特征等于问题的解;通过对该模型或过程的抽样试验来计算这些参数或数字特征;最后给出所求解的近似值。
本文基于蒙特卡罗思想,模拟加速器重离子入射固体膜材,后经化学蚀刻形成孔道的过程[10],并对核孔膜表面孔道进行统计分析,从而得出孔隙率、重孔分布情况等数据。
随机数生成是蒙特卡罗模拟的基础,本文中伪随机数的产生及后续的统计分析均通过ROOT编程实现。ROOT是CERN开发的针对高能物理数据处理的面向对象的软件框架[11],主要用于粒子物理实验的数据分析和统计,具有强大的作图功能,已被广泛应用在高能物理、核物理等领域中。
1.2 分析程序简介
基于ROOT编写了核孔膜表面重孔分布分析程序。该程序开发了可视化界面,操作简单,可快速计算出结果。程序界面如图1所示,在工艺参数设置栏,可对孔密度、蚀刻孔径进行设置。在分析绘制栏,可模拟化学蚀刻,利用ROOT的作图功能,绘制核孔膜表面蚀刻微孔的分布;可计算孔隙率和重孔分布情况,并输出计算结果到txt文档中。目前的程序版本中,重离子垂直入射固体膜材,对化学蚀刻采用了最简单的圆柱形孔道蚀刻模型。
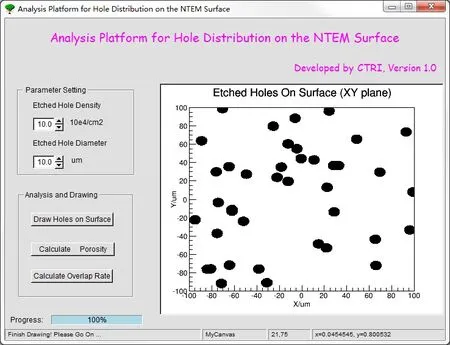
图1 核孔膜表面重孔分布分析程序平台Fig.1 Analysis platform for hole distribution on the NTEM surface
1.3 计算方法
1.3.1 表面蚀刻微孔的绘制
假设入射重离子在空间的分布满足二维的均匀分布。算法步骤如下:
1)利用ROOT中的gRandom生成器随机生成N0个 服 从 均 匀 分 布 的 二 维 坐 标(xi,yi),i=1,2,3,…,N0。其中:N0=n⋅S,n为孔密度,S为模拟计算采用的核孔膜面积,S默认为1 mm2的正方形。
2)利用ROOT中的TH2F类新建像素数目为k×k的二维图像,图像对应的面积为S。为了保证计算精度,每个像素尺寸设为孔径D的1/1 000,即k=
3)遍历坐标数组(xi,yi),将(xi,yi)以为圆心,D为直径区域内的像素值置为1。
4)绘制黑白二值图像,即为核孔膜表面蚀刻微孔的分布图。图1绘制的图像,为了显示效果,已将显示区域调整为孔径的20倍。
1.3.2 孔隙率的计算
若忽略重孔,孔的总面积可认为是所有单孔简单的线性叠加,本文定义标称孔隙率为η,假设孔密度为n,孔呈圆形、且孔径为D,则:

实际的核孔膜中,由于孔之间存在重叠现象,实际孔隙率ηeff<η(下文将实际孔隙率简称为孔隙率)。
孔隙率的计算基于§1.3.1的k×k二维图像的结果。对二值图像而言,用1表示孔道,用0表示膜材,孔的总面积就是统计图像内灰度值为1的像素数量。对k×k的二维矩阵进行求和,得到孔的像素总数,再除以图像总像素数k2,即可得到孔隙率ηeff。
1.3.3 重孔分布的统计
核孔膜表面的孔可分为单孔、双重孔、三重孔、直至m重孔。计算重孔分布的算法步骤如下:
1)利用ROOT中的gRandom生成器随机生成N0个 服 从 均 匀 分 布 的 二 维 坐 标(xi,yi),i=1,2,3,…,N0,其中:N0=n⋅S。
2)对于每个二维坐标(xi,yi),对应一个mi用于标记该孔为m重孔,mi初始值为1。
3)通过循环函数遍历i从1至N0,对每一个孔的圆心(xi,yi),计算(xi,yi)与之前的所有孔的圆心(xj,yj),j 4)对重孔分布进行统计,通过mi值判断该孔属于单孔、双重孔、三重孔或是m重孔,得出重孔概率分布情况(单孔概率P1,双重孔概率P2,三重孔概率P3,m重孔概率Pm)。 5)对双重孔、三重孔或是m重孔,分别计算每个重孔的有效孔道面积(即统计该重孔区域内灰度值为1的像素的数量),进而统计得出重孔面积分布的概率密度函数。 2.1.1 重孔率的理论推导 本文定义重孔率为: 式中:Noverlap和Ntotal分别是核孔膜表面重孔的孔数和孔的总数。重孔率的理论推导如下: 根据碎片入射分布的统计独立性,在面积F上发现k个孔的概率服从泊松分布[12]: 式中:n为孔密度;nF为分布在面积F上的孔平均数目。重孔率的表达式可由式(3)推导得出。假设直径为D的孔H0位于坐标原点,孔H1是与孔H0相邻最近的孔,孔H1与原点距离为r。如图2所示,孔H1出现在r处的概率为: 图2 重孔概率的计算示意图Fig.2 Schematic diagram of calculation for overlap probability 若孔H1与孔H0发生重叠,则孔H1必然位于以原点为圆心,以D为半径的圆形范围内,现在计算这一概率。对式(4)进行积分,得到重孔率的表达式为: 参考式(1),可见重孔率与标称孔隙率η存在简单的函数关系[13]。 2.1.2 重孔率的模拟计算 利用模拟分析程序,计算不同孔径D下,重孔率Woverlap=Pm>1随孔密度n的变化趋势。如图3所示,实点为模拟计算结果,实线为根据式(5)绘制的理论曲线。可见模拟计算结果与理论曲线相吻合,证明了模拟分析程序在重孔率计算上的准确性。 根据式(5),重孔率与标称孔隙率η之间存在的函数关系,该函数关系不受孔密度n和孔径D影响。 下面探讨重孔率与实际孔隙率ηeff之间的关系。对图3的数据实点,分别计算各数据点对应的孔隙率ηeff。以孔隙率ηeff为横坐标,重孔率为纵坐标,绘制散点图如图4所示。从图4中可见,不同孔密度n、孔径D下,散点分布也满足一定趋势,即重孔率与实际孔隙率ηeff也满足一定的函数关系。 图3 不同孔径下,重孔率随孔密度的变化曲线Fig.3 The curve of overlap rate with hole density under different hole diameters 图4 重孔率随孔隙率的变化曲线Fig.4 The curve of overlap rate with porosity 对图4的散点进行拟合,拟合函数关系为: 从式(6)可知,重孔率和孔隙率这两个产品参数呈正相关关系,在生产中不能独立控制。当孔隙率为10%时,此时的重孔率已接近35%;当孔隙率为30%时,重孔率接近80%。在核孔膜的许多应用中,都需考量重孔的影响。 2.2.1 重孔分布的模拟计算 随着孔隙率的增加,重孔现象越发显著。下面对单孔概率P1,双重孔概率P2,三重孔概率P3,m重孔概率Pm进行分析计算。由于重孔形态的分布比较复杂,数学上难以用较为简单的公式来描述Pm。通过模拟分析程序计算不同孔隙率下,Pm随孔隙率ηeff的变化曲线,如图5所示。单孔出现的概率P1单调递减,而重孔出现的概率不断增加;多重孔出现概率Pm的峰值随着重孔数目m的增加而右移。 图5 多重孔分布概率随孔隙率的变化曲线Fig.5 Variation curve of the probability of multiple hole overlap with porosity 下面对每个重孔的面积开展统计分析。 双重孔的形态分布最为简单,若孔H1与孔H0相重叠,则孔H1和孔H0两者圆心的距离r必定小于D。参考图2,r的分布满足如下概率密度函数: 当r=0时,孔H1与孔H0完全重叠,此时双重孔面积最小,为πD2/4。随着r的增大,该种形态的双重孔出现的概率也增大,且对应的双重孔面积也增大。当r接近D时,孔H1与孔H0略微重叠,此时双重孔面积最大,接近πD2/2。三重以上的重孔,形态分布较为复杂,难以用解析方法描述。利用模拟计算程序对重孔的面积分布情况进行统计,分别得到双重孔、三重孔、m重孔的孔面积分布的概率密度函数PS,2、PS,3、PS,m。 计算结果表明,不同的孔密度n和孔径D下,重孔重叠的形态分布是相似的,PS,m概率密度分布函数也是相似的。图6的统计中,已将重孔的孔面积除以单孔的面积,对横坐标进行归一化。从图6中可见,对于m重孔,孔面积分布从1到m。双重孔面积分布从1到2,面积接近2时几率最大。随着重孔数m的增加,重孔分布的形态越发复杂,孔面积分布也较为分散。对于三重孔,孔面积分布函数PS,3的极大值对应横坐标为2.85。对于四重孔、五重孔,PS,3、PS,4的极大值对应横坐标分别为3.25和4.10。 不同孔隙率下,核孔膜表面孔的面积分布概率函数PS,total,可通过§1.3.3的算法用蒙特卡罗方法模拟计算得出。基于图5和图6的结论,可推导出PS,total的代数解析表达式(8),即对m重孔的出现概率Pm和面积分布概率密度函数PS,m的进行加权求和。利用该解析表达式可快速计算PS,total。 图6 多重孔面积的概率密度分布函数Fig.6 The probability density function(PDF)of the area of multiple hole overlap 核孔膜的应用中,经常同时要求高渗透性和高滤除率。高渗透性意味着高孔隙率,而高孔隙率下不可避免地出现高重孔率。重孔导致核孔膜实际滤除粒径大于蚀刻孔径D,因此需要减小蚀刻孔径D来保证滤除率。在蚀刻孔径D较小的情况下保持高孔隙率,需要增大孔密度n。综上所述,高孔密度且小蚀刻孔径的核孔膜可同时满足高渗透性和高滤除率要求。而核孔膜生产中,加速器束流是主要的成本,高孔密度意味着辐照时长变长,成本增加;另一方面,蚀刻过程中对数十nm以下的孔径需要更为复杂的工艺。 利用该模拟分析程序,在满足核孔膜性能指标的情况下,优化生产中辐照注量和蚀刻孔径等工艺参数,尽量节约生产成本和简化生产工艺。 2.2.2 重孔分布的实验结果 为了验证模拟程序的可靠性,对两种核孔膜样本采用扫描电子显微镜(Scanning Electron Microscope,SEM)进行观测[14]。利用电子显微镜照片,统计得到视野范围内孔密度和孔径大小,并对重孔分布情况进行统计。 根据观测的孔密度和孔径大小,利用模拟分析程序绘制相同参数下的孔分布图片,并计算其相应的重孔分布情况。 图7展示了核孔膜的电子显微镜照片和模拟分析程序绘制的图片,图中核孔膜的孔密度和孔径等参数详见表1。对比模拟分析性程序绘制的图片和电子显微镜的观测照片,可见两者的孔分布在宏观上对照得很好。 图7 核孔膜的电子显微镜照片(a、b)和模拟分析程序绘制的表面孔分布(c、d)Fig.7 SEM images of nuclear track-etched membranes(a,b)and pictures of hole distribution draw by the analysis platform(c,d) 表1 核孔膜样本观测的多重孔概率和模拟结果的对比Table 1 The comparison of the probability of multiple hole overlap between experimental observation and simulation 对扫描电子显微镜下多个视野中的核孔膜照片开展重孔统计分析,得到单孔概率P1,双重孔概率P2,m重孔概率Pm。表1对比了核孔膜样本的重孔分布观测结果和模拟分析程序计算结果。 理论上核孔膜表面的微孔在二维空间是均匀分布的,但采用电子显微镜观测时,由于视野范围很小,不同视野范围内观测到的微孔数目及分布均会存在一定的偏差。表1统计的数据,电子显微镜观测视野面积总计约为0.1 mm2。模拟分析程序中也采用了0.1 mm2的面积,为减小采样的统计涨落,模拟分析程序重复采样1 000次后取平均值。在测量误差范围内,模拟分析程序的计算结果与实验观测结果匹配、符合得较好,验证了模拟分析程序的可靠性。 核孔膜已被应用于在诸多高端领域。核孔膜的孔隙率及重孔分布直接影响了核孔膜过滤器的滤除率和渗透性,因此对核孔膜表面孔隙率与重孔分布的研究具有实际应用价值。本文基于蒙特卡罗方法开发了核孔膜表面重孔分布分析程序,模拟计算了不同孔隙率下单孔、双重孔、多重孔出现概率的分布,以及重孔面积的分布情况。通过将模拟计算结果与理论推导值、核孔膜样本扫描电子显微镜观测结果进行比照,验证了模拟分析程序的准确性。 研究表明,重孔率和孔隙率这两个产品参数满足一定的函数关系,且呈正相关关系,在生产中不能独立控制。随孔隙率ηeff的增加,核孔膜表面单孔出现的概率P1单调递减,而重孔出现的概率不断增加;多重孔出现概率Pm的峰值随着重孔数目m的增加而右移。不同的孔密度n和孔径D下,重孔重叠的形态分布是相似的,PS,m概率密度分布函数也是相似的。基于m重孔的出现概率Pm和面积分布概率密度函数PS,m,得出重孔面积分布的代数解析表达式,可用于快速计算不同孔隙率下重孔面积的分布。为满足高渗透性和高滤除率的性能要求,核孔膜生产中通常需要采用高孔密度和小蚀刻孔径。利用该模拟分析程序,可优化生产中辐照注量和蚀刻孔径等工艺参数,节约生产成本和简化生产工艺。 致谢感谢欧洲核子中心吴晓伟博士关于重孔率理论计算的有益探讨。 作者贡献声明傅楗强:负责研究的提出及设计、数据的收集和整理、文章的起草和最终版本的修订。2 结果与讨论
2.1 重孔率的讨论
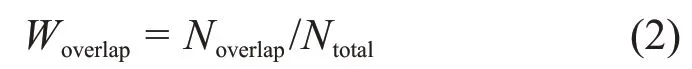

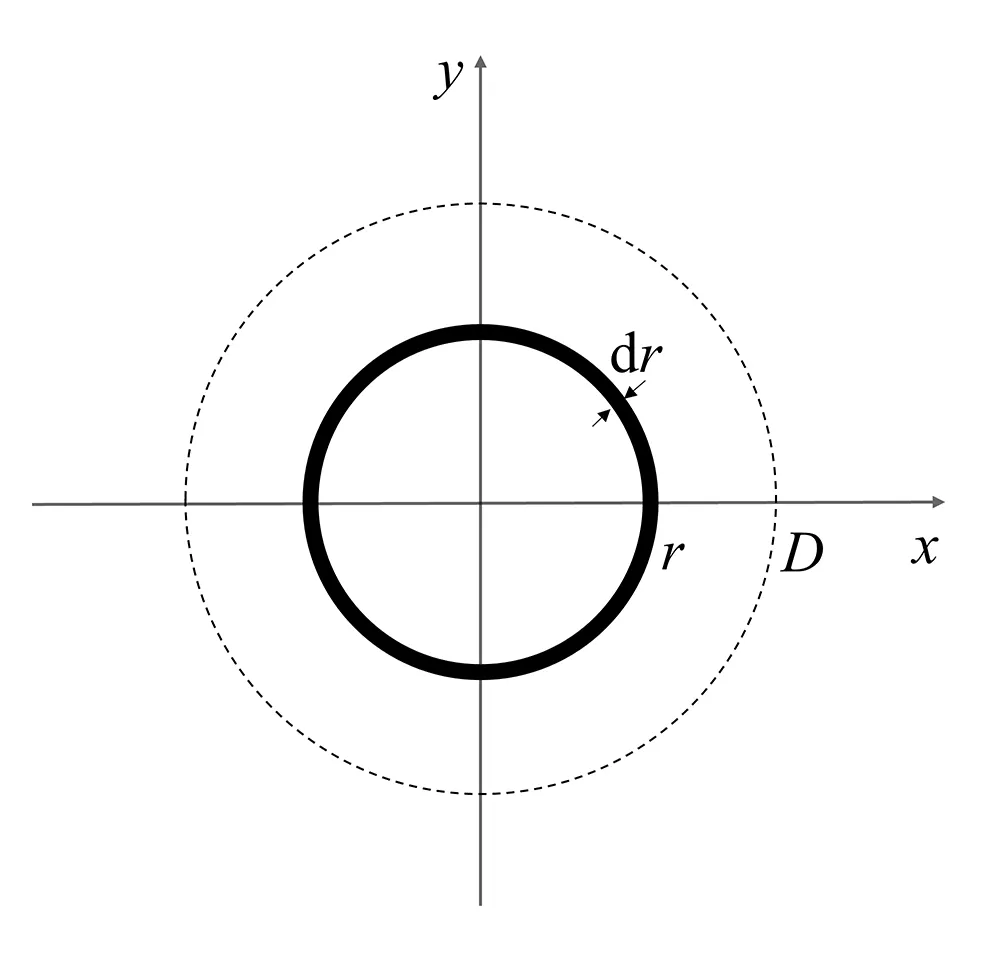

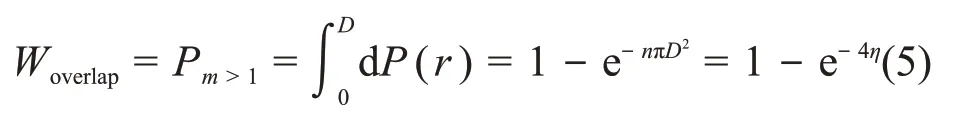
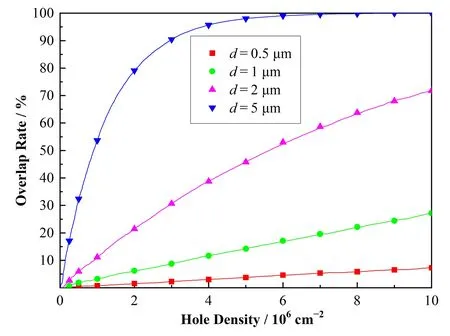
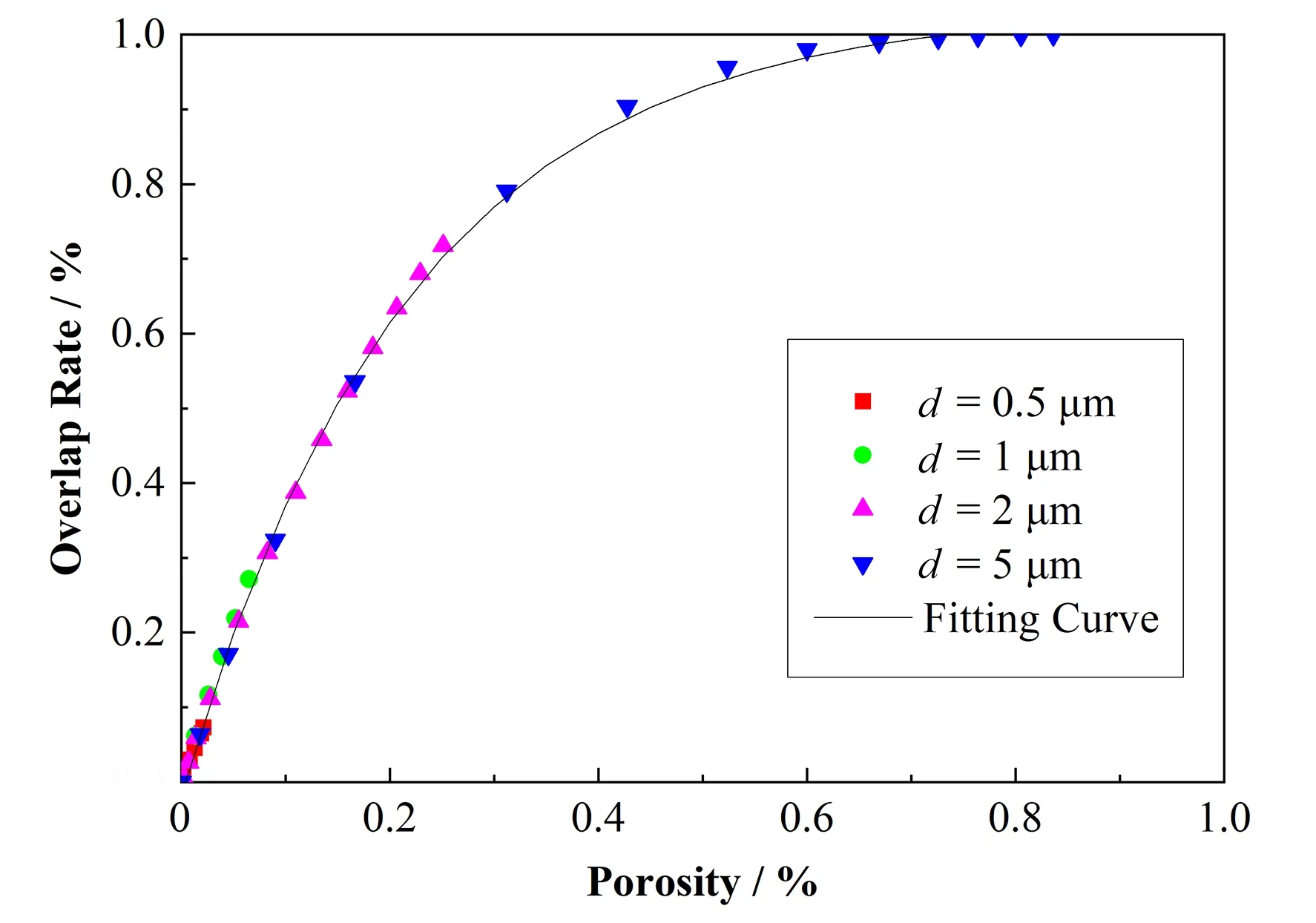
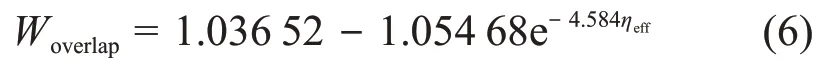
2.2 重孔分布的讨论


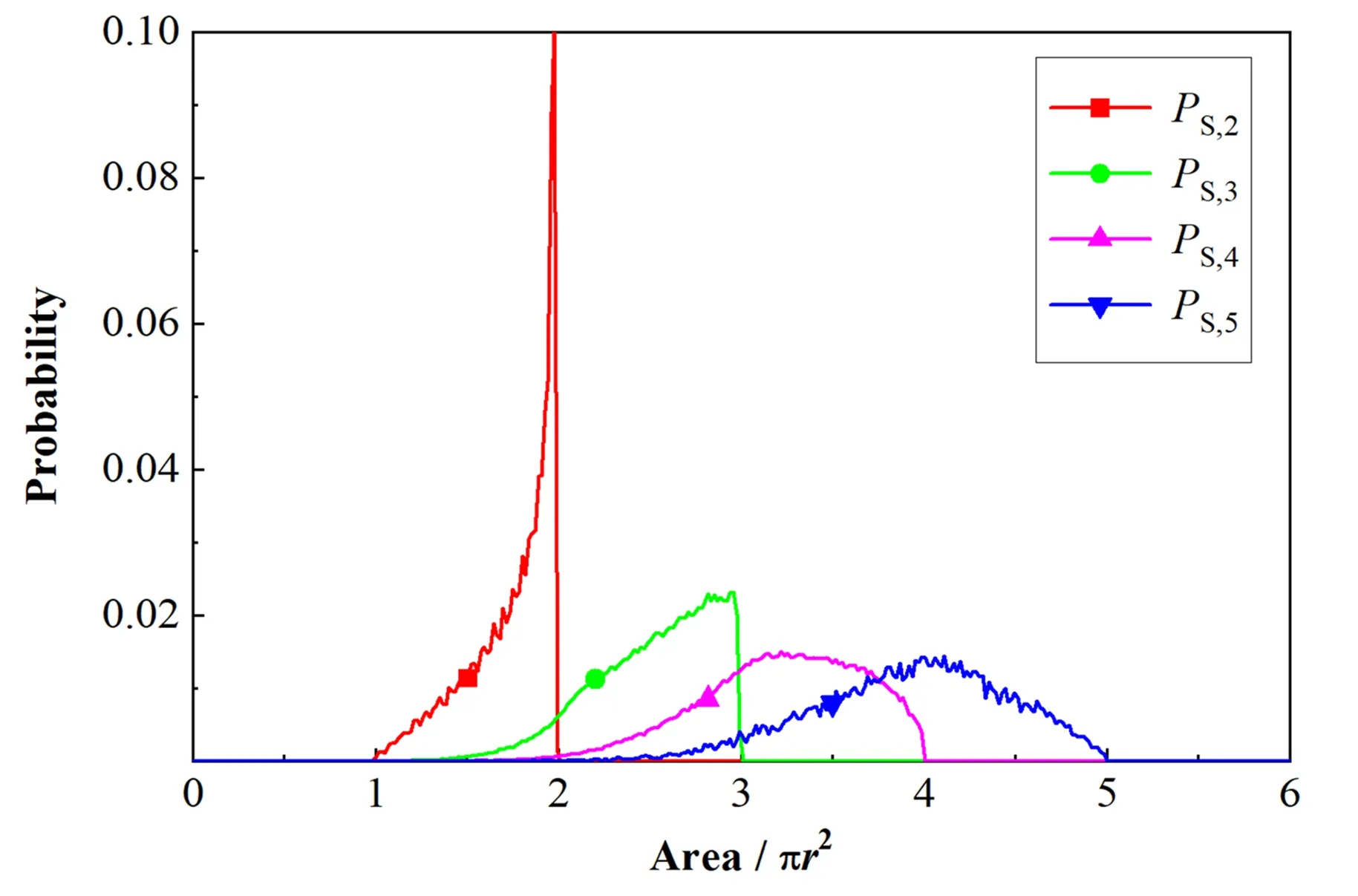
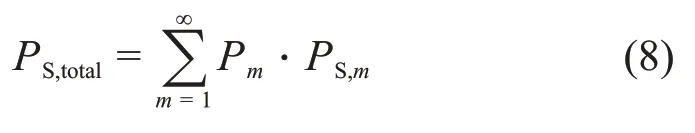


3 结语
