LaBr3(Ce)探测器点源效率函数研究

叶二雷南宏杰沈春霞许 丰史丽生

1（陆军防化学院 北京 102205）

2（安徽大学物理与光电工程学院 合肥 230601）

自van Loef等［1］在2001年首 次 研制 出LaBr3（Ce）晶体以来，经过20年的发展，LaBr3（Ce）已广泛地应用于核辐射探测领域。LaBr3（Ce）探测器具有较高的能量分辨率；光输出高且相对稳定；具有良好的时间特性；良好的线性响应能力［2‒4］。由于LaBr3（Ce）探测器的种种优点，基于LaBr3（Ce）探测器的核辐射测量仪器得到了飞速发展，在环境放射性监测［5］、γ能谱测井［6］、核电站辐射监测［7］以及无人机航空辐射监测［8］方面发挥了重要作用。

受探测器晶体尺寸和结构的影响，不同位置处点源的探测效率具有差异性。因此，计算探测器对不同角度或距离γ射线的响应函数是辐射探测的一项重要工作。郑洪龙［9］等使用蒙特卡罗方法确定了高纯锗探测器的点源效率函数，证明了该方法确定点源效率函数的可靠性与实用性；Slawomir等［10］通过数值和实验相结合的方法对就地LaBr3（Ce）γ谱仪做了角响应修正，达到了环境监测可接受的水平。徐国庆等［11］研究了LaBr3（Ce）探测器对低能γ射线的角响应，发现该探测器对低能γ射线响应随入射角度的增大呈递减趋势，为LaBr3（Ce）探测器对未知核材料的检测提供修正参考。效率函数能够消除在实际工作中因角度或距离的偏差对探测效率带来的影响，进而提高对放射性样品活度求解的精度。

基于蒙特卡罗（Monte Carlo，MC）方法的无源效率刻度技术具有快速省时、经济代价小且MC程序简单等特点，同时，其可靠性还得到了大量的研究验证［12-14］。基于此，本文针对特定尺寸LaBr3（Ce）探测器的点源效率函数做一定研究。通过无源效率刻度技术拟合LaBr3（Ce）探测器在122~1 332 keV范围的效率刻度曲线；在5~50 cm范围内拟合了LaBr3（Ce）探测器对角度和距离的修正函数。可根据修正函数确定放射性点源在LaBr3（Ce）探测器一定空间范围内任意位置处的探测效率，方便给出LaBr3（Ce）探测器的效率矩阵。还可以将点源函数通过数值积分的方式得到面源、体源的探测效率，为体源的效率刻度提供参考，可对放射性样品的活度测量、效率修正等提供可靠的技术支持。

1 理论基础与实验准备

1.1 效率刻度理论

在对放射性样品进行活度测量前，一般需要对测量的谱仪系统进行效率刻度［15‒18］，γ谱仪探测效率的准确计算是效率刻度的重要前提，实验方法可以通过处理能谱数据获取探测效率，计算方法如式（1）。

式中：ε为点源探测效率；n为全能峰计数率，s-1；A为放射源的活度，Bq；p为特征γ射线的发射率；k为测量期间放射性衰变的修正系数。由于本文在测量时间内衰变产生的影响可以忽略不计，因此按k=1来计算。

MC方法求解探测效率的基本原理是建立单个光子在给定几何结构中的真实运动历史（光电效应、康普顿散射、电子对效应），通过对大量粒子历史的跟踪得到大量随机实验值（抽样值），用统计方法计算出某一特定能量γ射线被记录下来的概率［19‒20］。在对探测器参数、源参数及相关物理参数描述完之后，计算不同位置处探测效率的过程如图1所示。

图1 MC方法计算探测效率模拟流程Fig.1 Simulation flow of detection efficiency calculated by MC method

1.2 实验准备

采用尺寸为∅3.81 cm×3.81 cm的LaBr3（Ce）探测器搭建γ能谱测量系统，晶体结构如图2所示。其中，LaBr3（Ce）探测器型号为KLB3838，晶体外部MgO反射层厚度为0.1 cm，铝制外壳为0.2 cm，探测器底部光电倍增管在建模时用玻璃（SiO2）代替，厚度为0.2 cm；配套的上位机软件为Maestro；增益为1 024道；所用标准放射性点源为152Eu、137Cs和60Co；所用的仿真软件为MCNP5，由美国Los Alamos实验室开发而成，其计算结果的准确性受到广泛认可［21‒22］。

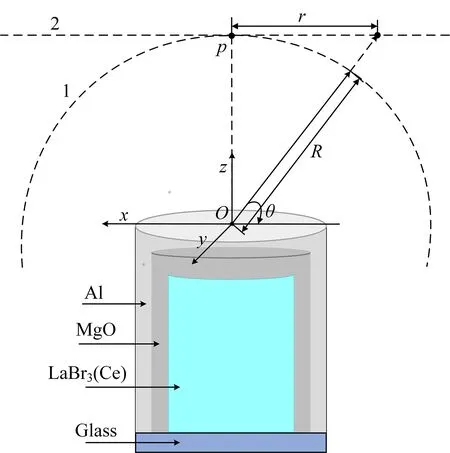
图2 探测器几何模型示意图Fig.2 Geometry model diagram of the LaBr3(Ce)detector

2 点源效率MC模拟及效率函数拟合

本文采用MCNP5模拟γ射线在LaBr3（Ce）晶体中的输运过程，使用脉冲计数卡（F8）记录γ辐射在探测器内引起的脉冲幅度，使用计数能量卡（E8）划分不同的能量区间，使用FT8卡对模拟能谱进行高斯展宽，展宽系数通过实验对该LaBr3（Ce）探测器做半高宽（Full Width at Half Maximum，FWHM）刻度后由式（2）确定。

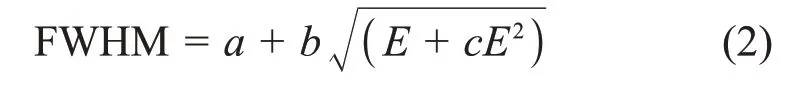
式中：a、b和c的参数分别为0.005 109、0.011 73和2.21。图3为实测谱数据在经过归一化处理后与模拟谱数据的比较，结果表明两者吻合好。

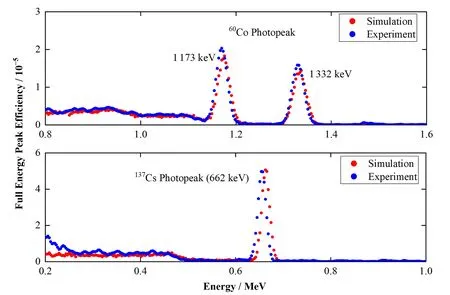
图3 模拟谱与实测谱比较Fig.3 The comparison of simulated and measured spectra

图4给出了LaBr3（Ce）探测器在距离探测器表面中心25 cm处不同能量γ射线探测效率的实验值与MC仿真值的对比，以及基于MC数据拟合的探测效率曲线，实验数据与MC仿真值的最大相对偏差不超过6%。为保证拟合函数的变化规律更加直观、准确，在峰值（约120 keV）处增添一些模拟数据点，每次模拟粒子数为108。可以看出，对于能量较低的γ射线，探测效率随能量的增大呈递增趋势，当能量大于一定值（约120 keV）时，探测效率随能量的增大呈递减趋势。这是由于探测器外部包裹材料（MgO反射层和Al壳）对低能量的γ射线衰减影响较大，随着能量的增大，这种衰减效果逐渐减弱，探测效率逐渐增大。而由于探测器的探测效率取决于光电反应过程，随着能量的不断增大，光电效应的截面会越来越小，这就导致了探测效率又随着能量的增大而减小的趋势。两种因素的叠加致使探测效率随着γ射线能量的增大呈先上升后下降的趋势，与相关研究结果一致［23‒24］。

图4 LaBr3(Ce)探测器效率刻度曲线Fig.4 The efficiency calibration curve of LaBr3(Ce)detector

3 空间点源效率分布函数

点源探测效率应是关于立体角效率、本征效率和峰总比的函数［25］，点源空间位置的改变实际上影响的是点源对探测器的空间立体角效率。本文通过MC方法研究点源在不同空间位置处探测效率的变化趋势，分析点源探测效率的影响因素，拟合出不同影响因素与探测效率的函数关系。

在图2中，O为探测器表面的中心；R为点源以O为中心在x-z平面内做圆周运动时的半径；θ为点源以R为半径沿x-z平面转动的角度，当点源位于探测器中心轴线上时θ=0；r为点源距z轴的径向距离。使用MCNP5软件分别改变r、θ、R的值来分析点源探测效率的变化情况，考虑到晶体的对称性，只在0°~90°范围内选取参考点，并对结果作曲线拟合。

3.1 θ对探测效率的影响

图5给出了在0°~90°范围内点源探测效率的变化趋势，图5中（a）、（b）和（c）分别表示R为5 cm、25 cm和50 cm时的三种情况。可以看出，总体上，探测效率随着角度的增大呈递增趋势，其最大值出现在90°；对于能量较高的γ射线，探测效率随θ的变化规律性较强，对于能量较低的γ射线，探测效率随θ的变化规律性较差，波动性较强；随着能量的增大，探测效率随θ角的变化越来越缓慢，当点源距离探测器较远时，这种变化趋势更加缓慢。在近距离（5 cm）处，1 332 keV在0°~90°范围内的最大值与最小值的相对偏差为32.2%；在远距离（50 cm）处，1 332 keV在0°~90°范围内的最大值与最小值的相对偏差为13.8%。

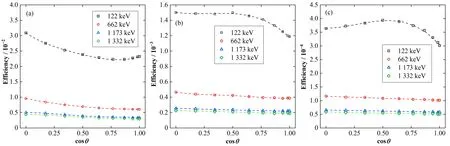
图5 探测效率随立体夹角θ变化情况Fig.5 The variation of detection efficiency with spatial angle θ

经过分析认为：当点源与探测器表面中心距离保持不变，角度改变时，点源对探测器的空间立体角效率变化很小，在θ=90°时探测器的立体角效率达到最大。由于探测器外壳对低能γ射线的衰减和探测器外壳自身的结构特点，使得在不同角度时外壳对γ射线的衰减不同，进而导致取不同θ角时，探测效率的变化会有一定的波动性。对于能量较高的γ射线，当点源与探测器的相对距离（R）增大时，点源对探测器的空间立体角减小，立体角的变化随θ角增大而表现得不明显，导致在远距离处探测效率的变化趋势也趋于一条直线。式（3）给出了探测效率与θ角余弦值的拟合函数，相关参数列于表1。

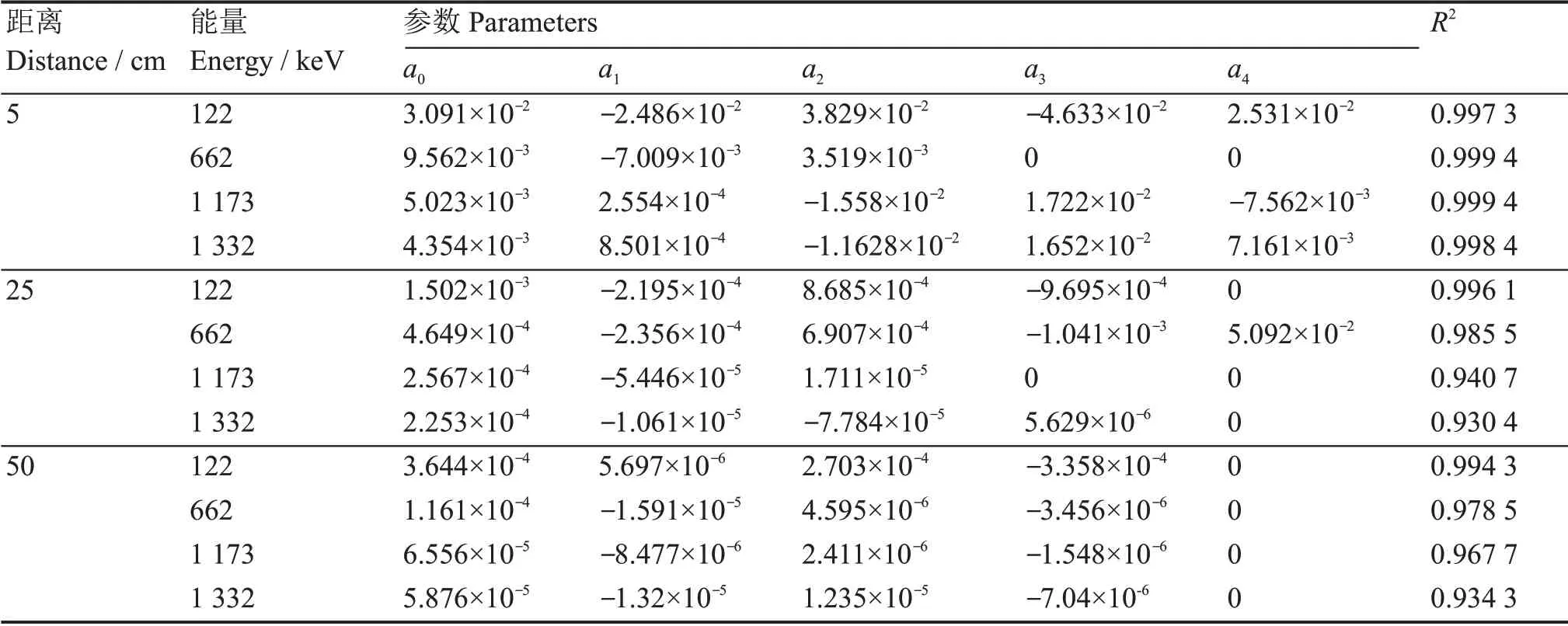
表1 探测效率与θ曲线拟合参数Table 1 Curve fitting parameters between efficiency and θ

3.2 r对探测效率的影响

在保证R值不变的情况下，使r每隔1 cm、2 cm和5 cm选取一个参考点，计算LaBr3（Ce）探测器的探测效率值，图6（a）、（b）和（c）分别表示在R为5 cm、25 cm和50 cm时探测效率随r的变化情况。可以看出，点源探测效率随着r值的增大而逐渐减小；在同一距离下，低能γ射线的变化趋势更加剧烈；随着R值的增大，探测效率随r值的增大而减小的趋势趋于平缓。分析认为，随着r值的增大，点源与探测器的相对距离逐渐增大，点源对探测器的立体角范围减小，导致了探测效率的降低。从图6可以看出，探测效率随r值的变化规律性很强，通过式（4）进行拟合，得到的相关参数列于表2，线性相关系数都在99%以上。可以很好地利用这种函数关系推导对面源、体源探测效率的计算。

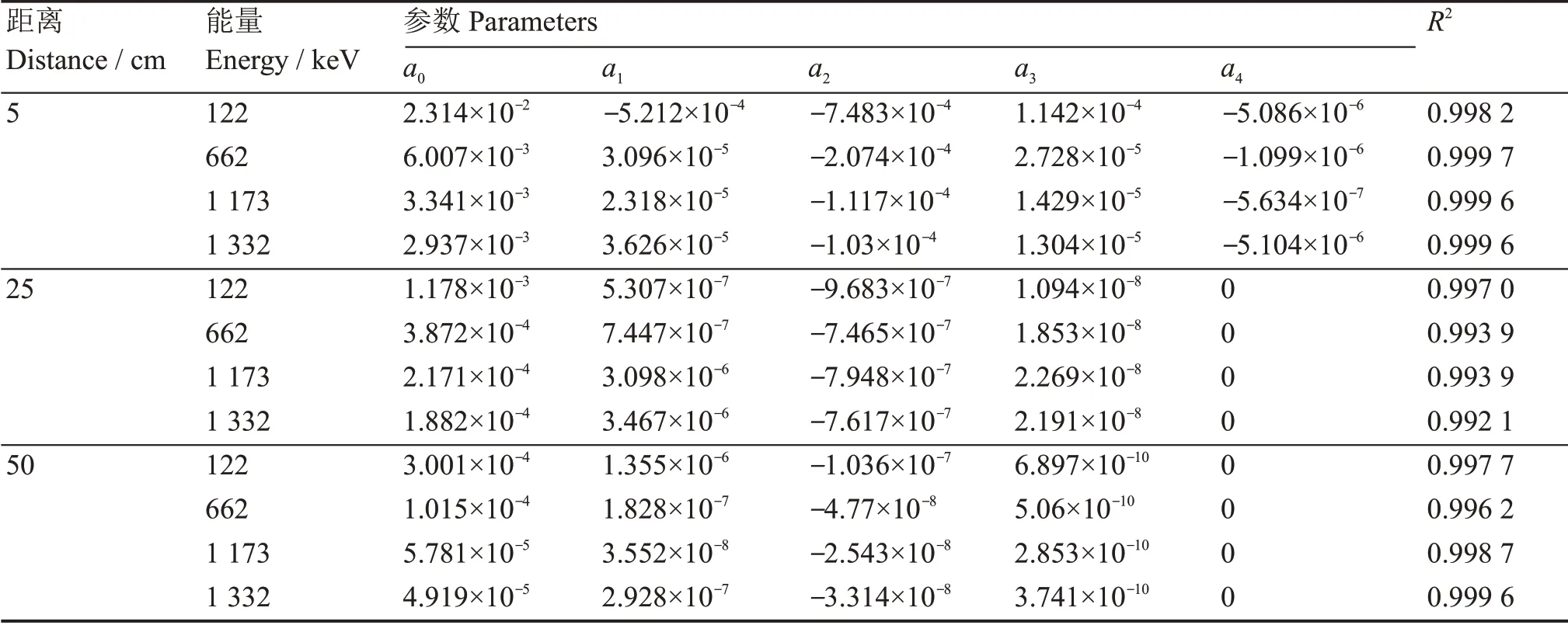
表2 探测效率与r曲线拟合参数Table 2 Curve fitting parameters between efficiency and r

图6 探测效率随r变化情况Fig.6 The variation of detection efficiency with r

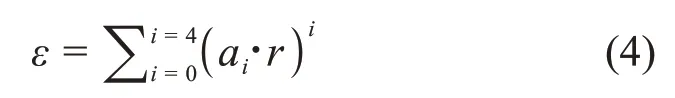
3.3 R对探测效率的影响

R值的变化将直接影响到点源对探测器的立体角，因此，本文分析三种情况下（θ=0°、45°、90°）R值的变化对探测效率的影响。从图7可以看出，探测效率随R值的增大逐渐减小，在近距离时，这种变化趋势十分剧烈，在远距离时，逐渐趋于平缓。可以认为在近距离处，立体角随着R值的增大而变化得较为剧烈，当达到一定距离时，立体角随R值的变化逐渐趋于平缓。为验证这一结论，利用式（5）计算了点源在3.81 cm LaBr3（Ce）探测器在轴向位置时的立体角效率εa，见图8。可以看出，R值的变化对立体角效率的影响与对探测效率的影响一致。利用式（6）拟合了探测效率随R值的变化函数，线性相关系数在99.9%以上，相关参数列于表3。

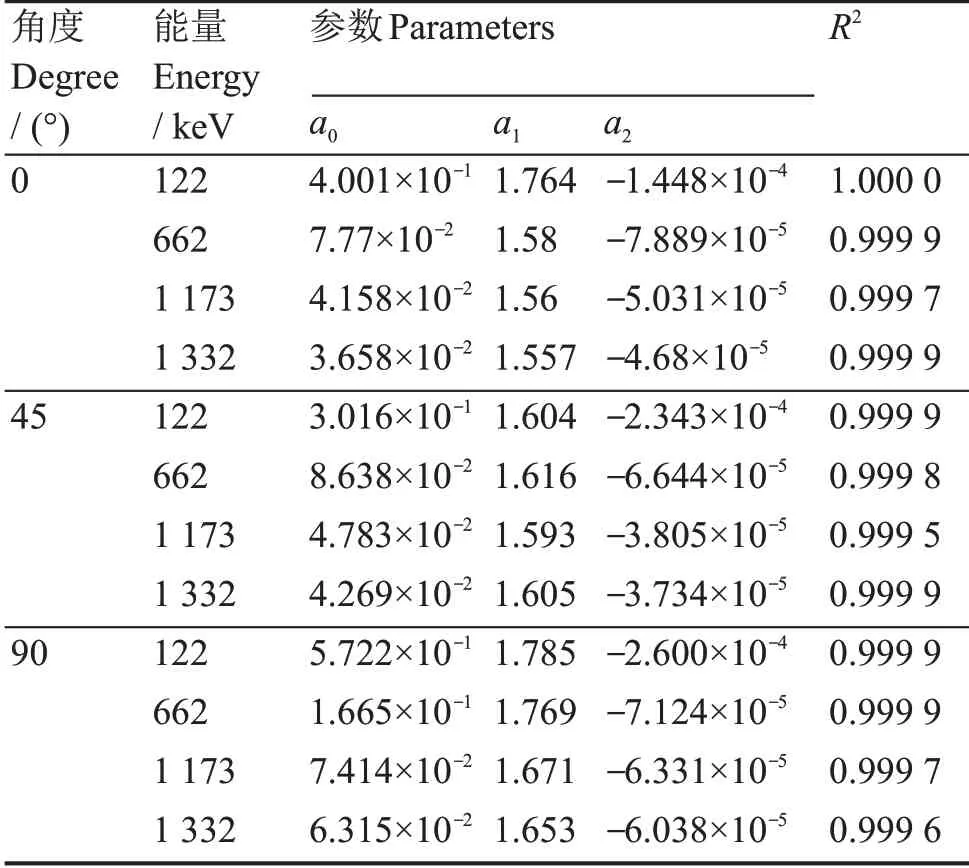
表3 探测效率与R曲线拟合参数Table 3 Curve fitting parameters between efficiency and R

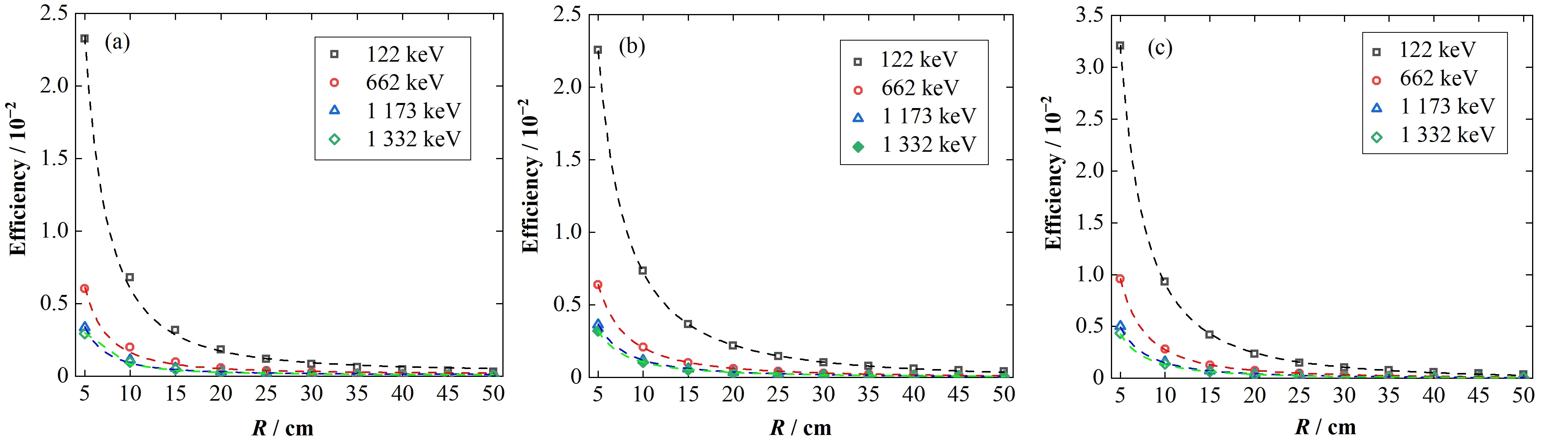
图7 探测效率随R变化情况Fig.7 The variation of detection efficiency with R

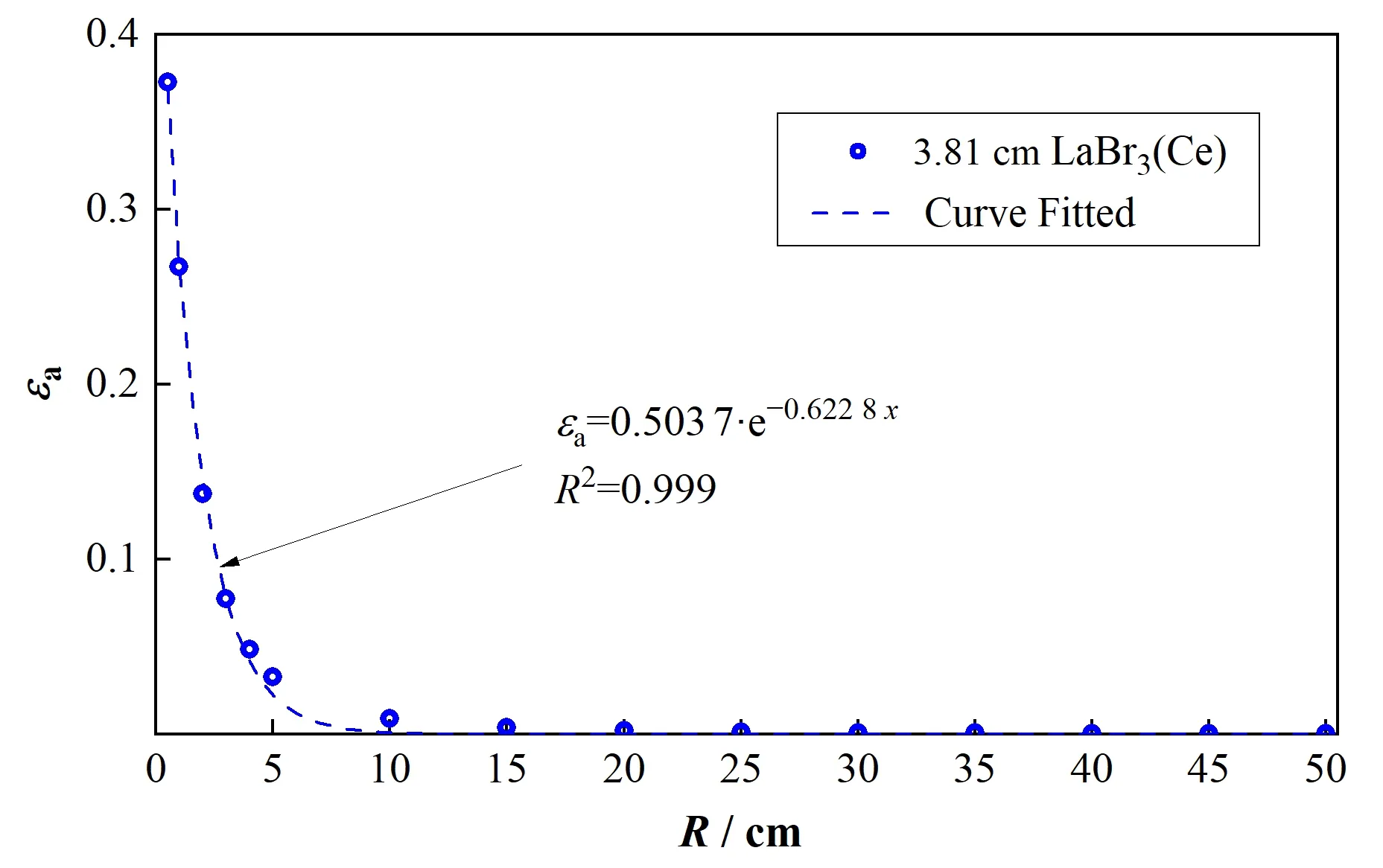
图8 立体角效率随R变化情况Fig.8 The variation of spatial angle efficiency with R

4 结语

本文通过蒙特卡罗方法模拟计算了∅3.81 cm×3.81 cm LaBr3（Ce）探测器空间不同位置处的探测效率，系统研究了点源探测效率及其随距离和角度的变化关系，得到以下结论：

当源-探距不变时，随着θ角的增大，探测效率值总体呈递增趋势，最大值出现在90°处。对于高能γ射线，随着源-探距的增大，这种趋势将逐渐变得平缓。在一定远的距离处，可以考虑用空间一点处的探测效率值来近似与之在同一圆周上其他点的探测效率值；当探测器与源之间的轴向距离和径向距离逐渐增大时，点源探测效率呈现出逐渐减小的趋势，通过函数进行曲线拟合，拟合的线性相关系数都在99%以上，可通过该函数确定空间任意位置处的探测效率，并可通过积分方法得到线源、面源和体源的探测效率；空间位置对点源探测效率的影响实际上是改变了点源相对于探测器的空间立体角，对于同一能量γ射线，当忽略探测器外壳对低能γ射线的衰减时，若点源相对于探测器的空间立体角不变，其所对应的探测效率应是不变的。

LaBr3（Ce）探测器目前被广泛应用于核辐射监测、核应急和核安保等领域，基于LaBr3（Ce）探测器的便携式仪器也正在快速发展。本研究可为基于LaBr3（Ce）探测器的核辐射仪器在放射性现场的定量测量、活度修正提供有益的技术参考，有利于核辐射探测技术的进一步发展。

作者贡献声明叶二雷：负责设计实验方案，数据仿真与数据处理，撰写论文；南宏杰：指导论文的实验工作、模型建立与论文的数据分析，提供实验器材；沈春霞：负责论文的总体规划，指导论文的写作与修订；许丰、史丽生：负责文章图表的绘制，以及参与论文的修订。