基于DIC技术的矿岩散体剪切运动特征研究

2022-09-21金爱兵姚宝顺唐坤林孙浩赵怡晴

中南大学学报（自然科学版） 2022年8期

金爱兵，姚宝顺，唐坤林，孙浩，赵怡晴

(1.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京，100083；2.北京科技大学土木与资源工程学院，北京，100083；3.中国恩菲工程技术有限公司，北京，100038)

在自然界中存在着一些散体，其本身为固体，但由于颗粒尺寸小且数量庞大，因而其运动过程中的特性类似于流体，常见于露天矿排土场边坡中[1−2]。散体颗粒的性质介于液体和固体之间，大量散体颗粒表现出来的形态与其所盛放的容器息息相关，而且它们能够从容器中流出。在一定条件下，散体颗粒的行为与液体非常相似。从理论建模的角度来看，散体颗粒更接近固体，而不是液体。散体颗粒有限的局部应变是固体变形的典型特征，而涡旋形成和无限应变是液体流动的典型特征[3]。有学者研究表明，当盛放散体颗粒的容器足够大时，散体颗粒可以视为连续介质[4]。

对于散体边坡而言，稳定性是研究的重点，散体边坡内部颗粒级配、受力情况以及局域结构受力不均匀导致边坡安全性评估难度较高[5−6]。针对这些情况，已有不少学者进行了研究。其中，李鹏越等[7]对人工堆载散体边坡与颗粒滚落进行试验，研究表明颗粒几何尺寸是影响散体边坡的重要因素；王光进等[8]通过FLAC数值模拟指出：散体边坡粗颗粒含量增加会使边坡破坏剪切面抬升。散体边坡失稳主要表现为颗粒间的剪切，剪切破坏区域随散体参数变化而变化，安全性评估的重点是确定构成边坡颗粒的力学参数等，剪切试验是获取这些参数的直接手段[9]。直接剪切试验(简称直剪试验)可以揭示边界位移问题中颗粒介质的剪切响应，重现在大规模边界位移问题(例如地震表面断层破裂)中形成的剪切模式[10]。因此，直剪试验是研究散体运动最常见的技术之一，不少学者对此进行了室内试验和数值模拟研究。其中，王子杰等[11−14]基于固结直剪室内试验和数值模拟探究了散体颗粒剪切过程中应力−应变关系、散体位移以及颗粒接触力等的变化规律，探究了影响散体抗剪能力的因素。YANG等[15]基于数值模拟研究了剪切过程中接触力各向异性特征，指出接触力各向异性在剪切过程中前期显著发展后趋于稳定，且主方向会发生逆时针旋转。刘忠强等[16−19]进行了土石混合颗粒大型直剪试验，指出粗颗粒的增加会增强散体抗剪强度、剪胀性，且粗颗粒对能量耗散以摩擦为主。在散体剪切应力−应变关系研究中，后期曲线存在“陡升”[20]、“跌落”[21]现象，LI等[22]通过直剪试验对剪应力−位移曲线波动进行傅里叶转换，指出剪切力波动会克服剪切阻力膨胀分量，粒度、法向应力、剪切率都是影响剪应力产生波动的原因。这些散体力学研究可以为散体边坡的稳定性分析提供指导，但是在散体边坡滑移面确定方面仍有局限性。散体边坡失稳后产生的剪切滑移面、滑坡量、滑移位置等仍缺乏有力支撑，因此，需要加强对散体剪切过程中剪切运动特征的研究。

在剪切运动特征研究中，董云等[23−24]采用物理试验和数值模拟研究发现：剪切面具有较强起伏程度，可用分形维数加以表征。在对单一颗粒的研究中，MACAULAY等[25]验证了散体力学方面摩擦本构，指出单一颗粒运动能力弱于散体系统惯性运动能力。CUI等[26]指出颗粒在剪切过程中会发生旋转，而旋转对剪切行为至关重要。ZHANG等[27]指出快速旋转的颗粒主要位于从剪入区到剪出区对角带上并且与力链带共轭。WANG 等[28]指出颗粒旋转的数量与旋转角速度呈高斯分布。在局部应变研究中，SUN 等[29]通过试验得出高摩擦状态下混乱度对系统稳定性的影响大于对局域结构的影响；ANGUS等[30]指出，增加摩擦会抑制局部应变区域的颗粒运动。在剪切带研究中，洪勇等[31−34]指出，在摩擦一定情况下，散体颗粒粒径对剪切带影响较大，为颗粒级配中位粒径的10～21倍。GUO 等[35]基于直剪数值模拟探究了剪切带与局部应变演变，指出非仿射位移与局部应变有显著相关性，剪切带是不可逆颗粒重分布的结果。

综上所述，人们对散体运动特性研究相对偏少且均是基于数值模拟研究，缺乏物理试验佐证，对空间位置和时间演化研究有待加强。因此，本文采用自制可视化剪切模型和数字图像相关技术(digital image correlation method，DIC)对剪切过程中颗粒的运动状态、局部应变和剪切带演化规律进行监测，探究矿岩散体颗粒基本强度特性和运动特征，结果可为散体边坡滑坡过程的相关研究提供理论支撑。

1 基于DIC的固结直剪试验

1.1 试验装置与材料

在传统散体直剪试验尤其是大型试验中，一般采用附带剪切模型的剪切仪，该装置所有部分均采用钢铁制成，在剪切试验中对散体颗粒的运动状态难以监测。因此，本试验采用YSZJ-50型岩石直剪仪搭载自制可视化剪切盒进行矿岩散体颗粒直剪试验。自制可视化剪切盒长×宽×高为300 mm×250 mm×200 mm，如图1所示。其中，可视化剪切盒正面采用钢化玻璃制成，其余三面采用不锈钢铸造，克服了传统剪切试验不可视的问题。剪切盒分为上、下两部分，下部固定其位移，在上部进行垂直方向固结加载和水平剪切，剪切方向如图1(b)所示。引入DIC技术对剪切过程中颗粒位移、旋转、局部应变和剪切带进行实时监测，拓展了DIC技术在矿岩散体领域的应用。

图1 矿岩散体可视化剪切装置Fig.1 Ore-rock granular visual shear device

试验采用河南郑州的天然状态灰黑色石灰岩，质地坚硬，单轴抗压强度为72 MPa，密度为3 150 kg/m3。根据试验要求，将散体颗粒采用方格筛进行筛分，筛分后的石灰岩散体如图2所示，选取粒径分别为5～10 mm 和10～15 mm 的颗粒进行试验。

图2 筛分后的石灰岩散体Fig.2 Limestone granular after sieving

1.2 试验过程

DIC技术的基本原理是通过对初始图片划分区域，并在后续图片中逐点寻找上一张图片中的相同位置，记录其位移差，形成位移场，并根据时间间隔计算速度场等[35]。DIC 基于散斑进行识别，散体颗粒的喷涂散斑效果较差，因此，将所有颗粒平均分成两部分，分别喷上白色和黑色油漆，再将两者均匀混合，形成散斑颗粒，克服图像识别精度低、效果差的问题，试验时，装填在可视化剪切盒钢化玻璃一侧；另外，为进一步研究剪切面上颗粒位移，选取少许颗粒喷红色油漆作为标志颗粒，放置于可视化剪切盒剪切面处。

首先，对粒径为5～10 mm 矿岩散体分别施加100，200，300 kPa 的垂直压力进行剪切，探究其应力−位移关系；然后，添加粒径为10～15 mm 的粗颗粒，使粗细颗粒质量比分别为1/5，1/4，1/3，1/2 和1，粗细颗粒混合均匀后装填至剪切盒内部，并施加200 kPa垂直压力进行试验，探究颗粒级配对矿岩散体剪切力学性质的影响。最后，采用DIC 技术对剪切过程中的颗粒位移、局部应变和剪切带进行分析。

直剪试验基本步骤为：1)安装固定剪切模型；2)装填矿岩散体颗粒；3)在模型上部添加垂直压力，到达预设垂直压力后停止加载；4)进行DIC设备空间坐标与尺寸的标定；5)添加横向载荷，同时采用DIC 记录剪切过程；6)对试验数据进行分析处理，得到局部应变以及剪切带的演变规律。

2 基于DIC的剪切特性

2.1 剪切力学性质

100 kPa 垂直压力下矿岩散体颗粒直剪试验结果如图3所示。

图3 100 kPa垂直压力下直剪试验结果Fig.3 Direct shear test results under 100 kPa vertical pressure

采用压力传感器和位移计记录剪切过程中的应力与剪切位移变化。在剪切前期，剪应力急速升高，随后趋于平缓。当垂直压力为100，200，300 kPa 时，矿岩散体抗剪强度分别为15.80，61.40 和92.02 kPa。可见，随着垂直压力增加，抗剪强度明显增加，与其他散体力学特性相同，矿岩散体抗剪强度随着垂直压力增加呈线性增大。

矿岩散体抗剪强度随粗颗粒质量分数变化曲线如图4所示。可见，随着粗颗粒质量分数增加，抗剪强度也进一步增加。这表明矿岩散体中粗颗粒质量分数增加，颗粒之间的咬合度加强，从而散体抗剪能力加强；另外，随着粗颗粒的加入，颗粒之间密度进一步提升，形成了更加致密的散体结构。

图4 200 kPa下矿岩散体抗剪强度随粗颗粒质量分数变化曲线Fig.4 Variation of shear strength of ore-rock granular with coarse particle mass fraction under 200 kPa

根据图4，对剪切峰值强度与粗颗粒质量分数进行拟合可以得到：

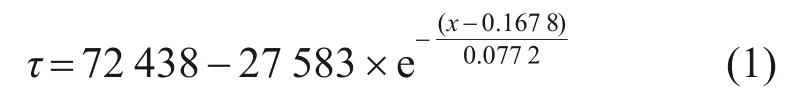
式中：τ为抗剪强度，Pa；x为粗颗粒质量分数，%。

结合图4和式(1)可知，随着粗颗粒质量分数增加，抗剪强度增加的幅度逐步减小，说明粗颗粒对矿岩散体之间的咬合度与密实度的增加作用有限。适当增加散体边坡矿岩散体粒度和对散体边坡压密可以在一定范围内增加散体边坡抗剪能力，增强边坡稳定性。另外，通过增加散体边坡密实程度和咬合度增加边坡稳定性存在局限性，因此，需要减小散体边坡可能产生的剪应力，如对边坡进行台阶化处理。

2.2 剪切运动特征

2.2.1 剪切面颗粒运动特征

在矿岩散体剪切过程中，在不同压力条件下，单个颗粒和整个矿岩散体系统的运动效果表现出相似特征，因此，以垂直压力为100 kPa下矿岩散体运动状态为例分析其颗粒运动特性。

散体标志颗粒在不同位置的运动情况如图5和图6所示。从图6可见：随着剪切位移增加，红色标志颗粒除了随着整个矿岩散体系统运动外，还因受到周围颗粒作用发生了位移和旋转(图6(a))，其中位移分为2种情况：一种是散体颗粒内部相互作用导致颗粒实际位移小于系统实际位移，二者之间的位移差称为横向削弱位移(图6(b))；另一种是受剪胀作用影响，颗粒向上下两侧发生位移，称为竖向挤压位移(图6(c))。

图5 剪切面标志颗粒运动情况分析Fig.5 Schematic diagram of sign particle rotation

图6 标志颗粒运动示意图Fig.6 Movement diagrams of shear plane marker particles

在剪切前后，剪切面上颗粒发生了旋转、横向削弱位移和竖向挤压位移，且运动强弱和运动趋势随颗粒位置的不同而有所差异。整体而言，随着到剪入口距离增加，颗粒横向削弱位移和竖向挤压位移都呈现出先减小后增加的趋势，颗粒旋转则刚好相反，则呈现出先增大后减小的趋势，即在该点颗粒的位移及旋转加速度正负发生了改变。

从图5可以看到，标志颗粒在剪切面上有1个共同的运动趋势突变点，位于距离剪入口100 mm处，即距剪入口1/3剪切面长度。剪应力驱动和散体系统阻碍作用在该位置形成交汇点，颗粒运动状态改变，这也是散体剪切过程中剪胀效应的体现，表明剪胀效应在剪切过程中对整个散体系统的影响不是一成不变的，它在剪切面上随着到剪入口距离的增加先降低后升高。另外，由剪切引起的外界能量输入是一定的，这些能量对颗粒产生压密、位移以及旋转作用。WANG 等[28]指出，在剪切过程中会产生颗粒重分布，从剪入区到剪出区结构先变简单后变复杂，结构稳定性也随之先减小后增加。由于不同位置密实度不同，产生的局部结构存在差异，结构与应力共同促进颗粒运动特征改变。

在散体边坡滑坡过程中，产生滑移剪切面上颗粒也会相对于整个滑面发生类似运动，且运动均基于滑床进行，垂直挤压位移与旋转角度也决定着滑坡的剧烈程度。在散体边坡滑坡过程中，在滑移剪切面上应该存在1个颗粒运动状态的突变点，可能与剪切运动中的至剪入口1/3剪切面长度类似，对此位置加强治理可以有效预防散体边坡发生滑坡。

2.2.2 剪切过程中的局部应变特征

与岩石的剪切破坏不同，散体剪切破坏过程由多个局部应变共同协调完成。局部应变为剪切过程中发生剪应变显著且应变集中的局部区域。局部应变的发生往往是由局部散体颗粒受到相反的力矩作用而导致的。在已有的研究中，相关学者基于局部应变表征非仿射变形的程度[36]。对于局部应变的研究，有学者通过理论计算提出了局部应变判别准则[37−38]：

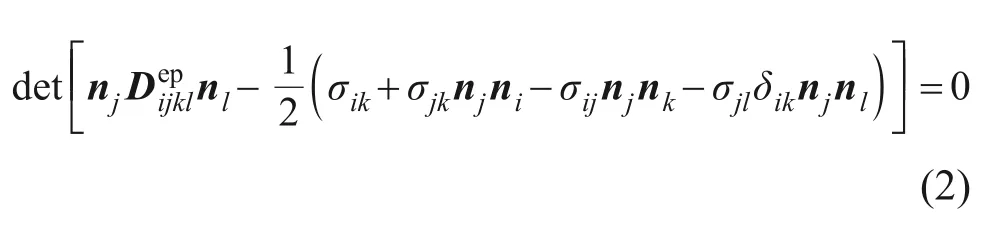
式中，ni，nj，nk和nl为剪切带的单位法线矢量；为弹塑性刚度张量；σij，σik，σjk和σjl为当前应力张量分量；δik为当前应变张量分量。

本文主要基于DIC 进行剪应变场分析，研究剪切过程中的局部应变特征。在散体剪切过程中，局部应变对剪切过程有直接影响，因此，探究局部应变的时间演化很有必要。在剪切过程中，局部应变演化规律如图7所示。从图7可见：在剪切过程中，局部应变区域逐渐从随机分布向剪切面聚拢；在剪切初期，剪切力对颗粒系统的作用力较小，局部应变主要由垂直压力压缩产生；剪切开始时，垂直压力已经覆盖全局，因此，剪应变发生区域呈现全局无规律随机分布状态(图7(a))；随着剪切力逐渐增加，剪切力对局部应变的演化主导作用增强，局部应变从剪入口区域(图7(b))向剪切面聚集(图7(c))；此后，局部应变出现贯通且基本不再发生变化(图7(d)～(f))。

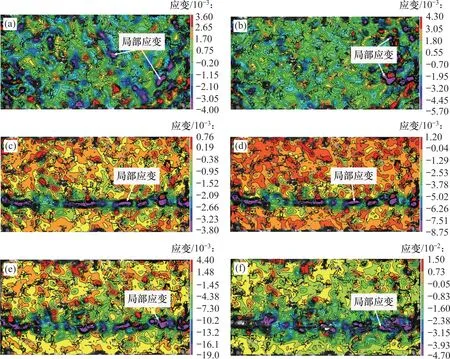
图7 剪切过程中局部应变演化规律Fig.7 Local strain evolution law during shearing

在有界区间内，局部应变发生的可能性可以用局部应变概率密度表征，概率密度具有非负性[39]。试验中，局部应变概率密度可通过DIC 技术对剪切应变定量化得出。以剪切带的最大厚度划分区域，对区域内的局部应变进行统计分析得到局部应变的时间演化规律，如图8所示。

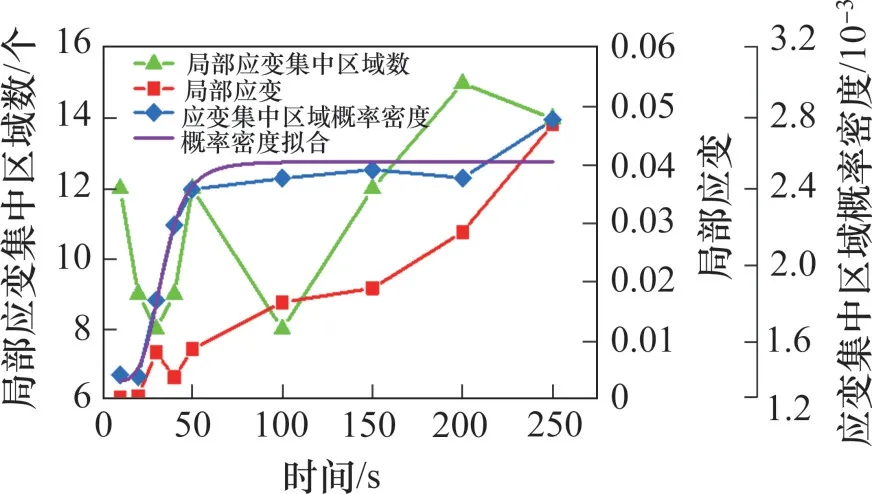
图8 局部应变时间演化规律分析Fig.8 Analysis of local strain time evolution law

在剪切面附近，发生局部应变集中区域的数量随机变化，但在粒径级配保持不变的情况下，局部应变集中区域的数量在8～15 个范围内，且局部应变及其增长率随时间逐渐增加。对划分区域内的局部应变进行统计分析，可以得到局部应变概率密度随时间推移呈现出先剧烈增长后趋于稳定的规律，其符合logistics回归模型：

式中，p为局部应变概率密度；A1为系数，取值范围为1.30×10−3±1.11×10−4；A2为系数，取值范围为2.55×10−3±6.30×10−5；t0为时间初始值；t为时间；c为指数，本模型取值范围为5.21±1.84。

由此可以推测在散体边坡滑坡的过程中，滑移剪切带附近同样会从两端开始发展到贯通的局部应变，散体边坡发生局部应变应当与剪切中发生的局部应变类似，其概率密度也当符合该发展规律，因此，在治理散体边坡滑坡时需要注意时效性。

2.2.3 基于位移等值线的剪切带形态特征

在散体剪切过程中，剪切带是因受力方向相反导致不同颗粒发生错动的区域，在剪切过程之初就会产生，且随着剪切不断发展，最终会形成固定外形特征。基于DIC 技术，剪切带随时间演化规律如图9所示。

结合图7和图9可知：在剪切初期，剪切力较小，剪切力对局部颗粒进行压密，局部区域发生位移效果明显，且分布随机性明显(图9(a))，此时，整个区域均发生局部应变(图7(a))；随着剪切进行，矿岩散体整体被压密实，剪应力主导使得颗粒位移发生在剪入口处(图9(b))，此时，局部应变主要集中在剪入口(图7(b))；随后，矿岩颗粒位移沿着剪切面贯通，位移等值线平行于剪切面，剪切盒上下两部分位移等值线出现明显差异(图9(c))，剪切带雏形形成，局部应变同样集中在剪切面附近(图7(c))；随着剪切持续进行，剪切带厚度从剪切面逐渐往两侧扩展(图9(d)～(f))，局部应变也趋向稳定(图7(d)～(f))；剪切带形成以后会保持稳定，继续试验，剪切带的厚度不会明显增加或者发生其他变形。最终，局部应变贯穿剪切面形成类似于“半梭形”的剪切带，上部分为圆弧面，其示意图如图10所示。

图9 剪切过程中剪切带时间演化规律Fig.9 Time evolution of the shear band during shearing process

图10 成型剪切带形状示意图Fig.10 Schematic diagram of shape of forming shear band

从图10可见：剪切带上部和下部形态有着明显差异，上部形态较为规则，且厚度偏大，而下部杂乱无章；另外，对于上部剪切带，最大剪切带靠近剪入口剪切带较平缓增长，到达最大厚度后，以更快的速度降低到剪切面。导致这一现象的原因是随着剪切进行，颗粒逐渐被压实，形成稳定结构，相对于右侧受到剪切力，剪出口类似于稳定边界，阻碍散体颗粒位移，因此，压实效果在剪出口尤为明显。

为进一步探究剪切带随时间演化规律，对剪切带在所选时刻最大厚度进行统计，根据DIC 处理结果，以剪切面为分割面，将剪切带分为上下两部分进行研究，结果如图11所示。

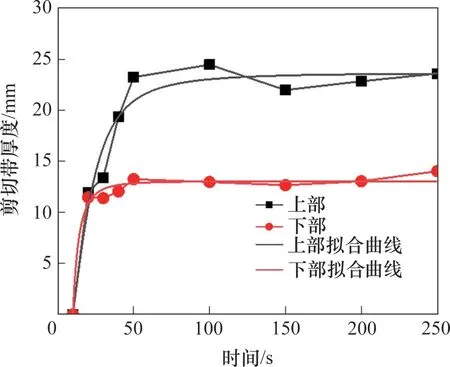
图11 剪切带最大厚度时间演化曲线Fig.11 Time evolution curve of the maximum thickness of shear band

剪切带厚度前期快速成型，后期基本保持不变，剪切带上部和下部均表现出相同规律。对其进行统计分析后发现，二者与局部应变概率密度一样，符合logistics模型：

式中：d为剪切带厚度；k1为系数，上下部分别取−0.58±1.02 和−415.01±3.19；k2为系数，上下部分别取2.37±0.13和1.31±0.04；t0为时间初始值；n为指数，上下部分别取2.26±1.09和2.56±2.79。

根据图10和11 可得：下部剪切带最大厚度约为上部剪切带最大厚度的2/5，其厚度差为散体颗粒中位径的2～3倍。粗颗粒混入对剪切带有一定程度增加，但稳定后，剪切带上下两部分最大厚度差与颗粒级配中位径的倍数关系不变。剪切带上下两侧厚度差异除受颗粒级配影响外，还受到剪胀效应影响。在剪切过程中，颗粒除了受到剪切盒影响外，还受到内部颗粒之间相互作用，针对整个散体系统去除刚性位移可以得到瞬时散体剪切位移矢量图，如图12所示。散体剪切过程中，颗粒在不同时刻的运动存在随机性，但整体而言，位于下方的颗粒有向左上方运动的趋势，即由于底部固定边界，在剪胀作用下，颗粒向上部产生挤压，这也解释了图10中剪切带上下两部分厚度存在差异的原因；且前文已经提及剪胀效应在空间分布上作用效果并不相同。另外，从图12可以发现：虽然不同位置颗粒都有往左上方发展的趋势，但位移矢量的角度不同，这进一步说明了图10中剪切带下部不规则的原因。另外，上部剪切盒受到横向压力，主导整个矿岩散体剪切过程也是影响因素之一。

图12 去除刚性位移的剪切位移矢量图Fig.12 Shear displacement vector diagram without rigid displacement

在散体剪切过程中，颗粒位移是相互协调的，具体表现为：颗粒发生平移和转动，但由于不同颗粒位置受力不均匀性，颗粒相互作用效果也有差异。靠近剪入口处，颗粒受到的剪胀效应被剪应力削弱，颗粒运动主要受到横向剪应力作用，随着与剪入口距离增加，剪应力对剪胀效应作用降低，剪胀效应进一步加强，因此，颗粒运动存在差异。

根据剪切带的时间演化规律也可大致推断散体边坡滑坡体随时间演化服从类似规律，在后续的散体边坡滑坡研究中建立滑坡体的时间演化模型，有助于确定散体边坡防治的最优时间。散体剪切会形成固定形态规模的剪切带，由此可以推断散体边坡滑坡也将形成类似于固定形态规模的滑坡体，有助于滑坡和滑坡范围的预测。