矿岩初始运动对其冲击溜井井壁规律的影响
2020-10-26路增祥吴晓旭
路增祥 吴晓旭 马 驰 殷 越
(1.辽宁科技大学矿业工程学院,辽宁鞍山114051;2.辽宁省金属矿产资源绿色开采工程研究中心,辽宁鞍山 114051)
溜井运输是金属矿地下开采的常见运输方式之一,进入溜井中的矿岩在其运动过程中与溜井壁发生碰撞会导致井壁产生损伤破坏[1-4],严重时导致井壁垮塌冒落,使溜井运输受阻,影响矿山生产的正常进行。为解决这一问题,国内外许多学者进行了大量研究,如叶海旺等[5]通过建立PFC2D数值分析模型,研究了平硐溜井系统中矿石与溜井井壁的初始碰撞位置及其冲击破坏特性;秦宏楠等[6]采用离散元方法,研究了矿石在溜矿段中的运动规律及其对井壁的冲击破坏规律,揭示了矿石在井筒中的冲击部位、冲击速度与冲击动能等之间的关系;ESMAIELI等[3]采用PFC2D数值模拟方法,研究了分支溜井卸矿条件下,主溜井井壁受矿岩冲击时的冲击速度和能量与分支溜井倾角的关系;宋卫东等[7]基于运动学分析和相似试验,研究了矿石在采区溜井中的运动规律和冲击荷载,得到了受冲击破坏的区域;任智刚等[8]基于相似性模拟试验,研究了不同地质结构下某铁矿3#溜井放矿时的冲击破坏点分布情况;罗周全等[9]针对某铅锌矿4#溜井的冲击损伤,采用MADIS-FLAC3D数据耦合技术建立了数值模型,并通过定量计算,得到该溜井受冲击的标高范围为-265.83~-292.28 m。上述研究成果为解决溜井井壁的稳定性问题起到了积极作用。
矿岩在进入溜井时具有与溜井轴线不同的运动方向和运动速度,是矿岩块在溜井中运动时与井壁产生碰撞的主要原因。为从根本上减少矿岩块在溜井中运动时与井壁发生碰撞的概率,避免矿岩块对溜井井壁的冲击破坏发生,本研究通过理论分析,并结合溜井工程实践,分析矿岩进入主溜井时所具有的初始运动方向及其对矿岩在溜井中运动规律的影响,建立了矿岩初始运动方向与矿岩块冲击溜井井壁位置之间的关系,从防止矿岩块冲击溜井井壁的角度,提出了溜井设计与生产管理的新思路。研究成果能够为分支溜井与溜井上部卸矿站设计和溜井的生产管理提供一定的参考。
1 基本假设与分析模型建立
1.1 基本假设
由于溜井倾角不同,矿岩在溜井中的运动表现为下落、跳动、滚动、滑动4种方式[1]。矿岩进入溜井时,由于卸载动能和重力势能的共同作用,其运动轨迹呈现出抛物运动轨迹。为分析矿岩在溜井中的运动规律,本研究提出几点假设:①矿岩块在溜井内运动过程中,其运动方向不会因相互之间的碰撞而改变,只有与井壁发生碰撞时才会改变;②矿岩块下落过程中的空气阻力不会对其运动速度产生影响;③矿岩块不会因其块体形状、相互碰撞等原因,而在其运动过程中产生旋转;④矿岩块发生碰撞时,不会产生质量的改变,也即发生相互碰撞时,矿岩块不会产生破裂。
1.2 分析模型
图1为金属矿床多阶段开采时常见的主溜井结构。主溜井断面形状为圆形,直径为D,分支溜井的底板与主溜井井壁相交于O点,分支溜井与主溜井的中心线夹角为90°-α。当矿岩离开分支溜井进入主溜井时,按一定的运动轨迹迅速下落,其下落的能量来源于矿岩块在分支溜井中积累的运动动能和进入溜井时刻具有的重力势能。根据已有的研究成果[6-7,10],矿岩块在溜井中下落时,经过2~3次与溜井壁碰撞,最后落入井底。

2 矿岩块在溜井中的运动轨迹
2.1 运动学分析
对于图1所示溜井结构,以O点为原点,建立了矿岩块的运动学分析模型,如图2所示。

当矿岩块离开分支溜井与主溜井的交点O时,所具有的初始速度为v0,其方向与水平方向的夹角为α,则v0在水平方向和垂直方向的分量vx和vy的计算公式为[9,11]
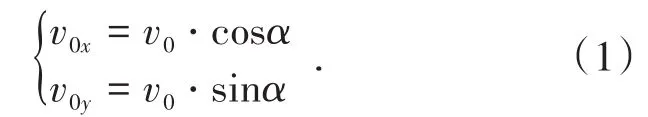
在图2所示的坐标系下,根据溜井中矿岩的运动特征,矿岩块与溜井井壁发生第1次碰撞前的任一时刻t1矿岩块所具有的运动速度为

式中,g为重力加速度,m/s2。
此刻,矿岩块离开O点距离的参数方程为
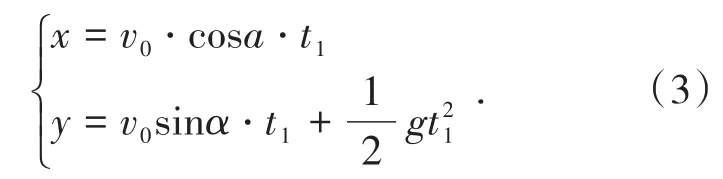
从式(3)可以得出,矿岩块在与溜井井壁发生第1次碰撞前的位移特征服从式(4)所示的轨迹方程。

2.2 矿岩块与井壁碰撞的条件与位置
在任意时刻t1,矿岩块在溜井中水平方向的运动距离为

对于任意直径的溜井,其直径D与矿岩块的水平位移量x存在的关系为

即有:

式中,x的值域为 0~D,而且只有当 x满足 0<v0⋅cosα⋅t1<D时,矿岩块在溜井中运动才不会与井壁产生碰撞。
根据这一条件,并结合轨迹方程(式4)可以得出矿岩块第1次与溜井井壁发生碰撞时的最大深度h1为

根据能量守恒定律,可求得矿岩块第1次冲击溜井井壁时的瞬时速度v1为

式中,h1为O点至A点的垂直距离,m。
2.3 矿岩初始运动速度影响因素
分析式(2)和式(3)可知,决定矿岩块水平位移量x的参数为vx和t1两个变量,其中vx取决于矿岩块的初始速度v0和α角大小。
理论上讲,α∈(0°,90°),因而cosα的值域为1~0。对于图1所示的溜井结构,随着α取值的增大,cosα值越小,也即vx值也越小。当v0和t1保持不变时,增大α,可以降低vx,因而能够减小水平位移量x。
从矿岩进入溜井时具有的运动能量角度分析,不考虑矿岩在分支溜井中的运动阻力和运输设备卸矿时赋予的动能时,根据能量守恒原理,可得:

式中,m为矿岩块的质量,kg。
由式(10)可得:

3 矿岩初始运动对其冲击井壁规律的影响
矿岩对溜井井壁的碰撞是井壁产生损伤破坏的根本原因[12],式(8)给出了矿岩块第1次与溜井井壁发生碰撞的位置。从式(8)可以看出,碰撞点的位置与溜井直径D、矿岩进入溜井时的初速度v0及其方向以及方向角α大小有关。
3.1 初始速度对碰撞点位置的影响
对于特定直径的溜井,当D=5m时,为研究碰撞点位置随v0和α变化的规律,根据溜井设计时α的可能取值范围,按每2.5°的增量计算了不同v0条件下的h1值,结果如图3所示。
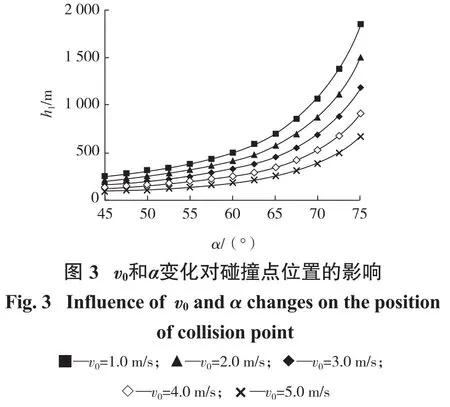
分析图3可以发现,碰撞点的位置与矿岩块进入溜井时的初始速度的平方呈反比关系。具体来说:①同一初始速度v0条件下,随着α角增大,碰撞位置距矿岩块进入溜井的距离h1不断加大;反之,这一距离减小。②不同初始速度v0条件下,当α角不变时,初始速度v0越大,碰撞位置距矿岩块进入溜井的距离h1越小;反之,这一距离越大。
3.2 溜井直径对碰撞点位置的影响
当矿岩块进入溜井的初速度v0=1m/s时,通过式(8)计算得到了不同溜井直径条件下,碰撞点位置h1与矿岩块初始运动方向α的关系曲线,如图4所示。
分析图4可知:①同一溜井直径条件下,随着α角增大,碰撞位置与矿岩块进入溜井的距离h1不断加大;反之,这一距离减小。②不同溜井直径条件下,当α角不变时,随着溜井直径增加,碰撞位置与矿岩块进入溜井的距离h1不断加大;反之,这一距离减小。

4 减小碰撞概率的措施
减小矿岩块与溜井井壁发生碰撞的概率,是减轻溜井井壁受到冲击破坏的重要途径。根据矿岩块与井壁发生碰撞的运动学原理以及上述研究结果,在溜井设计与建设时,可以采取的措施有:①增大矿岩块进入溜井时初始运动方向与水平面的夹角;②减小矿岩块进入溜井时的初始速度;③增大溜井直径。
5 溜井设计与管理的新思路
(1)改变矿岩块进入溜井时的运动特征。确保溜井结构的合理性[13-14],有利于减小矿岩块进入溜井后对井壁的冲击。对于图1所示的溜井结构,B、h0和α都是由设计给定的,主要是根据工程位置的岩体稳固程度,确定合适的卸矿站中心线与溜井的距离B,以保证工程系统的稳定性。因此,根据上述研究成果,溜井设计时可通过改变溜井结构,改变矿岩块的运动轨迹,避免矿岩下落时对溜井井壁造成冲击。
(2)减小矿岩块进入溜井时的速度。高速运动的物体具有较高的冲击动能。当矿岩块以较高的速度进入溜井时,一旦与溜井壁产生碰撞,则会对井壁产生较强的损伤破坏作用。因此,降低矿岩块进入溜井时的速度,能够显著改善矿岩块在溜井中的运动状态,减小其与溜井壁产生碰撞的概率。
(3)降低溜矿段的空井高度。溜井放矿实践中,不能满井放矿,是造成溜井井壁受冲击破坏的原因之一[15]。根据溜井的使用特点,确定合理的空井高度,有利于发挥溜井的使用功能,同时也能有效防止井壁受到矿石运动的冲击。根据式(8)计算得到的矿岩块第1次碰撞井壁前的下落高度h1。溜井放矿管理中,控制溜矿段的空井高度H不超过h1,可有效降低矿岩块与溜井井壁碰撞的概率。因此,可得到空井高度的计算公式为
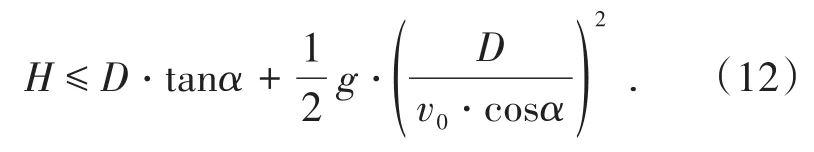
溜井生产管理过程中,严格控制溜井底部的放矿速度,建立溜井中料位与底部放矿的联锁控制机制,确保空井高度H不超过式(12)的计算结果,能够有效避免溜井上部卸矿时,矿岩块对溜井井壁的冲击,对溜井井壁受冲击破坏起到预防作用。
6 结论
(1)矿岩进入溜井时的初始运动方向对于矿岩块冲击井壁的位置影响较大,选择合适的分支溜井倾角、改变溜井上部卸矿站底部结构,能够有效改变矿岩进入主溜井的初始运动方向,进而影响到矿岩块冲击溜井井壁的位置,减小其冲击井壁的概率,有利于减轻对井壁的冲击损伤程度。
(2)通过运动学分析,建立了矿岩块在溜井中运动的轨迹方程,确定了矿岩块运动过程中与溜井井壁发生碰撞的条件,推导出了矿岩块第1次与溜井井壁发生碰撞时的碰撞位置计算公式。
(3)矿岩块与溜井井壁碰撞位置的影响因素主要有溜井直径D、矿岩块进入溜井时的初始速度v0及其方向角α。当D和v0保持不变时,随着α增大,碰撞位置h1越大,反之,h1越小;当D和α保持不变时,随着v0增大,碰撞位置h1越小,反之,h1越大;当v0和α保持不变时,随着D增大,碰撞位置h1越大,反之,h1越小。
(4)溜井工程设计时,适当增加溜井直径,选择合适的溜井结构,降低矿岩块进入溜井时的速度,能够降低矿岩块与溜井井壁的碰撞概率,有利于减轻溜井受冲击破坏的程度。
