超快过程中电子激发效应对γ−LiAlO2损伤的影响研究
2022-09-21何南燐庄慧慧杜启明严觉民程新路
何南燐,何 翠,张 娥,陈 静,庄慧慧,杜启明,严觉民,程新路
(1.武警警官学院,四川,成都 610213;2.核工业西南物理研究院,四川,成都 610041;3.四川大学 原子与分子物理研究所,四川,成都 610065)
超快脉冲激光照射到晶体表面时,首先把能量传递给晶体的电子子体系,诱导靶材产生大量很高温度的自由电子,此时电子能量达到几个电子伏特,电子被加热到大约104K,而晶格仍处于常温,致使整个电子晶格体系处于非平衡状态,产生电子激发效应,即冷晶格现象[1].随后通过电子和声子的能量交换转移为晶格的热量.在此非平衡状态下靶材会产生一些平衡态下没有的性质,例如声子挤压[2]、固−固相变[3]及非热熔化[4]等.
在国际热核聚变实验堆(ITER)产氚包层中,采用含锂氚增殖剂与中子反应生成氚来保证其燃料的“自持”,即通过以下反应来进行氚增殖:
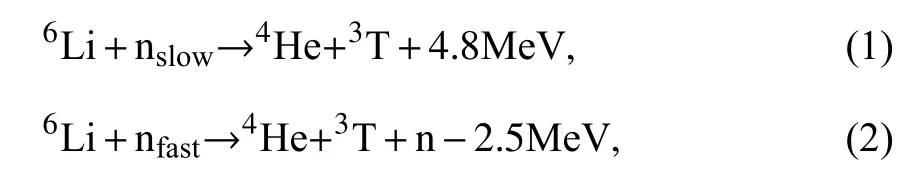
式中,nslow、3T 分别为慢中子、氚原子,nfast为快中子.
作为含锂陶瓷,γ−LiAlO2可作为未来聚变反应堆产氚包层的主要氚增殖剂候选材料[5],因此对于γ−LiAlO2材料离子和激光辐射影响的研究就显得极其重要.目前,已有较多关于γ−LiAlO2材料的研究.Marezio[6]使用普通的电子XRD−3 分光仪测得了γ−LiAlO2的晶格常数.Wu 等[7]采用基于密度泛函理论(DFT)的从头算方法对γ−LiAlO2晶体的结构性质、弹性性质和电子结构进行了理论研究.Tour 等[8]利用声学脉冲回声技术测得了γ−LiAlO2的弹性常数.Noda 等[9]在氧离子辐射实验中发现γ−LiAlO2没有明显的带吸收现象,且测得其能带宽度大约为4.8 eV.Qiu 等[10]发现在20 keV 离子束诱导下LiAlO2的冷光光谱出现7 个发射带,并证明这种现象与辐射损伤有关.Jiang 等[11]研究了He 辐照下γ−LiAlO2的结构演化和氚扩散,表明He辐照下温度为573 K 时γ−LiAlO2单晶中Al 子晶格变得相对无序,同时观察到注入离子温度提高到573~773 K 后H 扩散和Li 损失.理论上,Tsuchihira等[12]运用分子动力学方法对LiAlO2晶体的辐射损伤过程进行了详细的说明.中子、电子、X 射线、γ 射线和能量子等辐射源对γ−LiAlO2晶体结构影响的研究已有很多.关于超快辐射下电子激发效应对其结构及物理性质影响的理论研究较少.
本文基于第一性原理分析了不同电子温度条件下γ−LiAlO2声子频率曲线,以及电子激发效应对晶体的弹性性质、热力学性质和电子态密度的影响.
1 计算方法和理论细节
基于密度泛函理论(DFT),使用VASP (Vienna ab initio simulation package)程序包[13]计算γ−LiAlO2的声子谱和弹性模量.计算中采用projector-augmented wave (PAW)[14-15]方法描述电子与离子之间的相互作用,使用广义梯度近似GGA[16]中的Perdew and Wang scheme (PW91)方程来考虑交换关联效应,所有计算中平面波截断能设置为550 eV,几何结构采用 2×2×2的超胞.结构优化时布里渊中采用以Gamma 点为中心的方法自动产生11×11×11的K 点网格,以保证电子激发效应下精确计算电子自由能和体系总能量,利用不同电子温度表征电子激发效应强度[17].而且,计算设置了足够可用的占据态,即使在高电子温度时电子都有足够多的占据态.力常数计算中设置了总能量收敛的最大误差为10−8eV,所有参数测试都为收敛.声子频率和态密度计算时采用 5×5×5 K 点网格,采用准简谐近似的方法结合声子频率w=(q,l)和 声子态密度g(w)得到材料声子热力学性质(亥姆霍兹自由能F、内能En、定容比热Cv和声子熵S),其计算公式[15-16]为:

其中,n表示每个原胞中的原子数,h表示普朗克常数,kB表示波尔兹曼常数,T为晶格温度,使用PHONOPY 程序计算得到热力学关系.此外,利用晶体结构的弹性模量得到不同电子激发条件下的德拜温度 ΘD[17-18].

根据Debye Lindemann 理论,通过德拜温度可计算出材料的熔化温度:(A由晶体结构密度和原子的质量决定).
2 结果与讨论
2.1 电子激发条件下晶体γ−LiAlO2 的晶格动力学研究γ−LiAlO2属于正单轴晶体,其晶体结构可以描述为Li+和Al3+交替占据在氧四面体的中心,形成P41212[5]的空间对称群,每个原胞包含16 个原子,如图1 所示,Wyckoff 的4(a)位置由Li 和Al占据,8(b)位置由O 占据.基态时,我们首先对结构优化得到总能量最小时的平衡晶格常数.原胞晶格参数和原子坐标都会得到优化直到结构平衡.如表1 所示,我们优化得到电子温度Te=0 eV 时的晶格常数与实验值[5],和其它理论值[6,20]都符合得很好.然而,当我们增加电子温度时晶格常数呈现减小的趋势,从表1 中可看出,电子温度Te为5 eV时的晶格常数比基态时约小2.6%.
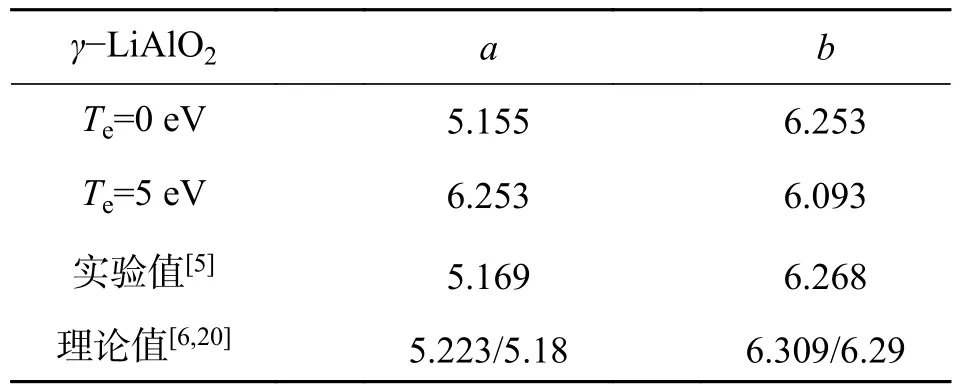
表1 γ−LiAlO2 晶格常数的计算值与实验值及理论值的对比及其 Te=5 eV 时的变化值Tab.1 The calculated lattice parameters of γ−LiAlO2 at ground state and their comparisons with experimental and other theoretical values,and the variation of γ−LiAlO2 at Te=5 eV

图1 γ−LiAlO2 的晶体结构Fig.1 Crystal structure of γ−LiAlO2
在此基础上,为进一步研究γ−LiAlO2在不同电子激发下晶格动力学稳定性,我们计算了γ−LiAlO2在不同电子激发下的声子谱.如图2 所示,γ−LiAlO2晶体每个原胞中的16 个原子共有48 个声子模式,其中3 个声学支,45 个光学支.基态时,声子频率f分布曲线如图2(a)所示,并没有出现虚频,表示γ−LiAlO2晶体动力学稳定.当电子温度在0~2 eV 时声子频率几乎保持不变,电子温度继续增大后声子频率出现明显的降低,但未出现虚频,当电子温度达到5 eV 时声子频率f开始出现负值,说明电子激发对整个体系的势能面产生了一定的影响,此时γ−LiAlO2晶体已经不稳定,如图2(b)所示.

图2 基态及Te=5 eV 时γ−LiAlO2 的声子色散曲线Fig.2 The phonon spectra of γ−LiAlO2 at ground state and Te=5 eV
2.2 电子激发效应对晶体γ−LiAlO2 电子结构及性质的改变高能离子或超快激光与靶材相互作用过程中,靶材电子被激发,在几十飞秒时间尺度达到电子温度Te,随后能量从电子传递到离子,随着电子温度的增加,态密度(DOS)被改变.为了更深入地理解电子激发效应对γ−LiAlO2晶体的影响,我们计算了不同电子温度下的电子态密度NE[21-22].从图3 可以看出,基态时,γ−LiAlO2晶体的能带宽度为4.93 eV,这与Wu 等[7]使用LDA、GGA 分别计算的值4.64 eV、4.83 eV 刚好吻合.而随着电子温度的增加能带间隙逐渐减小,在费米能级处态密度带隙消失,说明靶材料的共价键明显被削弱,逐渐显现出金属性质.Te=0 eV 时,电子态密度的价带分为2 部分:−17.21~−15.81 eV,−5.26~0 eV.随着电子温度的增加,Te=5 eV 时,价带部分变为−3.78~−3.23 eV,−0.84~−4.25 eV.
为了更清楚地描述电子激发效应对靶材的影响,我们分别计算了基态和Te=5 eV 时γ−LiAlO2晶体的电子分波态密度,如图4 所示.基态时,总电子态密度价带部分主要由O s 贡献,而导带部分主要来源于Al s/p 轨道.当电子温度增加到5 eV 时,对总电子态密度的贡献不仅来源于O s,还有O p 和Al s/p,且O p 的贡献反而比O s 大,费米能级附近主要由O s/p 和Al s/p 轨道决定.此时总电子态密度的带隙消失,说明随着电子温度增加,γ−LiAlO2晶体经历熔化转变到金属态.这与前部分计算的声子频率在Te=5 eV 时发生结构变化一致.

图4 Te=0 eV 和Te=5 eV 时 γ−LiAlO2 晶体总电子态密度及分波电子态密度Fig.4 The calculated total and partial density of states of γ−LiAlO2 at Te=0 eV and Te=5 eV
2.3 电子激发效应对晶体γ−LiAlO2 弹性性质的影响利用弹性常数Cij可以直接描述晶体的弹性性质.晶体γ−LiAlO2具有3 个独立的弹性常数(C11,C12,C44),基态时满足波恩稳定准则[23-24]:B>0,C′>0,C44>0,其中体模量B=(C11+2C12)/3 以及弹性剪切常数C′=(C11−C12)/2.如图5(a)和5(b)所示,我们计算了γ−LiAlO2在不同电子温度下的弹性模量和熔化温度Tm.可以看出γ−LiAlO2的弹性模量和德拜温度在0 eV 到2 eV 的电子激发作用下几乎保持不变,但当电子激发进一步增大时开始出现明显下降.值得注意的是当电子温度达到5 eV 时,γ−LiAlO2的弹性剪切常数已不满足波恩稳定准则,说明此时γ−LiAlO2晶体已不稳定.这与2.1 中计算得到的电子温度为5 eV 时声子谱出现虚频的结果一致.对于γ−LiAlO2,我们得到的熔化温度从基态时的1 973 K 逐渐降低,电子温度为5 eV 时Tm从4 eV 时的1 589 K 徒减到268 K.

图5 γ−LiAlO2 晶体弹性模量、德拜温度ΘD 及熔化温度Tm 随电子温度的变化Fig.5 The calculated elastic properties of γ−LiAlO2 at different electronic temperature.
2.4 电子激发对晶体γ−LiAlO2 热力学性质的影响结合声子频率、声子态密度和方程(1)~(4),我们研究了不同电子温度下γ−LiAlO2的热力学性质(声子自由能F、声子内能En、声子熵S和声子定容比热Cv),结果如图6.计算中采用准谐近似,由于不同温度下所有振动本征值已被考虑,因此忽略声子之间的非谐效应.
如图6(a)所示,声子自由能−晶格温度(F−T)曲线随着电子温度的增大而整体下降.当电子温度从0 eV 增加到2 eV 时,声子自由能基本不变,而随着电子温度继续增加曲线下降越来越明显.电子温度一定时,声子自由能随晶格温度增加而逐渐减小.此外,图6(b)给出了不同电子温度下的声子内能−温度(En−T)曲线,同样,电子温度从从0 eV 增加到2 eV 过程中,声子内能变化不大,此后随着电子温度增加内能减小,而电子温度一定时,内能随晶格温度增加而增大.
熵S和定容比热Cv是热力学中2 个重要的物理量.如图6(c)所示,随着电子温度的增大,S−T曲线整体抬升,电子温度从0 eV 增加到2 eV 过程中,并没有明显影响,当电子温度从3 eV 增加到5 eV时,S−T曲线整体抬升速度越来越快.在电子温度一定时,声子熵S随晶格温度增加而增大.因此,随着电子温度增加,声子振动加剧,声子熵S曲线整体抬升,体系混乱度增大,也就是电子激发效应使得γ−LiAlO2晶体稳定性减小.与2.1 中电子激发效应使得靶材稳定性降低所得结论一致.计算中,仅考虑了声子振动对熵的影响,忽略了电子的贡献.
最后,我们研究了电子激发效应对声子定容比热Cv的影响.图6(d)给出了不同电子温度下声子定容比热−温度曲线(Cv−T),一定电子温度下,晶格温度增加,声子定容比热增大,随着电子温度增大,Cv−T曲线整体上移.电子温度从0 eV 增加到2 eV过程中,声子定容比热基本不受其影响,当电子温度从3 eV 增加到5 eV 时,曲线整体上移速度明显加快.当晶格温度大于1 200 K 时,声子定容比热趋于一个定值,电子激发效应及晶格温度的变化对它的影响可以忽略.

图6 计算得到不同电子温度下γ−LiAlO2 晶体声子自由能F、声子内能En、声子熵S、声子定容比热Cv 曲线Fig.6 The calculated phonon free energy F,phonon internal energy En,phonon entropy S,phonon heat capacity Cv of γ−LiAlO2 at different electronic temperature.
3 结论
本文研究了超快过程中电子激发效应对γ−LiAlO2晶体损伤的影响.基态时晶格常数的计算结果与实验符合得很好,当电子温度增大时晶格常数有减小的趋势.电子温度在2 eV 以下时整个布里渊中声子色散分布曲线都为正值,并且弹性模量和德拜温度几乎保持不变.随着电子温度的增加德拜温度和熔化温度逐渐下降,声子熵也逐渐增大,体系混乱度增大,同时,能带间隙逐渐减小,在费米能级处态密度带隙消失,说明靶材料的共价键明显被削弱,逐渐显现出金属性质.而当电子温度增加到5 eV 时,声子频率开始出现负值,总电子态密度的带隙消失,晶体经历熔化转变到金属态,弹性剪切常数降为负值,体系已不满足波恩稳定准则,此时晶体结构受到破坏性损伤.
综上所述,超快过程中电子激发效应在2 eV以下时对γ−LiAlO2晶体的损伤可以忽略.但电子温度超过2 eV 后,γ−LiAlO2的损伤程度逐渐增大,且在电子温度达到5 eV 时晶体结构受到明显的破坏.本文可为研究电子激发效应对γ−LiAlO2晶体的影响提供有意义的参考.
