低填方钢波纹管涵洞受力变形特性及垂直土压力计算
2022-09-21吴冠庆岳夏冰阴增亮
吴冠庆, 魏 进, 岳夏冰, 阴增亮
(长安大学 公路学院, 陕西 西安 710064)
钢材具有抗拉、抗压、质量轻、延性强、抗剪性能优越等特点,波纹钢板作为一种具有空间薄壳柔性结构,正逐渐被应用于公路桥涵的施工中[1].由于钢质波纹管是一种柔性管材,能更好地应对地基的不均匀沉降现象,减少涵洞不均匀沉降引起的桥头跳车、路面开裂等病害[2].在我国的公路建设中,钢波纹管涵因其施工速度快、工期短、适应变形能力强及造价低廉等优点被广泛应用在填方路段[3].
对钢波纹管涵洞受力变形特性进行了研究,文献[4-6]通过现场试验及有限元分析土-结构模型.Kang等[7]提出钢波纹管属于半柔性钢管,管弹簧模型确定管涵的极限承载力.Sargand等[8]对现场6座低填方钢波纹管涵洞安装测量仪器及静载试验,结果表明低填方钢波纹管荷载评价方法偏于保守.Yeau等[9]通过现场试验研究了俄亥俄州39座公路波纹钢板的管涵性能,可知管涵尺寸、回填土高度及弹性模量是影响波纹钢板受力性能的主要因素.Liu等[10-11]对施工过程中关键部位的受力与变形进行了测试,建立有限元模型,模拟了钢波纹管在填土过程中的受力行为,得出波纹管曲率范围内的应力发展规律.Zhou等[12]采用ANSYS软件对波纹钢管与土体的相互作用进行了数值模拟与现场试验对比,发现计算结果的相对误差较小.褚夫蛟等[13]通过现场测试及数值模拟研究了上部不同填土高度下钢波纹管涵洞的力学特性.
管涵垂直土压力计算公式一直是岩土工程界的热点问题,早在1913年,Marston[14]率先推导了管涵垂直土压力计算公式,提出了管涵土压力计算方法.Spangler[15]和曾国熙[16]对Marston理论进行了充实与完善,做了大量试验与分析修正.Tao等[17]提出了一种能精确计算上埋式涵洞顶部土压力和填方土压力系数的数值模型.
对涵洞的应用调研中发现上述方法是否适用于低填方沟埋式钢波纹管涵结构尚有争议,而且管涵顶部垂直土压力设计计算过程过于理想化、简洁化及施工方法存在盲目性,导致计算不够准确.钢波纹管受力、变形及土压力的研究多集中上覆填土较高的情况,其受力-变形规律不具备广泛应用,同时低填方回填动态过程中谷顶之间的应力发展规律的分析也不够充分.鉴于此,本文基于现场试验和理论计算研究了钢波纹管涵受力与变形特性及周围土压力的变化规律,推导了一种合理的沟埋式低填方管涵顶部垂直土压力计算公式,并通过有限元进行验证.研究为公路钢波纹管涵设计与施工提供参考和理论依据.
1 工程概况及试验工况
依托陕西省某公路改扩建工程,现场试验所采用的波纹管涵洞直径为4 m,长度为27 m,波长为200 mm,波高为55 mm,厚度为4 mm,轴向设置1%横坡,与路基中线相交约70°.基础及管涵两侧回填10%灰土,采用机械夯实楔形部位.钢波纹管涵几何尺寸及现场拼装如图1所示.

图1 钢波纹管涵拼装图Fig.1 Installation of the steel corrugated pipe culvert(a)—实物图; (b)—尺寸图.
钢波纹管两侧回填土初始工况为工况1,填土过程中共分为17个工况,各工况土的压实度和容重分别为96%和19.7 kN·m-3,如图2所示.
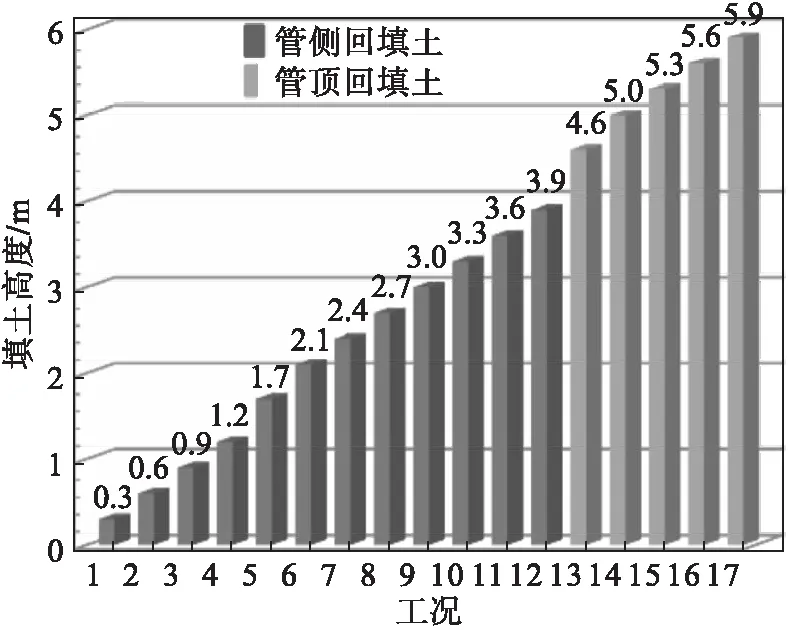
图2 试验工况Fig.2 Test working conditions
2 试验方案设计
2.1 应变及变形布设方案
钢波纹管涵的波长(mm)如图3所示.选取行车道和硬路肩分界线处作为钢波纹管涵上的应变、变形试验断面,其位置距离路基中线7.75 m,平面位置如图4所示.
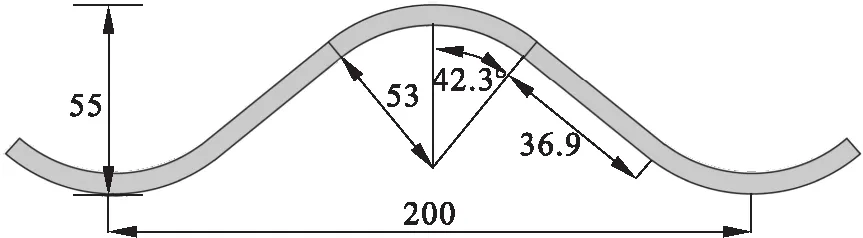
图3 波长图(单位:mm)Fig.3 Wavelength diagram(unit:mm)
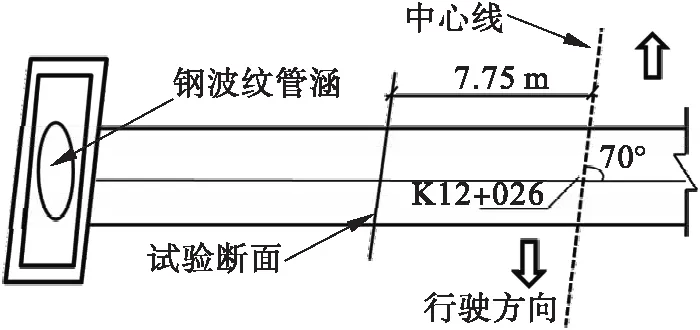
图4 钢波纹管涵试验断面布置图Fig.4 The test section of the steel corrugated pipe culvert
2.1.1 试验断面内外侧应变片布设方案
为测量钢波纹管内外应变规律,对试验断面内、外布设应变测点,如图5a所示.由于应变沿轴线近似对称分布,测点区选取试验断面内、外各一半.试验断面从内部顶点1处开始每隔30°布置1个测点,共7个测点,外部布置5个测点.管涵的波峰、波谷处应变片按“T”字形布置,如图5b所示.应变片在布设过程中应检查是否完整无损,测点表面清洗干净,贴片时应变片背部涂胶均匀,贴片完成后,对测点采用环氧树脂覆盖进行防水防潮,以便提高应变片的测量精度和使用寿命.

图5 应变片测点布置及安装Fig.5 Layout of the strain gauge measuring points and their installation(a)—应变片测点编号; (b)—应变片布置安装实物图.
2.1.2 试验断面变形测点布置
为测量钢波纹管的变形特性,在选取的试验断面布置水平和竖向两支YH02-J20型收敛计,如图6所示.
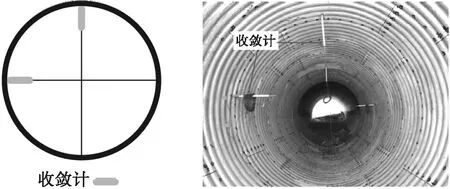
图6 试验断面变形测试布置及安装Fig.6 Layout of the deformation testing devices and their installation
2.2 土压力测试方案
选取试验断面,在钢波纹管外周从顶点起每隔30°及距管顶1 m和2 m处各布置一个土压力盒,共布设9个,编号T1~T9.在布设过程中,管涵与土压力盒间应铺设5 cm厚的细沙,以保证土压力盒受力均匀,测点布置如图7所示.
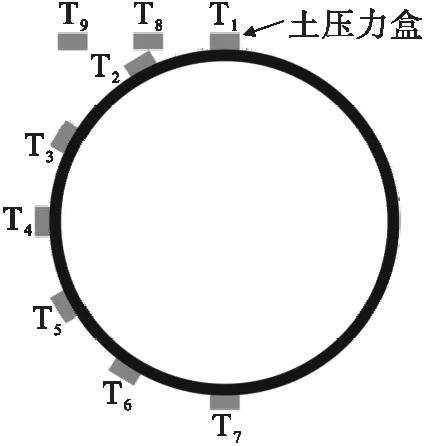
图7 土压力盒布置Fig.7 Layout of the earth pressure cells
3 试验结果及分析
3.1 试验断面应变结果及分析
3.1.1 内部轴向应变规律
试验断面内部7个测点的波峰、波谷处轴向应变分布如图8所示.
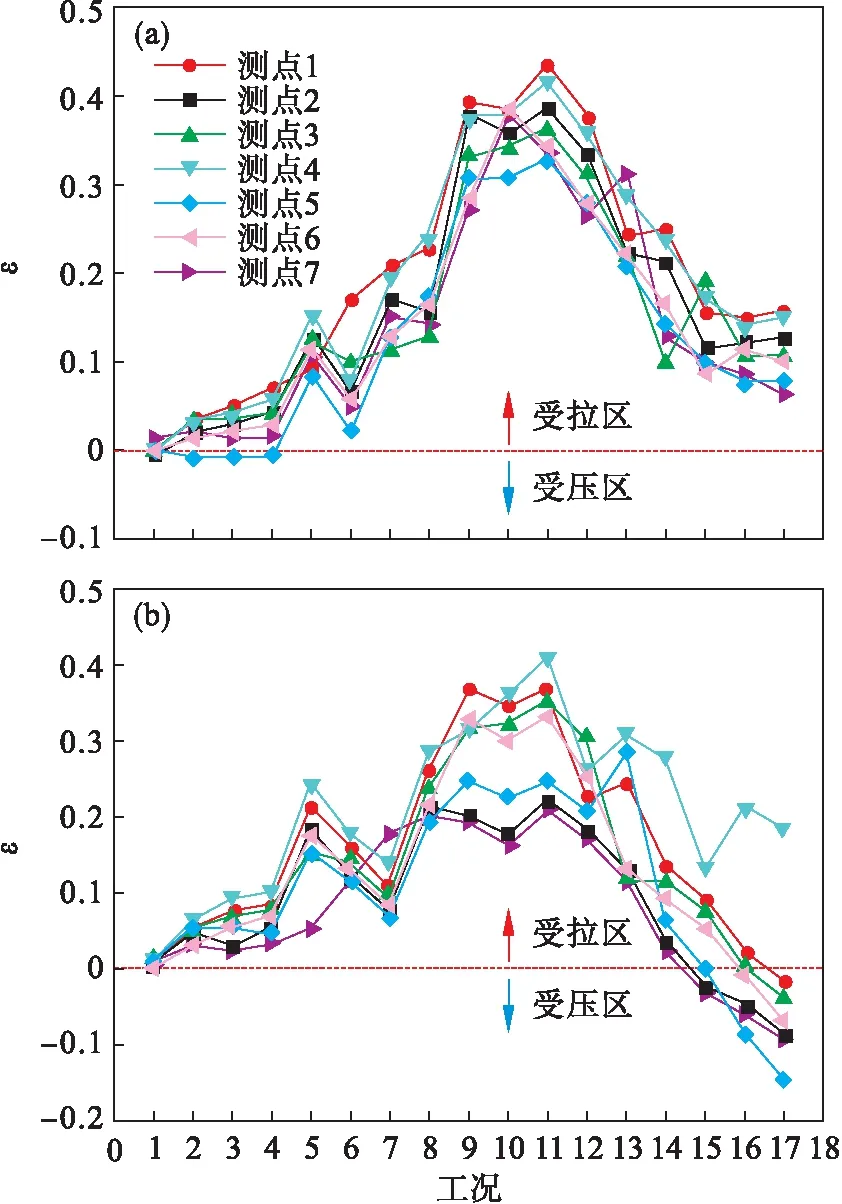
图8 试验断面内部轴向应变分布Fig.8 Inside axial strain distribution of the test section(a)—波峰; (b)—波谷.
内部各测点的轴向应变呈波动性抛物线变化.填土完成后,波峰、波谷的最大值都出现在填土高度3.6 m处,且都出现在测点1,其值分别为0.431和0.383.波谷处最大轴向应变出现在管侧测点4,为0.407.这说明波峰、波谷处的最大轴向应变出现在不同位置.填土完成后,波峰、波谷的最小值出现在不同的测点处,其值分别为0.069(管涵底部测点7)、-0.146(管涵侧面测点4)及-0.148(管涵侧下部测点5).填土完成后,波峰处的各测点为受拉状态;波谷除测点4外,其余测点为受压状态;波侧除测点1外,其余测点全为受压状态.由以上结果可知,钢波纹管涵整体上在填土完成后,波峰处呈受拉状态,波侧和波谷处呈现受压状态.
3.1.2 内部切向应变规律
填土过程中,波峰和波谷内部7个测点的应变分布如图9所示.
由图9可知,管涵内部测点切向应变呈波动性变化,波峰和波谷的最大值出现在工况11,其值分别为0.474,0.507.填土完成后,波峰和波谷的最大切向应变都出现在测点6,其值分别为0.291,0.176;最小切向应变都出现在管涵侧部测点4,其值为别为0.176,-0.244.填土完成后,波峰和波谷各测点多数都处于受拉状态,且波峰的切向应变比波谷的大了20%左右.
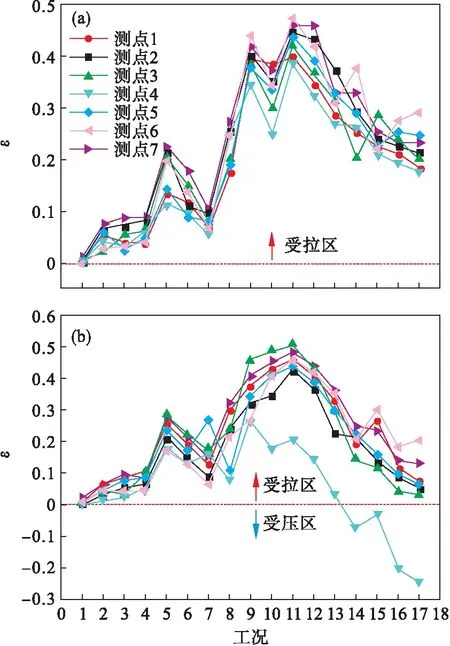
图9 试验断面内部切向应变Fig.9 Inside tangential strain distribution of the test section(a)—波峰; (b)—波谷.
3.1.3 外部轴向应变规律
管涵在两侧及上部填土荷载过程中的波峰、波谷外部测点的轴向应变分布如图10所示.
由图10可知,外侧轴向应变整体上随填土高度的增加先增大后减小,其中波谷处波动性较大.波峰、波谷的最大轴向应变在管侧填土3.6 m处,其值分别为0.61,0.393.填土完成后,测点12的波峰达到最大值,为0.334,最小值在管侧测点8,其值为-0.205.波谷在填土完成后,最大轴向应变出现在管侧测点8,为0.286;最小值在测点12处,为-0.274.管涵外部测点波峰处的轴向应变多数为受拉状态,随填土的增加,波峰侧的测点8由受拉转为受压状态.波谷处管涵侧斜上部分由受拉转为受压,其侧斜下部分始终处于受拉状态.
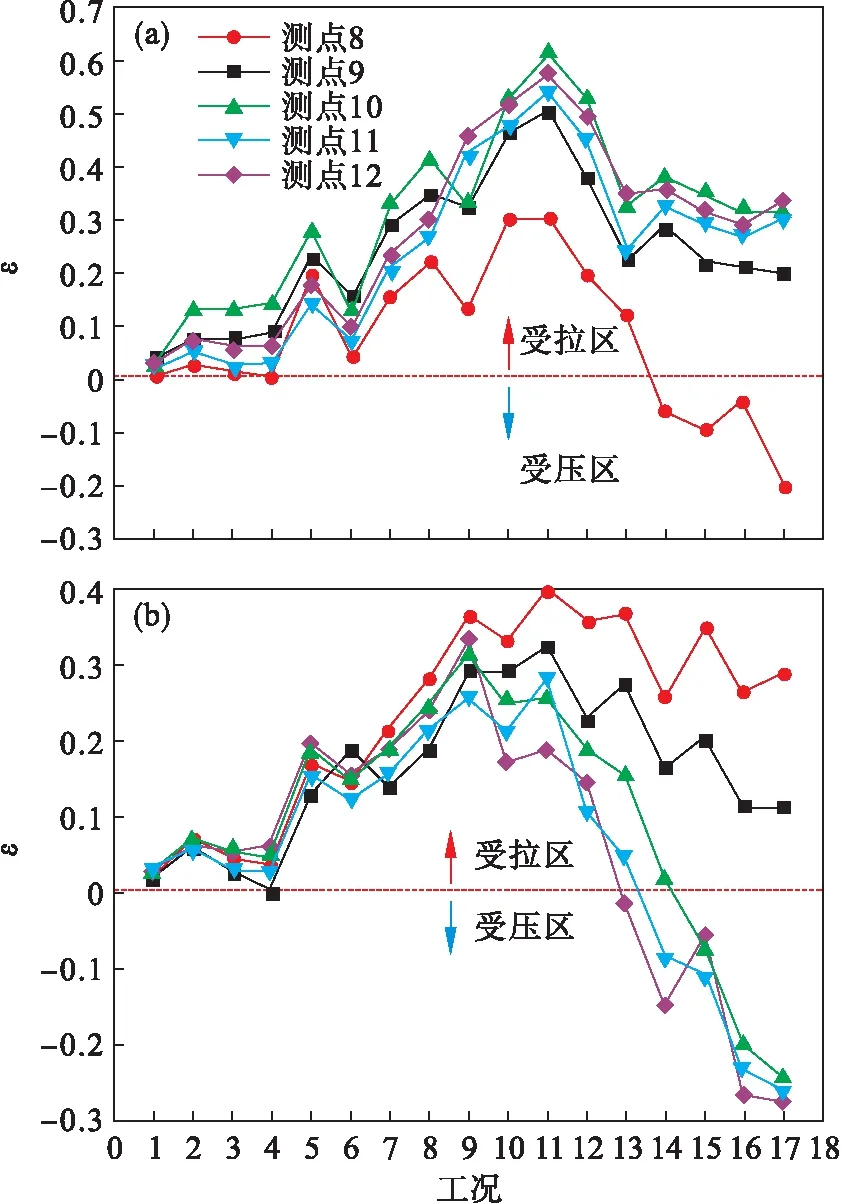
图10 试验断面外部轴向应变分布Fig.10 Outside axial strain distribution of the test section(a)—波峰; (b)—波谷.
3.1.4 外部切向应变规律
管涵外部测点的切向应变分布如图11所示.由图11可知,波峰和波谷测点的最大切向应变分别为0.493,0.388,波峰出现在工况11,波谷出现在工况9,这是由于填土过程中力度不均所引起.填土完成后,波谷测点切向应变下降幅度比波峰处大,下降幅度最大约为79%(测点8).波峰、波谷最小的切向应变分别出现在测点12,11,两者位置相差30°.总体上,钢波纹管侧承受较大拉应变,管顶承受较小拉应变.
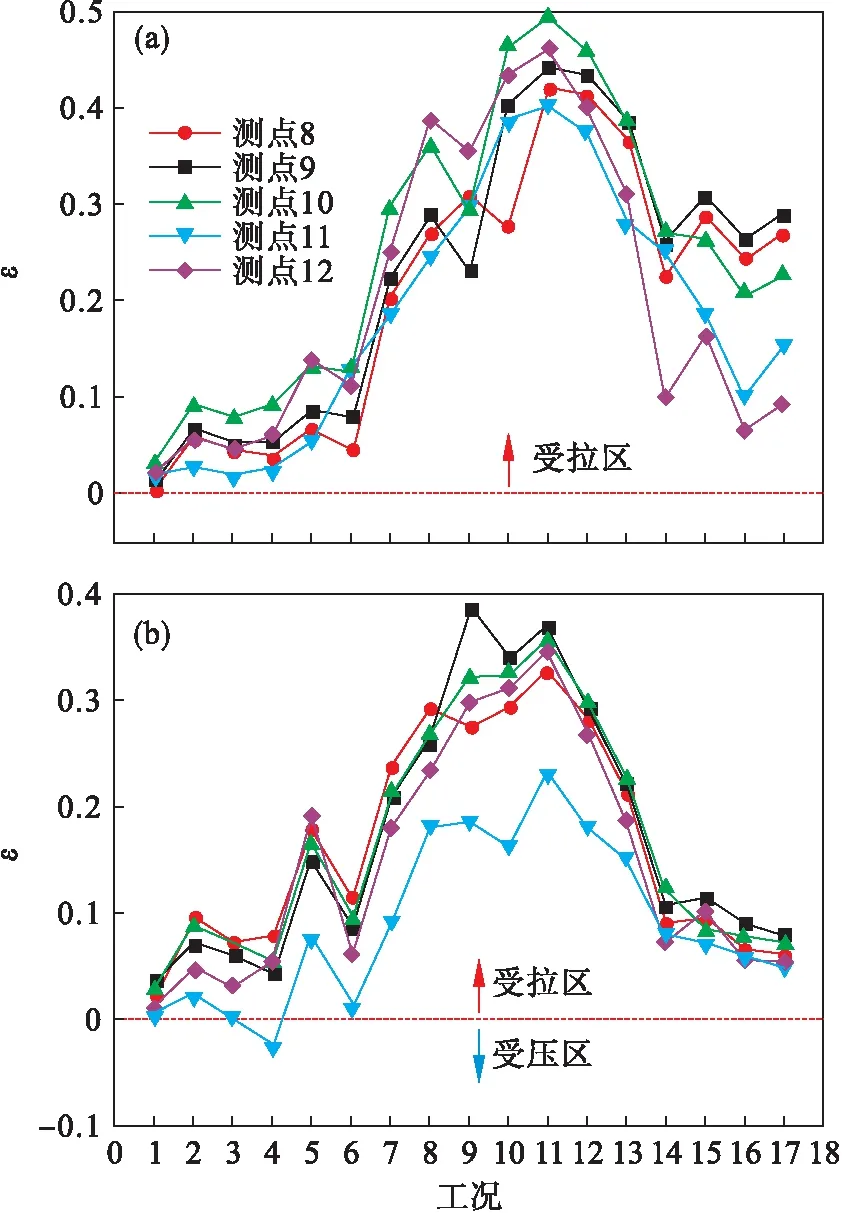
图11 试验断面外部切向应变分布Fig.11 Outside tangential strain distribution of the test section(a)—波峰; (b)—波谷.
3.2 试验断面变形结果及分析
钢波纹管截面变形随填土的规律如图12所示.由图12可知,管涵的水平向和竖向变形随管侧填土的增加逐渐变大,在工况1~工况5变形幅度较大,工况6~工况17变化趋势较为平缓,其中工况13~17呈逐渐变小的趋势.这说明填土初期,对钢波纹管涵水平向和竖向的变形影响较大,随填土的进行,水平向和竖向变形在工况13出现峰值,分别为27.2,-24.6 mm.在工况5变形发生突变,这是由于管侧填土突然增加使管侧承受的压力快速增加所引起的.从工况13开始,管涵水平向和竖向变形开始缓慢减小,原因是管顶随填土荷载的增加,使钢波纹管的水平和竖向受到压缩,导致管涵变形减小.填土完成后,由于管顶填土厚度较小,管涵顶部所提供的荷载不足以抵抗管涵两侧填土荷载对管涵的挤压作用,即管涵截面变形呈竖向椭圆形.
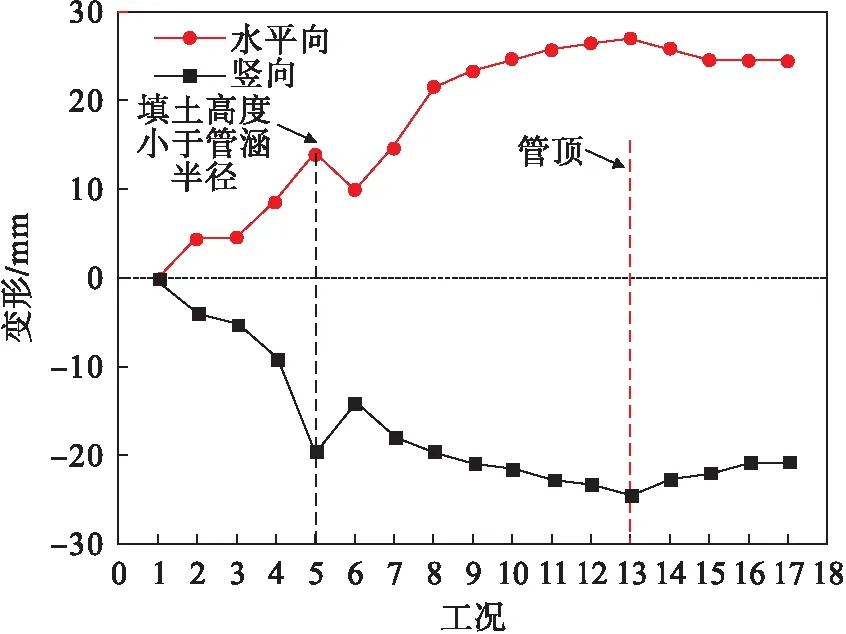
图12 钢波纹管涵变形规律Fig.12 Deformation rules of the steel corrugated pipe culvert
3.3 试验断面土压力试验结果及分析
3.3.1 管顶平面土压力分析
填土完成后,管顶土压力分布规律如图13所示.由图13可知,管顶平面土压力随填土高度的增加而增大.在填土较低时,实测土压力值与土柱法计算值基本一致.随填土高度的不断增加,实测土压力值与土柱法计算值的差距逐渐变大.填土完成后,最大土压力和最小土压力测点分别出现在T1和T9.管顶的土压力大于管侧的土压力,这是由于在填土初期,管侧的填土对管涵上部的土体产生向下的拖曳作用,导致管顶产生附加压力.
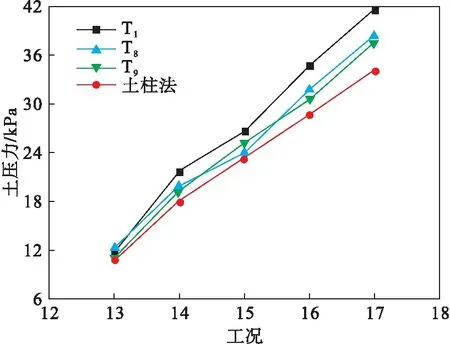
图13 管顶土压力变化规律Fig.13 Variation rules of pipe top earth pressure
3.3.2 管顶土压力系数分析
由图14可知,管涵顶土压力系数随填土高度的增加呈波动性变化,即先增加后减小,此后又随着填土高度的增加而增大,但整个填土过程中,管顶土压力系数大于1.在管顶填土初期时,由于钢波纹管涵的刚度与土的刚度差异较大,造成管顶产生不均匀沉降,进而产生应力集中现象,随填土高度不断增加,应力集中现象也逐渐加剧,导致管顶土压力系数增大;随填土的继续进行,管涵顶部产生土拱效应,减弱了应力集中现象,使管顶土压力系数减小.管涵上部填土内部所产生的土拱是不稳定的,从力学角度可看作是一种受力的传递过程,即土拱的形成—破坏—新土拱的形成.
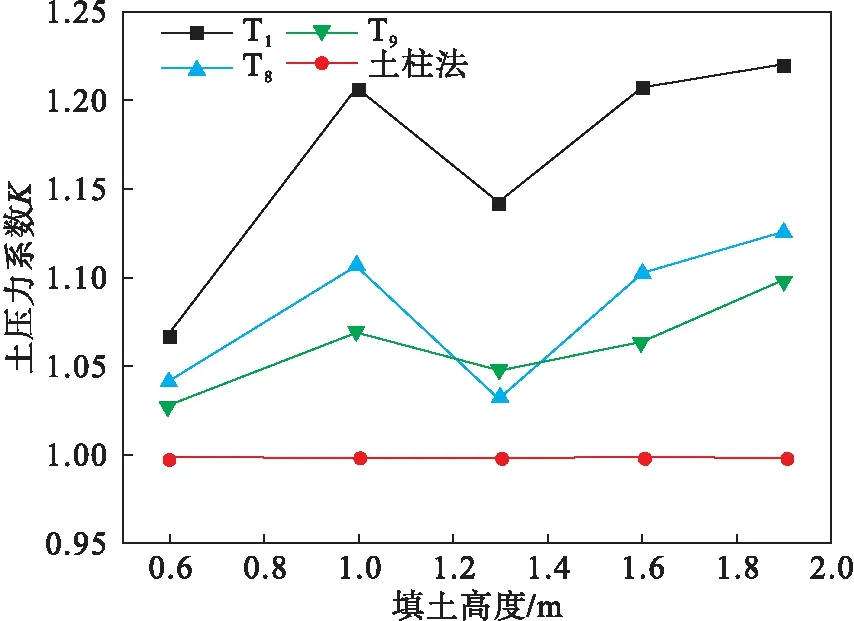
图14 填土高度对土压力系数的影响Fig.14 Effect of filling height on the earth pressure coefficient
4 梯形沟槽管顶部垂直土压力计算
在实际工程中,由于土体的抗剪强度不足,沟槽往往被挖得较深,而沟槽壁都设有特定的坡度来保证其稳定性.依据现场实际工况,对梯形沟槽垂直土压力进行了研究.
土体在外荷载和重力荷载作用下会产生沉降,竖直面和倾斜面间的土体在外荷载作用下会产生土拱效应,如图15所示.m,n两点的应力状态相同.由于倾斜墙面存在,导致小主应力面o′o发生偏转.使得o′o两侧的曲率不同,并沿倾斜面向下.计算梯形沟槽管涵顶部垂直土压力时,考虑了土拱效应影响的侧向土压力系数,其基本假设如下:1)计算模型采用平面应变问题;2)“滑动面”和“等沉面”假设与Marston理论假设一致;3)“等沉面”上部荷载为均布荷载并作用于管涵顶部;4)管涵周围填土性质各向同性;5)管涵上部和管侧的土体形成的相对运动采用极限状态表示.
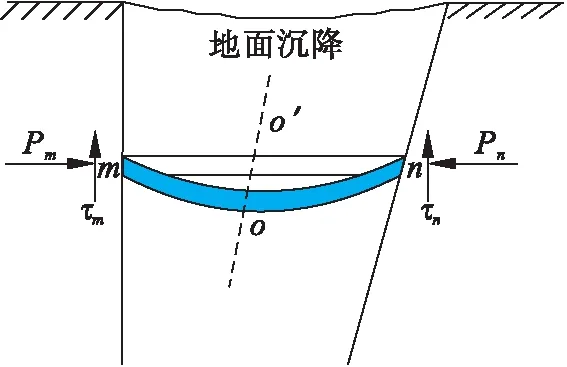
图15 竖直和倾斜墙之间拱效应Fig.15 Arch effect between the vertical and inclined walls
土体的抗剪强度为
τ=(σ+c/tanφ)tanφ.
(1)
式中:σ为正应力;φ为内摩擦角;c为黏聚力.
由式(1)可知,如需考虑土体的黏聚力,可将其转化为内部压力,计算土体抗剪强度可不考虑黏聚力的影响.
1) 当填土高度H≤he时,不存在“等沉面”(高度为he).图中b1,b2分别为单元体(厚度为dz)顶部和底部的宽度,上、下面分别为作用正应力q和q+dq,z为管侧填土距地表的深度,R为作用在单元体上的反力与夹角φ,计算模型如图16所示.
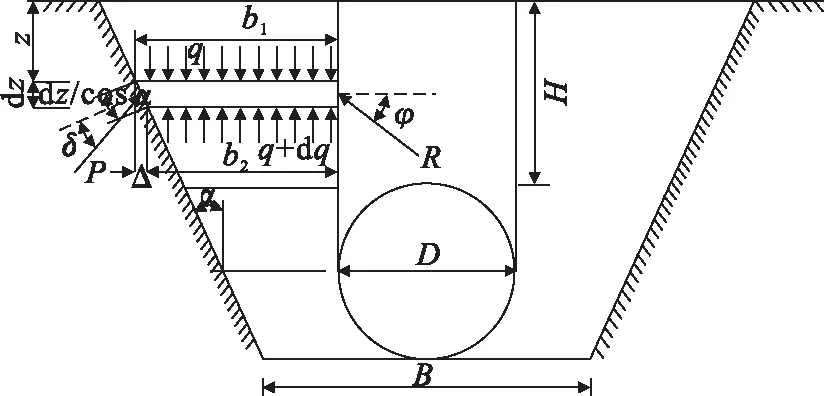
图16 当H≤he时,垂直土压力计算模型Fig.16 Calculation model of the vertical earth pressure when H≤he
由图16可得自重dG及沟槽侧壁对微单元的反力P分别为
dG=γdz[(H-z+D)tanα+0.5(B-D)] ,
(2)
(3)
式中:p′为侧壁对微单元的反力强度;B和D分别为沟槽宽度和管涵直径.
管涵上部土体对微单元的反力R为
R=(r+c/sinφ)dz.
(4)
式中,r为上部土体对微单元的反力强度.
微单元体在自重dG、正应力q和q+dq及反力P和R作用下,处于平衡状态.由∑X=0和∑Y=0可得
(5)
(6)
在水平微单元上,作用力对单元体厚度的水平中心线与管涵上部土柱以及管侧土柱接触面的交点力矩之和为0,即∑M=0,可得
(7)
令式(6)、式(7)相等并令λq=(p′+c/(tanφcosδ)),可得
λsin(α+δ)-λcos(α+δ)tanφ=sinα,
(8)
(9)
把λq=(p′+c/(tanφcosδ)代入式(6)并进一步整理可得
(10)
式中:C1为积分常数,可通过边界条件确定;A=1-λE;H1=H+D+(B-D)/2tanα;E=[sin(α+δ)+cos(α+δ)tanφ]/sinα.
当填土表面无荷载时,可确定积分常数C1:
(11)
将式(11)代入式(10),两边同乘λ得
(12)
把式(5)和λq=(p′+c/(tanφcosδ))代入式(12)可得作用在管侧土体和上部土柱之间的土压力强度r:
(13)
由式(13)可知,管侧土体与涵洞土柱之间的压力强度由土体自重产生的荷载和管涵上部无荷载时土体之间的黏聚力组成.积分式(13),可得内外土柱之间的作用力R1:
(14)
式中:γ为土的容重;φ为土的内摩擦角;α为沟槽的倾角;H为管侧填土计算高度;η为H1/H;δ为沟槽侧壁与土之间的摩擦角;E,A,λ为系数.
管顶垂直土压力为
P=DHγ+2R1sinφ.
(15)
管顶垂直土压力系数为
Kg=1+2R1sinφ/(DHγ) .
(16)
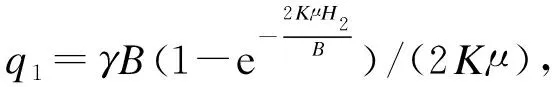
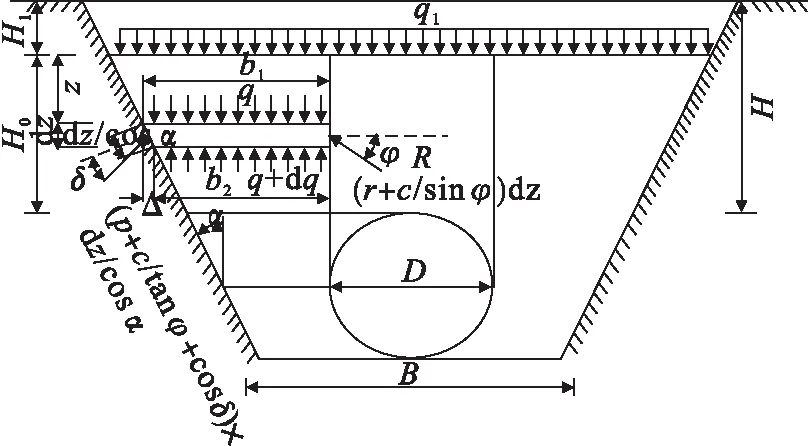
图17 当H>he时,垂直土压力计算模型Fig.17 Calculation model of the vertical earth pressure when H>he
等沉面上部土体产生的均布荷载为q1,令z=0,代入式(10)可得
(17)
式中,H2=H0+D+(B-D)/2(tanα).
可得水平微单元体上作用力q:
(18)
式(5)和式(p′+c/tanφcosδ)=λq代入式(18)可得
(19)
可知,等沉面存在情况下,管侧土体和上部土体间的土压力强度r主要由填土自重产生的土压力、黏聚力及均布荷载组成.在填土深度[0,H0]内对r积分可得管涵外侧土体与上部土体间的作用力:
(20)
式中:η为H2/H,其余符号所代表的含义与式(14)一致.
涵管顶部垂直土压力为
P=DH0γ+2R2sinφ+q1D.
(21)
管涵顶部垂直土压力系数为
(22)
由式(16)和式(22)可知管涵顶部垂直土压力系数随内摩擦角φ的增加而增加,但对土压力系数的影响却在减少.在H/D一定时,管顶垂直土压力系数随沟槽宽度的增大而增加;在B和D一定时,随H/D的增加呈先增加后减小,系数减小是由于填土达到一定高度时,会形成卸荷拱效应.
5 管涵力学性能有限元计算
5.1 三维有限元模型建立
采用ABAQUS软件建立钢波纹管涵洞有限元计算模型,忽略管涵厚度的应力变化,采用均质壳S4R单元为计算单元,土体的单元类型采用C3D8R单元,计算模型如图18所示.
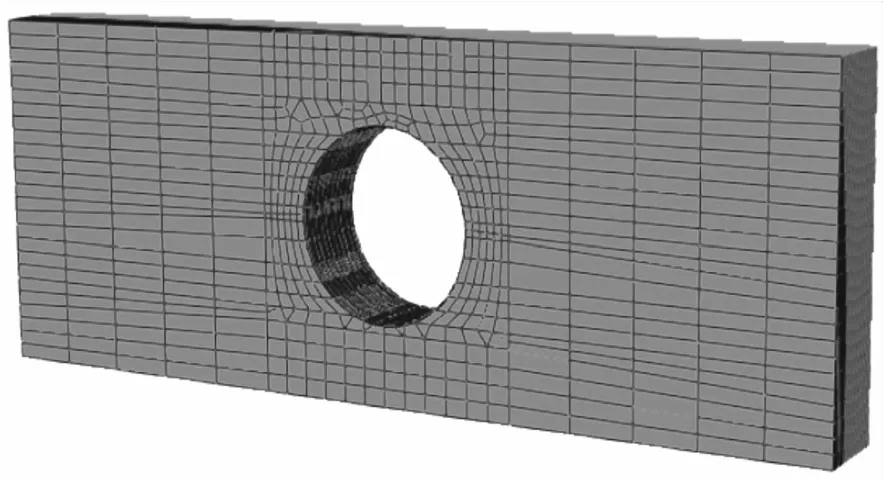
图18 钢波纹管涵有限元模型网格划分Fig.18 Mesh division of the finite element model of the steel corrugated pipe culvert
5.2 计算参数
根据现场条件,填土由掺灰量为10%的黄土组成.管涵采用Q235钢板制成,本构模型采用理想线弹性模型,但管侧填土需考虑土体的弹塑性,计算参数如表1所示.
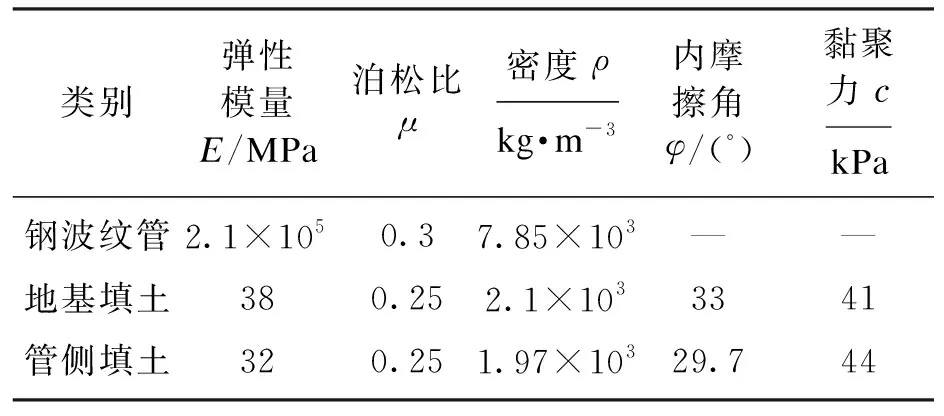
表1 钢波纹管与土体参数Table 1 Parameters of the steel corrugated pipe and soil
5.3 实测结果与有限元结果对比分析
分层填土有限元模型位移云图与钢波纹管轴向位移变化趋势如图19,20所示.
由图19可知,填土完成后,在地表处发生最大竖向位移.提取钢波纹管涵顶部的上部土层,由图21可知,管侧面填土的竖向位移大于管顶填土的竖向位移,表明周围土体对管涵顶部产生额外附加压力.实测位移与有限元计算值对比如图21所示.管顶垂直土压力对比如图22所示.
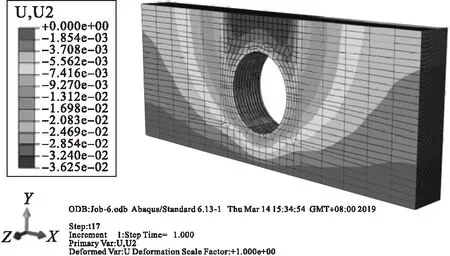
图19 填土完成后的竖向位移Fig.19 Vertical displacement after filling
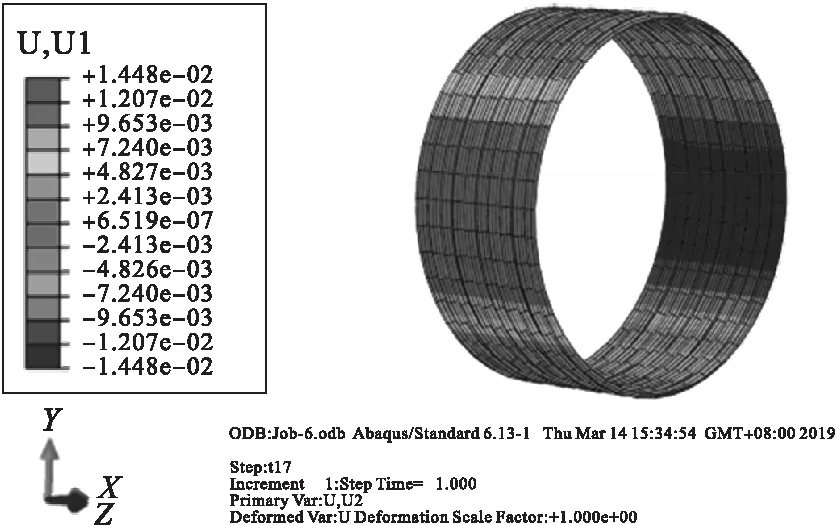
图20 管涵X轴方向的位移Fig.20 Displacement of culvert along the X axis
由图21,22可知,竖向位移和水平位移与有限元的结果有较好的一致性,与实测位移相比,差异很小.有限元计算管顶垂直土压力与土柱法的理论计算与试验值吻合较好,文献[18]的计算结果相对现场试验值偏大,但有限元法和试验测点计算的整体土压力高于用土柱法计算的土压力.由于钢波纹管涵洞与其周围填土的刚度差异较大,随填土的增加,管涵顶部平面产生不均匀沉降,在管涵顶部出现了应力集中现象.
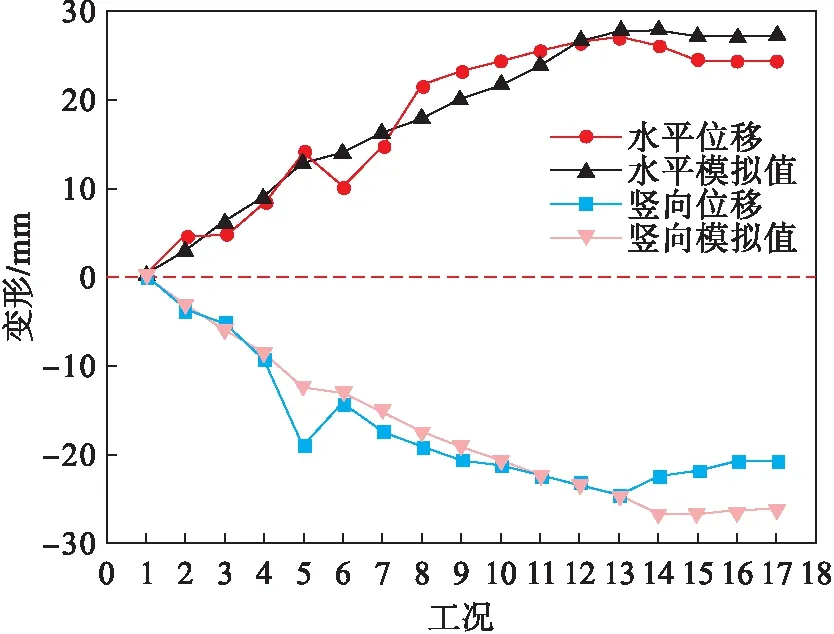
图21 水平、竖向位移对比Fig.21 Comparison of horizontal and vertical displacements
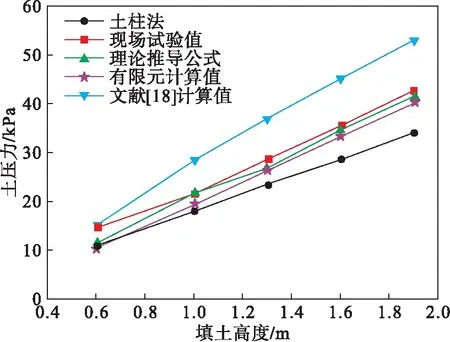
图22 管顶垂直土压力对比Fig.22 Comparison of the vertical earth pressure on the pipe top
6 结 论
1) 钢波纹管涵的应变在管顶较大,在施工过程中,要进一步对管顶做防护.管涵的水平和竖向变形分别在管侧填土过程中呈压缩和拉伸,截面的最终变形为竖向椭圆形.
2) 在钢波纹管侧及上部填土过程中,管侧填土对管涵的应变、变形及土压力分布起重要影响,而管顶一定厚度的填土对管侧填土产生的影响起减弱作用,施工时应注意管侧填土对管涵的影响.
3) 结合现场试验与理论计算,管侧填土对管涵上部产生向下拖拽力,导致管顶垂直土压力实际值大于土柱法计算值.因此,在施工设计中,应避免过高估计管涵的承载能力而导致灾害发生.
4) 针对低填方的钢波纹管涵,从常规管顶垂直土压力计算入手,采用分层分析法,推导了低填方沟埋式钢波纹管涵垂直土压力计算公式.由公式得出管顶垂直土压力系数随内摩擦角φ增大而增大,但φ的增加对管顶土压力系数的影响逐渐变小.现场试验数据及有限元模拟验证了该计算公式的可靠性.
