机器人末端复杂环境下力自适应控制
2022-09-21蒙奎全秦远田蒋祺郑铭跃朱伟
蒙奎全,秦远田,蒋祺,,郑铭跃,朱伟
(1.南京航空航天大学航天学院,江苏南京 210016;2.昆山华恒焊接股份有限公司,江苏昆山 215300)
0 前言
随着机器人应用场景不断丰富,机器人与环境的交互也越来越频繁。诸如使用医疗机器人进行辅助手术,焊接行业中应用较广的摩擦搅拌焊接技术,机加工行业中的打磨抛光等,都需要对机械臂末端进行力的精确控制。由HOGAN提出的定参数阻抗策略可以对机器人进行末端力控制,但是其各阻抗参数均为定值,在环境刚度变化和未知位置情况下,无法准确地跟踪到期望力。为了解决环境自适应问题,SERAJI提出了一种基于模型参考的自适应阻抗控制理论,该理论运用Lyapunov稳定性理论设计MARC控制系统,使得控制误差力跟随误差参考模型,从而实现实际力与期望力在复杂环境下的动态跟随。随后LIN等研究了此方法在机械臂柔顺法兰抛光下的自适应力控制,能够较好地跟踪到期望力,但是稳态误差较为明显。邢宏军等研究了模型参考自适应阻抗控制机器人开关阀门,解决了阀门开关过程中的力控制问题,并能够精确地控制阀门的开度。LV等研究了用于下肢康复机器人的自适应阻抗控制,实验结果表明该方法可将控制力误差控制在2.5 N内。BONILLA等基于机器人逆动力学的PD闭环控制提出一种新的自适应阻抗控制策略,该方法能够同时实现在自由空间和受限空间内的跟踪控制。JUNG和HSIA针对复杂环境的力自适应控制提出一种控制算法,通过补偿阻尼参数达到复杂环境下力的自适应,该算法十分简洁,易于编程实现,并且追踪效果很好。CAO等针对两连杆机器人的末端外力控制,采用该自适应算法得到了准确的力跟踪曲线,给出了该控制算法的误差离散形式。甘亚辉等、DUAN等研究了单臂机器人在平面、弧面和孔洞环境下力自适应控制,得到了较好的力跟踪效果。武琦琦研究了基于力矩控制模式下的机器人力自适应控制算法,通过Delta机器人实验准确跟踪到了期望力。甘亚辉等基于闭链系统力/力矩分配原理,研究了双臂机器人协同下的力自适应控制,提出了一种双臂对等式的力自适应控制结构。此外,将阻抗控制与智能算法相结合:LI等在定阻抗参数的基础上通过遗传算法进行参数寻优,研究了双臂机器人变参数阻抗控制;QU等针对外骨骼机器人力控制研究了基于模糊控制的阻抗控制。
本文作者在自适应力控制的基础上,提出了一种机器人复杂环境交互的力控制策略,研究了机器人在变刚度和变位置条件下对恒力、正弦力和斜坡力的跟踪效果。针对双臂机器人协同内力控制,提出了一种从臂变参数阻抗控制策略,该方法能够解决双臂协同的内力问题。
1 自适应阻抗控制数学模型
传统的阻抗控制将机器人末端与外界环境接触等效为二阶动力学模型,如图1所示。
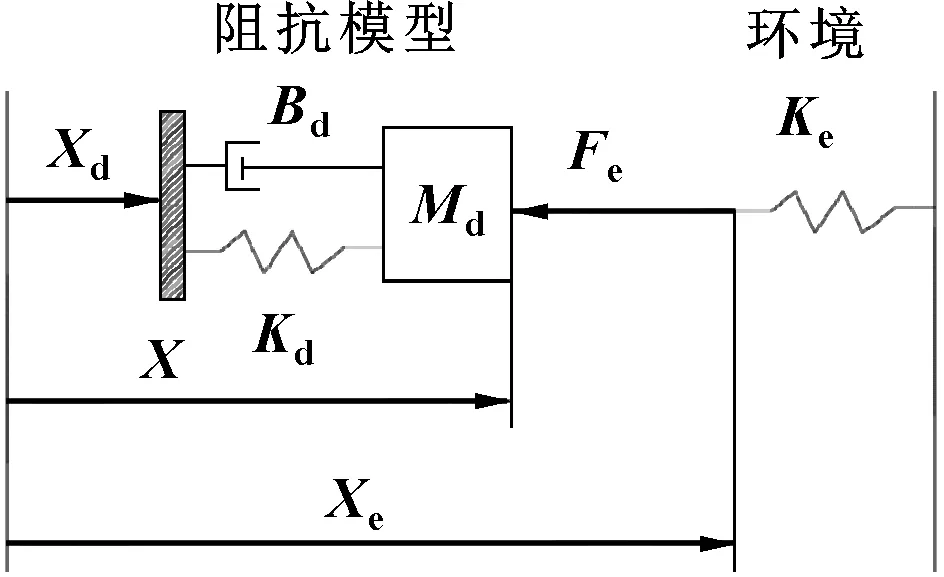
图1 阻抗控制模型
阻抗控制的数学模型:

(1)
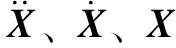
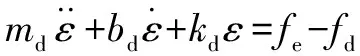
(2)
在FS(Free Space)空间下,接触力为0
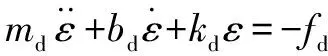
(3)
将期望力设置为0时,给出确定的运动轨迹,此时机器人处于完全的位置控制模式下。当机器人末端与环境接触,即处于CS(Contact Space)空间下,接触力=(-),阻抗公式表示为
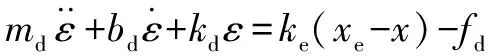
(4)
为保证稳态下力能够稳定跟踪,使=0
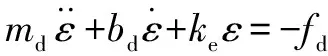
(5)
分析上式可知:当稳态下即使环境刚度未知,但总存在合适的使得等式成立。实际中,环境位置并不总能精确地得到,对力的跟踪效果产生较大的影响。假设位置误差为δ,则′=+δ,同理′=+δ。
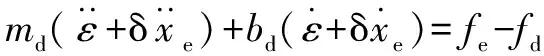
(6)


(7)
δ为补偿时变函数
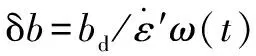
(8)
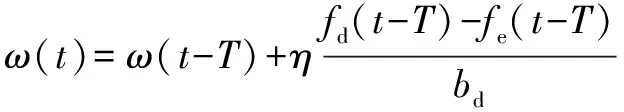
(9)
其中:为力误差的动态更新率;为力传感器的采样时间间隔。核心思路是通过上一时刻的期望力与反馈力的误差来实时修正阻抗参数模型,达到自适应的目的。
为了便于编程控制,给出该方法的离散形式:
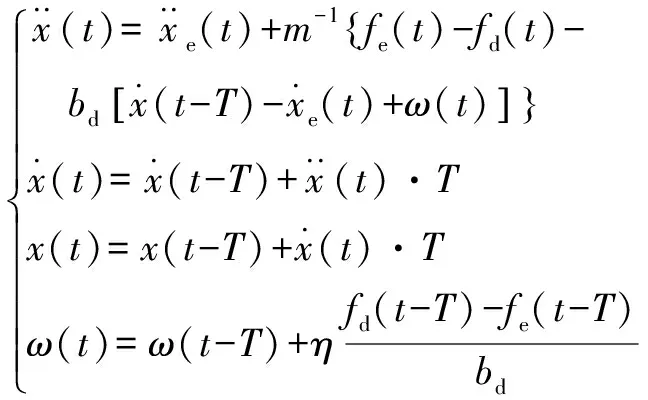
(10)
最后()送入机器人控制系统进行控制。
以上为机器人单自由度的形式,空间刚体运动存在6个自由度(),如图2所示。
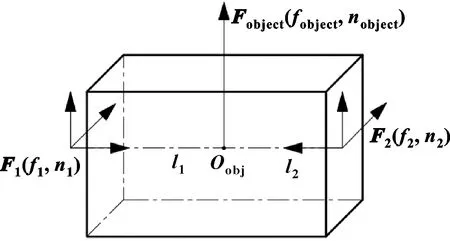
图2 夹取物体受力
其中(,)(=1,2)为六维力向量,3个方向的力矢量和力矩矢量。1为主机械臂,2为从机械臂,为质心点,、为接触点到质心的距离,(,)为驱动物体运动的六维力矢量。
为了研究目标物体与末端执行器之间的运动,以机器人的末端TTE坐标系为参考。机器人末端的TTE坐标系为将6轴的D-H系平移得到,所以目标物体的内力通过末端坐标系的方向得到,控制方程如式(10)所示,此称为内力阻抗。
双臂夹取物体朝末端坐标系的、和方向运动时符合牛顿第二律=,此时通过外力阻抗进行控制。若物体运动产生方向的加速度,则需要同时产生方向上的夹紧力和加速度的合力,如图3所示。

图3 z运动方向受力
其中1为主臂受力,2为从臂受力。此时主臂仅提供目标物体期望的内力,从臂需要提供目标物体期望的内力加方向运动的驱动力。沿和方向的加速运动由摩擦力提供,摩擦力与方向的正压力相关,所以和方向上的运动关系与方向上的夹紧力存在耦合。因此刚体平移下的阻抗控制如下:
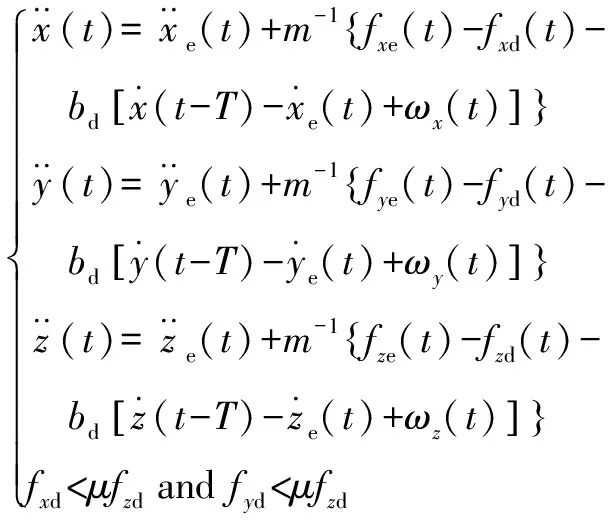
(11)
其中:e代表反馈力;d代表期望力;=,,;为接触盘与物体间的摩擦因数。
当双臂机器人操纵刚体在空间中转动时,由质心旋转力矩=可知机器人末端需要提供期望的力矩。用、、代表刚体转动的欧拉角,该欧拉角定义与机器人末端姿态定义相同,姿态控制阻抗方程如式(12)所示。其中e为反馈力矩,d为期望力矩,=,,。
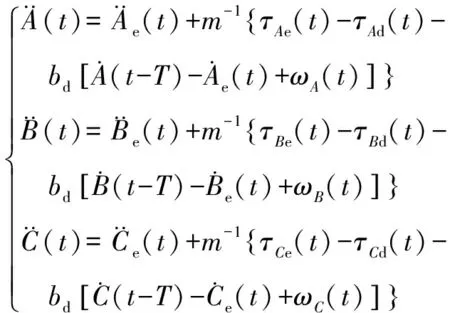
(12)
结合式(10)—(12),得到双臂机器人夹取空间刚体六自由度运动的内外力阻抗控制方程。
2 自适应阻抗控制稳定性证明
式(7)给出了自适应阻抗控制的数学形式,下面将对该控制模型进行稳定性证明。对式(7)进行拉普拉斯变换得
(+)()+()=-Δ()-()
(13)
其中:Δ()=()-(),()=(+)·δ()。对()进行拉普拉斯变换,根据延时平移定理可得:
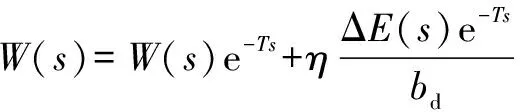
(14)
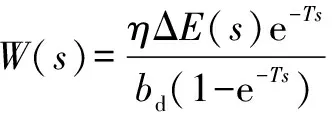
(15)
由泰勒展近似开式可知e-≈1-,上式变为
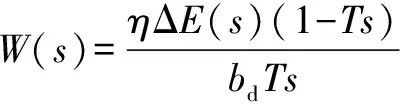
(16)
上式代入阻抗公式得:
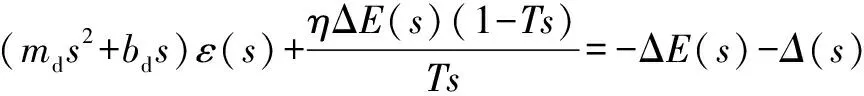
(17)
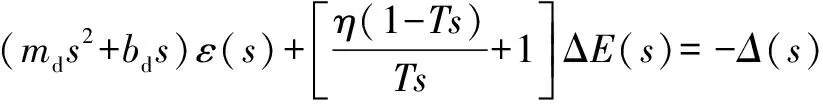
(18)
注意到外部力的计算可以等价为一阶线性弹簧的计算:
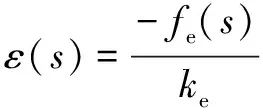
(19)
代入式(18):
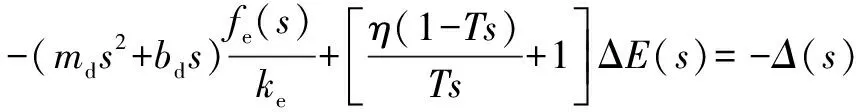
(20)
进一步化简
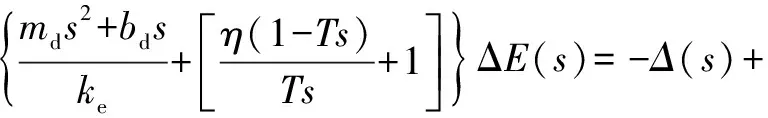
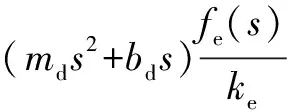
(21)
上式右边可以看作扰动输入函数,则左边可以转化为
++(1-)+=0
(22)
对上特征方程进行稳定性分析。通过劳斯判据可知:如果特征多项式稳定,就必须使得所构成的三阶系统劳斯表的第一列元素全部大于零并且多项式的系数全部大于零。劳斯表如下所示:

满足第一列所有元素大于零
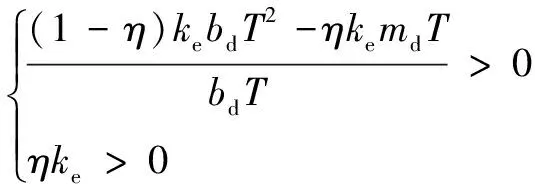
(23)
满足所有系数大于零
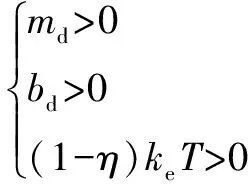
(24)
求上述约束条件的交集可得
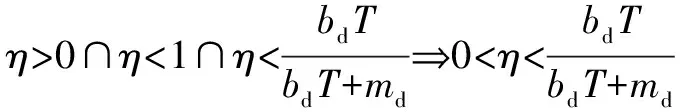
(25)
可以看出系统的稳定性仅仅取决于力误差的动态更新率、阻抗惯性参数、阻抗阻尼系数。
3 单/双臂机器人控制仿真平台
3.1 单臂搅拌摩擦焊机器人力控制
以单臂机器人执行搅拌摩擦焊为例,末端接触焊接平台上的工件,因而实际只承受单方向的力。则末端六维力控制可以等效为垂直于接触面的单自由度力控制。通过SolidWorks建模后导入ADAMS中的模型如图4所示。
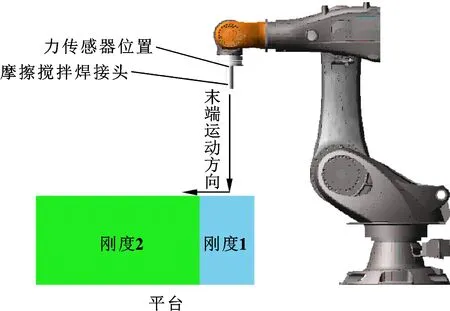
图4 单臂ADAMS仿真模型
机器人末端先垂直向下运动,在未与平台接触前为自由空间运动,此时机器人为纯位置控制模式。在与平台接触的瞬时变为接触空间运动,此时需要通过自适应模块根据接触环境的刚度和位置变化实时调整接触面法向位置。控制框图如图5所示,在控制方向上通过自适应控制模块进行实时调整。在非控制方向上,通过纯位置直接控制。Simulink控制程序如图6所示。

图5 单臂机器人摩擦搅拌焊阻抗控制
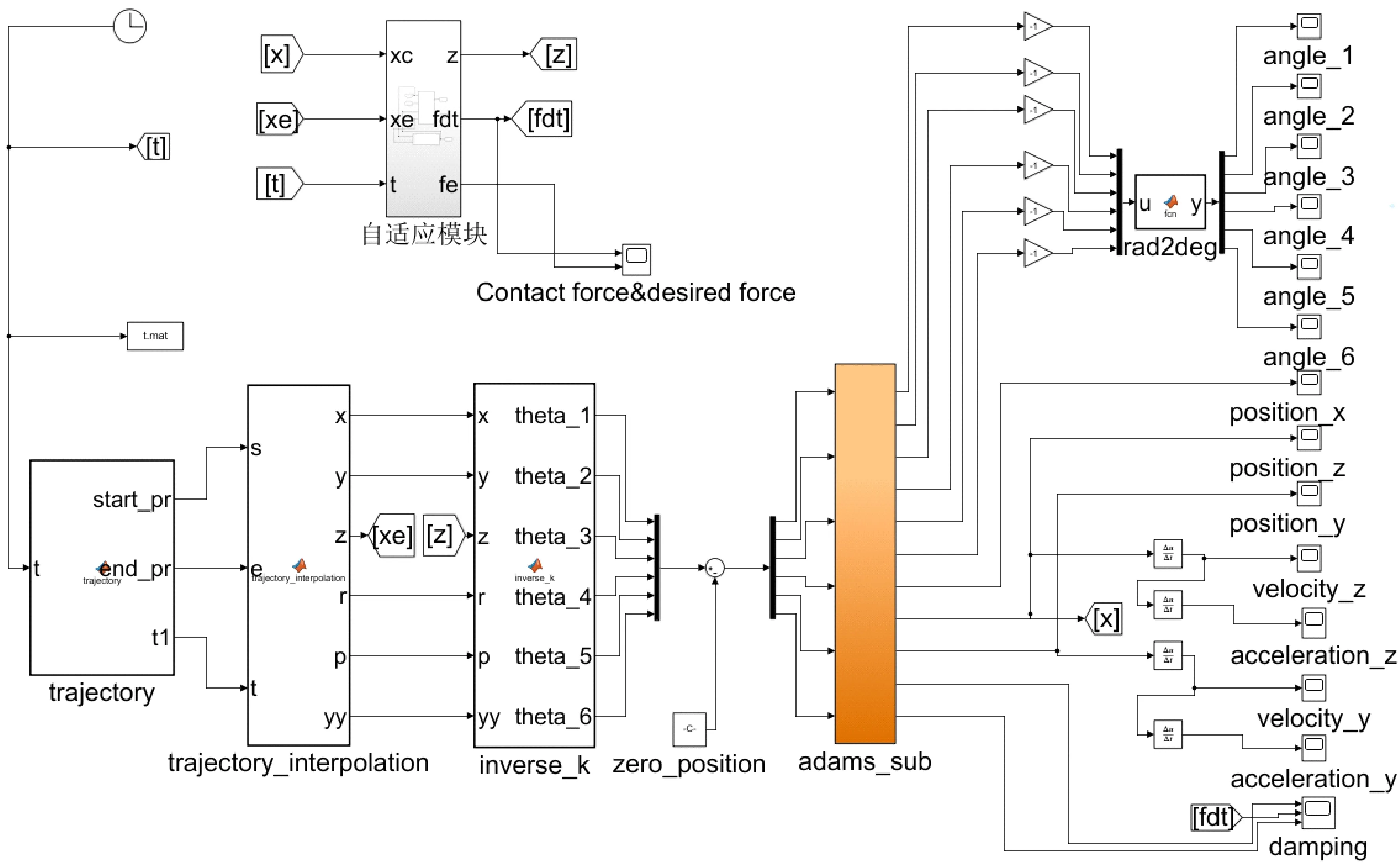
图6 单臂机器人摩擦搅拌焊Simulink与ADAMS联合控制仿真
3.2 双臂机器人协作力控制
文中在单臂自适应力的基础上,提出基于该方法的双臂机器人主从控制策略。以双臂夹取物体为例,其中主臂按照规划的轨迹运动,从臂通过自适应模块跟踪主臂的轨迹,实现自适应控制。ADAMS模型如图7所示。
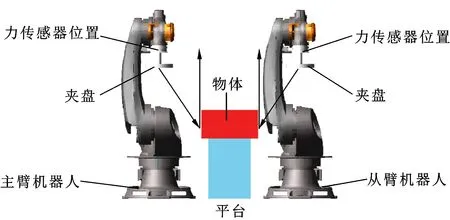
图7 双臂ADAMS仿真模型
双臂机器人首先向下运动接触目标物体。在接触目标物体后,主臂向上运动,从臂通过自适应模块控制目标物体内力跟随主臂运动,从而实现双臂协作力控制。通过双臂控制目标物体的内力,实现目标物体的夹紧力,理论上在摩擦力的作用下将目标物体举起,跟随双臂机器人一同运动。控制框图如图8所示,Simulink控制程序如图9所示。

图8 双臂机器人主从协作控制
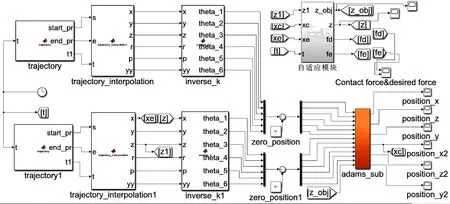
图9 双臂机器人主从协作Simulink与ADAMS联合控制仿真
3.3 自适应阻抗控制模块
单/双臂机器人自适应阻抗控制封装模块如图10所示,其中刚度变化模块设置不同时刻的接触刚度。由于ADAMS为刚体运动仿真软件,无法得出弹性体变形受力,所以在自适应控制模块里添加了刚体变形受力模块。将机器人末端与物体之间的接触力简单地等效为线性弹簧系统,如式(26)所示
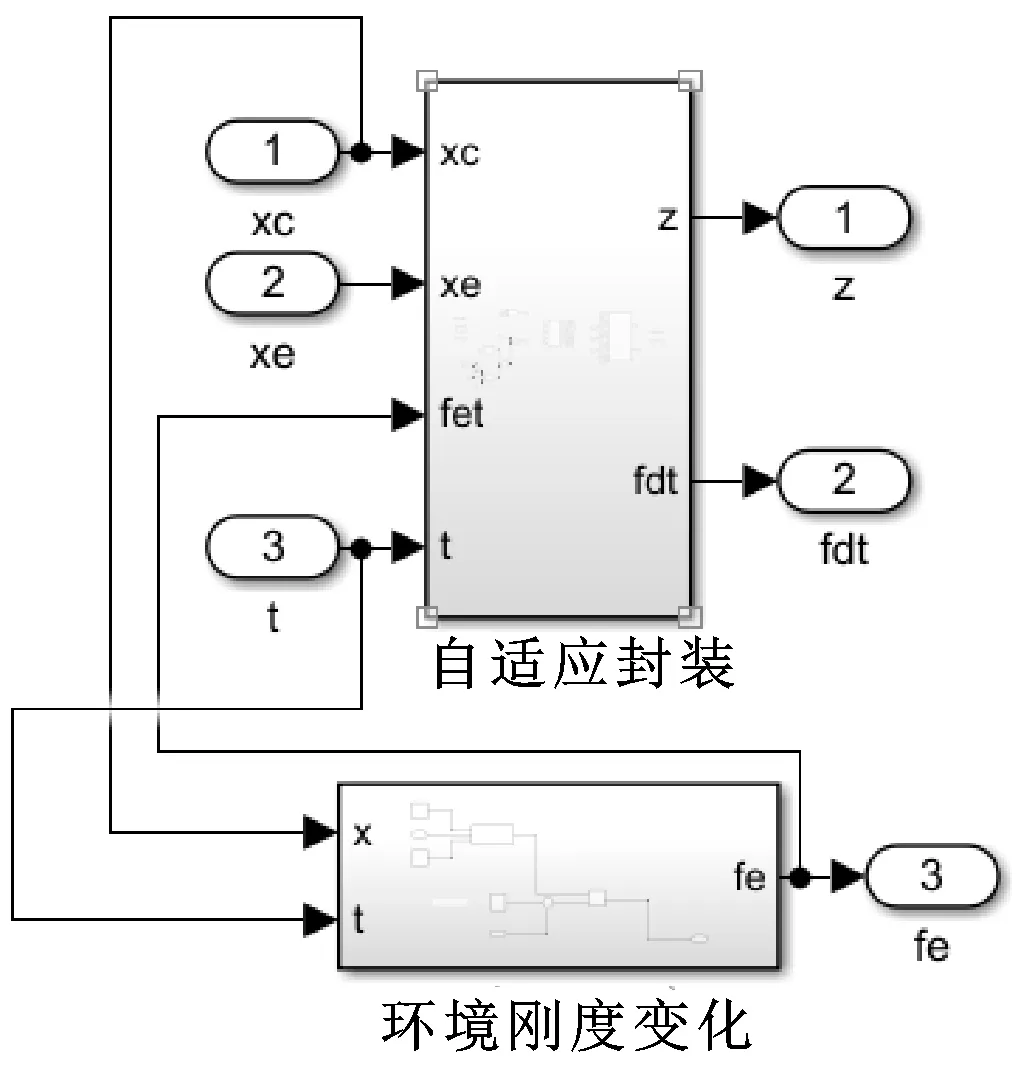
图10 自适应模块
=Δ
(26)
其中:为机器人末端力传感器的测量值;为环境刚度;Δ为环境变形量。
4 仿真结果
4.1 单臂机器人搅拌摩擦焊自适应力控制仿真
机器人末端的运动速度为0.1 m/s,运动加速度0.1 m/s,运动减速度0.1 m/s,沿接触面运动距离1 m。自适应模块动态更新率=0.05,阻抗惯性参数=1,阻抗阻尼系数=80,Simulink与ADAMS的通信周期=0.005 s。下面给出3种工况条件,单臂机器人运动,如图11所示。
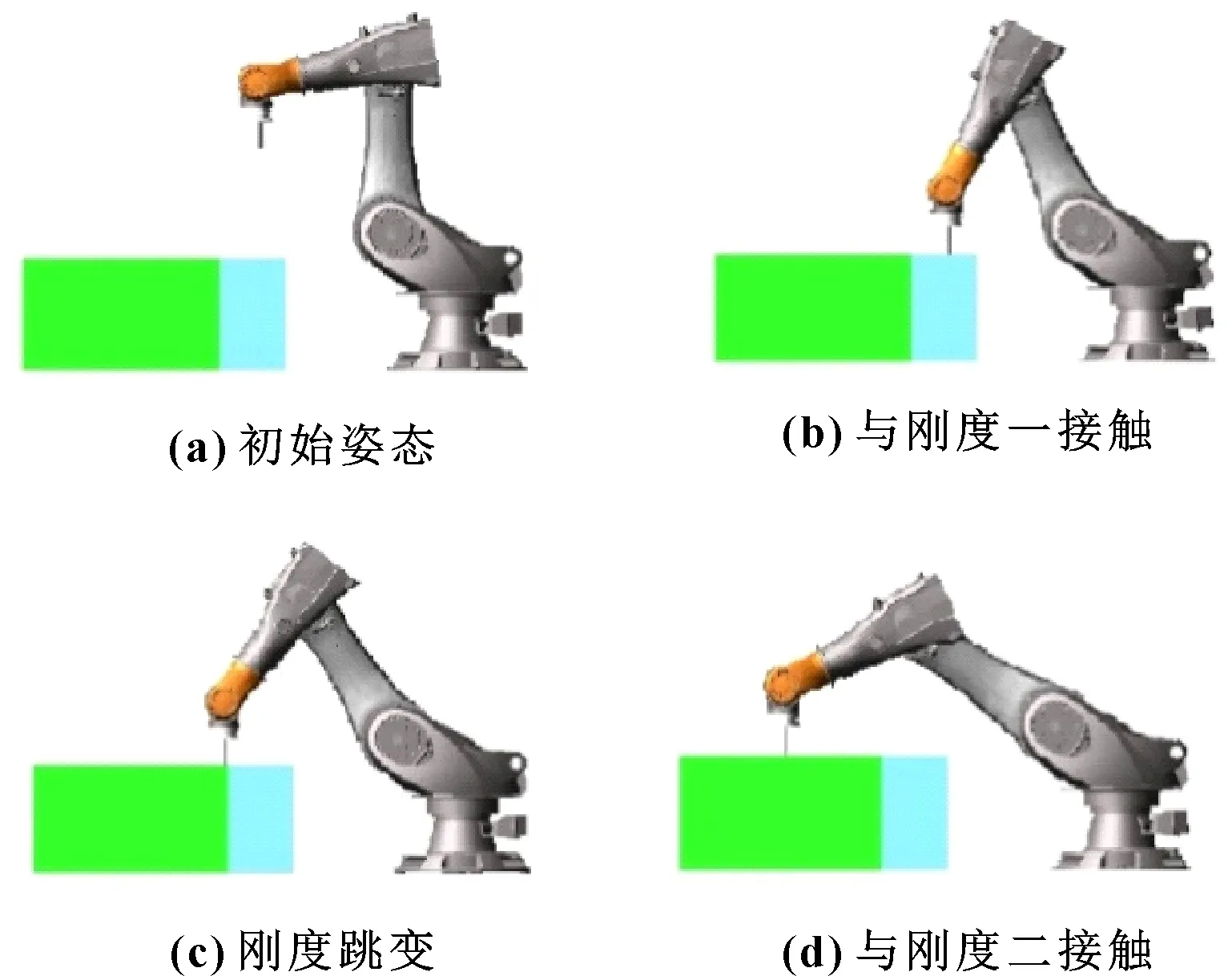
图11 单臂机器人运动
工况一:期望恒定力20 N,初始接触刚度5 000 N/m,3.5 s后接触刚度跳变到1 000 N/m。力追踪仿真结果如图12所示,弹性体的位移下压量如图13所示。
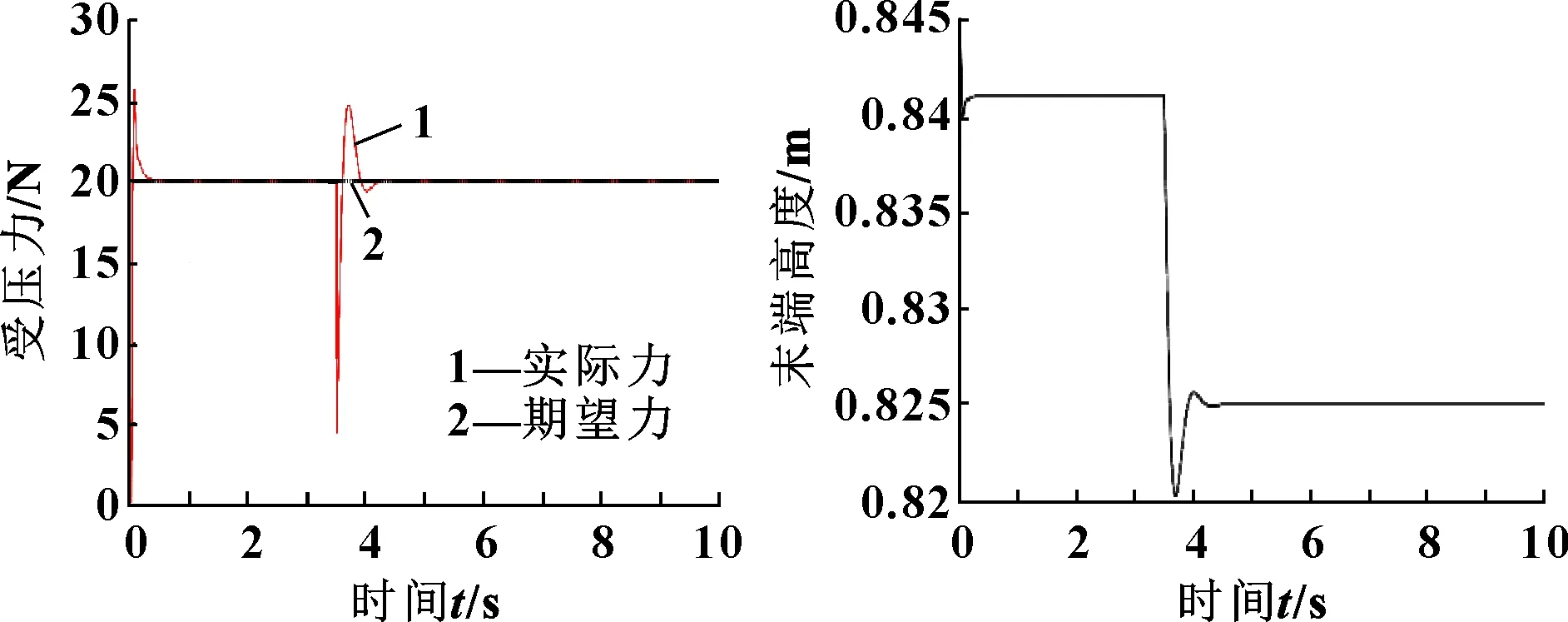
图12 定力追踪 图13 恒力下压量
工况二:期望斜坡力=2,初始接触刚度5 000 N/m,3.5 s后接触刚度跳变到1 000 N/m。力追踪仿真结果如图14所示,弹性体的位移下压量如图15所示。

图14 斜坡力追踪 图15 斜坡力下压量
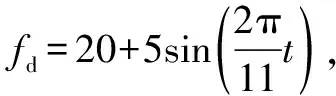
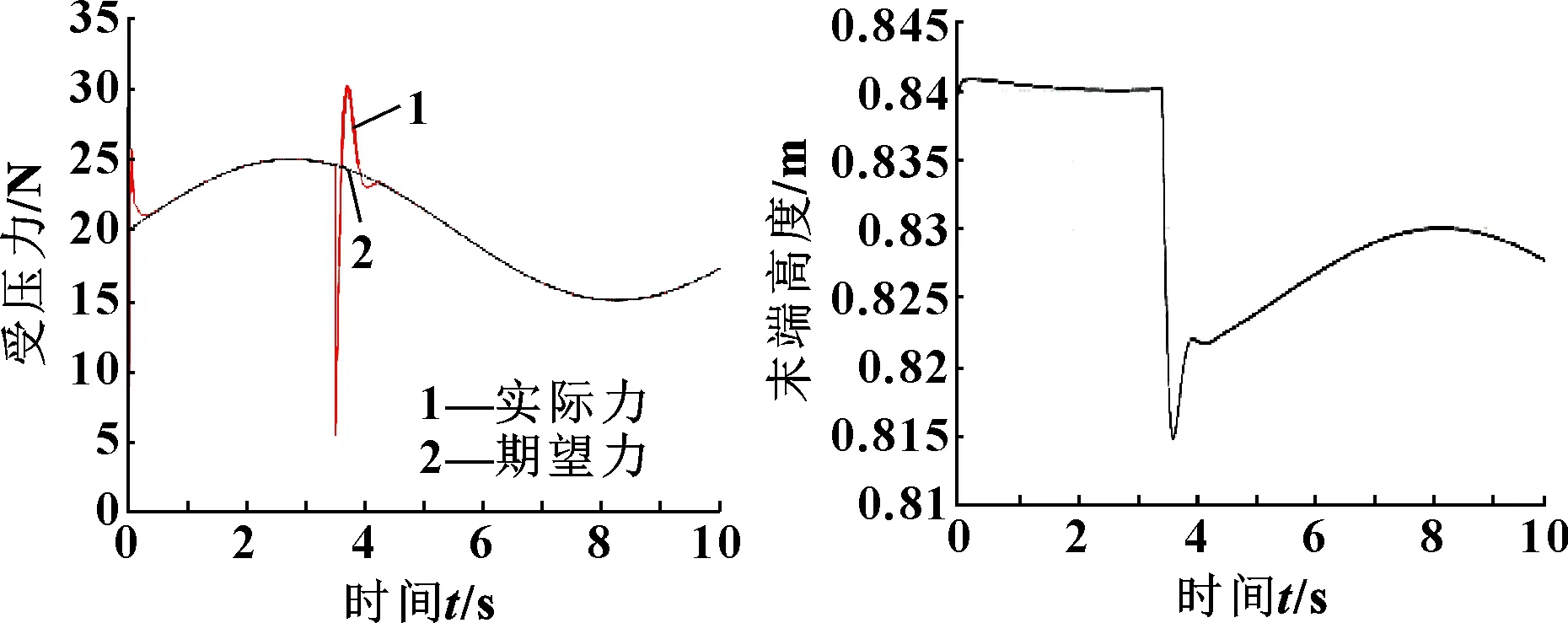
图16 正弦力追踪 图17 正弦力下压量
从图12—图17可以看出:在变力、变刚度和变位置条件下,机器人末端均能良好地跟踪到期望力。机器人末端的下压量由于刚度跳变产生的下压量变化符合弹性体不同刚度的压缩量。在=0 s初始状态,机器人末端与环境接触,产生非线性的碰撞。接触力瞬时升高,随后经过自适应模块的控制,在=0.4 s的时间内追踪到期望力。在=3.5 s时,接触末端由强刚度向弱刚度跳变,接触力会向下跳变,随后追踪到期望值。在=0 s初始状态,机器人末端产生一个下压量,在=3.5 s后由于环境变化出现刚度跳变,下压量随之产生变化。
4.2 双臂机器人物体夹取自适应内力控制仿真
双臂机器人主从臂末端的运动速度均为0.1 m/s,运动加速度0.1 m/s,运动减速度0.1 m/s,物体提升高度0.8 m。自适应模块动态更新率=0.05,阻抗惯性参数=1,阻抗阻尼系数=80,Simulink与ADAMS的通信周期=0.005 s。双臂机器人的运动如图18所示。4种目标物体刚度不同,分别为500、1 000、2 000和5 000 N/m,目标物体期望的夹取内力均为50 N,目标物体尺寸为0.8 m×0.2 m×0.4 m。物体内力跟踪如图19所示,从臂末端相对于主臂之间的压缩量如图20所示。
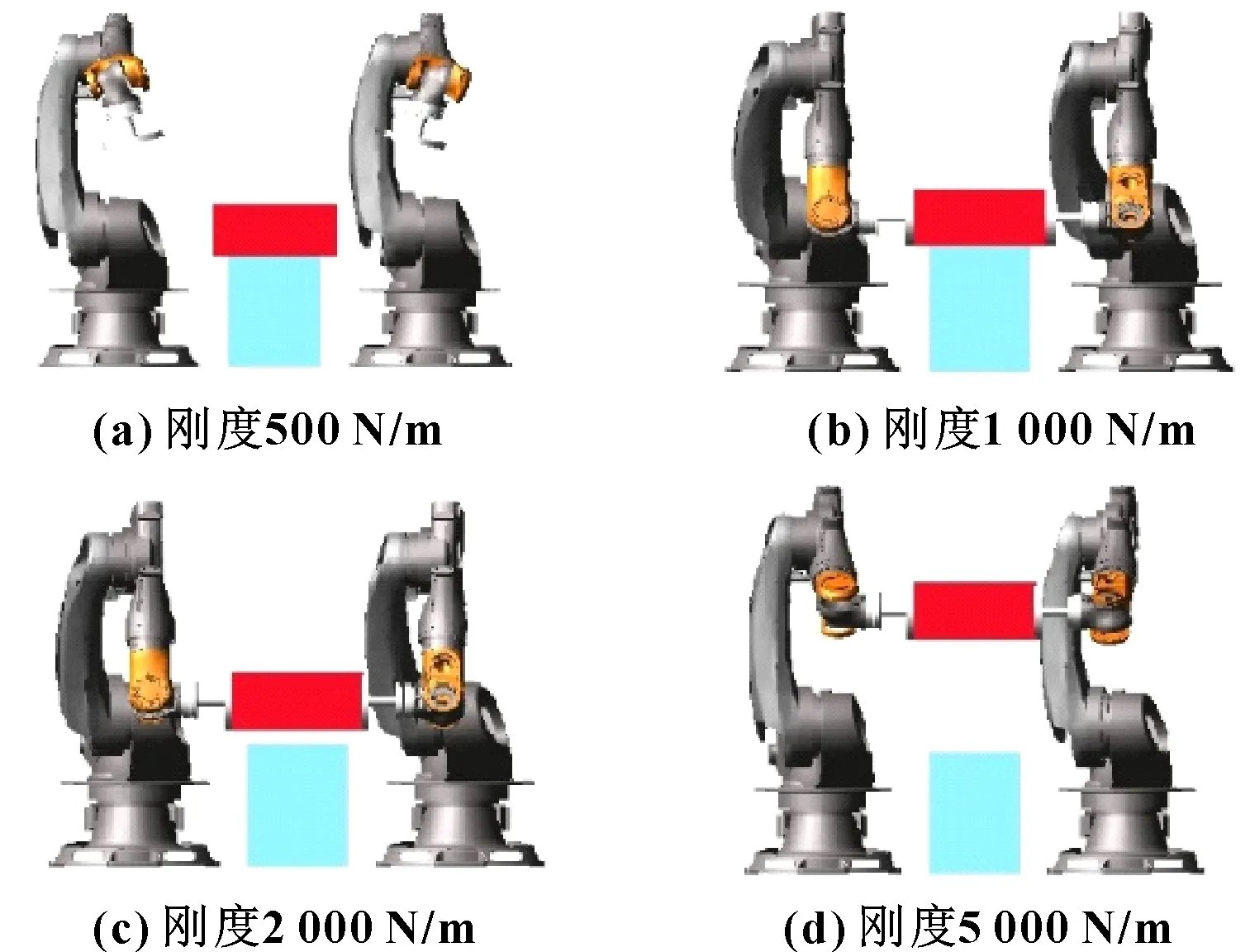
图18 双臂夹取物体运动
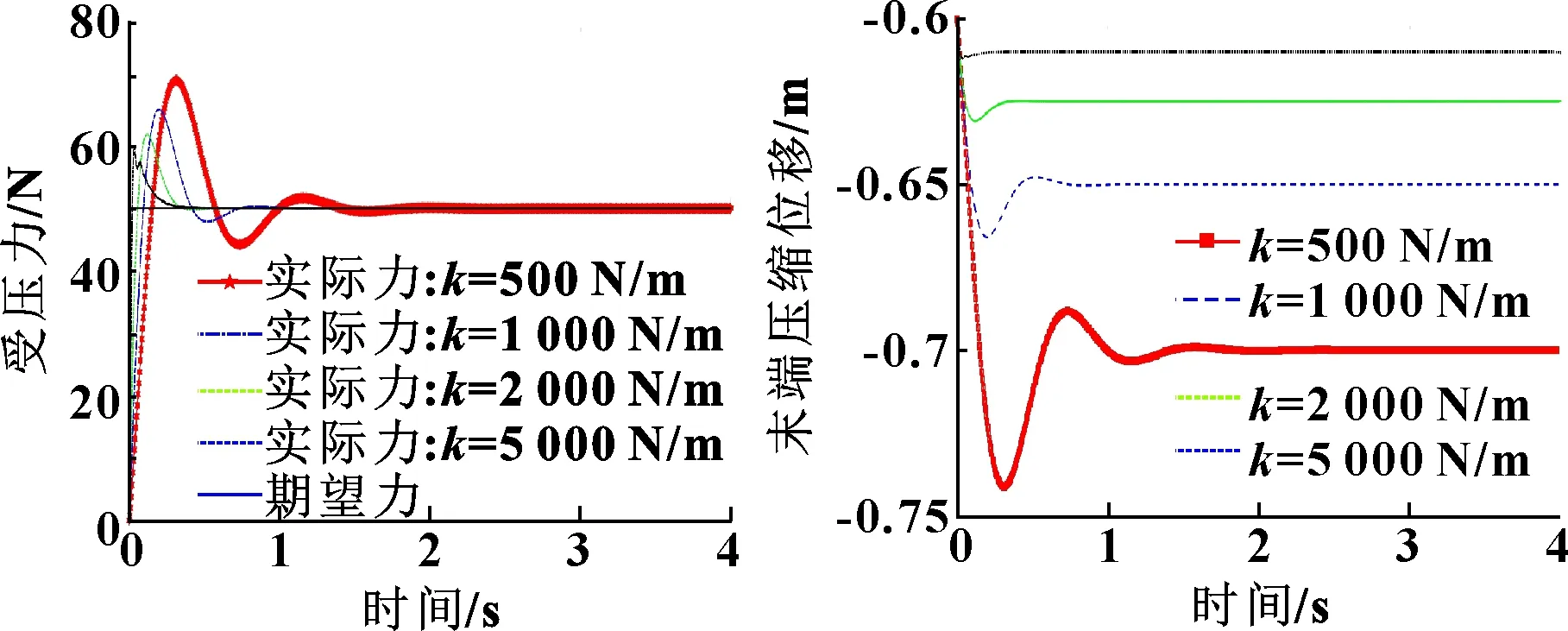
图19 目标物体的内力追踪 图20 从臂相对于主臂的位置
仿真结果表明:不同刚度的物体在双臂夹取下均能很好地控制其内力。在大刚度下,末端变化的幅度小,力追踪的速度快。在小刚度下,机器人末端运动幅度大,所用的追踪时间长。通过调整自适应更新律可以缩短调节时间,但同时容易发生震荡。
5 结论
针对机器人与复杂环境的力交互控制,提出的自适应控制策略能够很好地实现末端的期望力跟踪,同时根据末端的下压量进一步证明末端自适应阻抗控制的正确。文中给出了清晰的自适应控制方程,便于相关领域内的学者进一步研究。同时针对搅拌摩擦焊和双臂目标物体夹取,提出了单臂机器人力自适应控制环路和双臂主从控制模式的机器人力自适应控制环路。
