基于ANSYS的某型汽车起重机主臂强度分析
2016-04-26张燕燕朱明明周友坤
张燕燕,朱明明,周友坤
(1. 黄河科技学院 工学院,河南 郑州 450063; 2.河南出入境检验检疫局,河南 郑州 450003;
3.三一重工股份有限公司,湖南 长沙 430100)
基于ANSYS的某型汽车起重机主臂强度分析
张燕燕1,朱明明2,周友坤3
(1. 黄河科技学院 工学院,河南 郑州 450063; 2.河南出入境检验检疫局,河南 郑州 450003;
3.三一重工股份有限公司,湖南 长沙 430100)
摘要:以某型汽车起重机吊臂为研究对象,对其进行了理论强度分析,并利用有限元软件ANSYS,建立了汽车起重机吊臂的有限元模型,分析了在最大力矩作用下,吊臂上的应力分布情况,并将有限元分析结果与实测值进行了比较,结果表明:有限元计算结果与实测结果的最大应力发生位置相一致,且有限元分析的数值与实测值误差合理,基于ANSYS有限元软件分析的结果是可靠的。
关键词:汽车起重机;主臂;有限元;强度计算;试验
1引言
吊臂是汽车起重机上最重要的工作部件,吊臂的力学性能直接影响着起重机的起重性能和整机性能,因此对汽车起重机的吊臂进行力学分析有着重要的意义。
近年来,研究者们致力于各种汽车起重机吊臂力学性能的研究,并取得一定的成果。2003年,纪爱敏等对QY25K型汽车起重机吊臂结构进行了有限元分析,运用节点自由度耦合技术模拟各节臂的连接,所得结果与实测值较吻合,为吊臂的设计提供了有价值的参考[1];2011年,西北工业大学的韦仕富、王三民等人对某型汽车起重机吊臂进行各种工况下的有限元分析及试验验证,研究结果显示:有限元方法应用于起重机吊臂分析是可行的[2-3]。
为了进一步验证有限元法应用于汽车起重机主臂分析的可行性和可靠性,指导不易做实验研究的汽车起重机多节吊臂的强度分析、降低实验成本,笔者以国内某型号六节臂大型汽车起重机主臂为研究对象,首先用理论方法分析出各节臂上的危险截面,并计算出各危险截面上的最大应力,理论计算结果证明主臂的强度是安全的;其次,利用有限元分析软件ANSYS,以相同型号的起重机主臂为研究对象,将相邻两节臂搭接处滑块材料的非线性特征考虑进去,建立起重机主臂的有限元模型,分析了最大其中力矩作用下主臂应力的分布,并将有限元分析结果与主臂的实测试验结果做了比较,结果表明:起重机在最大起重力矩的作用下,有限元分析结果与实验结果较吻合,且都小于主臂材料的许用应力。
2理论计算
某型号汽车起重机整机结构如图1所示,该机采用六节伸缩式吊臂,各节臂之间有相对滑动,靠搭接处的支撑滑块来支撑吊臂并传力,吊臂截面采用U型+直线+弧线形式,截面形状如图2所示,工作时,U型在下,弧线形在上。

1.变副液压缸;2.基本臂;3.二级臂;4.三级臂;5.四级臂;6.五级臂;7.六级臂;8.转台支撑;9.转台;10.支腿;11.后滑块;12.前滑块图1 汽车起重机整机示意图

图2 主臂截面形状简图
主臂材料采用高强度钢板WELDOX,该材料的屈服极限为960 MPa,强度极限为980 MPa,许用应力为614 MPa。
现以吊臂全伸50 m,幅度24 m,起重量5.1 t,仰角58.8 °时的工况作为计算工况,图3上的A-A、B-B、C-C、D-D、E-E截面分别为基本臂上危险截面、二三节臂搭接处危险截面、三四节臂搭接处危险截面、四五节臂搭接处危险截面、五六节臂搭接处危险截面的位置;轴向力由伸缩油缸承受,主臂结构只承受双向弯曲。
理论计算参考文献[3],计算过程为:计算吊臂变副平面内和旋转平面内的强度计算载荷;计算吊臂变副平面内和旋转平面内的临界力;计算各个臂节搭接处危险截面的弯矩;计算两节臂搭接处危险截面的正应力;校核各个危险截面弯曲强度。计算结果如表1所示。
表1各个臂节搭接处危险截面的理论应力强度
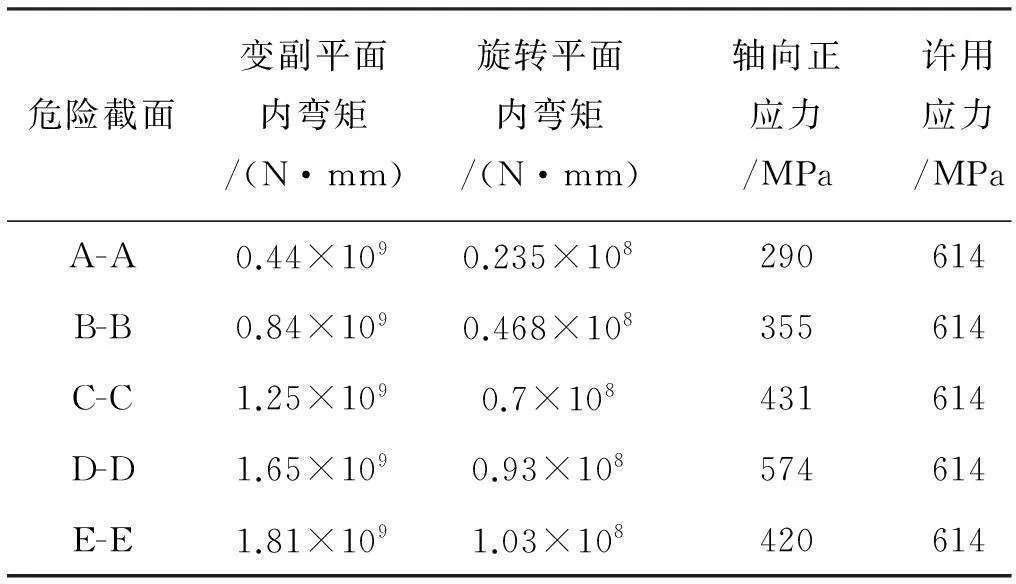
危险截面变副平面内弯矩/(N·mm)旋转平面内弯矩/(N·mm)轴向正应力/MPa许用应力/MPaA-A0.44×1090.235×108290614B-B0.84×1090.468×108355614C-C1.25×1090.7×108431614D-D1.65×1090.93×108574614E-E1.81×1091.03×108420614

图3 各个臂节危险截面位置
理论计算的结果显示,各节臂搭接处危险截面上的应力最大值为574 MPa,发生在四五节臂的搭接处,最大压力值小于臂架材料的许用应力614 MPa,说明此汽车起重机主臂强度符合要求,理论计算的结果为后面的实验验证和有限元法验证提供基础。
3有限元分析
3.1有限元模型的建立及约束条件的施加
起重机主臂由钢板焊接而成,在建立有限元模型时遵循:各板件厚度方向的位置以板厚中分面位置来确定;为保证焊接工艺而设计的板边缘对计算结果影响很小,建立有限元模型时不予考虑[4-5];在两相连臂节间滑块处建立耦合模拟臂节间连接。用自由网格划分法划分后吊臂模型的节点数为194 770,单元数196 026个。
建立约束条件时:将两相邻臂节的上部滑块连接处相对应的节点建立UX、UY两个方向的位移耦合,下部滑块连接处相对应的节点建立UX、UY、UZ三个方向的位移耦合;在臂架根部销轴连接处和臂架下侧变幅油缸销轴连接处建立刚性节点,在刚性节点上施加UX、UY、UZ、RY、RZ方向的位移约束,放开绕X轴旋转方向的RX方向位移约束。
施加载荷时,选取的计算工况与理论分析时的工况一致[6-8],在最大力矩的作用下分析主臂的受力情况。
3.2有限元分析结果
在最大力矩的作用下,主臂的整体应力分布如图4所示,基本臂的应力分布如图5所示,其余各节臂搭接处的应力分布如图6—图9所示,从图5—9中能清楚的看到,主臂的最大应力发生在基本臂上的变幅油缸铰耳根部前端处,在图5中M点的位置,应力大小为415 MPa左右,小于材料的许用应力614 MPa。耦合区的应力集中与模型的简化有关,不可避免,故不作说明。
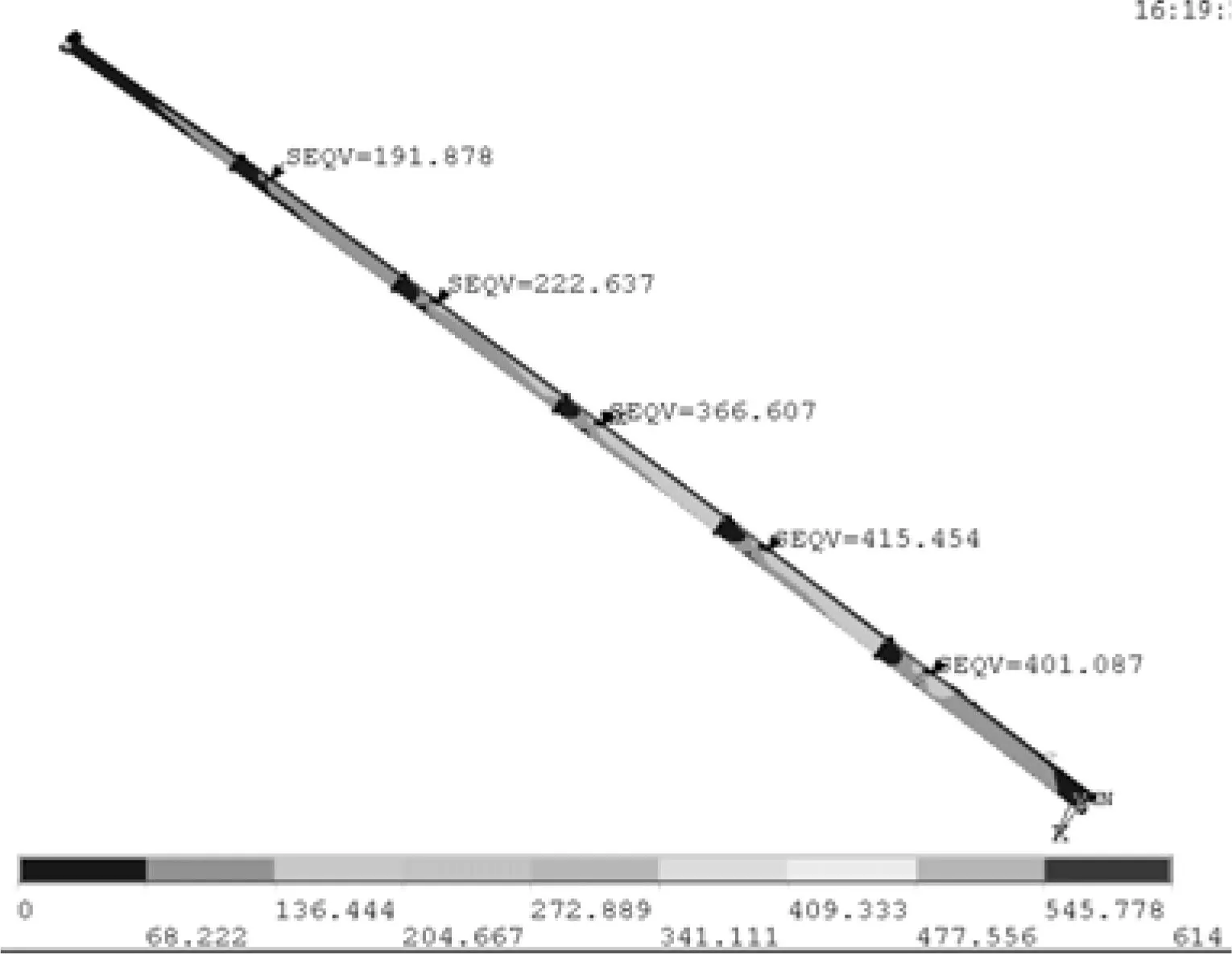
图4 整体应力分布

图5 一二节臂搭接处应力分布

图6 二、三节臂搭接处应力分布

图7 三、四节臂搭接处应力分布

图8 四、五节臂搭接处应力分布
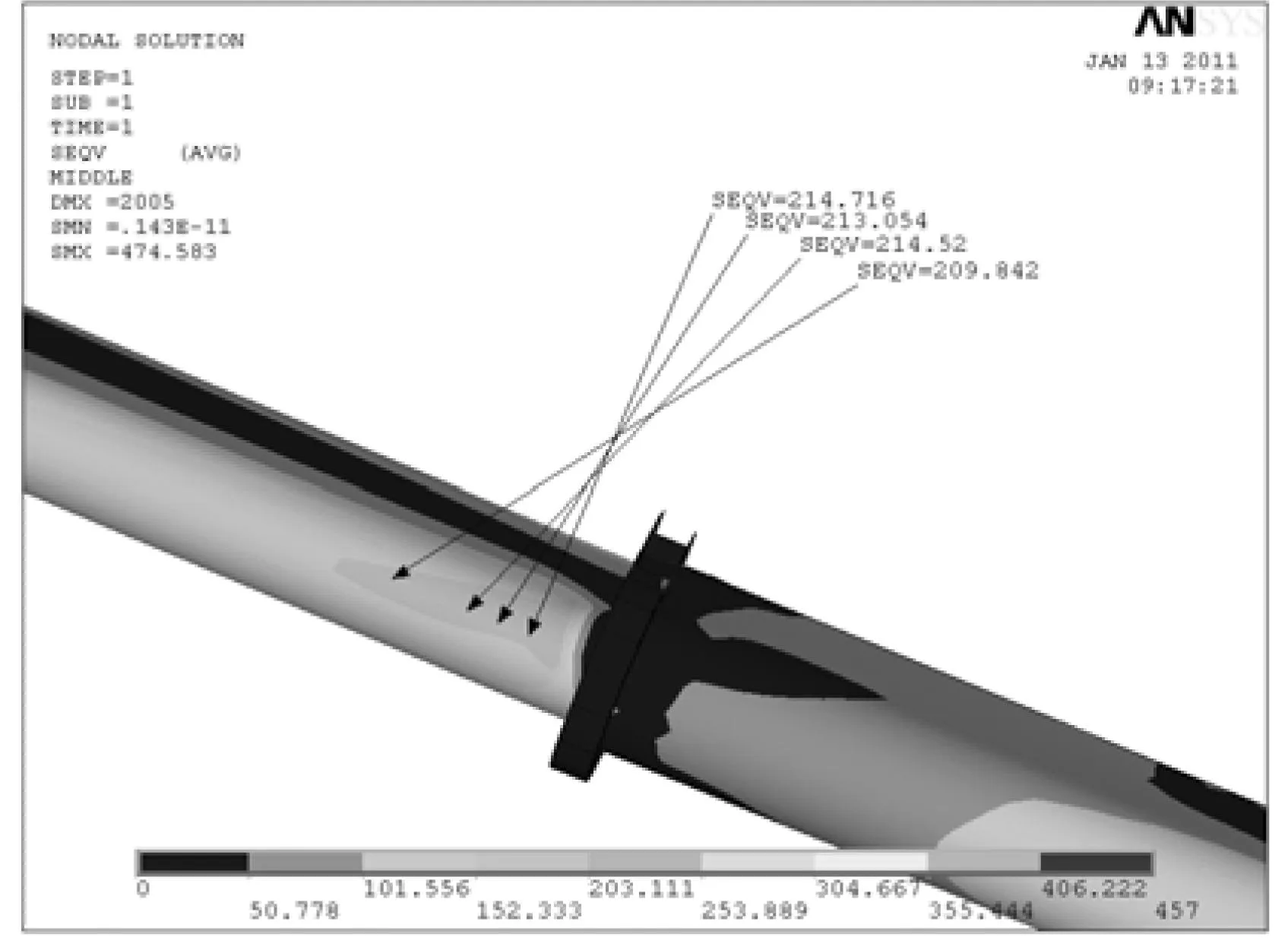
图9 五、六节臂搭接处应力分布
4有限元计算值与实测应力值的对比
4.1主臂的应力试验
试验利用YJ-18型静态电阻应变仪对主臂进行应力测试[9-10]。由于二、三、四、五、六节臂分别与前
滑块接触位置附近,及其变幅液压缸与基本臂铰接处均为潜在的危险应力区;两节臂搭接处,主臂截面尺寸发生变化,可能会产生应力集中;大部分起重机在实际的工作过程中,两节臂搭接的位置会出现变形,说明搭接处受力较大;主臂的截面形状是U型+圆弧+直线,布置时,U型布置在下侧,圆弧布置在上面,由于主臂弯曲变形,所以下侧受力较大,为防止圆弧过度处有压力集中,应变片布置在各节臂的危险截面上,具体位置如图10所示,各测点的实测值如表2所示。
表2各测力点的实测值

测点实测值/MPa测点实测值/MPa1-3787-3672-4008-4113-3989-4214-25610-3675-27811-3886-334--
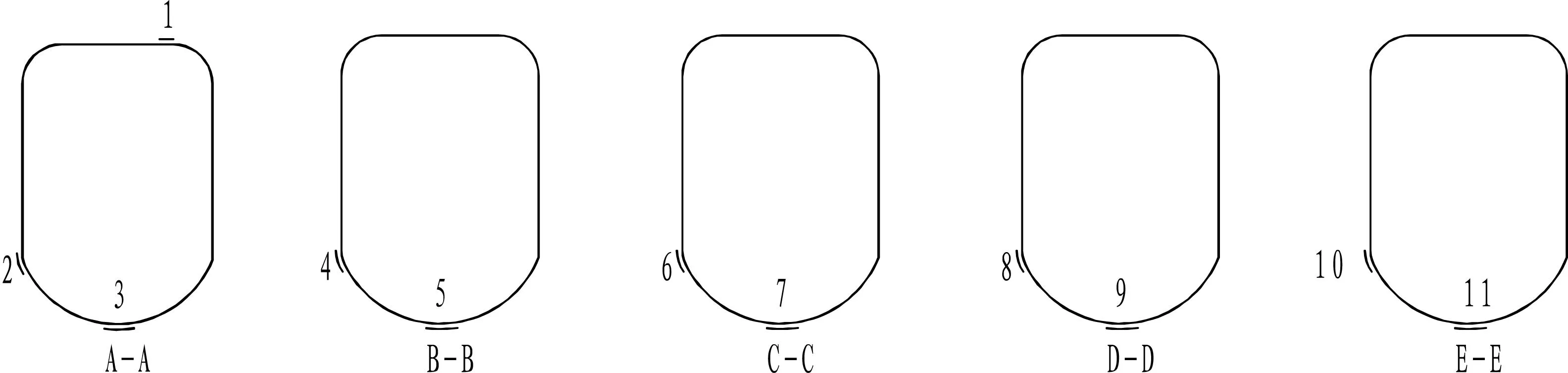
图10 主臂测力点分布图
4.2应力实测值与有限元计算值的对比分析
结构应力实验所测的是吊臂危险截面上的挤压应力值,用第四强度理论换算为等效应力,在最大起重力作用下将实验实测等效后的应力与ANSYS在实测点计算出来的等效应力相比较,如表3所示。
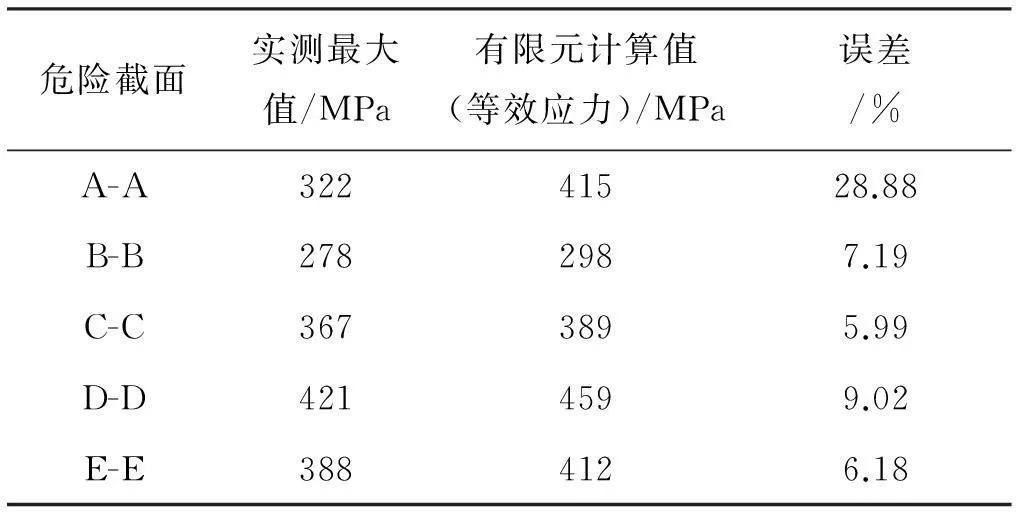
表3各危险截面上最大应力有限元值与实测值比较
危险截面实测最大值/MPa有限元计算值(等效应力)/MPa误差/%A-A32241528.88B-B2782987.19C-C3673895.99D-D4214599.02E-E3884126.18
由表3可知,所有测点的有限元应力计算值均小于材料的许用应力值614 MPa,其中,最大应力发生在第9测点,这与真实测试结果完全吻合,且在该测点处,有限元计算值与实测值的误差是9.02%,比较小。
在某些测点3中,误差值有些偏大,达到28.88%,这是因为吊臂实际结构复杂,简化后的有限元模型与实际模型之间存在着差别,尤其是在基本臂前端下滑块处模型模拟的差别,使得二级臂底板和折板与之相接触的局部区域应力偏大;另外,汽车起重机是一种短周期循环工作的机器,在工作过程中实际载荷具有多边性,而有限元模型无法完全模拟实际载荷的绝对真实性,所以有限元计算值和实际测量值之间存在误差是合理的。
综上分析,基于ANSYS有限元软件分析结果是可靠的。
5结束语
笔者对国内知名厂家的某型号汽车起重机主臂进行了理论强度计算,并利用有限元分析软件ANSYS计算该起重机吊臂在最大起重载荷作用下的应力和变形情况,计算得到,吊臂在该工况下满足强度要求。
最后对吊臂结构进行了实际应力测试,并将有限元计算值与实测值进行对比,结果显示:所有测点的有限元应力计算值均小于材料的许用应力值、误差小、且最大应力的发生位置有限元计算法与实测相一致;误差较大的测点3,是由于变幅液压缸与基本臂铰接处均为潜在的危险应力区,所以基于ANSYS有限元软件分析结果是可靠的。
参考文献:
[1]纪爱敏,彭铎,刘木南,等.QY25K型汽车起重机伸缩吊臂的有限元分析[J].工程机械, 2003,34(1):19-21.
[2]韦仕富,王三民,郑钰琪,等.某型汽车起重机吊臂的有限元分析及试验证[J].机械设计, 2011,28(6):92-96.
[3]张朝晖.ANSYS11.0结构分析工程应用实例解析[M].北京:机械工业出版社,2008:256.
[4]GB3811-83,起重机设计规范[S].
[5]徐李荣,袁泽喜.一起汽车起重机吊臂断裂事故的分析[J].中国特种设备安全,2007,23(7):58-59.
[6]姚海瑞.履带起重机主臂结构有限元计算[J].冶金设备,2015(1):30-32.
[7]孙书成,王彦涛,李建忠,等.汽车起重机折臂事故分析[J].工程机械,2010(8):68-71.
[8]刘文强,谭健敏.履带起重机主臂防后倾控制的分析[J].建筑机械,2015(1):86-89.
[9]宓为建,马捷,赵成.门坐式起重机主臂驾折断的原因分析[J].振动、测试与诊断,1999,3(1):54-57.
[10]黄志文,黎起富,李丽敏. 80t履带起重机主臂架有限元分析[J].建筑机械化,2009(11):48-52.
Strength analysis of the main arm of a truck crane based on ANSYS
ZHANGYan-yan1,ZHUMing-ming2,ZHOUYou-kung3
(1.Engineering Institute of Huanghe Science and Technology University, Zhengzhou 450063, China;2. Henan Entry-Exit Inspection and Quarantine Bureau, Zhengzhou 450003,China;3.Sany Limited by Share Ltd,Changsha 430100,China)
Abstract:By taking the telescopic boom structure of certain truck crane as the research object, its theoretical strength analysis was carried out. Based on the finite element analysis software ANSYS, the automobile crane telescopic boom of the finite element model was established, the telescopic boom stress distribution was analyzed under the functions of maximum torque, and the results of finite element analysis and the measured value were compared, and the results show that: the maximum stress position is consistent and the error is reasonable between the finite element calculation results and the measured results, and the results of the analysis based on ANSYS finite element analysis software is reliable.
Key words:truck crane;main arm;FEA ;strength calculation ;test
中图分类号:TH 2
文献标识码:A
DOI:10.3969/j.issn.2095-7386.2016.01.014
文章编号:2095-7386(2016)01-0061-05
基金项目:河南省教育厅教学质量工程项目(ZLG 201405).
作者简介:张燕燕(1981-),女,讲师,E-mail: 56106438@qq.com.
收稿日期:2015-07-11.修回日期:2015-11-17.
