馈能磁流变半主动悬架模糊滑模控制
2022-09-20葛宇超张弘扬
葛宇超, 刘 刚, 苗 丰, 张弘扬
(沈阳航空航天大学机电工程学院, 辽宁沈阳 110136)
引言
悬架系统是车辆的重要组成部分,用于衰减、降低路面激励带来的车身振动,对车辆的乘坐舒适性、行驶平顺性和路面附着性有较大的影响[1]。半主动悬架开始研究于20世纪80年代初[2],通过实时调节悬架系统的阻尼或刚度特性来改善车辆性能。相比于主动悬架,其结构更简单,能耗更少[3]。因此半主动悬架在车辆行业中的应用越来越广泛。
磁流变液是一类在磁效应下,可以迅速、可逆的从牛顿流体转化为非牛顿流体的智能材料[4]。磁流变减振器就应用了这一特点,磁流变减振器具有阻尼力可控性好、对高温适应性强、反应速度快等优点[5],能够很好地应用于半主动悬架。
传统的磁流变减振器工作时需要外部电源,对于悬架的振动能量也无法进行回收。因此,对悬架能量回收技术的研究成为近几年国内外学者的研究方向[6]。CHEN等[7]研究并验证了将直线电机应用于磁流变减振器的可行性。CHOI等[8]设计了利用直线电机受迫振动回收能量的馈能磁流变减振器,将电磁感应发电装置集成在磁流变减振器的活塞上,实现了振动能的收集。董小闵[9]提出一种利用滚珠丝杠回收能量的采集器,通过螺母的直线运动带动丝杠旋转,从而带动发电机旋转产生电能实现能量回收。
对于半主动悬架系统而言,采用合理的控制策略才能实现悬架良好减振性能。滑模变结构控制具有抗干扰能力强、鲁棒性好等优点,能够很好的运用于半主动悬架的控制中[10]。楼少敏等[11]基于滑模理论设计滑模控制器,并使用平滑函数缓解系统的抖振。秦武等[12]验证了基于天棚控制的滑模控制策略对半主动悬架控制的有效性。赵强等[13]验证了模糊滑模控制器的有效性。
基于此,针对单筒减振器需做体积补偿的特点,提出了一种馈能磁流变减振器结构,通过直线馈能和滚珠丝杠馈能相结合来实现能量的回收利用。并建立了相应的力学模型和馈能模型,以及相应的二自由度1/4车半主动悬架系统数学模型。提出了一种基于混合天地棚阻尼控制的滑模变结构控制策略,针对滑模控制系统的抖振问题,使用饱和函数替代符号函数,并运用模糊控制优化滑模控制器,从而改善系统的稳定性。最后,用谐波叠加法生成路面激励输入,分别对被动悬架,基于混合天地棚阻尼控制和基于模糊滑模控制的半主动悬架进行对比仿真分析,验证馈能磁流变减振器结构的可行性和模糊滑模控制策略的有效性。
1 馈能磁流变半主动悬架结构和原理
馈能磁流变半主动悬架系统如图1所示,该系统包含馈能磁流变减振器、弹簧、模糊滑模控制器和超级电容。车辆在行驶过程中,不平整的路面造成车身振动,控制器控制电容输出不同的电流,使得磁流变减振器产生相应的阻尼力实现减振,减振器的往复运动通过馈能装置实现能量回收。
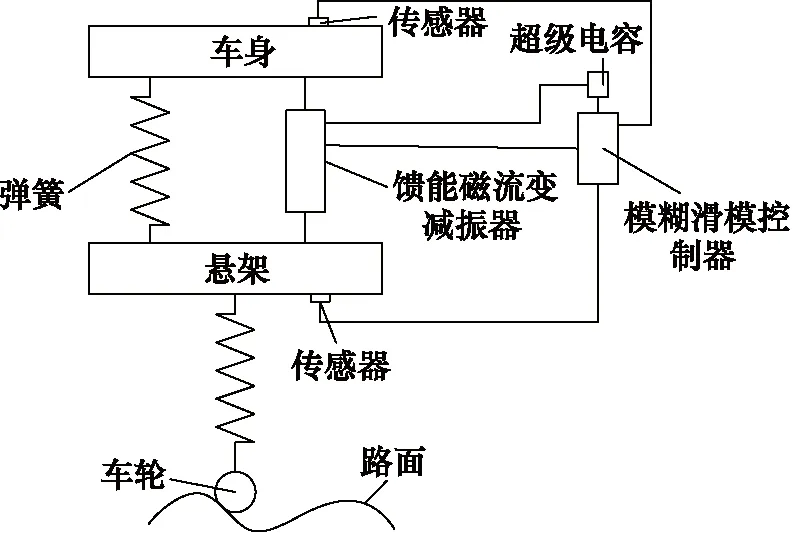
图1 馈能磁流变半主动悬架系统结构图Fig.1 Structure diagram of energy regenerative magnetorheological semi-active suspension system
其中,馈能磁流变减振器结构如图2所示,其主要由减振装置、馈能装置(包含直线馈能和滚珠丝杠馈能)、电能管理模块组成。由图2可知直线馈能装置的外筒随着活塞杆做往复直线运动,带动直线馈能装置外筒上的线圈相对减振器工作筒上的永磁铁做往复直线运动。同时活塞杆的往复直线运动迫使滚珠丝杠馈能装置的滚珠丝杠做往复直线运动,实现体积补偿。然后通过丝杠螺母传递,丝杠的直线运动使得螺母带动永磁环转子转动。发电线圈内部磁通量发生变化,产生感应电动势。并由电能管理模块将产生的交流电转换成直流电储存在超级电容中。

1.吊耳 2.下端盖 3.气囊 4.工作筒 5.丝杆活塞 6.活塞7.励磁线圈 8.导向器 9.隔磁材料 10.永磁铁 11.背铁12.直线馈能线圈 13.直线馈能装置外筒 14.上端盖 15.活塞杆16.外壳 17.电能管理模块 18.永磁环 19.导线20.滚珠丝杠馈能线圈 21.丝杠螺母 22.轴承23.滚珠丝杠 24.弹簧图2 馈能磁流变减振器系统结构示意图Fig.2 Schematic diagram of energy regenerative magnetorheological shock absorber system
2 馈能磁流变半主动悬架系统数学模型
2.1 馈能磁流变减振器力学模型
磁流变液力学特性采用Bingham本构模型如下:
(1)
式中,τ—— 剪切应力
τy—— 剪切屈服应力
η—— 动力黏度

sgn —— 符号函数,表示活塞运动时的速度方向
如图3为工作时的活塞杆受力情况。从图中可知活塞杆在运动时受到了环形阻尼通道的作用力F1,导向器小孔的作用力F2,弹簧对活塞杆的作用力F3,以及滚珠丝杠对螺母的轴向力F4。

图3 活塞杆受力示意图Fig.3 Schematic representation of piston rod force bearing
馈能磁流变减振器的阻尼力模型表示为:
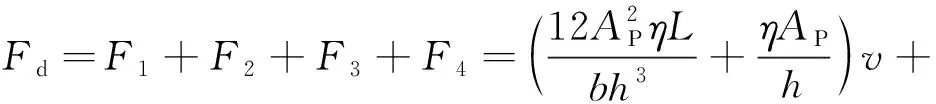
(2)
式中,x,v,a—— 分别为活塞运动的相对位移、相对速度以及相对加速度
L—— 阻尼通道的长度
b—— 通道宽度
h—— 磁流变减振器的阻尼通道间隙
AP—— 活塞有效面积
Cq—— 小孔流量系数,取0.82
Ak—— 导向器横截面的有效面积
A—— 单个小孔流通面积
ρ—— 液体密度
m—— 小孔的个数
kk—— 弹簧系数
Ds—— 丝杠活塞直径
D1—— 活塞杆直径
D4—— 工作筒内径
κ—— 发电装置发电系数
M—— 发电装置转子转动惯量
l—— 丝杠导程
n—— 传递效率
在频率为2 Hz,振幅为25 mm的正弦激励下,输入0, 0.2, 0.4, 0.6, 0.8, 1 A的励磁电流,馈能磁流变减振器的力学特性如图4所示。
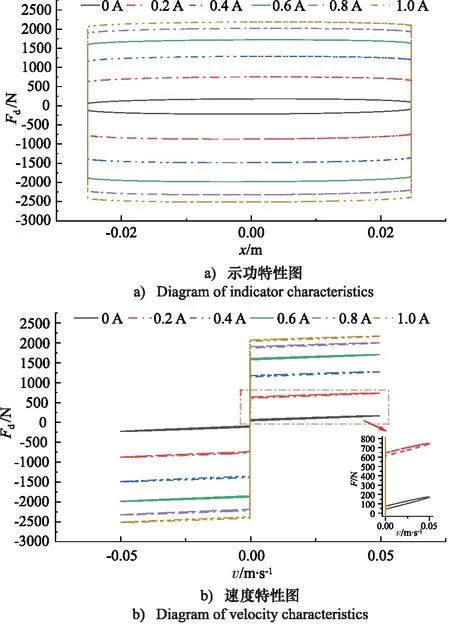
图4 馈能磁流变减振器阻尼力特征Fig.4 Damping force characteristics of energy regenerative magnetorheological shock absorber
从图4可见,馈能磁流变减振器的阻尼力在220~2500 N范围内变化,能够满足馈能磁流变减振器的减振要求。
2.2 馈能磁流变减振器馈能模型
馈能磁流变减振器的馈能模型分为直线馈能和滚珠丝杠馈能两部分。
直线馈能部分馈能功率可表示为[14]:
(3)
式中,N—— 发电线圈的匝数
E—— 直线馈能部分的感应电动势
φg—— 轴向方向气隙内的磁通量
ι—— 直线馈能部分的磁极距
x1—— 动子运动位移
v1—— 动子的运动速度
R—— 直线馈能发电线圈的电阻
R1—— 活塞励磁线圈的电阻
滚珠丝杠馈能部分采用三相交流电磁能量转换器。滚珠丝杠馈能部分输馈能功率可表示为[15]:

(4)
式中,Uph—— 单相开路电压
Uz—— 开路直流电压
R2—— 滚珠丝杠馈能发电线圈的电阻
N1—— 绕于齿上单相的线圈数
B—— 间隙的平均磁通密度
Lm—— 动子轴轴向有效长度

vs—— 丝杠的轴向速度
D—— 转子内径
σ—— 磁漏系数
减振器回收总能量为:
(5)
路面输入能量为:
(6)
式中,xt—— 非簧载质量位移
xr—— 路面激励
kt—— 轮胎刚度
Ft—— 轮胎动载荷
T—— 工作时间
磁流变减振器馈能效率为:
(7)
2.3 二自由度半主动悬架系统数学模型
二自由度半主动悬架系统数学模型如图5所示。
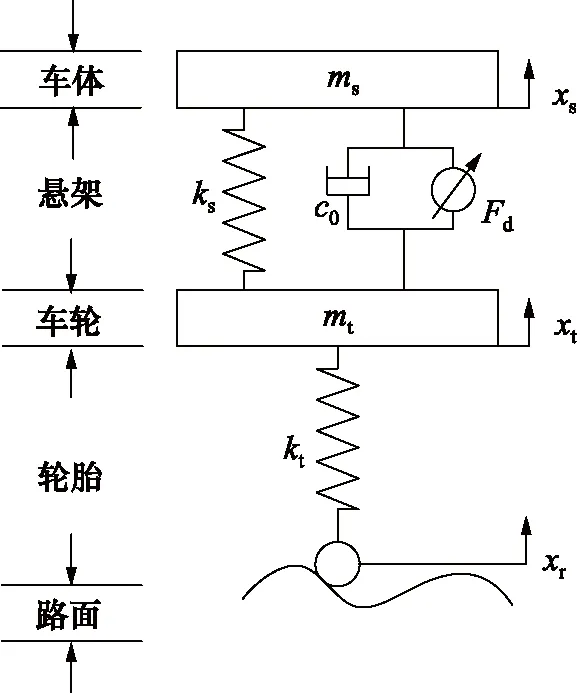
图5 二自由度半主动悬架系统数学模型Fig. 5 Mathematical model of two degrees of freedom semi-active suspension system
根据牛顿运动定律,可得:
(8)
(9)
式中,ms—— 簧载质量
mt—— 车轮质量
xs—— 簧载质量位移
xt—— 非簧载质量位移
xr—— 路面激励
ks—— 弹簧刚度
kt—— 轮胎刚度
c0—— 零场阻尼
Fd—— 半主动控制力
令:
(10)
将式(2)和式(10)代入式(8)、式(9)可以转化为:

(11)

(12)
3 模糊滑模控制器
3.1 滑模控制器的参考模型
为了同时提高车辆的平顺性和操稳性,以混合天地棚阻尼控制模型作为参考模型[3],如图6所示。
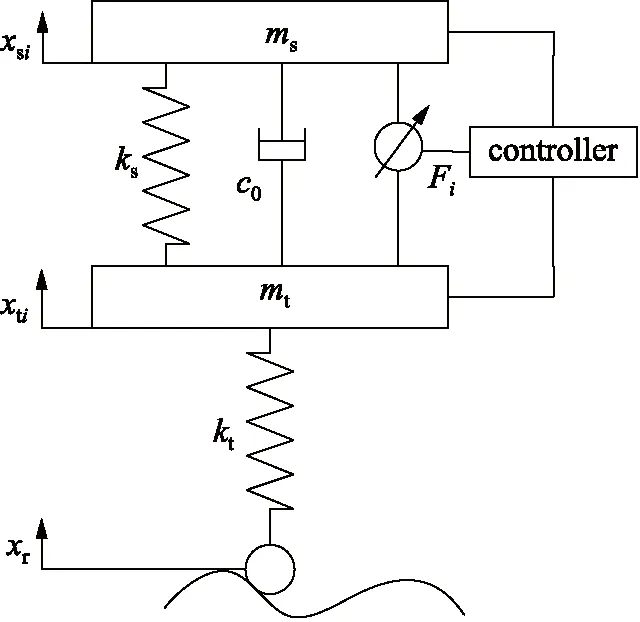
图6 混合天地棚阻尼控制模型Fig.6 Damper control model of hybrid reference
根据牛顿运动定律,可得:

(13)

(14)
式中,xsi—— 簧载质量位移
xti—— 非簧载质量位移
Fi—— 半主动控制力
其中混合控制力表示为:
Fi=αFsk+(1-α)Fgr
(15)
式中,Fsk/Fgr—— 天棚/地棚阻尼控制力
α—— 加权系数,取值0.8
3.2 滑模控制器的设计
滑模控制器可以迫使实际系统在一定特性下沿着参考系统的状态轨迹做小幅高频的上下运动,即所谓的滑动模态。定义误差矢量e为实际系统与参考系统的速度差、位移差以及位移差积分。
取变量:
(16)
误差动力学方程为:

(17)
式中,A,B,E,G,H,I—— 系数矩阵
u—— 控制输入
w—— 参考模型混合控制力输入
v—— 干扰输入(路面激励输入)
设计切换面函数为:
s=ce=c1e1+c2e2+c3e3
(18)
通常c3取1,可得滑动模态的运动微分方程:
(19)

根据式(17)和式(18)可得:

(20)
则输出阻尼力u为:
(21)
ueq=-(cG)-1(cAe+cBX+cEX′+cHw+cIv)
(22)
由于实际模型受到外界干扰,为改善系统稳定性,采用等速趋近律来改善趋近效果:

(23)
式中,ε增益系数,表示系统运动点趋近切换面的速率。ε小,趋近速度慢;ε大,趋近速度较大,系统的抖动也较大。最终系统滑模控制的控制力u为:
u=ueq-(cG)-1εsgn(s)=ueq+usmc
(24)
式中,usmc—— 滑模控制补偿力
系统的可变阻尼力为:
(25)
3.3 饱和函数
滑模控制鲁棒性好、抗干扰能力强,可以很好地适应半主动悬架系统。但滑模控制在本质上的不连续开关特性会引起系统的抖振,为缓解这一问题,采用饱和函数替代符号函数[16],即:

(26)
式中,s—— 切换函数
Δ —— 边界层,k=1/Δ
根据切换函数s的范围,令Δ=0.02,进行仿真,由图7可知,由于符号函数的不连续开关特性,使得滑模控制补偿力usmc发生抖振现象,而使用饱和函数可以缓解这一现象,提高系统稳定性。

图7 不同函数对滑模控制补偿力的影响Fig.7 Influence of different functions on compensating force of sliding mode control
3.4 模糊滑模控制器
为进一步消除抖振,采用模糊控制优化滑模控制器。模糊控制基于人工经验,不需要系统的准确模型,通过模糊控制规则的制定来实现非精确控制[10]。模糊控制通过调整滑模控制的边界层来补偿系统的不确定性,模糊控制与滑模控制相结合可有效缓解抖振的影响,改善系统稳定性,模糊滑模控制器如图8所示。
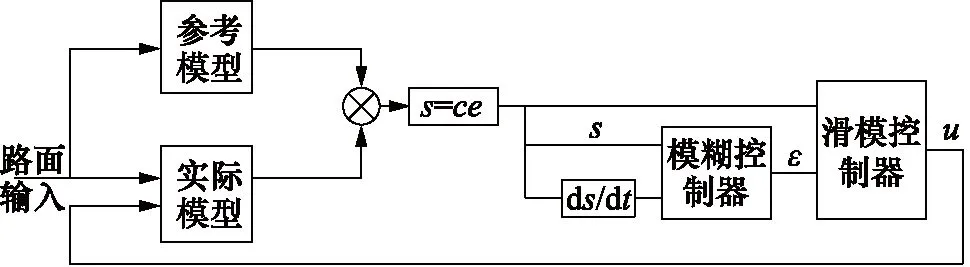
图8 半主动悬架模糊滑模控制器的结构框图Fig.8 Structural diagram of fuzzy sliding mode controller for semi-active suspension


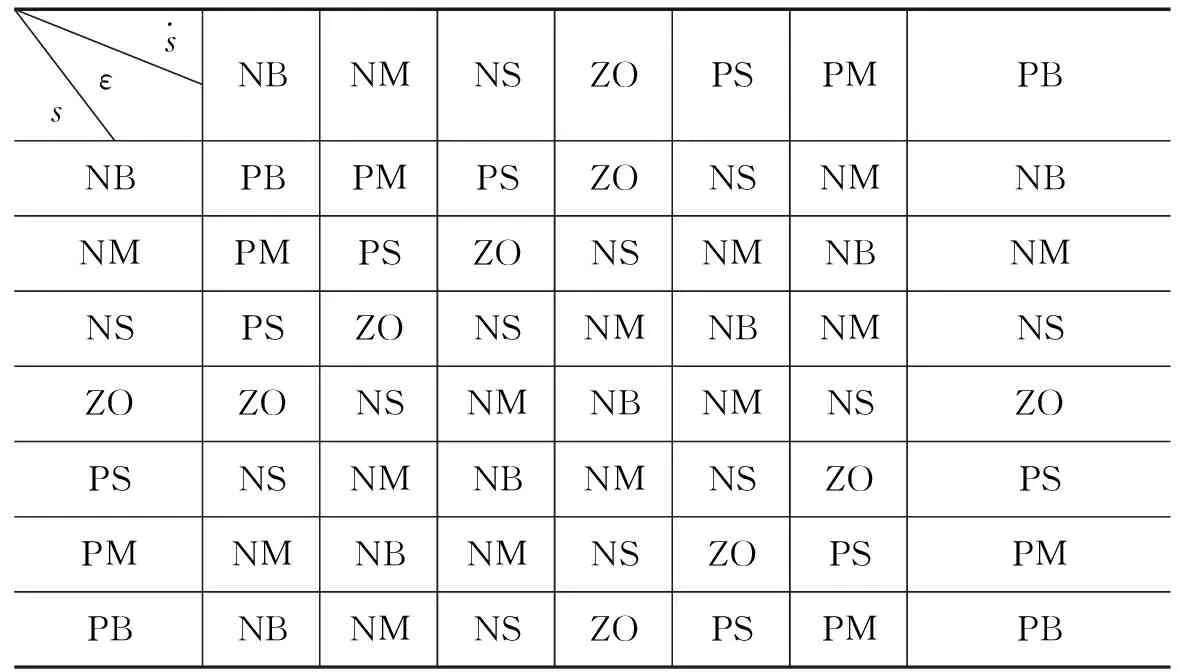
表1 模糊控制规则Tab.1 Fuzzy control rule
4 半主动悬架模糊滑模控制仿真
为验证模糊滑模控制策略的有效性,在 Simulink中搭建模型,选用随机路面作为输入,随机路面激励采用谐波叠加法,基于谐波叠加法生成的路面激励可表示为[1]:
(27)
式中,θk—— 在区间[0,2π]上生成的随机数
Gxr(f) —— 时间频率功率密度
m—— 将频率区间[fmin,fmax]划分成小区间的个数
fmid_k—— 每个小区间的中间值
Δfk—— 小区间的长度
取C级路面不平度系数Gxr=256×10-6m3,车速v=10 m/s,得到如图9所示的谐波叠加法产生的随机路面波形。表2为半主动悬架系统主要参数。

表2 半主动悬架系统主要参数Tab.2 Main parameters of semi-active suspension system
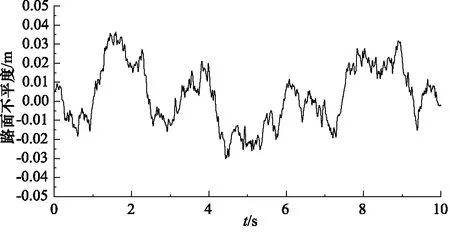
图9 谐波叠加法产生的随机路面波形Fig.9 Random road waveform generated by harmonic superposition method
为了分析模糊滑模控制半主动悬架的减振性能,对随机路面激励下的被动悬架,混合天地棚控制半主动悬架和模糊滑模控制半主动悬架进行对比仿真分析。图10~图12分别为该半主动悬架在不同控制策略下各性能曲线。从图中可知,基于模糊滑模控制的半主动悬架相比被动悬架和基于混合天地棚控制的半主动悬架的减振性能有明显改善。
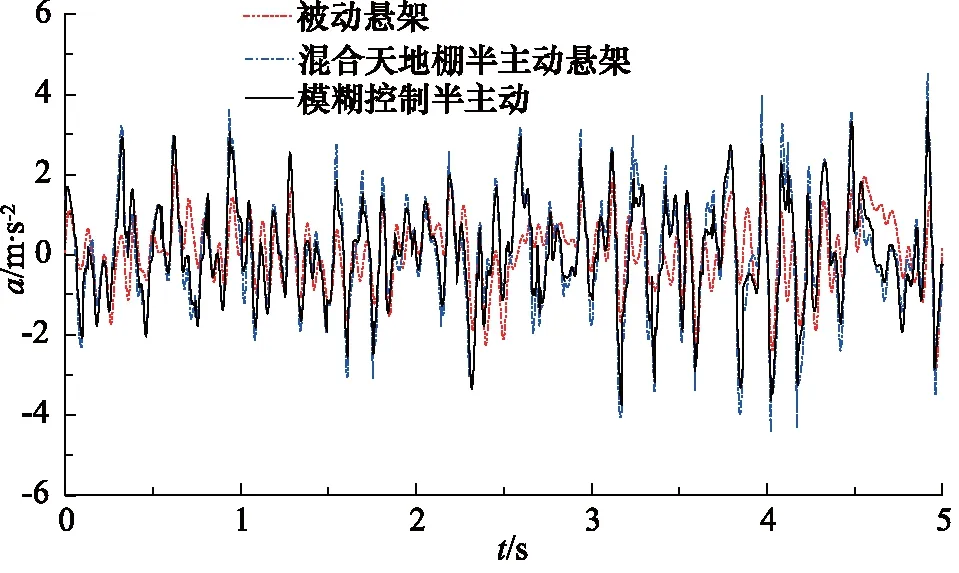
图10 车身加速度Fig.10 Body acceleration

图11 悬架动挠度Fig.11 Suspension dynamic deflection
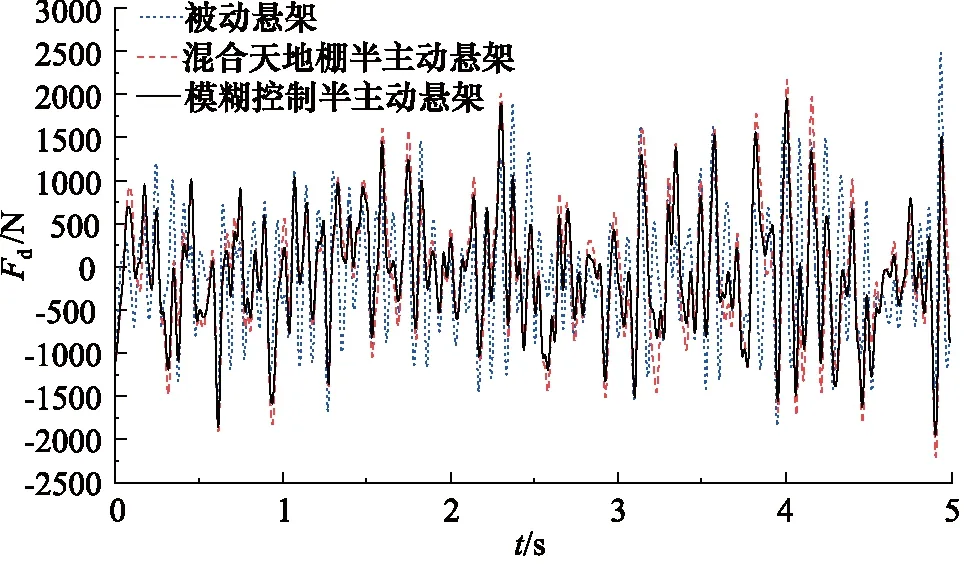
图12 轮胎动载荷Fig.12 Tire dynamic load
表3为悬架在不同控制下的各项动力学性能指标的均方根值。由表3可知,在随机路面激励下,基于模糊滑模控制的半主动悬架的车身加速度、悬架动挠度和轮胎动载荷的均方根值相比于被动悬架和基于混合天地棚控制的半主动悬架分别降低了21.85%,56.19%,55.42%和40.20%,33.3%,48.67%,表明了该半主动悬架在模糊滑模控制下具有更好的减振性能。
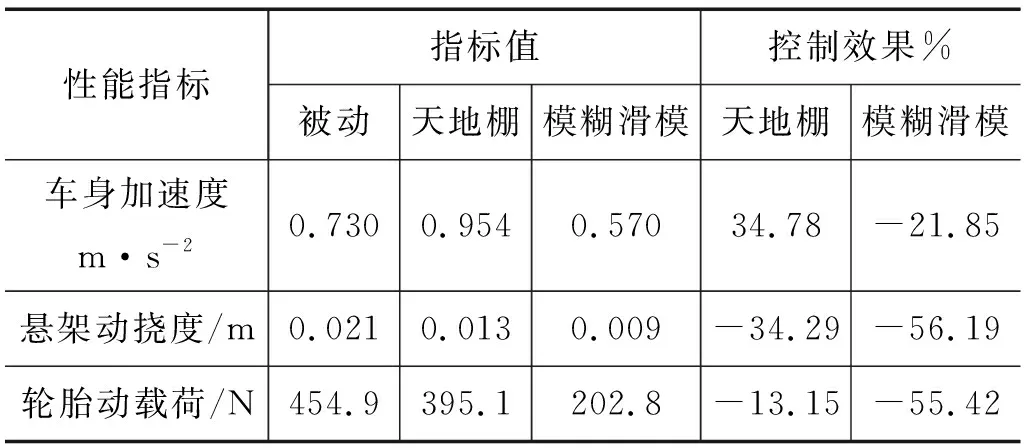
表3 随机路面下不同控制半主动悬架性能指标及控制效果Tab.3 Performance index and control effect of different control semi-active suspension on random road surface
为了分析模糊滑模控制半主动悬架的馈能性能,在随机路面激励下,对混合天地棚控制半主动悬架和模糊滑模控制半主动悬架进行对比仿真分析。图13~图17为该半主动悬架在不同控制策略下的各项馈能相关曲线。其中悬架总能量为悬架馈能能量与耗能能量之差。
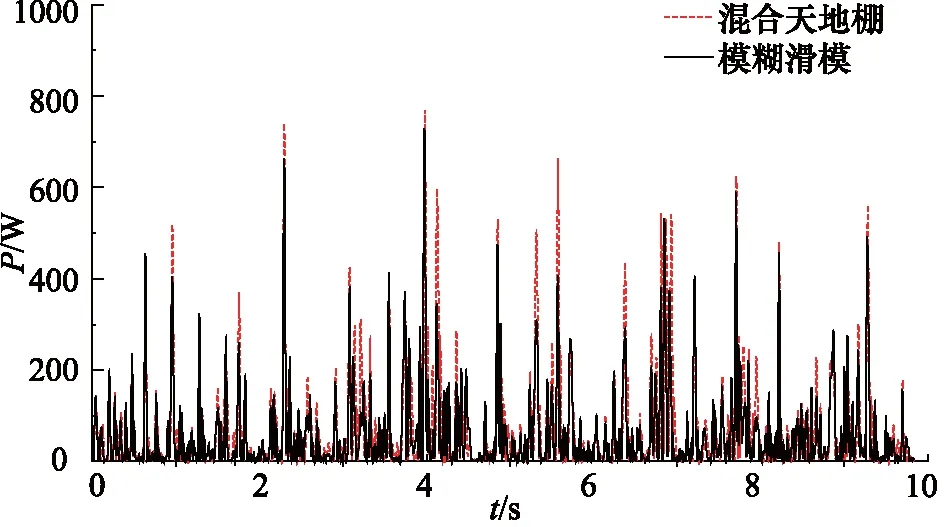
图13 不同控制下的路面输入功率Fig.13 Road input power under different control

图14 不同控制下的馈能功率Fig.14 Energy regenerative power under different controls

图15 不同控制下的馈能效率Fig.15 Energy regenerative efficiency under different control

图16 不同控制下的耗能功率Fig.16 Power dissipation under different controls

图17 不同控制下的悬架系统总能量Fig.17 Total energy of suspension system under different control
由图和表4可知,基于模糊滑模控制的半主动悬架相对于基于混合天地棚控制的半主动悬架耗能更小,馈能效率更高。该半主动悬架系统总能量大于零,说明该悬架在满足自身能耗的同时能够实现对外输出电能,满足了悬架馈能的设计初心,验证了该悬架的可行性,为进一步研究奠定了基础。
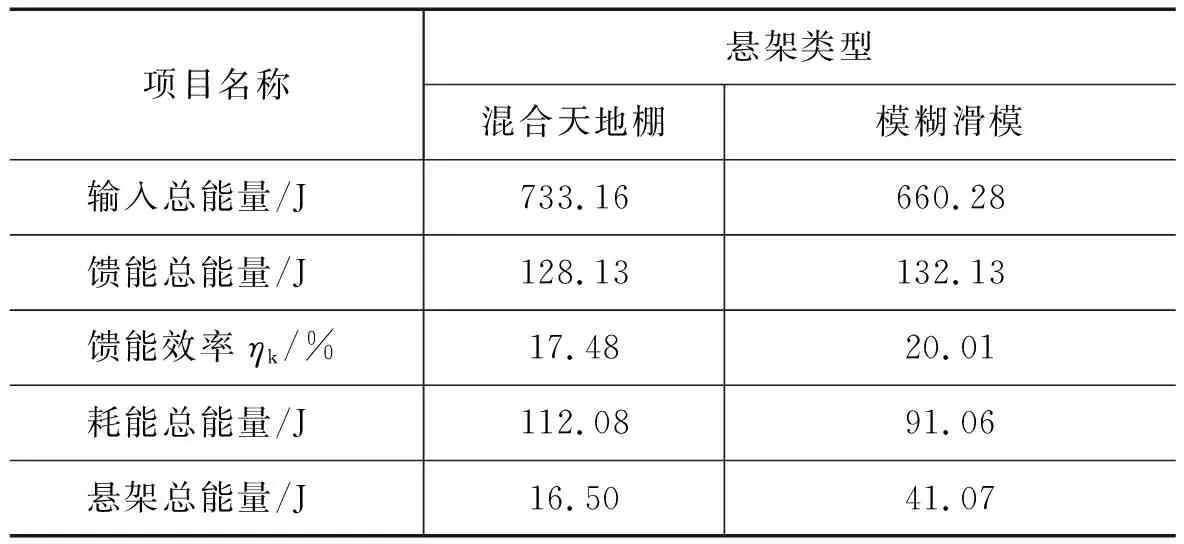
表4 不同控制下悬架的馈能特征Tab.4 Energy regenerative characteristics of suspension under different control
5 结论
(1) 针对单筒减振器需做体积补偿的特点,提出了一种基于直线馈能和滚珠丝杠馈能相结合的新型单筒馈能磁流变减振器的结构,说明其工作原理,建立了相应的力学模型和馈能模型,及二自由度半主动悬架系统数学模型;
(2) 以混合天地棚阻尼控制系统为参考模型,设计滑模控制器,为缓解系统抖振,使用饱和函数代替符号函数,并运用模糊控制优化滑模控制器,改善系统稳定性;
(3) 用谐波叠加法生成路面激励输入,分别对被动悬架,基于混合天地棚阻尼控制和基于模糊滑模控制的半主动悬架进行对比仿真。结果表明,基于模糊滑模控制的半主动悬架减振性能更好,能耗更小,且有良好的馈能性能,验证了馈能磁流变减振器结构的可行性和模糊滑模控制策略的有效性。
