新型钢板桩液力自旋式喷嘴设计及流场分析

邓智超， 赵鲲鹏， 王贵和， 贾苍琴， 冯梓波

(中国地质大学工程技术学院， 北京 100083)

引言

钢板桩是适用于基坑深度超过5 m的一种深基坑连续性支护桩，具有环保、水密性好、施工工期短、可重复利用，适用于作业面狭窄的工程环境等特点，现广泛用于救灾抢险、堤岸、桥基、地下管廊等工程中。钢板桩的施工可简单概括为：振动沉桩或静压沉桩后，配合钢支撑或围堰形成支护结构，待内作业完成后拔出钢板桩，进行注浆回填。随着我国地下空间朝着深而广的方向开发[1-3]，基坑支护过程中遇密实土层的频率逐年上升，传统的沉桩方式在应对密实土层时，常常会出现桩端和桩侧阻力过大而难以沉桩的问题。因此，如何快速高效地将钢板桩沉至标高具有很高的实际应用价值。

针对这一问题，国内外学者对水射流破土机理进行了分析，并对其应用于基坑支护工程的可行性进行了许多研究[4-9]。李仁民等[10]首次在国内钢板桩应用实例中提出“辅助射水法”帮助钢板桩在高粘聚力密实红砂岩中沉至设计标高，并与传统沉桩方式进行了效果比对；李仁民等[11]和薛峰[12]在大直径圆形钢板桩围堰支护工程中提出了适用于钢板桩沉桩的“水刀”引孔系统，并提供了初步的制作方法；何炳泉等[13]在超长钢板桩支护工程中提出了静压植桩技术代替传统振动沉桩技术，结合“水刀”引孔系统针对砂质地层进行施工；周严为等[14]和胡志勇[15]对 “水刀”引孔系统的制作和安装进行了系统性的归纳和总结。由于未能将水射流破土机理与钢板桩实际应用需求相结合，水射流辅助沉桩技术在上述的钢板桩实际应用中尚未发挥其最佳性能。金宝林等[16]研究了不同泵压下的水射流对钢板桩在高粘聚力、硬塑性粉质黏土层中沉桩速率的影响；仲如冰[17]通过仿真软件模拟6种不同形状的喷嘴，研究被射流破坏后土体的最大、最小应力，并用室内模型试验对比了不同射流流量下钢桩模型的锤击数；JAROA等[18]提出了优化后的水射流系统，并通过对比现场试验监测数据得出，振动沉桩过程中产生的土塞效应和桩身内锁效应在水射流的辅助下有了显著的减小。上述研究将水射流破土原理与水射流辅助沉桩系统研发相结合，对水射流辅助沉桩技术的研究有了更进一步的发展。

目前，现有应用于水射流辅助钢板桩沉桩工艺中的喷嘴多为常见的喷嘴结构，圆柱形、锥形喷嘴结构虽能提供较强的冲击力，但是射流影响面积小，软化土体和润滑桩身的效果不佳；扇形喷嘴能够提供较大的射流影响面积，但射流强度衰减较快，对土体的冲击力不足。本研究旨在设计一种专用于水射流辅助钢板桩沉桩的液力自旋式喷嘴，通过液力驱动喷嘴旋转产生旋转喷射流，在保证冲击力的前提下，扩大射流影响范围，起到既能够充分破坏土体结构，又能润滑钢板桩桩身，减小桩侧阻力的作用，通过研究旋喷口的不同结构参数下水刀喷嘴的出口流速以及水射流驱动喷嘴旋转的转矩大小变化规律，为该构件的结构优化提供参考依据。

1 液力自旋式喷嘴工作原理

液力自旋式喷嘴主要由护筒、旋喷头、密封圈、旋转盖、无缝钢管、推力球轴承等构成，其结构如图1a所示。护筒、无缝钢管Ⅱ依次相接于无缝钢管Ⅰ下方，推力球轴承Ⅰ的座圈装配在旋喷头卡口处，轴圈装配于无缝钢管Ⅱ卡口下侧，推力球轴承Ⅱ的轴圈安装于特制无缝钢管Ⅱ卡口上侧，座圈装配在旋喷头封口处下方，通过2个推力球轴承的钢球保持架实现部件之间的相对转动，旋转盖通过螺栓与旋喷头接合，保证构件能在承受轴向力的情况下转动。

工作过程：水流经过高压水泵增压，通过高压软管和无缝钢管输送至喷嘴，通过3个射流口产生高压射流，由图1b 可以看出，流体域由中心腔室和3个射流口组成，旋喷头的2个斜射流口在OXZ截面上的投影关于原点对称，二者的投影互相平行，流体进入斜射流口时，受到壁面的约束，距OYZ截面较远侧壁面压迫流体转向，产生离心力冲击壁面，与斜射流口的射流反推力共同提供旋转动力，使得推力球轴承带动旋转体(旋喷头、旋转盖)转动，产生旋转喷射流。

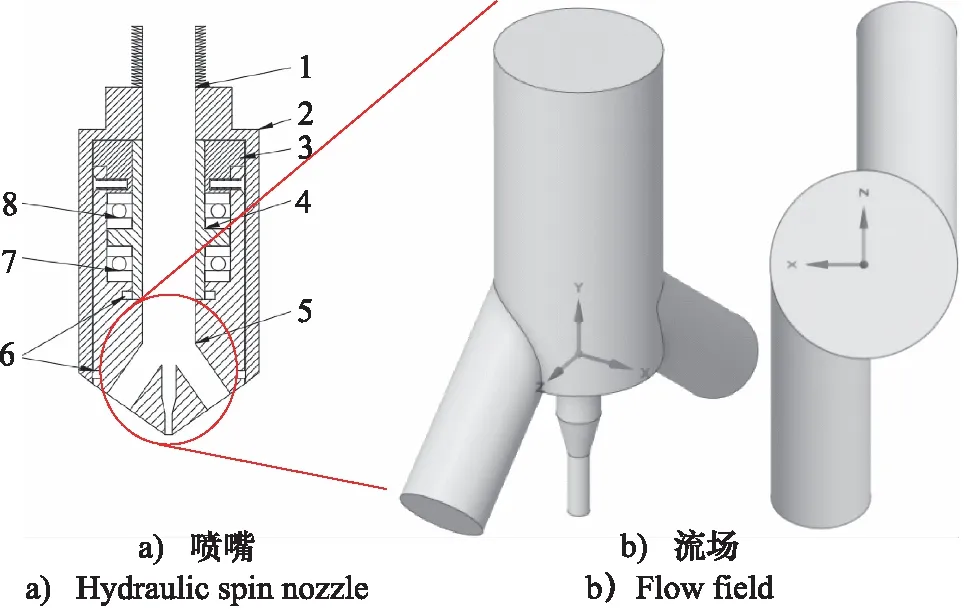
1.无缝钢管Ⅰ 2.护筒 3.旋转盖 4.无缝钢管Ⅱ5.旋喷头 6.密封圈 7.推力球轴承Ⅰ 8.推力球轴承Ⅱ图1 新型液力自旋式喷嘴及流场结构简图Fig.1 Structure diagram of new type hydraulic spin nozzle and flow field

2 液力自旋式喷嘴数学模型

旋转体的旋转动力由两部分提供：一部分由斜射流口的射流反推力提供；另一部分由斜射流口壁面压差提供。

由动量定理可知，理想净推力等于单位时间内动量的增量，即：

(1)

在射流稳定后，旋转体克服密封圈和土的摩阻力开始定轴转动，斜射流口推力计算公式为：

(2)

其中沿Z轴方向的分量为斜射流口反推力为旋转体提供的旋转动力。

由动量定理可知，质点系动量的增量等于作用于该质点系上的外力的冲量，即：

(3)

液体对斜射流口壁面作用力计算公式为：

(4)

其中沿X轴方向的分量为水对斜射流口壁面作用力为旋转体提供的旋转动力。

式中， Δφ—— 单位时间经过喷嘴的动量增量

A—— 斜射流口的出口面积

ρ—— 流体密度

Q—— 斜射流口射流流量

ν—— 流体对旋转体力的作用点的线速度

β1，β2—— 冲量修正系数

该机构内总水头损失分为沿程水头损失和局部水头损失，因为机构尺寸短小，沿程损失可忽略，局部损失主要集中在3个位置，即旋喷头的中心射流口处和2个斜射流口进口处，能量损失叠加原理总水头损失公式为：

(5)

式中，hf—— 沿程水头损失

hj—— 局部水头损失

li—— 中心腔室的入口至斜射流口的出口长度

di—— 斜射流口管径

vi—— 局部装置处流速

λi—— 沿程阻力系数

ζi—— 局部阻力系数

n，m—— 流场内沿程损失和局部损失处数量

可将斜射流口进口处看成2个锐缘斜进口的叠加，由于沿程损失可忽略，因此总损失为：

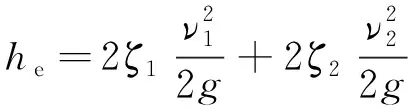
=2[0.505+0.303sin(-α)+0.226sin2(-α)]×

(6)

式中，ζ1—— 第一个锐缘斜进口局部损失系数

ζ2—— 第二个锐缘斜进口局部损失系数

α—— 斜射流口水平面夹角

e—— 斜射流口偏心距

r—— 中心腔室半径

本研究范围内，偏心距取值为0～3.5 mm，在取值范围内局部阻力系数与偏心距呈正相关。

3 液力自旋式喷嘴流体仿真模型

3.1 几何模型

根据水射流辅助钢板桩沉桩技术的实际施工工况，通过改变斜射流口与水平面的夹角大小和斜射流口的偏心距2个结构参数，来研究喷嘴的出口流速以及旋转体的转矩变化情况。流体域结构：中心腔室直径15 mm，长度25 mm；斜射流口直径8 mm，轴线长度25 mm；中心射流口入口直径4 mm，长度4 mm；出口直径2 mm，长度6 mm，收缩角13°。

3.2 网格模型

网格划分的数量和质量会直接影响计算精度和准确性。网格数目越高，计算精度越高，计算机运算所需要的时间也越长；网格质量越高，计算结果与实际越相符。在确定网格模型时，对其进行网格质量评价和网格数量无关性评价。

1) 网格数量无关性验证

通过表1可见，当网格规模为6万以上时，弯曲管道的局部损失系数相对误差小于2%。

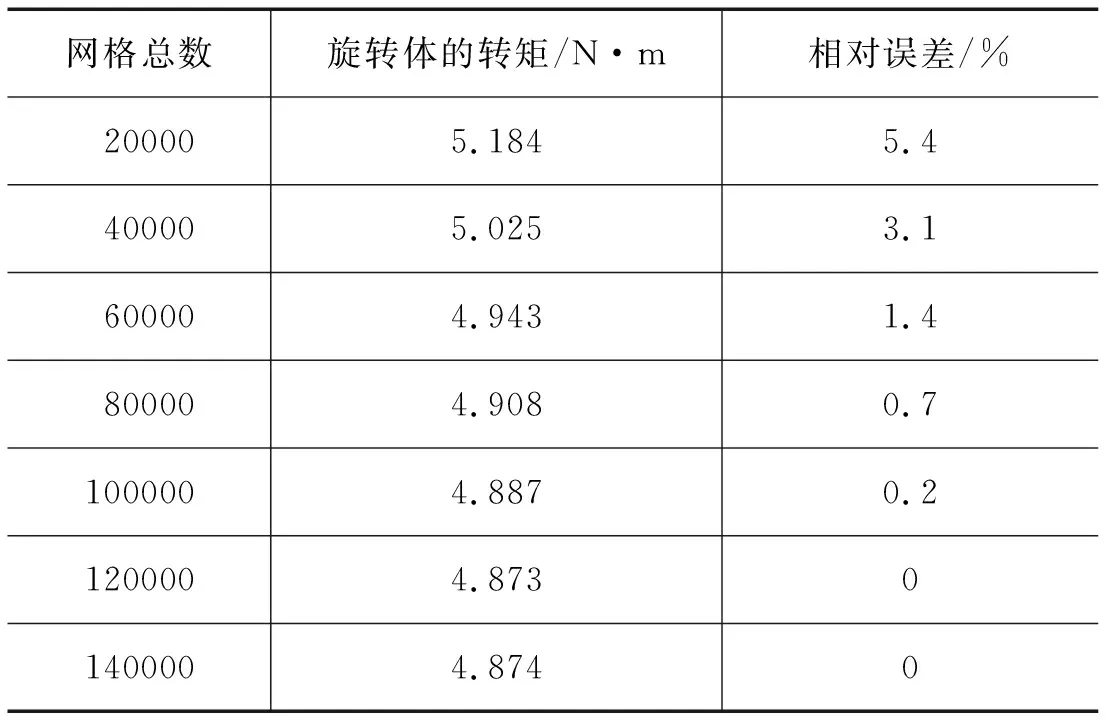
表1 网格数与旋转体的转矩关系Tab.1 Relationship between grids number and rotating body torque

2) 网格质量评价

检查网格质量，对质量较差的网格进行优化，从而保证计算结果的准确性。由于液力自旋式喷嘴的中心射流口与整体尺寸相差较大，为保证其计算精度，选择在中心射流口处进行网格加密，如图2所示。在综合考虑计算结果和计算精度的情况下，选取网格数为106738进行计算，其正交质量平均值为0.772，倾斜度平均值为0.227，均满足标准要求。

图2 流场网格模型Fig.2 Grid model of flow field

3.3 计算条件

相较于标准k-ε模型，RNGk-ε模型在拥有较高的稳定性和精度的前提下，不仅考虑了旋转效应，使其计算强旋转流动时精度得到了提升，还更加适合速度梯度较大的流场计算。结合液力自旋式喷嘴旋喷头处的流场结构特点，本研究选择采用RNGk-ε湍流模型。

射流介质为液态水，保持其默认参数。进口设置于中心腔室顶面，采用压力入口边界，出口分别设置于斜射流口和中心射流口的出口处，采用压力出口边界，管壁为壁面边界，默认静止无滑移边界。结合实际工况，设置入口压力为10 MPa。

根据液力自旋式喷嘴结构流体驱动喷嘴产生自旋运动的特点，采用弹簧光滑法、局部网格重构法以及SIX DOF动网格方法对其进行研究。使用Profile文件定义旋转体的质量、转动惯量，限制其沿X，Y，Z轴平动以及绕X，Z轴的转动。选取计算时间步长Δt=1.0×10-4s。

4 仿真结果分析

4.1 变斜射流口偏心距分析

1) 转矩随斜射流口偏心距变化规律

为直观地体现喷嘴转矩随偏心距的变化规律，展示斜射流口偏心距e分别为0.5，1.5，2.5，3.5 mm时的压力分布情况，如图3所示。

图3 变斜射流口偏心距压力云图

根据旋喷头的流场结构来看，流体经中心腔室分流后，分别沿2个斜射流口和中心射流口流出，产生射流。中心腔室下边界处的流场由于斜射流口的偏心、倾斜、直径突然减小而发生急变。与弯管水流对壁面作用原理相似，流体进入斜射流口后，受到壁面的约束，距OYZ截面较远侧的壁面压迫流体转向产生离心力，冲击壁面，导致远侧壁面的压力增大，而距OYZ截面近侧壁面发生边界层分离，压力减小，由此产生转矩使得旋转体绕轴转动。由图3可以看出，偏心距较小时，斜射流口壁面的压力分布没有明显的变化，说明由于偏心距较小，流体在此发生转向的转角较小，沿远侧壁面法线方向的速度分量较小。再由恒定总流动量方程可知，在修正系数、流量和密度不变的情况下，流速与外力成正比，故得出作用于远侧壁面法线方向的力较小，使得压力分布没有明显的变化。当偏心距大于2.5 mm时，由于偏心距的增大，流体在此发生转向的转角变大，作用于远侧壁面法线方向的力也变大，压力显著增大，近侧壁面越发靠近OYZ截面，边界层分离点逐渐前移，压力增长较为平缓，使得压力分布发生明显的变化。说明随着偏心距的增大，斜射流口壁面压差逐渐增大，且偏心距越大，压差增大得越快。

在不改变斜射流口与水平面夹角的情况下，以0.25 mm作为间距，在0～3.5 mm之间选取15个特征值作为斜射流口偏心距，分别建立15个不同流体域模型所产生旋转体的转矩M曲线，如图4所示。在研究范围内，旋转体的转矩大小是随着偏心距的增大而稳步增大。经仿真监测结果得，在这15个流体域模型中，射流反推力对旋转体所产生的转矩不足流体对斜射流口壁面作用后所产生转矩的0.6%，旋转体转矩主要由斜射流口壁面压差所提供。结合上述射流口偏心距的变化导致壁面压差发生变化规律来看，虽然壁面压差随着偏心距的变大而增大得越快，但是偏心距的变化也导致了转矩的力臂发生变化。由图3可以看出，随着偏心距的增大，远侧的壁面由于圆柱的几何结构特点而向OXY截面靠近，导致其力臂减小，且偏心距越大，其变化得越快。由此可分析得出，随着偏心距的增大，壁面压差增大，且偏心距越大，压差增大越快，即对旋转体旋转方向的力越大。但与此同时力臂随着偏心距的增大而减小，且偏心距越大，力臂减小得越快，这也就导致了流体驱动旋转体旋转方向的转矩随着偏心距的增大而逐渐增大。

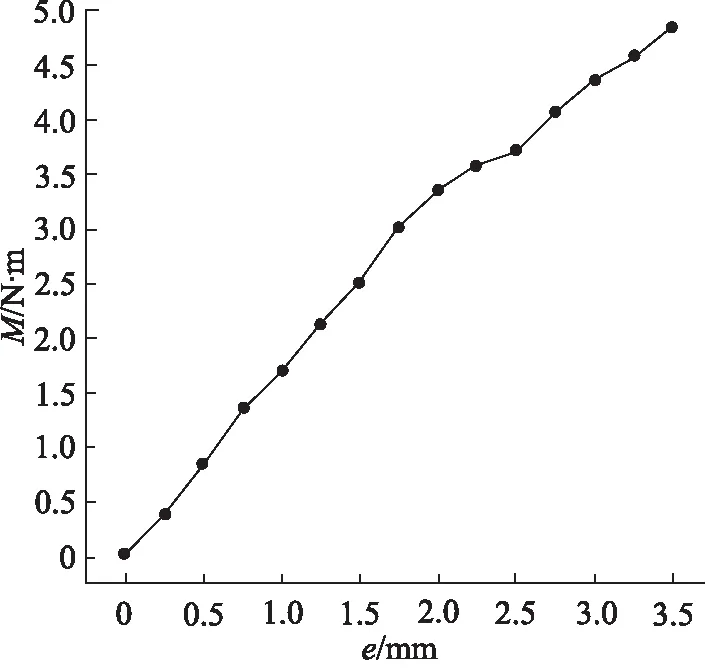
图4 不同偏心距下旋转体的转矩曲线Fig.4 Torque curve of rotating body under different eccentricities

2) 流速随斜射流口偏心距变化的规律

为直观地体现喷嘴出口流速随偏心距的变化规律，展示斜射流口偏心距e分别为0.5，1.5，2.5，3.5 mm 时斜射流口的出口流速，如图5所示。除去靠近边界层外边界的流体，截面可以明显地划分为高流速区域和低流速区域两部分。流体自中心腔室进入斜射流口后，由于具有惯性，有着朝既定流线流动的趋势。但此时流场发生突变，流体受到一侧壁面约束后转向，该侧压力急剧增大，形成高流速区域，另一侧流体具有与边界层分离的趋势，形成低流速区域。在研究范围内，随着偏心距的增大，低流速区域面积逐渐扩张，且高流速区域有着左侧外缘向下扩张，右侧外缘向上收缩的趋势。这是由于随着偏心距的增大，流体自中心腔室流入斜射流口要受由Y轴朝Z轴方向、X轴朝Z轴方向的2个锐缘斜进口的叠加影响，流体转向的趋势越来越大，压力集中区域逐渐沿左侧壁面向下转移，使得高流速左侧外缘区域向下扩张。同时，距OYZ截面较近侧壁面的边界层逐渐发生分离，使得下方低流速区域的旋涡区向右上方移动且增大，且高流速右侧外缘区域收缩，低流速区域向外扩张。

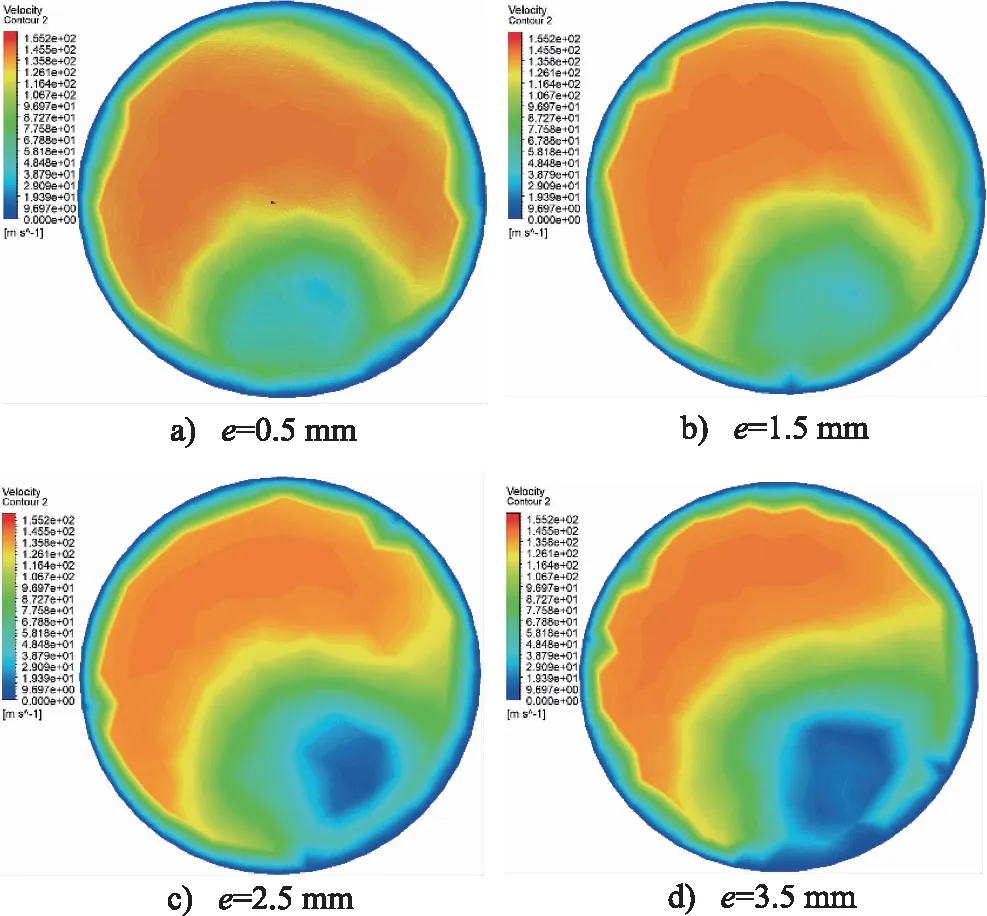
图5 变斜射流口偏心距喷嘴出口速度云图Fig.5 Velocity nephogram of variable angle jet nozzle with eccentric distance from nozzle outlet

在不改变斜射流口与水平面夹角的情况下，以0.25 mm作为间距，在0～3.5 mm之间选取15个特征值作为两斜射流口偏心距，分别建立15个不同流体域模型所产生的射流口的出口平均流速曲线，如图6所示。在研究范围内，中心射流口的出口平均流速对偏心距的变化不敏感，平均流速在(133.5±0.5)m/s之间浮动。对于斜射流口，偏心距由0 mm变为 0.25 mm 时，其平均流速下降了1.33 m/s；偏心距在0.25～1.75 mm之间时，曲线平缓，平均流速在(114.3±0.5) m/s 之间浮动；偏心距在1.75～3.5 mm之间时，曲线变陡，平均流速随着偏心距的增大逐渐减小。结合上述偏心距对壁面压力分布以及喷嘴出口速度分布影响规律来看，偏心距由0 mm变至0.25 mm后，流体流入斜射流口开始对其距OYZ截面远侧壁面冲击，部分能量用于驱动旋转体旋转，进而导致流体总水头的下降，在出口处体现为平均流速的下降。偏心距在0.25～1.75 mm之间时，作用于远侧壁面法线方向的力变化量较小，因此驱动旋转体旋转的能量变化量较小。由图5可以看出，低流速区域没有明显的变化，在该区段内斜射流口出口平均流速没有明显的变化。偏心距在1.75～3.5 mm之间时，作用于远侧壁面法线方向的力变化量增大明显，驱动旋转体旋转的能量变化量增大，同时低流速区域由于近侧壁面的边界层发生分离，使得下方低流速区域的旋涡区增大，尾流旋涡耗能显著增加，导致了在该区段平均流速随偏心距的增大而减小。

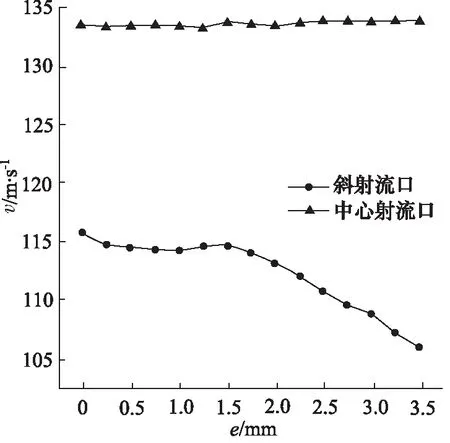
图6 不同偏心距下射流口的出口平均流速曲线Fig.6 Average velocity curve at nozzle outlet of jet tube under different eccentricities

4.2 变斜射流口与水平面夹角分析

1) 转矩随斜射流口与水平夹角变化的规律

为直观地体现喷嘴转矩随夹角的变化规律，展示偏心距e为3.5 mm，斜射流口与水平面夹角α分别为30°，40°，50°，60°时的压力分布情况，如图7所示。在研究范围内，随着水平夹角的增大，斜射流口入口处距OYZ截面较远侧壁面压力大小没有明显的变化，但其压力集中部位随着水平夹角增大而上移。距OYZ截面较近侧壁面因水平夹角的增大，从与中心腔室的侧壁面相接变为与中心腔室的下壁面相接，结构突变更加显著，使得近侧壁面边界层分离点后移，进而导致近侧壁面压力减小，说明随着水平夹角的增大，壁面压差增大。

偏心距为0.5, 1.5, 2.5, 3.5 mm的情况下，以5°作为间距，在斜射流口与水平夹角为30°～60°之间，分别选取7个特征值建立不同流体域模型的旋转体转矩M曲线，如图8所示。经仿真监测结果得，在这28个流体域模型中， 射流反推力对旋转体所产生的转矩不足流体对斜射流口壁面作用后所产生转矩的0.6%，旋转体转矩主要由斜射流口壁面压差所提供。在研究范围内，随着水平夹角的增大，转矩逐渐减小。当偏心距为0.5 mm时，转矩随着水平夹角的变化较为平缓；当偏心距为1.5，2.5，3.5 mm时，转矩随着水平夹角的增大而减小，且水平夹角越大，曲线越陡。结合图7及上述射流口水平夹角的变化导致壁面压差发生变化规律来看，虽然随着偏心距的增大，壁面压差增大，但由于两圆柱相交的几何结构特点，流体流入斜射流口后所冲击的壁面逐渐向斜上侧转移，导致作用于旋转体旋转方向的压力分量变小，同时，水平夹角的增大，也导致了其转矩力臂的减小，并且角度越大， 力臂减小得越快。这也说明了随着水平夹角的增大，转矩总体是随之减小的，且水平夹角越大，转矩减小得越快。

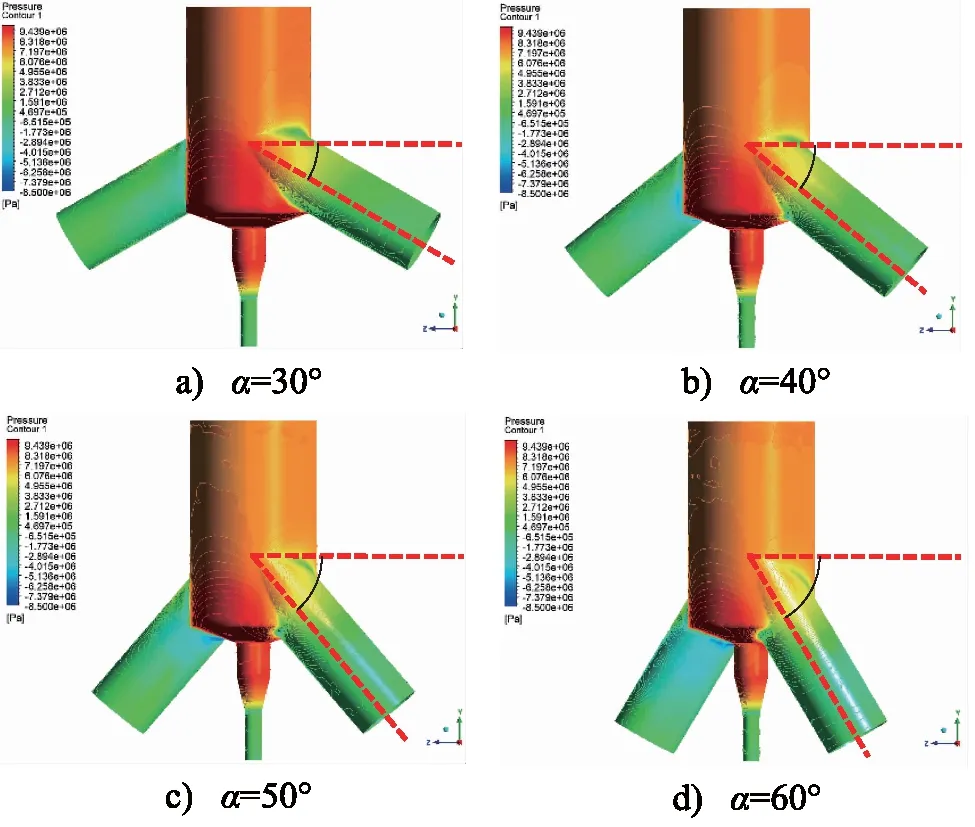
图7 变斜射流口水平夹角压力云图Fig.7 Pressure nephogram of variable angle jet nozzle

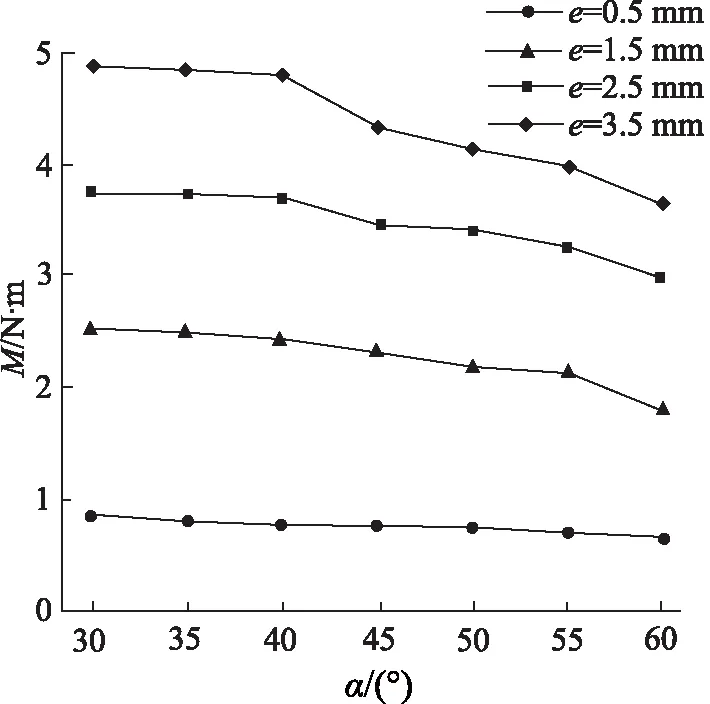
图8 不同水平夹角下旋转体的转矩曲线Fig.8 Torque curve of rotating body under different horizontal angles

2) 流速随斜射流口与水平夹角变化的规律

为直观地体现喷嘴出口流速随偏心距的变化规律，展示偏心距e为3.5 mm，斜射流口与水平夹角α分别为30°， 40°， 50°， 60°时斜射流口出口流速，如图9所示。除去靠近边界层外边界的流体，截面可以明显地划分为高流速区域和低流速区域两部分。在研究范围内，低流速区域面积随着水平夹角的增大而减小，且逐渐朝右上方移动，水平夹角由30°变为40°时，流体从Y轴方向朝Z轴方向的锐缘斜进口转角变小，斜射流口下壁面开始与中心腔室下壁面相交，流场下侧局部阻碍变小，下壁面边界层不发生分离，压力集中区域逐渐沿左侧壁面向下扩张，旋涡区显著变小。水平夹角由40°向后逐渐增大的过程中，近侧壁面与中心腔室下壁面的交线变长，近侧壁面的边界层发生分离，旋涡区又逐渐增大且向右上方移动。

图9 变斜射流口水平夹角喷嘴出口速度云图Fig.9 Velocity nephogram of nozzle outlet with horizontal angle of variable angle jet nozzle

偏心距分为0.5，1.5，2.5，3.5 mm的情况下，以5°作为间距，在斜射流口与水平夹角为30°～60°之间，分别选取7个特征值建立不同流体域模型的两射流口的出口平均流速曲线，如图10所示。在研究范围内，中心射流口的出口平均流速对水平夹角的变化不敏感，平均流速在(133.5±0.5) m/s之间浮动；对于斜射流口，曲线整体呈现为先上升后下降的趋势。结合图7、图9来看，随着水平夹角的增大，斜射流口的下壁面与中心腔室下壁面交线变长，沿Y轴方向朝Z轴方向的锐缘斜进口转角变小，边界层分离点前移，直至边界层不发生分离，流场下侧的旋涡区越来越小直至消失，导致其尾流旋涡耗能显著减小，对流速产生正影响。而斜射流口近侧壁面与中心腔室下壁面交线变长，沿X轴方向朝Z轴方向的锐缘斜进口转角变大，近侧壁面的边界层发生分离，旋涡区又逐渐变大，导致其尾流旋涡耗能增大，对流速产生负影响。因此，在研究范围内，斜射流口出口平均流速随着水平夹角的增大呈现先增大后减小的趋势，且随着偏心距的增大其平均流速峰值点逐渐后移。

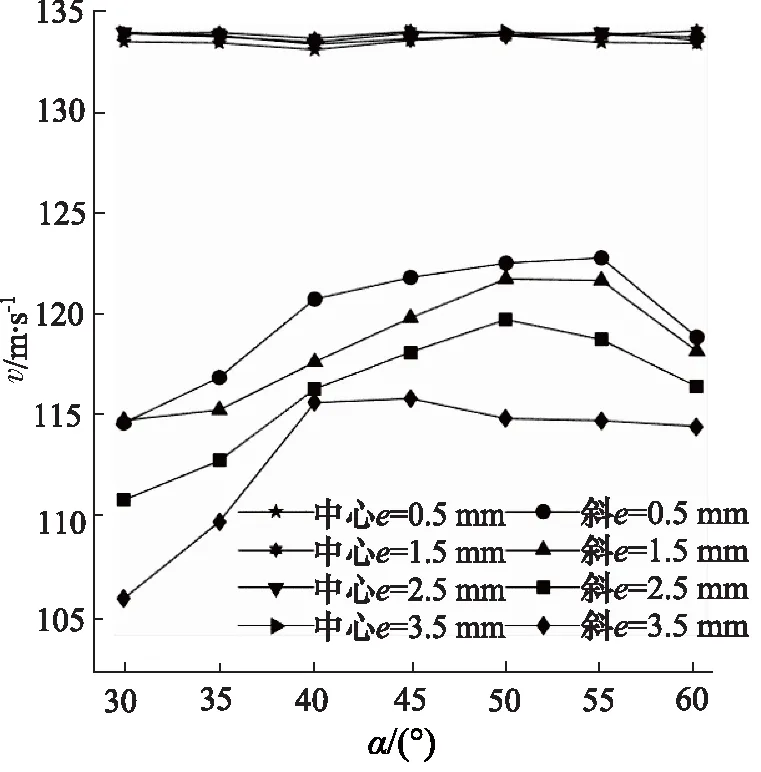
图10 不同水平夹角下射流口的出口平均流速曲线Fig.10 Average velocity curve of jet outlet under different horizontal angles

5 结论

本研究应用数值模拟的方法对新型钢板桩液力自旋式喷嘴进行了流体仿真研究，得到如下结论：

(1) 在研究范围内，射流反推力对旋转体所产生的转矩不足流体对斜射流口壁面作用后所产生的转矩的0.6%，转矩主要由斜射流口壁面压力差提供；中心射流口的出口流速对偏心距和水平夹角的变化不敏感，平均流速在(133.5±0.5) m/s之间浮动；

(2) 随着偏心距的增大，斜射流口壁面的压差增大，且偏心距越大，压差增大得越快，与此同时力臂随着偏心距的增大而减小，且偏心距越大，力臂减小得越快，在两因素的影响下，旋转体的转矩随着偏心距的增大而稳步增大；偏心距在0～0.25 mm之间时，其平均流速下降了1.33 m/s；偏心距在0.25～1.75 mm之间时，平均流速变化平缓；偏心距在1.75～3.5 mm之间时，平均流速随着偏心距的增大稳步减小；

(3) 随着偏心距的增大，斜射流口壁面压差增大，但由于两圆柱相交时的几何结构特点，流体流入斜射流口后冲击的壁面逐渐向斜上侧转移，导致作用于旋转体旋转方向的压力分量减小，与此同时力臂随着偏心距的增大而减小，并且角度越大，力臂减小得越快，在两因素的影响下，随着水平夹角的增大，转矩总体随之减小，且水平夹角越大，转矩减小得越快；受下壁面和近侧壁面尾流涡流耗能的影响，斜射流口的出口平均流速随着水平夹角的增大呈现先增大后减小的趋势，且随着偏心距的增大其平均流速峰值点逐渐后移。

本研究对新型钢板桩液力自旋式喷嘴进行设计和仿真研究，为下一步水射流研究奠定了基础，并为该喷嘴结构优化提供了参考依据。