气动肌肉关节的刚度分析及变刚度运动控制

2022-09-20王悠草周祎博崔小红王斌锐

液压与气动 2022年9期

王悠草，周祎博，崔小红，周坤，王斌锐

(中国计量大学机电工程学院，浙江杭州 310018)

引言

智能仿生机器人是目前极具潜力的方向，常用于仿生机器人的气动肌肉驱动器能较好模仿肌肉运动[1]，具有类人肌肉变刚度优势，其定位及柔顺性的准确控制是人机协作中最重要的规范[2]。气动肌肉克服液压驱动中液体压缩困难问题[3]，可模仿人体肌肉从软到硬的变刚度特性，通过适度收缩发力，使肢体到达预设角度。气动肌肉仿生机器人对非结构化环境适应力强，安全性高，角度控制无需非常精确，运动接触更多靠关节柔性完成。而仿生腿式机器人的关节是运动的核心，合理规划关节刚度是实现平稳摆动和软着陆的关键。

目前，气动肌肉关节的变刚度运动控制问题重点集中在机构运动刚度特性和主动变刚度控制算法2个层面。为使气动肌肉仿生机器人在运动过程中刚度可控，实现其“僵化危险”到“灵活类人”的跨越，众多研究者在以下两方面进行相关研究：

(1) 在气动肌肉自身刚度特性层面，国内外有较多研究[4-5]。CHEN等[6]提出拮抗气动肌肉驱动器可在长度不变下调节刚度，并进行多组长度下刚度实验，探索不同刚度能力。SOLEYMANI等[7]基于限制链可扩展性理论，开发了一种基于连续力学的气动肌肉新模型，以预测驱动过程中的刚度和输出参数。从控制主动性角度分析，上述研究可归为被动刚度特性，尽管存在诸多缺陷，但为刚度控制基础，可衍生多种控制效果。

(2) 在主动变刚度控制算法层面，现有研究可归为4类方法： ① 设计气动肌肉新模型。ZHAO等[8]建立气动肌肉等效变刚度弹簧模型，设计相应双入双出滑模控制器，仅达到角度开放下刚度控制； ② 设计特定机器人结构。LIU等[9]用细径气动肌肉控制内外肌肉开发刚度连续可控的操作臂，沈双等[10]设计气动肌肉与弹簧对拉的串联弹性关节实现角度/刚度控制，但均非人体关节的拮抗肌肉结构，运动不够高效； ③ 设计新算法控制结构。TARO等[11]将估计刚度加入力矩控制, 实现机械平衡模型的直纤维型人工肌肉手关节刚度/角度控制；YAMAMOTO等[12]使用模型误差补偿器(MEC)设计角度、气压和刚度控制器，由多MEC回路实现气肌手臂角度/刚度控制；UGURLU等[13]提出一种新型控制器结构, 实现肌肉关节转矩/刚度和角度/刚度两种控制模式； ④ 设计角度/刚度的气压解算模型。朱坚民等[14-15]根据力矩/刚度与气压关系，建立拮抗气动肌肉仿生关节气压解算模型，用此模型实现刚度开环、角度闭环的控制实验。总体看来，方法IV更为直观、控制简单且适用于类人关节结构，但现有气动肌肉关节控制效果尚待提高，需研究易实现、高精度、控制能量少的角度/刚度双环控制算法。

本研究结合上述2个层面，分析气动肌肉仿生腿摆动下单根肌肉及髋、膝关节的刚度变化特性。在变刚度运动控制层面，在方法④基础上以计算力矩法输出力矩项替换原有力矩控制量，设计采用含力矩项补偿气压解算模型的角度/刚度双闭环控制算法。搭建仿真及实验平台，通过对比分析，验证所提算法可实现高精度角度/刚度控制。

1 气动肌肉仿生腿刚度特性分析

1.1 仿生腿模型及计算力矩串级角度控制法

仿生腿[16]由躯干、大腿和小腿组成，运动模型如图1。θh和θk表示髋、膝关节角度，r为圆形转轮半径，τh为髋关节力矩，τk为膝关节力矩。Mi表示气动肌肉，Fi和xi为气动肌肉轴向拉力和末端位移，下标i=a，b，c，d表示不同角度。图1中，Ma, Mb为长185 mm 自制气动肌肉，Mc， Md分别为长133 mm， 156 mm 自制气动肌肉。

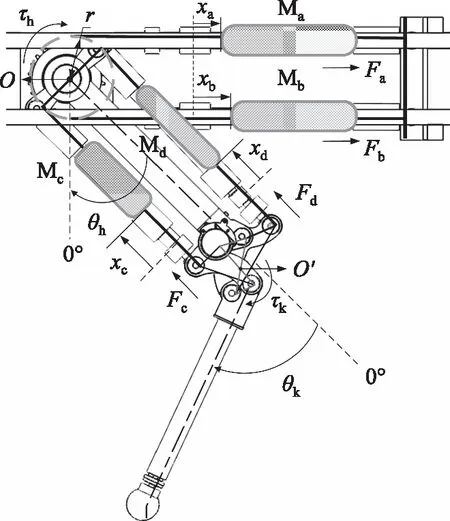
图1 仿生腿运动模型Fig.1 Bionic leg motion model

以顺时针为正方向，角度范围由弧度值表示，髋关节角度θh(θh∈[-1.22,-0.35])与拮抗肌肉Ma，Mb位移xa，xb的数学关系分别为：

xa=(θh+1.22)·r

(1)

xb=(-θh-0.35)·r

(2)

髋关节驱动力矩τh与拮抗肌肉Ma，Mb各自拉力Fa和Fb关系为：

τh=(Fa-Fb)r

(3)

式中，τh为在拉力Fa和Fb对图1中O点施加的髋关节力矩，设计髋关节力矩τh到两根气动肌肉Ma， Mb各自拉力Fa，Fb的数学映射关系[16]，得单根肌肉理论拉力值。

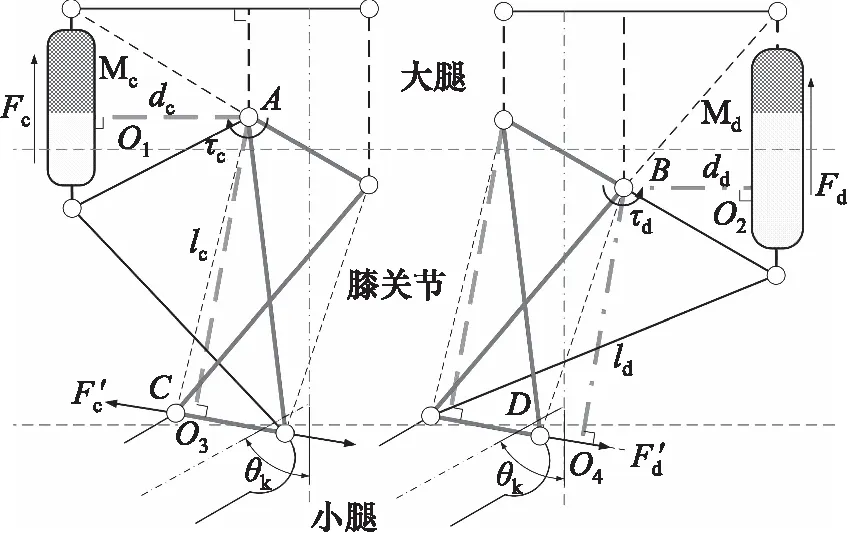
图2 膝关节运动学模型与力矩示意图Fig.2 Knee motion model and torque schematic diagram

(4)

(5)

图2中，τc和τd是拉力Fc，Fd对A，B点施加的力矩。静力学平衡方程为：

(6)

(7)

ctau=τc/τd=lc/ld

(8)

绕四连杆瞬心转动的膝关节驱动力矩τk为：

τk=τc-τdctau=Fcdc-Fdddctau

(9)

单腿摆动角度控制算法采用双闭环计算力矩控制策略，由角度外环和拉力内环组成。角度外环控制器输出控制力矩τci由PI控制器求取并引入单腿动力学计算力矩τfi，两者之和为给定力矩τri。

图3中，xi为肌肉收缩量，期望角度θr=[θhrθkr]T，θhr为髋关节期望角度，θkr为膝关节期望角度，实际角度θ=[θhθk]T。给定拉力Fgi由控制力矩τri和关节转角θ映射得到、单腿动力学计算力矩、单腿动力学模型可由拉格朗日动力学求得[16]。因气动肌肉有效工作状态仅在低频率，故气动肌肉三元素模型[17]中阻尼单元阻尼系数较小可忽略，可等效为收缩单元加弹簧单元并联的两元素模型，拉力为：

Fi=Zi-Kixi

(10)

式中，Fi为肌肉拉力，Zi为收缩单元收缩力，Ki为刚度单元刚度。气动肌肉在0.1 MPa下的的气压-收缩力、气压-刚度关系写为通式，有：

(11)

式中，下标i=a，b，c，d为不同肌肉位置；c1i，c2i，v1i，v2i，v3i，v4i为数字常量；pi为肌肉内部充气气压；pdi为不同分段点数值。联立式(10)与式(11)，得气动肌肉逆模型解算的气压前馈控制器的输出为：

(12)

式中，p1i=(Fgi+v2ixi-c2i)/(c1i-v1ixi)，

p2i=(Fgi+v4ixi-c2i)/(c1i-v3ixi)，

pfi为控制器前馈气压值;p1i,p2i为气压中间变量。Fgi为气动肌肉给定拉力。拉力控制器叠加拉力误差经PI控制器的输出得到给定气压pri。拉力PI控制器输出控制气压pci如下：

(13)

式中，kpi，kii为比例及积分系数。

则叠加后的拉力控制器输出给定气压：

pri=pfi+pci

(14)

给定气压pri经调压比例阀气压转电压线性常系数kpu后，得拉力控制器输出。

1.2 仿生腿肌肉及关节刚度特性

在运动科学领域中，研究下肢的“刚度”这一机械特性对下肢多关节任务(如走、跑、跳等)至关重要[18-19]。首先，通过对3种不同长度规格气动肌肉分别做等压特性实验辨识获得式(11)中具体系数，共得到长度为185 mm的Ma和Mb、133 mm的Mc、156 mm的Md，三者在0.1 MPa气压-收缩力、气压-刚度关系分别为：

(15)

(16)

(17)

式中，Zi(i=a,b)为肌肉Ma, Mb收缩单元收缩力，Ki(i=a,b) 为肌肉Ma, Mb刚度单元刚度。Zc,Zd为肌肉Mc, Md收缩力，Kc,Kd为肌肉Mc, Md刚度。单根气动肌肉刚度由三元素模型中刚度单元表示。气动肌肉关节刚度定义为K=-dτ/dθ，即力矩与转角比。由式(10)知，肌肉Ma, Mb单根拉力为：

式中，i=a,b，xi由式(1)、式(2)求得。

髋关节刚度为：

(19)

式中,

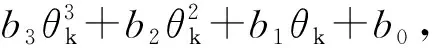
气动肌肉Mc, Md拉力为:

(20)

(21)

式中，xc,xd由式(4)、式(5)求得。

膝关节刚度Kk为:

(22)

1.3 仿生腿肌肉及关节被动刚度分析

在仿真软件MATLAB/Simulink中分析仿生腿以周期T=8π/3及T=2π摆动下气动肌肉及关节整体刚度变化，结果如图4所示。当气动肌肉仿生腿摆动2 s稳定后，将仿真曲线中气动肌肉Ma, Mb, Mc, Md及髋、膝关节每部分的刚度变化范围记录为表1。

表1 两种摆动周期下各部位刚度变化范围Tab.1 Stiffness variation range of each part under two frequency swing

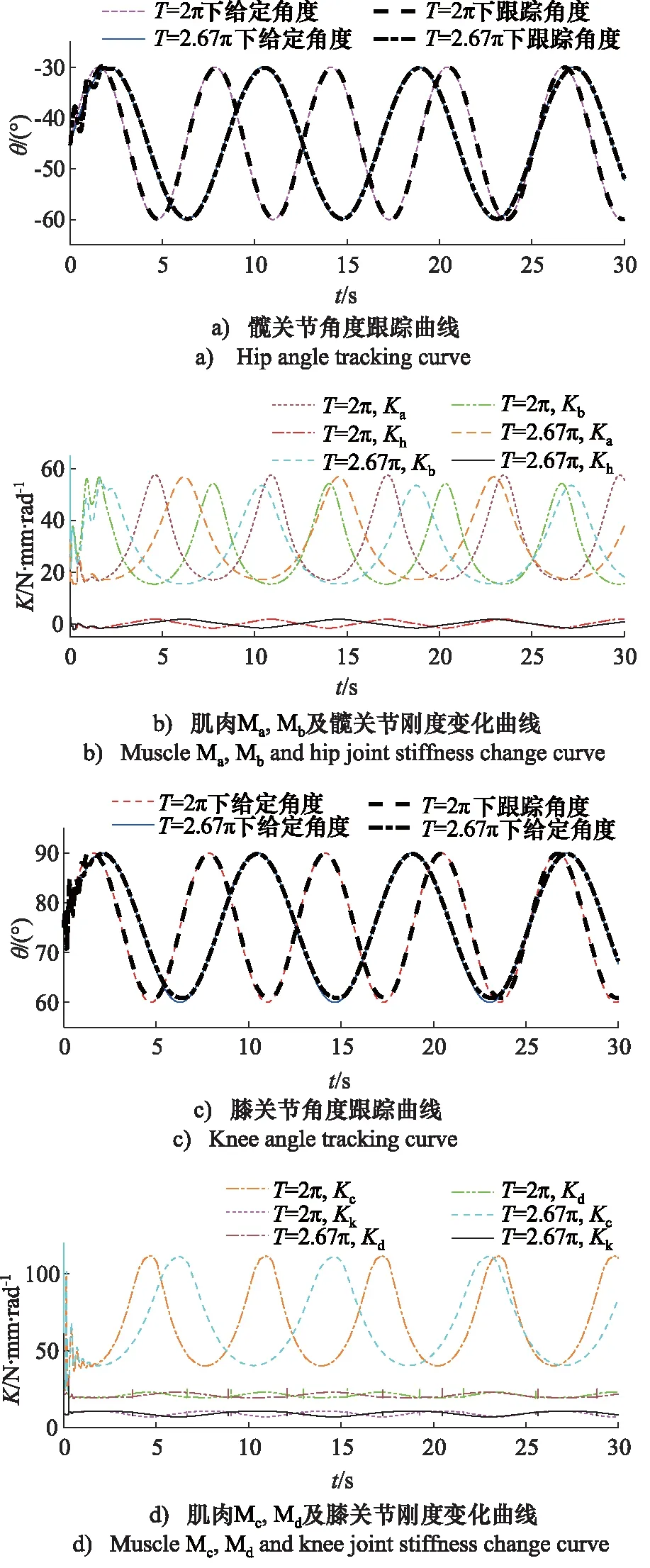
图4 仿生腿两种摆动周期下角度跟踪及刚度变化曲线Fig.4 Angle tracking and stiffness change curves of bionic leg under two cycle of swing

基于计算力矩控制的双环级联角度控制算法中，仿生腿上每根肌肉理论气压结算结果固定，而刚度与角度均与气压有关，分析图4及表1可得：

当摆速大时，单根肌肉刚度及关节整体刚度上限更高、下限更低、变化范围大，同时代表更强的运动能力。因髋、膝关节半径远小1 m，短距离作用下，关节整体刚度远小于单根气动肌肉刚度。

仿生腿摆动时，两组拮抗气动肌肉共同作用克服腿重力。圆形转轮结构的髋关节上2根气动肌肉Ma, Mb刚度大小交替变化，四连杆变转轴结构构成的膝关节上两根气动肌肉Mc和Md刚度同步变化，156 mm规格气动肌肉Md刚度变化不大，运动效果主要由133 mm 规格气动肌肉Mc刚度变化带动。关节角度与刚度同期达到极值且当髋、膝关节转动角以正弦波形式变化下，单根气动肌肉刚度及关节刚度亦以正弦波形式变化。

2 膝关节基本模型双环法设计

目前把下肢刚度变化特性应用于可变刚度仿生机器人的研究尚鲜有涉足，而膝关节主要影响机器人高承载下奔跑等复杂运动。本研究以膝关节为控制对象，研究关节位置/刚度同步控制方法，为实现仿生足式机器人复杂场景下运动控制奠定基础。

2.1 膝关节动力学建模

单腿机构简化模型可视为平面连杆机构，腰部及大腿固定，由拉格朗日动力学建模定理[20]，建立膝关节单摆动力学方程为:

(23)

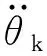
表2 膝关节控制系统物理参数Tab.2 Physical parameters of knee joint control system

2.2 角度/刚度控制基本模型双环法原理

气动肌肉Mc， Md在内部充气气压作用下可得唯一膝关节角度θk和关节刚度K。故控制关节角度及刚度需由预期角度θkr及预期刚度Kr解算出2根气动肌肉理论充气气压pc,pd。

图1中膝关节转动中心点O′的转角角度与刚度为被控量。控制系统两个输入为膝关节预期角度θkr与预期刚度Kr，目标是预期变化刚度下膝关节轨迹随动跟踪，即角度/刚度双闭环控制，原理图如图5所示。膝关节数学模型由气动肌肉Mc,Md模型、膝关节运动学模型、动力学模型和输出刚度计算模型4部分组成。输入为pc,pd，输出为膝关节实际角度θk和实际刚度K。膝关节角度/刚度气压解算模型的输入是控制算法双PID的输出量uk，uθ，输出为pc,pd。

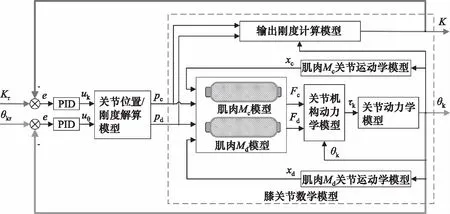
图5 基本模型双环法控制框图Fig.5 Basic model doubleloop method block diagram

膝关节角度和刚度为被控量。ek，eθ为实时控制时关节实际角度θk和周期角度θkr、膝关节实际刚度K与期望刚度Kr的控制偏差，经PID算法产生控制量输出uθ，uk，经关节角度/刚度气压解算模型实时计算出两根肌肉充气压力pc，pd。再经运动学模型解算出气动肌肉Mc, Md压缩量xc，xd，通过肌肉数学模型求解肌肉各自拉力Fc,Fd驱动膝关节转动。Fc,Fd经2个动力学模型求得实际角度θk，构成角度闭环；另外，pc,pd与膝关节角度经关节刚度计算模型求得输出刚度K，构成刚度闭环。

图5控制框图共由气动肌肉Mc, Md模型、关节动力学模型、运动学模型、输出刚度计算模型、气压解算模型等部分构成：

(1) 肌肉模型膝关节两根肌肉模型如式(20)、式(21)所示；

(2) 动力学模型对仿生腿膝关节四连杆进行受力分析，得关节机构动力学模型为式(26), 由拉格朗日动力学建模法，得气动肌肉仿生腿膝关节动力学模型式(23)；

(3) 运动学模型膝关节的运动学模型式如式(4)、式(5)所示；

(4) 输出刚度模型记膝关节刚度为K，由关节整体刚度计算式，可得膝关节输出刚度计算模型为式(31)；

(5) 气压解算模型膝关节的角度/刚度控制需要根据期望角度、期望刚度反解出两充气气压，膝关节驱动力矩τk和输出刚度K均是关于两气压pc,pd的函数，两充气气压由此直接解算。

因气动肌肉的拉力拟合模型是关于气压的分段函数，角度/刚度同时控制气压求解模型解算过程过于繁琐，为控制简便，气动肌肉模型采用由能量守恒原理、虚功原理所建理想数学模型[21]。

Fi=pi[a(1-εi)2-b]，i=c, d

(24)

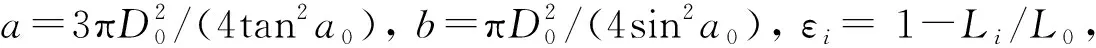
考虑重力作用且在静力学平衡条件下，小腿绕四连杆瞬心转动的驱动力矩：

τk=mglmsinθk+Fcdc-Fdddlc/ld

(25)

膝关节可变力臂由图2反余弦等数学关系解算出，形式繁琐，为简化求解及后续求导过程，可忽略四连杆运动中机构形状变化对力臂的影响，即dc=ddlc/ld=r1，再将式(24)代入式(25)，可得膝关节驱动力矩：

τk=mglmsinθk+Fcr1-Fdr1

=mglmsinθk+pc[a(1-εc)2-b]r1-

pd[a(1-εd)2-b]r1

(26)

从膝关节四连杆变转轴机构活动半径计算简便考虑，四连杆可简化为圆形转轮(r1=0.03 m)结构。以顺时针为正，角度范围由弧度值表示，膝关节角度θk(θk∈[0,1.57])，则膝关节上两根气动肌肉Lc,Ld长度分别为：

Lc=L0c-θ·r1

(27)

Ld=L0d-(1.57+θ)·r1

(28)

式中，L0c,L0d为肌肉Mc, Md原长0.133 m和0.156 m。由式(26)链式求导法则，膝关节输出刚度：

(29)

式中，dFc/dLc与dFd/dLd, dLc/dθ, dLd/dθ可由式(24) 、式(27)、式(28)分别求导得到：

(30)

将式(30)代入式(29)，可得膝关节输出刚度：

(31)

在期望角度θkr与期望刚度Kr已知情况下，联立式(26)、式(31)，可得气压解算模型为：

(32)

式中，φd,φc,ψd,ψc,uθ,uk分别为：

式(32)可由期望位置θkr与期望刚度Kr解算出气压pd，pc通过不同进气管及比例阀分别独立控制，说明图5膝关节基本模型双环法对角度/刚度控制原理的可行性。

3 力矩项补偿模型双环法设计

考虑基本模型双环法属于传统负反馈控制方法，对于气动肌肉仿生腿机器人这类强耦合、非线性系统控制精度不高，参数调节过程较长且很难实现完全解耦，而若采取智能控制算法[22]需充分考虑计算繁琐、抖振等代价，且可能造成系统稳定性方面影响。

为满足膝关节角度/刚度同时高精度控制要求，本研究基于计算力矩加PD反馈控制算法对非线性被控对象的高度补偿性，在图5含基本气压解算模型控制框的基础上，将角度闭环采用计算力矩控制加PD反馈算法[23]得到控制力矩项，替代式(21)和式(26)两式联立所需力矩，用改进后的力矩项补偿气压解算模型替代原有模型，能更接近被控对象物理系统的真实解算模型数值，力矩项补偿模型双环法的控制原理框图如图6所示。

图6力矩项补偿模型双环法新增的逆动力学模型式为：

(33)

(34)

式中，φd，φc，ψd，ψc，τkr，uk分别为：

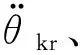
图6 力矩项补偿模型双环法框图Fig.6 Torque item compensation model double loop method block diagram

4 仿真测试与结果分析

在MATLAB/Simulink软件环境下，根据基本模型双环法、力矩项补偿模型双环法设计轨迹及刚度跟踪控制器，以仿真膝关节动态轨迹及刚度跟踪情况，研究不同模型下双环法对膝关节角度/刚度二者的控制精度影响。刚度实时数值由调压比例阀实时数值及角度编码器实时数值经式(28)计算出。

基于多次调试得到的较优控制参数，两种算法仿真结果如图7所示，分别表示两种模型双环法下，仿生膝关节位置跟踪及误差Δθk曲线、仿生膝关节刚度跟踪及误差ΔKk曲线。可见两种控制算法对关节角度/刚度均达到较理想控制效果，仿真得到的数据统计结果见表3。

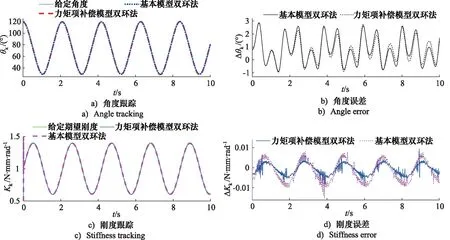
图7 两种算法下膝关节角度/刚度控制仿真曲线Fig.7 Diagram of knee angle/stiffness control simulation curve under two algorithms

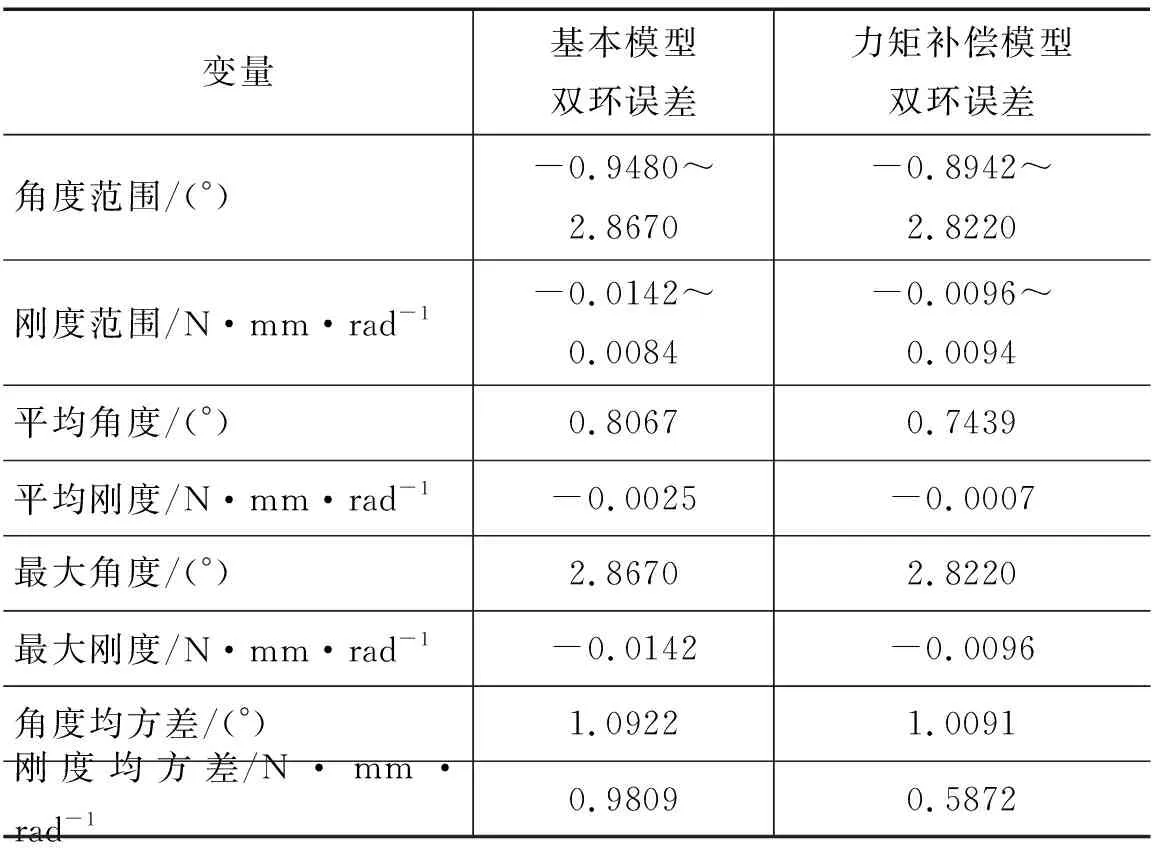
表3 力矩项补偿模型双环法和基本模型双环法仿真比较Tab.3 Simulation comparison between torque compensation model double loop method and basic model double loop method

位置控制方面，设置期望关节位置曲线为30°～120°的正弦曲线，关节位置仿真结果可见，力矩项补偿模型双环法跟踪误差最大幅值、平均误差、均方差均优于基本模型双环法。由最大误差可求得位置控制精度提高了约3%。

刚度控制方面，设置期望关节刚度曲线为0.6～1.4 N·mm/rad的正弦曲线，关节刚度仿真结果可见，力矩项补偿模型双环法跟踪误差最大幅值、平均误差、均方差均优于基本模型双环法。由最大误差可求得刚度控制精度提高了约32%。

5 实验与结果分析

本研究气动肌肉仿生腿样机实验平台为自主研发，仿生腿悬挂固定竖直导轨，气动调压比例阀安装在铝型材上，与导轨固定。实验平台如图8所示，含Beckhoff嵌入式控制器(CX2040)、角度编码器(CHA38S6-12B-GDC24R1S1)、气动比例阀(SMC ITV2050-212N)、空气压缩机、PC机等，控制算法基于TwinCAT3软件平台利用PLC与C++编程。

图8 仿生腿实验平台Fig.8 Bionic leg experimental platform

首先设置气动肌肉仿生腿样机平台的膝关节给定目标角度为30°～120°正弦曲线，目标刚度设为0.6～1.4 N·mm/rad正弦曲线。为保证仅膝关节摆动，膝关节以上的大腿气动肌肉始终充入恒定气压0.55 MPa保持为较大刚度的充盈状态。膝关节角度由角度编码器测量四连杆一个定轴的转动角度间接得到。考虑数学模型是对装置物理性质的近似，实际实验中不可避免模型不准确对控制效果的影响，参数调试较理想仿真更为复杂，因此在实际实验中需要通过不断地调试刚度环PD参数和角度环PID参数，最终获得较为理想的跟踪效果。实验中控制器参数为反复调整确定的较优控制参数，实验结果如图9及表4所示。

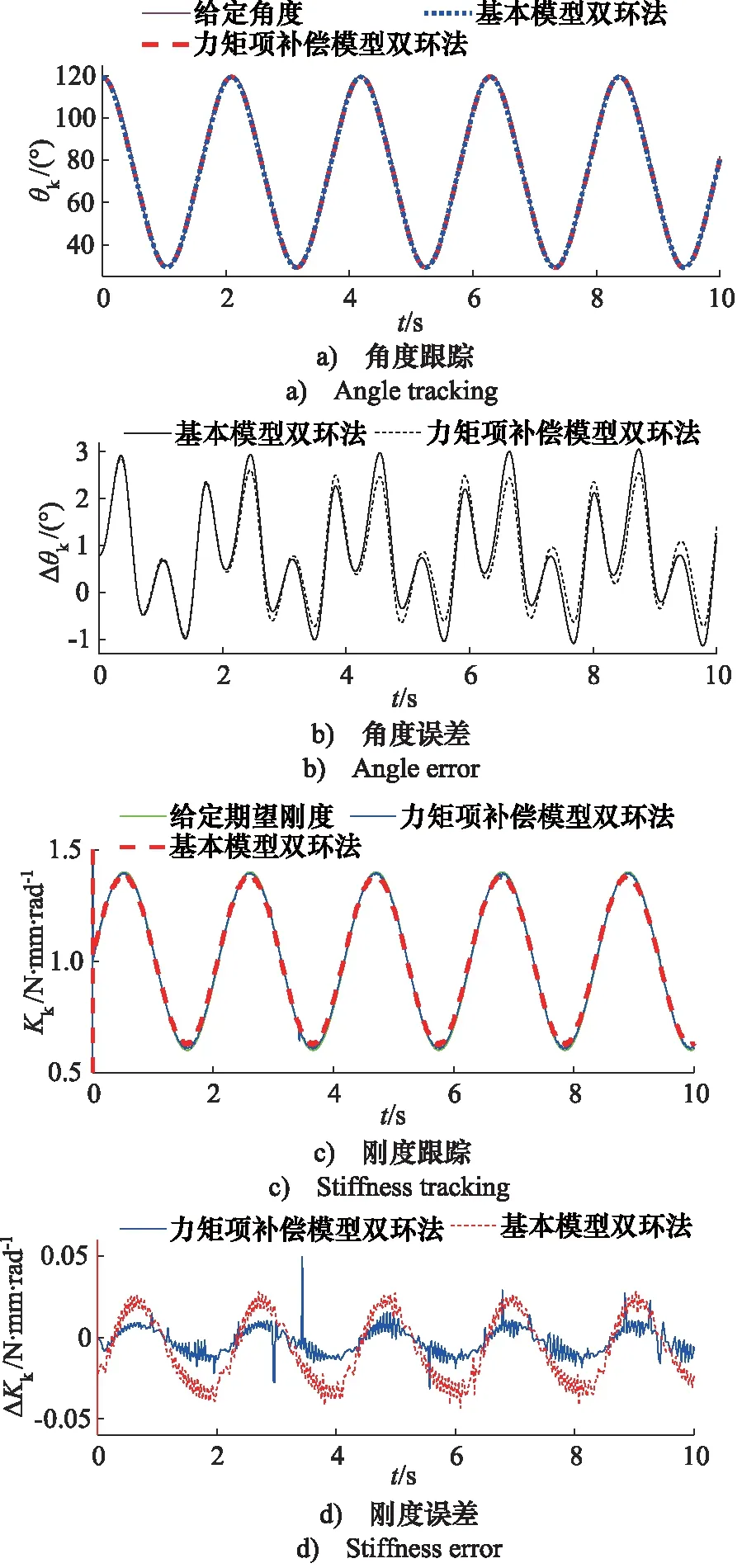
图9 两种算法下膝关节角度/刚度控制实验曲线Fig.9 Experimental curve of knee joint angle/stiffness control under two algorithms

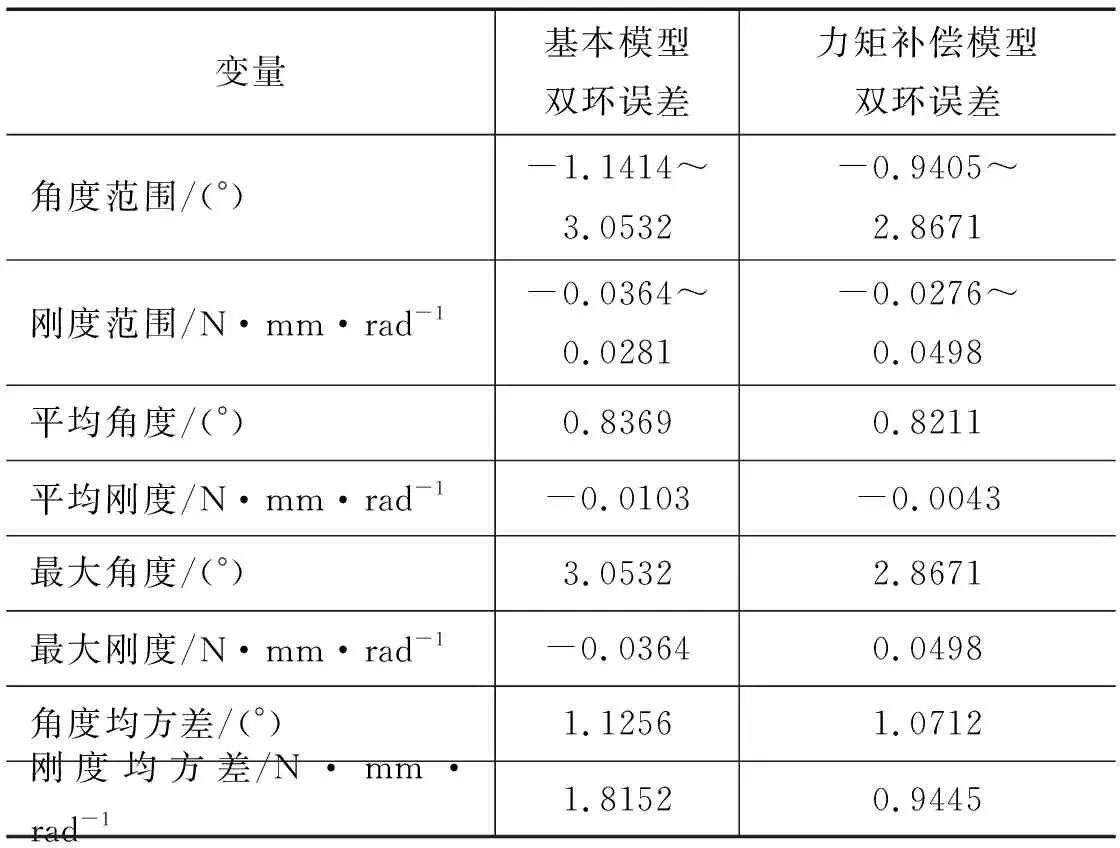
表4 力矩项补偿模型双环法和基本模型双环法实验比较Tab.4 Experimental comparison between torque term compensation model double loop method and basic model double loop method

由膝关节角度/刚度控制实验结果可见，力矩项补偿模型双环法角度跟踪误差最大幅值、平均误差、均方差均优于基本模型双环法。但力矩项补偿模型双环法在实际对膝关节刚度控制过程中，有明显尖峰出现，运动不够平滑。

仿生腿在实际摆动过程中，受各类环境因素影响，控制效果较仿真有所降低。分析原因有：一方面该技术是以完全忽略动态项这一假设为前提，会带来由非完全补偿造成的敏感性、鲁棒性问题。四连杆膝关节静态模型比拮抗定转轴模型复杂，且未考虑四连杆多转轴的静态摩擦项和动态摩擦项等，使实验中控制模型没有全面反应膝关节动态特性，且存在动力学参数估计误差和干扰项；另一方面受限于样机本体机构在实验环境中无法避免的阻尼、肌肉弹性变形及强迟滞、蠕变被控对象在拟合实验中建模误差存在，以及机构动力学模型参数很难准确，使得计算力矩控制对非线性对象的补偿效果有所削弱，故力矩项补偿模型双环法对膝关节的角度/刚度跟踪效果展示出小幅优势。