基于数形结合思想的中考考题探析——以福建省2017-2022 年近六年中考题为例

欧阳玮媛 郑秋月

（1.漳州第一中学，福建 漳州 363000；2.漳州市第八中学，福建 漳州 363000）

根据《福建省“十三五”教育发展专项规划》，2017 年起福建省中考数学由各地市自主命题转为全省统一命题。数学思想方法是全面地、笼统地讨论“what to do，how to do，why do it such”［1］。本文对福建省2017-2022 年内的中考数学试题基于数学思想方法的视角进行梳理与分析，福建省中考对数学思想方法的考查体现为应用性和综合性，即一道题考查多种思想方法，一种思想方法在不同的知识点进行考查；再基于数形结合思想视角对题目进行分析与审视，提出试题背后渗透的数形结合思想。

一、问题的提出

“双减”政策下，中考数学不再是追求难度和计算量，而是更加注重考查学生对于思想方法的理解与应用，有些题目不用计算，根据图象就可以获取很多解题关键信息。历年来，福建省中考重视对数学思想方法的考查（如表1）。而在一道题中考查多种数学思想方法大都以数形结合思想为基础，这就要求学生需要有扎实的数学基础，了解和掌握数形结合思想方法，形成快速有效的解题策略。本文通过分析中考试题，探究导致学生学习困境的原因，为中考备考及教与学提出建议。

数形结合思想主要出现在利润最值问题、对称性问题、求函数表达式问题、几何问题四大题型中，学生对这四大题型常常感到无从下手，导致得分率不高，主要问题是在只知道运用计算的方法算出结果，写不出必要的文字说明或者是出现漏解、错解，在知识点的学习过程中停留在一知半解的状态，知道结论却不知道掌握其图象进行数形结合分析，究其根本原因是学生没有意识到数形结合思想的重要性，不会运用数形结合思想，也反映出在学习和教学过程中有效渗透数形结合思想的重要性。

文章对福建省近6 年来数学中考中的四大题型进行分析，选取典例分析其中蕴含的数形结合思想以及学生常见的处理问题的误区，强调数形结合思想的重要性，进一步分析在教学过程中如何利用数形结合思想深度挖掘问题，有效提高学生分析、解决问题的能力。

二、数形结合思想渗透贯穿于数学中考

通过对福建省2022 年中考25 道真题分析可知（如表2），数形结合思想贯穿始终（除第3、7、17、19题外），是最普遍、最利于解题的基础性思维，是数学学习的一种重要视角，是解决数学问题的重要抓手，是数学核心素养的一部分［2］。

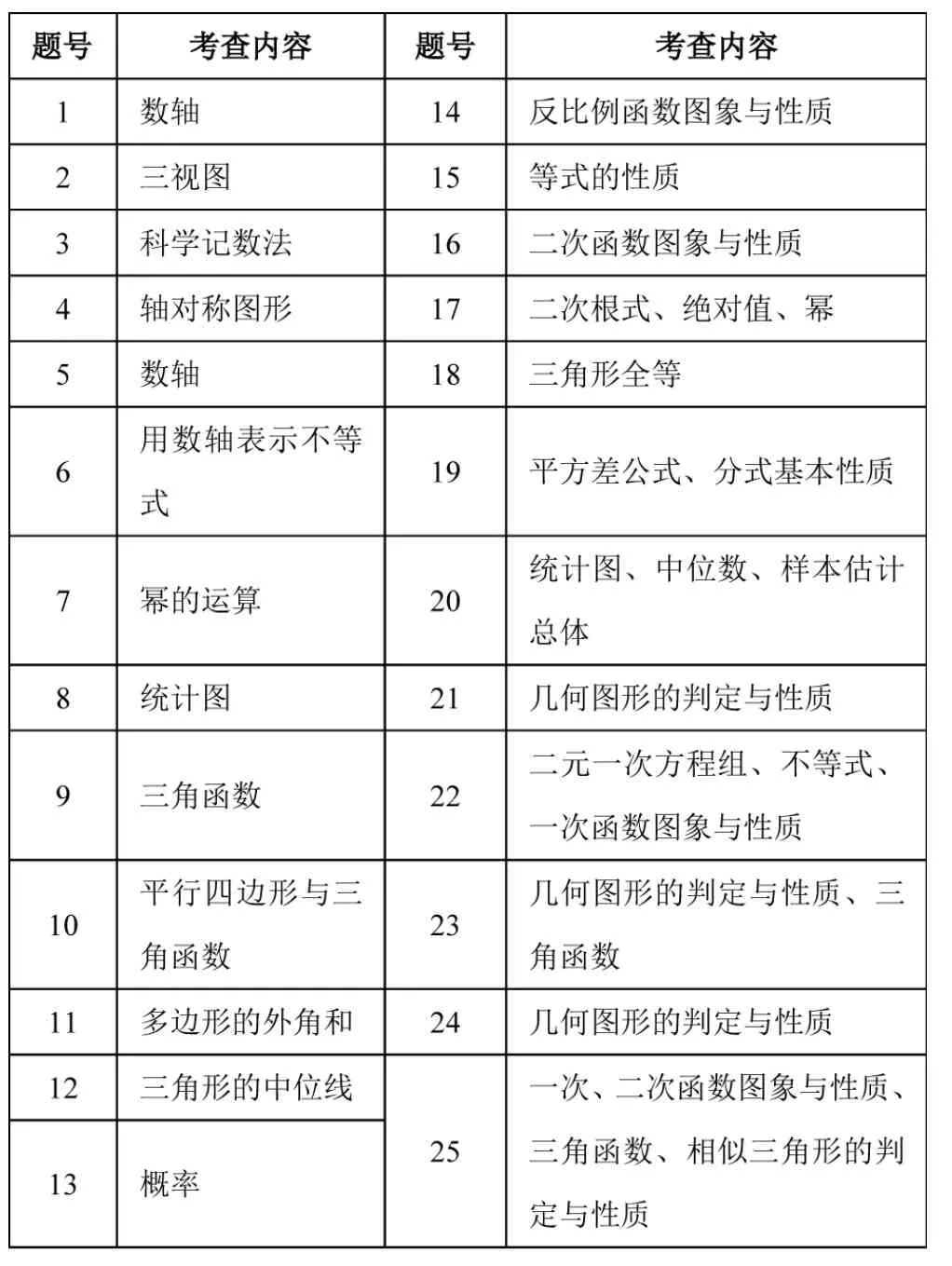
表2 2022 年福建省中考数学真题

三、福建省2017-2022 年中考典例解析

通过对福建省2017-2022 年中考试题中数形结合思想方法的分析与研究，结合中考热点问题，进一步探究如何在平时的教学过程以及中考数学总复习中有效渗透数形结合思想，扎实学生数学基础，提升学生灵活运用数形结合思想方法解决问题的能力。

（一）利润最值问题

案例1：（2022 年福建省中考数学试卷第22 题）在学校开展”劳动创造美好生活“主题系列活动中，八年级（1）版负责校园某绿化角的设计、种植与养护。同学们约定没人养护一盆绿植，计划购买绿萝和吊兰两种绿植共46 盆，且绿萝盆数不少于吊兰盆数的2 倍。已知绿萝每盆9 元，吊兰每盆6 元。

（1）采购组计划将预算经费390 元全部用于购买绿萝和吊兰，问可购买绿萝和吊兰各多少盆？

（2）规划组认为有比390 元更省钱的方案，请求出购买两种绿植总费用的最小值。

本题考查二元一次方程组的应用、一次函数的性质［3］。1.由绿萝和吊兰的关系可以列出二元一次方程组求解箱数；2.假设绿萝m盆，可以列出总费用W=3m+276，这是一次函数并且k＞0，可得W随着m的增大而增大，由题意绿萝盆数不少于吊兰盆数的2倍，所以且m为整数，确定自变量的取值范围，当m=31 时，总费用最小值为369 元。虽然考查的是一次函数的性质，但其实很多学生只是生搬硬套，在考试中只知道用计算的方法算出结果，却无法写出必要的文字说明，追根究底，是在一次函数的图象与性质学习过程中，不是数形结合，将图象与性质结合起来融会贯通，而是将两者分开，死记硬背结论。在日常教学过程中，应让学生充分感受题目中描述的情景，提取题目中的有效信息，把条件转化为符号语言和图形语言，给学生留下充足的时间进行深度思考，让学生感受用数形结合来描述事物变化的过程，从而提升学生的数学表达能力。

（二）对称性问题

案例2：（2019 年福建省中考数学试卷第10 题）若二次函数y＝|a|x2＋bx＋c的图象过不同的五点A（m，n），B（0，y1），C（3-m，n），D（2，y2），E（2，y3），求y1，y2，y3的大小关系（ ）

A.y1＜y2＜y3B.y1＜y3＜y2

C.y3＜y2＜y1D.y2＜y3＜y1

本题考查的是二次函数的对称性，在确定二次项系数是|a|＞0 的情况下，图象开口向上，再观察题目给出的五个点，A点和C点的函数值相同，由二次函数的对称性可得对称轴为，画出二次函数的图象，此时，离对称轴越近函数值越小，从而确定y1，y2，y3的大小关系。函数问题是初中数学学习的重难点，遇到函数问题，多采用数形结合思想。在函数教学过程中，需注重对函数图象与性质的探索与分析，让学生自己观察，试着总结，再得出结论，让学生充分感受到每一种函数图象的特点，如正比例函数、反比例函数、二次函数的对称性，使数量关系与几何直观巧妙结合在一起，让抽象的问题具体化，化难为易。

（三）求函数表达式问题

案例3：（2020 年福建省中考数学试卷第25 题（1）已知直线l1：y＝-2x＋10 交y轴于点A，交x轴于点B，二次函数的图象过A，B两点，交x轴于另一点C，BC＝4，且对于该二次函数图象上的任意两点P1（x1，y1），P2（x2，y2），当x1＞x2≥5 时，总有y1＞y2。求二次函数的表达式。

本题考查一次函数和二次函数的图象与性质。对于未知参数，常常需要结合函数图象，进行分类讨论。BC=4，C点坐标有两种情况，在B点的左边或者右边，C（9，0）或C（1，0），若抛物线过C（9，0），当5＜x＜7 时，y随x的增大而减小，不符合题意；若抛物线过C（1，0），当x＞3 时，必有y随x的增大而增大，符合题意。因此C（1，0）。利用B、C点坐标即可求出二次函数表达式。除了参数，函数中取值范围无法确定，取最大值或最小值等也需要数形结合进行分类讨论。忽视数形结合容易导致思维的局限性，考虑问题不全面，容易出现漏解、错解，数形结合则有利于提升学生的理性思维品质和分析综合能力，培养严谨的数学思维。

（四）几何问题

案例4：（2019 年福建省中考数学试卷第21 题）在Rt△ABC中，∠ABC＝90°，∠ACB＝30°。将△ABC绕点C顺时针旋转一个角度α得到△DEC，点A，B的分别对应点D，E。

（1）若点E恰好落在边AC上，如图①，求∠ADE的大小；

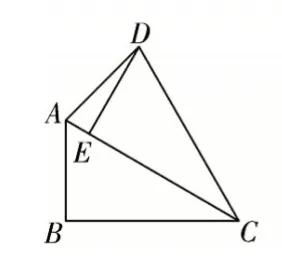
图①

（2）若α＝60°，F为AC的中点，如图②，

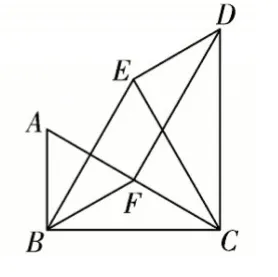
图②

求证：四边形BEDF是平行四边形。

本题考查图形的旋转、直角三角形、等腰三角形和平行四边形。（1）观察图形旋转前与旋转后的变与不变，将求∠ADE的大小转化为求∠CDA与∠CDE的差，利用旋转的性质和等腰三角形的性质得∠ADE=15°。（2）将求证四边形BEDF是平行四边形转化为求证DE与BF平行且相等，求证DE与BF平行，转化为求证一组内错角相等，利用∠DEC=90°，延长BF交EC于点G（如图③），得∠DEC=∠BGE=90°，问题（2）得证。几何是初中数学学习的重难点，学生遇到问题找不到切入点，在教学过程中需要引导学生通过观察图形，“将图形语言转化为符号语言，通过数形结合有利于将问题转化为已经掌握的知识，将复杂问题转化为几个简单的问题，将抽象问题转化为具体、直观的问题以便精确求解、化繁为简”［4］。

图③

四、启示与展望

数形结合思想的形成是一个长期的过程，需要在日常数学学习和教学过程中逐步渗透，形成系统化的数形结合思想认知结构。首先，教师在日常教学要有意识地渗透数形结合思想，培养学生从利用数形结合思想解决一道简单问题到用数形结合思想与其他数学思想方法共同解决一道复杂问题，逐渐增加难度。其次，教师需要引导学生在阅读题目中进行深度思考，提取题目中的有效信息，通过数形结合将题目中的条件转化为符号语言和图形语言；加强针对性，通过解决进阶式变式问题提升学生的逻辑性、综合性和探索性，训练学生的思维能力和探索能力，揭示数形结合的思想方法。最后，教师需要把最基本的知识点讲透，把利用数形结合思想解题的策略讲到位，在练习和纠错中不断巩固和深化，形成规律性的理性认识，培养学生灵活运用数形结合思想方法分析、解决问题的能力。

数形结合思想的形成不同于数学知识的理解、掌握和运用，它需要在知识教学与方法教学中形成，同时需要与学生的认知发展水平相适应［5］。数学结合思想是数学思想方法中的核心思想方法，是必修重视的数学核心素养，如何更好更有效渗透数形结合思想方法，让学生形成良好的数形结合认知视角和思维品质、提高学生的数学核心素养，仍然需要在教学过程中不断探索研究与完善。