信息技术支持下的小学数学问题链教学策略

杨传勇

（福州市湖滨小学，福建 福州 350025）

当我们面对数学问题时，进行内化、对比、综合、转化等一系列思维活动来解决这个问题后又产生新的问题或发现问题与问题间的联系。这种过程不断反复、深入，从而生成具有内在联系的若干问题，这形成了问题链。［1］而文中的数学问题链是指教师在现有数学课程标准的框架下，围绕一定的数学教学目标或某一核心问题，结合教学内容和学生已有的认知水平，设计出能激发学生新旧认知之间矛盾的、相对独立而又互相关联的问题组合。［2］现有小学数学问题链研究多从核心素养、高阶思维、深度学习等方面进行研究。这些研究从培养目标、问题设计、思考方式等角度为小学数学问题链提供了丰富的理论基础，但缺乏可供一线教师实践的具体方法和策略。现在信息技术高速发展，专用教学设备、教学软件迭代频繁。凭借这些先进的信息技术手段，教师可以更好地发挥小学数学问题链教学的优势，促进学生数学思维的生成。而笔者查看了现有的各类教育教学文献，已有的研究撰写时间久远，多媒体设备大多已经过时，不具有指导、借鉴意义。

对小学数学而言，一个好的问题不仅仅是触发学生数学思考的契机，同时能激发学生的学习兴趣、求知欲。而一串高效的数学问题链则可以让学生保持着一种主动、积极的态度去开展学习，同时在潜移默化中学会提出问题的策略和解决问题的思路，将教师的问题链转化成学生自己的学法链，最终形成有个人特色的数学思维逻辑链。［3］尤其在新课改的环境背景下，教师在课堂教学中用一连串高效的问题将学生的学习思维过程串联，在问题链的引导下，学生通过思考、探究、操作等一系列的活动获得数学知识正是体现了学生数学学习的主体地位。

数学知识是抽象的，而信息技术能将数学知识表征形式多样化、可视化，搭建学生由具体形象思维向抽象逻辑思维转化的技术平台。数学问题链是小学数学课堂教学中一种高效的教学组织形式；而信息技术教学是教学手段，它为问题链教提供技术支持。二者有机结合，不仅可以做到快速收集学生数据，反馈结果及时、准确，还能利用网络打破时间、空间的限制，让学生的思考更加深入。

一、课前调查学生学情，助力问题链的生成

教师创设问题链，是建立在对学生已有的认知水平正确认识的基础上，再根据数学课程教学目标，设计出一套能够激发学生新旧知识之间矛盾的问题组。在此，教师对学生学情的了解至关重要。问题链深度不够，学生不假思索就能得到答案，这样学生得不到锻炼，思维方式就停滞不前；问题链难度太高，学生无法通过自身已有认知得到答案，体会不到解决难题后的愉悦，长此以往学生容易产生厌学情绪。以往，教师对学生学情的了解都来源于学生课堂表现、作业完成情况和考察评价这三个方面。但这些方面受到各种因素的影响和条件的制约，教师的感受是片面的、主观的、模糊的。在信息技术的加持下，教师可以在课前利用微信小程序《问卷星》或钉钉里的智能填表等程序对学生进行摸底或调查，获得对学生学情的精准了解，让设计的问题链有的放矢，更加贴近学生思维水平。

首先，可以在课前针对学生在学习中所要用的知识掌握情况，进行调查。例如《圆的面积》这一课，它的问题链中关键的一环是在回顾已学平面图形的面积公式推导过程，总结发现转化（化归）思想。但常有部分学生只死记硬背面积公式，遗忘面积公式的推导过程，这样他们在课堂就失去了辨析、归纳、总结转化思想的能力。但如果教师在课前进行问卷调查：“我们学过哪些平面图形？”“它们的面积是在哪里”“它们的面积公式是什么？”“它们的面积公式是怎么推导出来的？”在这样一连串的问题提示下，学生不仅将已有相关知识温习了一遍，而且在潜意识中建构起已有知识的脉络。

其次，可以对学生在日常生活中掌握的数学信息程度进行了解。数学知识来源于生活，有些知识学生在上课前就已经掌握。如《小数的初步认识》中小数的读写法，教师可以在课前通过问卷调查了解学生掌握情况，如果大部分学生会念会写，教师在问题链设计时就对这知识点到为止，课堂不挤占太多时间进行追问思考。课前调查表还能精确定位到某个学生相关知识不足，教师再利用课余时间对他进行针对性的相关训练。

最后，学生情感价值、学习态度等也都是可以进行调查，然后再经程序统计反馈给教师的。问题链是冰冷的逻辑链。课堂上教师如果只注重挖掘新授知识的思维逻辑的话，就容易让学生产生疲惫感，不易保持集中思考的状态。但如果在教学那些比较枯燥的数学知识之前能够进行课前调查，如调查反馈出大部分学生感兴趣生活场景，教师就能在课堂导入部分创设与课堂知识相关的相似生活情境，以便学生更快地投入学习，用积极地学习态度思考问题。

二、课中借助信息技术，问题链全过程呈现

数学相关知识之间是有脉络的，教师用一连串的问题链将新旧知识之间的联系和区别连接起来，搭建起学生学习的知识链。教师通过问题链的呈现—聚焦—反馈—对比—形成结论这样反复的过程帮助学生思考，催化学生的学习链的生成。最终学生通过长期训练就能形成解决问题的数学逻辑思维链。这个过程在以往只能通过教师在课堂上长年累月的教学，学生慢慢形成。而现在可以利用信息技术将问题链解决过程中各个环节内容可视化，加速学生逻辑思维链的形成。

（一）根据知识特点，呈现逻辑链可视化

一节课有许多的问题，这些问题之间有些是有逻辑关系的。一个问题的解决又催化了另一个问题的生成。如果只用板书，是很难在课堂上呈现出这种逻辑性的。借助信息技术，教师可以根据教学内容的特点和逻辑性，选择生成不同的问题链呈现形式，如树状图、流程图、圆圈图等。如解决问题、计算教学这些课型问题链呈现形式是流程图，概念教学问题链呈现形式是树状图。问题链随着课堂进度呈现在屏幕上，帮助学生理解并掌握知识的发生、发展过程或熟练技能的操作流程。

以《用字母表示数》为例，教师一上课时就直接揭示课题，然后问学生：“你看到这个课题，你想了解什么？”学生通常会回答：为什么用字母表示数？字母表示数的意义是什么？字母可以表示哪些数？等等。教师在这里可以利用“希沃白板5”的思维导图功能将这些问题按照逻辑顺序有选择地呈现在白板上（如打字慢的教师可以在课前将问题预设好，再利用添加遮罩功能将问题隐藏）。之后即便在课堂突发事件中的生成性问题也能很好地添加至问题链。这节课的问题链就完整地呈现在学生面前，便于学生梳理思路。在上课过程中，这个问题链就一直显示在屏幕上，成为学生课堂学习的提纲。［4］（见图1）

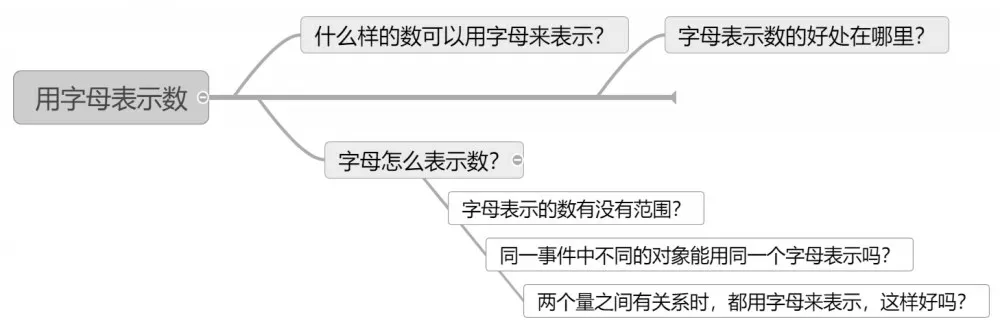
图1 《用字母表示数》课堂问题链

（二）助力问题解决，知识呈现直观化

数学问题链中，一个问题扣着一个问题，衔接紧密，如同链条一般。一个问题无法解决势必无法引出下一个问题。因此，问题的解决就显得尤其的重要。信息技术最大的作用是将数学知识表征可视化，将那些枯燥、抽象的数学知识直观呈现出来，动态展示变化过程，帮助学生理解、分析、判断。

如教学《圆的面积》时，圆与长方形之间的关系一直都是重难点。尤其是圆通过分割，移动拼成一个近似的长方形这个过程中让学生感受极限思想。在这里，学生通过动手操作，观察等一系列的学习活动，感知随着圆平均分份数的增加，近似长方形的长在逐渐变直。但在实际操作中，学生的操作是有局限性的，最多只到16 等分，学生无法感知极限思想，不容易将圆和长方形联系起来。但利用几何画板等软件，教师可以接着学生的操作，在电脑中将圆32 等分、64 等分……借助圆转化成长方形的直观演示向学生渗透极限思想。同时为下一个问题圆的面积公式如何推导打下良好基础。

（三）大数据收集，让思考结果数据化

信息技术不仅将问题链直观地展示在学生面前，让学生依照这问题链逐渐形成类似课型的学习链、思维链，同时能将学生掌握情况进行实时数据统计，再以图表形式反馈出来，便于教师发挥主导作用，引领学生进行思辨。同时让学生感受数学统计学的美。

例如，《用字母表示数》这节课的难点也是重点：两个量之间有关系时，这两个量都用字母表示好吗？有的认为可以用两个不同的字母表示，有的认为用字母式表示等。这时教师不急于公布答案，可以将这些意见列举出来，然后让学生利用答题器进行投票。电脑收集学生的答案后，立即将数据进行统计，瞬时生成关于学生投票统计表，直观地展示在学生面前。教师通过统计表查看学生投票情况，让学生进行分组讨论。学生通过思辨，再次利用答题器对该问题进行投票，询问学生为什么更改答案。在两次的选择中，学生通过思考、对比、讨论、倾听，就会统一思想，寻找到最优答案。

（四）因人而异，让思考深度个性化

有条件的学校，班级学生都配备了平板。在上《综合与实践》这一类型的课时，教师还可以根据学生不同的认知水平在课堂上推送详略不同的问题链或不同难度的练习到学生平板，帮助学生思考。这样真正实现“人人都能获得良好的数学教育，不同的人在数学上得到不同发展”的数学课程理念。

三、课后记录问题链，将问题链延伸、完善

一堂课的结束并不意味着学生对这一相关数学知识的思考就结束了。学生还能在信息技术的帮助下，收集资料继续思考、学习。课后学生可以借助XMind 思维导图、微软的OneNote、Notability 等软件将课堂上的问题链收集下来，便于后期修改、完善。

学习有困难的学生可以将每天课堂的问题链利用笔记软件快速记录下来。他们只要利用课余时间沿着问题链的顺序一个一个弄清问题答案，也就逐步掌握了知识的生成过程和运用方法。尤其是Notability 这类软件强大的录音功能，能做到与笔记同步。找到记录问题的笔记，就能同步听到这个问题前后的课堂录音，非常适合对课堂知识有困惑的，课后需要反复回放录音加深理解的学生。

学有余力的学生可以将每天的课堂问题链收集起来，整合到同一单元知识或同一知识体系结构图中。在收集、整合过程中，传统的记录本因尺寸限制、修改不易等弊病耗时耗力，不如XMind 思维导图、微软的OneNote 等专业软件方便。当单元学习结束后，这个单元问题链就是这个单元的知识结构图。当学期结束时，学生再将单元链整合到如统计、图形、代数等各大类的知识中，形成整个知识网络图。学生通过收集、整合问题链的过程，对整个知识脉络起到了复习的作用。班级学习小组之间还能通过网络资料共享，互相合作，共同编辑课堂笔记和完善知识结构图、共同进步。

对数学有兴趣，思考能力强的学生可以在一个单元结束后，继续思考，将知识网络图自行往深处延伸。就像欧式几何利用五条公理将所有几何命题连结成逻辑网络一样去拓展自己数学知识的广度，延伸数学知识的深度。小学数学教材螺旋上升的编排方式，让部分学生对一个单元内容的学习意犹未尽，总想接着学习相关知识。如部分学生四年级上学期学习了复式条形统计图，当下学期学完单式折线统计图时，他们就能根据以往问题链的思考方式，自问自答，自己拓展出复式折线统计图。