特大输电塔地脚螺栓基础安全评价与优化设计
2022-09-19宁帅朋李布辉张庆张立裴方程王金昌
宁帅朋, 李布辉, 张庆, 张立, 裴方程, 王金昌*
(1.中国能源建设集团江苏电力设计院有限公司, 江苏 南京 211102;2.沈阳建筑大学 交通工程学院, 辽宁 沈阳 110168;3.浙江大学 建筑工程学院, 浙江 杭州 310058)
0 引言
随着我国经济建设的高速发展,各个行业对电力供应的需求迅速增加,而电网承担着保证发电与供电安全可靠的作用。输电塔作为电网重要的组成部分,有时需要跨越江河等,对特大型输电塔的设计建造提出了新的考验。
部分学者针对地脚螺栓连接形式的输电塔基础展开研究:张凯旋等[1]针对不同锚固长度的光圆型、锚板型地脚螺栓展开抗拔试验,结果表明在荷载作用下地脚螺栓有3种破坏形式。针对地脚螺栓刚性塔座板承载力进行了试验研究,并系统提出了全新的建议计算公式[2-5]。刘俊卿等[6-7]针对架空输电线路铁塔的地脚螺栓塔脚板进行了抗拉承载力试验研究,结果表明底板厚度和加劲板的作用对塔脚板承载力影响较大。藏祥生等[8]针对四组合锚板型地脚螺栓进行了抗拔承载力试验,结果表明,与单个地脚螺栓相比可显著提高极限抗拔承载力,且随着锚固深度加大,抗拔承载力由混凝土开裂强度控制变为螺栓的抗拉强度控制。Trautwein等[9]针对地脚螺栓的抗拔承载力进行试验研究,总结抗拔荷载与竖向位移之间的关系。Ožbolt等[10]开展了地脚螺栓直径对混凝土破坏模式和位移影响的试验研究。综上所述,已有地脚螺栓的研究大多基于试验展开对单根锚杆的抗拔特性和破坏模式展开,但鲜有针对整体式锚板锚固下的特大型输电塔地脚螺栓连接基础的研究。
本文依托某特大跨江输电塔工程的设计实践,利用Diana有限元分析软件对输电塔基础进行数值模拟,得出整体式锚板锚固的地脚螺栓连接形式下的基础应力分布和混凝土裂缝宽度及发展规律,优化锚板的布置形式,本文的研究结果对类似特大型输电塔基础地脚螺栓的连接提供参考。
1 工程背景
1.1 特大跨越输电塔概况
某输电项目线路全长175.6 km,其中常规线路171.6 km,大跨越段4.06 km。大跨越段拟采用“锚塔-跨越塔-跨越塔-锚塔”的跨越方式过江,耐张段全长4 060 m,跨越档距2 560 m,档距分布为750、2 560、750 m,跨越塔呼高为347.5 m,全高为390 m。
其中跨越塔采用钢管混凝土塔,最大主材截面直径为2 100 mm,钢管材质为Q420 C,内部填充强度等级为C50的自密实混凝土。主管采用内外法兰连接,主管与支管采用相贯节点。横担与塔身连接节点、变坡处节点采用铸钢节点。由于跨越塔高度、自重较大,因此对特大型输电塔基础承载能力提出了较高的要求。杆塔与基础连接位置处于复杂的拉剪耦合状态,基础采用整体式锚板锚固的双排地脚螺栓连接形式及其相应的配筋方案,针对该特大型跨越式输电塔工程的基础设计方案进行分析验证。
输电塔基础平面布置图如图1所示,基础采用承台灌注桩方案,4个基础为独立式基础,承台之间采用混凝土连梁。桩基础采用5×6的布置方案,桩长56~65 m,承台旋转45°,承台尺寸15.4 m×18.7 m,厚度2.5 m,承台上方柱体高度为2.5 m,基础总高度为5 m,基础之间距离A=B=75 m,连梁宽1.6 m,深度为2 m。

图1 基础平面布置图
柱体配筋方案如图2所示,基础设计方案如图3所示。

图2 基础配筋方案

图3 基础设计方案
1.2 荷载工况
荷载分为自重荷载和外荷载。自重荷载可以根据各个构件的材料密度在Diana有限元分析软件中自动添加,而外荷载需要通过计算分析确定。
由于上部结构为钢管混凝土结构,上部结构分析按纯钢管、钢管混凝土抗拉刚度相同和钢管混凝土抗拉刚度不同3种方案计算,基础计算取包络值(加粗值)。根据目前杆塔计算结果,基础受拉作用力见表1。

表1 基础受拉作用力
1.3 整体式锚板锚固的地脚螺栓设计方案
该方案采用8.8级地脚螺栓,螺栓总长度为3 700 mm,锚入深度为3 400 mm,材质为42CrMo,双排布置40M80。锚板厚度为40 mm,内径为1 300 mm,外径为2 800 mm,材质为Q355B钢,采用螺栓连接的形式固定在地脚螺栓末端。地脚螺栓连接平面布置如图4所示。

图4 地脚螺栓布置方案
2 材料本构模型
2.1 混凝土开裂塑性模型
混凝土采用总应变裂缝模型,该模型由Litton等[11]提出,其开裂后的关系主要通过拉伸行为、剪切行为和受压行为来共同确定。此外Diana软件提供丰富的混凝土拉伸软化模型曲线和压缩模型曲线用于混凝土开裂下的非线性运算,同总应变裂缝模型相比,由文献[12]提出的多向固定裂缝模型无法模拟受压状态。总应变裂缝模型依据裂缝方向与主应力方向始终保持一致的原则,选择正交旋转的方式,该模式下裂缝的方向随着主拉应力的方向不断变化,不仅可以更加精确地对构件进行模拟,而且不需要设置剪力传递机制,其剪切模量可以自动通过弹性模量和泊松比计算得到。
① 混凝土拉伸软化应力-应变曲线采用指数模型曲线[13],如图5所示。指数模型是常用的拉伸软化模型,这种模型在达到极限拉应力前的下降段为非线性曲线,可以更好地适用于非线性分析计算,同时在材料的本构模型中考虑了结构的断裂能和裂缝带宽。

图5 指数函数拉伸软化模型曲线
按下列公式确定Exponential拉伸软化应力应变曲线关系:
(1)
(2)
(3)
fcm=fck+Δf,
(4)
式中:ft为混凝土极限抗拉强度;GF为混凝土断裂能;fcm为混凝土平均抗压强度;εu为混凝土极限应变参数;fck为混凝土轴心抗压强度标准值;Δf为混凝土平均抗压强度修改参数,按推荐值取8 MPa;heq为裂缝带宽,由初始裂缝方向和单元尺寸决定,该物理量的计算由有限元软件自动完成。
② 混凝土受压应力应变曲线采用常用的抛物线形受压模型曲线,如图6所示。

图6 抛物线受压模型曲线
按下列公式确定抛物线受压软化应力应变曲线:
(5)
(6)
(7)
(8)
(9)
Gc=250GF,
(10)
(11)

本文根据设计方案,采用强度等级为C35混凝土。依据规范[14],fck=23.4 MPa,ftk=2.2 MPa,E=3.15×104MPa,μ=0.2。根据式(3)、(4)、(10)可以得出C35混凝土拉伸软化和受压软化曲线的关键参数:断裂能GF=0.1358 N/mm,受压断裂能为Gc=33.94 N/mm。
2.2 钢材理想弹塑性本构模型
钢材采用理想弹塑性模型,不考虑应变硬化导致的应力增加和屈服强度上限。钢筋以“Grid”钢筋网片单元形式嵌入进混凝土实体单元之中,与混凝土形成一体共同变形,从而为母体单元贡献刚度,该单元类型适合箍筋或一个面上等间距分布的纵筋情况。各种钢材的设计参数见表2。

表2 材料参数
2.3 接触界面本构模型
2.3.1 地脚螺栓与混凝土接触面
大跨越输电塔基础尺寸与螺栓尺寸相差悬殊,对地脚螺栓进行简化处理,可将地脚螺栓简化为嵌入式梁,其与混凝土的界面则被简化为2个法向与1个切向刚度的界面单元。
为了验证数值结果的可靠性,与地脚螺栓抗拔承载力性能试验进行对比,如图7所示,试验构件分为地脚螺栓锚固的立柱部分以及圆形固定端2个部分,通过8 根连接螺栓下反力钢梁连接;试验中上拔力采用液压千斤顶自动加载、稳载与恒载。通过RS-JYB/C 型静载荷测试分析系统全自动实时观测与记录。其中浇筑混凝土强度等级为C25,基座为高度为0.9 m、半径为0.9 m的圆柱形,混凝土柱截面为0.6 m×0.6 m的正方形,高度为1.8 m。地脚螺栓直径为60 mm,其中地脚螺栓的锚固深度为1.5 m,布置于立柱中心。数值模型依照实际试验建模,分别设置底端无锚固和带锚固2个工况,并对此展开非线性数值分析。

图7 地脚螺栓试验装置
通过参数分析可知螺栓与混凝土截面法向刚度对计算结果基本无影响,因此在计算中2个方向的法向刚度均设为较大值1×1012N/m3,根据试验数据拟合得出地脚螺栓与混凝土柱体的黏结强度为
(12)


图8 数值计算与试验结果对比
2.3.2 锚板与混凝土接触面
考虑锚板表面光滑,与混凝土的粘结力较小,因此设定锚板与混凝土之间不受拉。两者受压接触界面单元需要设置法向刚度和切向刚度,根据Diana用户手册[15]中推荐的方法设置合理值:
① 考虑网格模型中的单元平均尺寸,如果网格模型中单元尺寸变化幅度大,则取界面单元附近的单元平均尺寸,设为Ie。
② 假定弹性模量E,其数值介于界面两侧材料的弹性模量。
③ 法向刚度值可以表示为Kn=E/Ie,切向刚度值可以表示为Kt=Kn/10
3 基于裂缝机理的输电塔基础安全性评价
3.1 输电塔基础数值模型
模型网格划分如图9所示。地脚螺栓简化为嵌入梁,塔脚板和锚板采用壳单元,地脚螺栓与塔脚板和锚板固接,钢筋网片嵌入进混凝土中。基础底部的桩基础被忽略,底部施加三向完全约束。建模时忽略输电塔的上部结构,为了避免上部荷载直接施加在塔脚板上导致塔脚板局部应力过大,在塔脚板上建高度为2 m的塔脚模型,将1.2节计算的上部荷载作用在塔脚上,并对由此产生的多余弯矩进行补偿。

图9 输电塔基础数值模型
3.2 计算结果
如图10所示,在标准设计上拔荷载下,地脚螺栓最大Von Mises应力为378.56 MPa,未达到螺栓屈服强度,螺栓最大轴力1 660 kN。地脚螺栓顶部应力最大,不同螺栓间的轴力水平不同。

(a)应力
如图11所示,在标准设计上拔荷载下,地脚螺栓最大竖向位移为6.14 mm,基础混凝土部分的最大竖向位移为1.81 mm,发生在与锚板上表面接触的区域,混凝土与地脚螺栓之间存在相对位移。

(a)地脚螺栓
荷载因子为0.5时,如图12(a)所示,混凝土最大裂缝宽度为0.26 mm,出现在锚板与螺栓连接部位,此时螺栓顶部裂缝很小,小于0.15 mm。当荷载因子为1.0时,如图12(c)所示,即在标准上拔荷载下,裂缝主要以0.15 mm以下的微裂缝为主,混凝土最大裂缝宽度为1.00 mm,位于锚板附近,属于深层裂缝且未发展到混凝土表面,不影响基础的耐久性,螺栓顶部裂缝宽度小于0.87 mm,考虑剪力槽厚度为40 cm的细石混凝土保护层,可以有效阻止空气和水对钢筋的侵蚀,因此不影响基础的耐久性。荷载因子为1.5即标准荷载的1.5倍时,如图12(c)所示,最大裂缝宽度达到3.14 mm,集中在锚板底部。
结合图12(b)、(d)和(f)的各个荷载因子下的裂缝分布剖面图可知,随着荷载的增大,锚板附近裂缝从锚板边缘由内而外发展,呈现倒锥形,基础顶部混凝土裂缝从外圈螺栓顶部逐渐向混凝土深部和内圈螺栓发展。
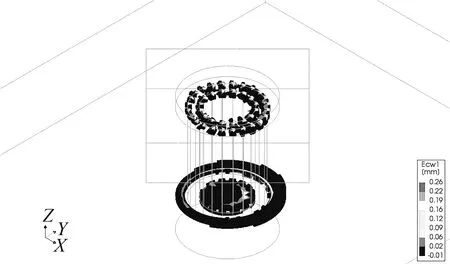
(a)荷载因子0.5
3.3 裂缝机理分析
本文依托特大型跨越式输电塔工程,针对采用整体式锚板锚固的地脚螺栓连接形式的基础,利用Diana有限元软件模拟基础在实际工况下裂缝的发生、发展和演化,探究基础裂缝发展的规律,进一步揭示该连接形式下裂缝机理。
① 上拔工况下基础内存在裂缝,从裂缝分布区域、深度及大小来看,并不对基础的安全产生威胁。绝大部分裂缝属于微裂缝,钢筋网可以有效约束其扩展范围,部分裂缝宽度较大但是位于基础深处或者拥有较厚的保护层,不影响基础耐久性。
② 上拔工况下,裂缝主要集中在螺栓顶部和锚板附近。由于水平分力的存在,各个地脚螺栓的内力并不相同。荷载沿地脚螺栓分布不均,但是锚板的存在相当于增大地脚螺栓底部的刚度,同时整体式锚板会使上方混凝土产生一定的竖向位移,减小螺栓与混凝土的粘结滑移作用,因此削弱了不均匀性。螺栓孔顶部承受荷载最大,且与混凝土滑移最大,因此地脚螺栓顶部产生裂缝并由此向下延伸。锚板上部与底部混凝土裂缝均较大但裂缝的性质不同,上拔力传递至整体式锚板上,使得锚板上方混凝土形成了压应力区,裂缝以倒锥形向混凝土表层扩散,属于纵向裂缝。锚板底部混凝土受拉产生裂缝,属于横向裂缝。
4 基于承载力和裂缝发展的输电塔基础优化设计
整体式锚板的锚固作用可以有效提高极限抗拔承载力和抗裂性能,本文在原设计方案的基础上,按照位移加载的方式对锚板进行参数分析,进一步优化锚板的布置。
4.1 锚板厚度的优化设计
为了研究锚板厚度对基础承载力的影响,将锚板厚度分别设置为20、30、40、50、60、80、100、120 mm,通过位移加载的形式,计算分析得出基础的荷载位移曲线,如图13所示。
由图13可知,随着锚板厚度的增加,基础的破坏模式发生变化。当锚板厚度为20 mm和30 m时,螺栓从混凝土中抽出,特点为达到极限承载力之后荷载位移曲线存在一段平台期。当锚板厚度增大到40 mm及以上时,基础发生螺杆拉断破坏,特点为达到极限承载力之后承载力迅速下降,根据应力云图显示此时地脚螺栓达到屈服应力。

图13 不同锚板厚度下柱脚顶端荷载位移曲线
锚板厚度可以显著提高基础抗拔能力。当荷载较小时,各个模型的荷载位移曲线基本重合,说明基础承载力受锚板厚度影响较小,锚板厚度只对后期荷载较大时有影响。原设计方案的锚板厚度为40 mm,当锚板厚度从40 mm增加到50、60、80、100、120 mm,基础承载力分别提高了11.2%、17.3%、26.9%、24.7%和32.8%,承载力的增长趋势总体上逐渐减小。考虑经济性,锚板厚度不宜过大,因此最佳锚板厚度为80 mm,即1.0倍的地脚螺栓直径。
为了比较锚板厚度对抗裂性能的影响,分别提取荷载为40 000、60 000、80 000 kN时不同锚板厚度下基础最大裂缝宽度,如图14所示。

图14 不同上拔荷载下最大裂缝宽度随锚板厚度变化曲线
由图14可知:上拔荷载为40 000 kN时,基础最大裂缝宽度随锚板厚度增加逐渐减小然后趋于稳定,宽度从0.66 mm减小到0.4 mm左右,减小了39.4%;上拔荷载为60 000 kN时,基础最大裂缝宽度随锚板厚度增加几乎不发生变化,维持在1.0 mm附近;上拔荷载为80 000 kN时,基础最大裂缝宽度随锚板厚度增加先减小后增大,锚板厚度为80 mm时裂缝宽度最小为3.12 mm,相比原方案锚板厚度40 mm下3.52 mm的裂缝宽度缩小了11.4%。
综合极限承载力和抗裂性能来看,锚板厚度取80 mm,即1.0倍的锚栓直径。
4.2 锚固深度的优化设计
为了研究锚固深度对基础承载力的影响,D为锚板的外径2 800 mm,设置不同的锚固深度分别为0.8D、0.9D、1.0D、1.1D、1.2D、1.3D和1.4D,通过位移加载的形式,计算分析得出荷载位移曲线,如图15所示。
由图15可知,随着锚固深度的增加,基础承载力和刚度均在逐渐增加。锚固深度为0.9D、1.0D、1.1D、1.2D、1.3D和1.4D的极限承载力与0.8D相比分别提高了6.3%、10.3%、12.8%、14.5%、17.9%和21.2%,可以看出增长趋势逐渐缩小,当锚固深度达到原方案(1.2D)后,增长趋势重新变大。锚固深度为原方案(1.2D)、1.3D和1.4D的基础承载力均处于较高水平。为了比较锚板厚度对抗裂性能的影响,分别提取荷载为40 000、60 000、80 000 kN时不同锚固深度下基础最大裂缝宽度,如图16所示。

图15 不同锚固深度下基础荷载位移曲线

图16 不同上拔荷载下最大裂缝宽度随锚固深度变化曲线
比较各自的曲线,结果表明,锚固深度的增加可以有效减小基础最大裂缝宽度。上拔荷载为40 000、60 000 kN时,基础最大裂缝宽度随锚固深度增加而减小,当锚固深度达到1.3D之后,裂缝宽度的变化趋于稳定,分别为0.2、0.5 mm左右,相比原方案(裂缝宽度分别为0.37 mm和1.2 mm)各自减小了46.0%和58.3%。当上拔荷载为80 000 kN时,基础最大裂缝宽度随锚固深度增加波动变化,总体上大幅度减小。
综合极限抗拔承载力和抗裂性能来看,锚固深度取1.3倍的锚板外径。
5 结论
以某特大跨江输电塔工程为研究背景,基于整体式锚板锚固的地脚螺栓连接设计方案,对方案的安全性进行评估,探究该连接形式下裂缝的产生和发展机理。同时,为了提高基础的极限承载力与抗裂性能,在原有设计方案的基础上,对锚板的布置形式进行优化与研究。主要的结论如下:
① 通过与试验结果的对比,验证了简化地脚螺栓数值模型的有效性。简化嵌入梁与混凝土界面刚度是控制螺栓拉拔特性的重要参数,本文基于数值计算给出了三向刚度的建议取值。
② 对设计方案进行了安全性评价,上拔工况下,基础承载力满足要求,混凝土可以正常带裂工作。
③ 锚板厚度的增加可以有效提高基础的极限抗拔承载力,同时延缓裂缝的产生和发展。根据参数分析结果,锚板厚度取1.0倍的锚栓直径。
④ 锚固深度的增加可以提高基础的极限抗拔承载力,在荷载较小时,可以有效延缓裂缝的产生和发展。根据参数分析结果,锚固深度设置为1.3倍的锚板外径。
