旋转阻尼器系统计算模型与参数匹配分析

2022-09-19黄本韬杜群贵

机床与液压 2022年5期

关键词：转轴推杆凸轮

黄本韬，杜群贵

(华南理工大学机械与汽车工程学院，广东广州 510640)

0 前言

在家电、办公设备、家居、汽车工业等行业中，一种使盖板结构下降速度可控的旋转阻尼器被广泛使用，其结构如图1所示。

图1 旋转阻尼器内部结构

该类型阻尼器的关键结构由圆柱凸轮机构(由元件1、2组成)、弹簧3、黏滞阻尼器4组成。转轴与盖板旋转中心相连；转轴与推杆间通过螺旋面相接触，构成凸轮传动结构。在盖板下落时，转轴旋转使得推杆位移压缩弹簧与黏滞阻尼器，弹簧与黏滞阻尼器产生的阻力会通过凸轮转化为阻力矩输出，使盖板的下落速度得到控制。该阻尼器中，通过圆柱凸轮结构实现角位移与直线位移、力与力矩的转化；弹簧结构起到储存盖板能量与复位的作用；黏滞阻尼器起到耗散能量、控制下落速度的作用。

目前，尚未有对该类型旋转阻尼器系统的相关研究。为对该阻尼器系统的设计提供理论依据，对凸轮机构的传动作用与弹簧和黏滞阻尼器的输出特性分别进行分析，建立阻尼器的理论计算模型；对系统的参数匹配进行分析，并通过实验验证理论计算模型的正确性。

1 理论计算模型的建立

1.1 凸轮传动分析

圆柱凸轮传动结构由转轴与推杆组成，转轴与推杆的接触面为螺旋面，其结构与旋转行程如图2所示。

为转轴旋转时对应的盖板下落角度，=0°对应盖板垂直于地面的位置，=90°对应盖板下落至底部的位置。盖板在下落角度达到后，转轴和推杆的螺旋面相互接触，推杆被推动并位移压缩弹簧和黏滞阻尼器。旋转阻尼器的主要工作行程为螺旋面接触的部分，其余行程输出力矩很小，在计算中可忽略。

转轴与推杆上的接触面为螺旋面且参数相同，取转轴的螺旋面进行螺旋面参数位置的标注，如图3所示。

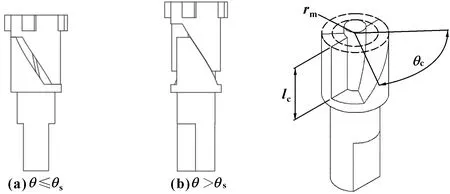
图2 圆柱凸轮结构与旋转行程图3 螺旋面结构参数

其中：、和分别为螺旋面的高度、角度与中径。对于下落角度为、角速度为时推杆的位移与速度，结合螺旋面的传动特征与圆柱凸轮的旋转行程，有：

(1)

对上式进行微分可得：

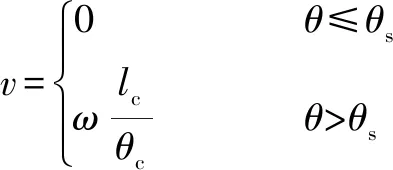
(2)

设凸轮传动结构在推杆压缩弹簧与阻尼器方向的行程为正行程，复位时为反行程，将转轴与推杆间滑动螺旋副之间的作用力集中在中径，将它展开为直角三角形，并将推杆与外壳之间的作用力集中到一个移动副，对正行程时的凸轮传动结构作力学分析，如图4所示。

图4 凸轮传动机构受力分析

其中：为推杆与转轴之间的相互作用力；为旋转阻尼器输出的阻力矩在半径为处转化得到的力；为该凸轮螺旋面对应的升角；为弹簧与黏滞阻尼器输出的阻力；、分别为外壳对转轴、外壳对推杆的作用力；、和分别为外壳与转轴、转轴与推杆、推杆与外壳之间的摩擦角，其对应的摩擦因数分别为、和。

对于凸轮螺旋面升角，有：

=arctan [/()]

(3)

由力矩的定义，有：

(4)

由几何原理得力矩与力的关系：

(5)

=(/)

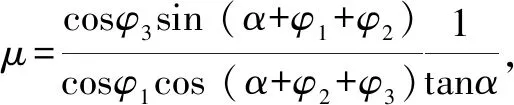
(6)

凸轮传动结构应满足在正行程可自行下落，在反行程可自行复位，在两个行程都不应发生自锁现象。在正行程时，主动构件为转轴；反行程时，主动构件为推杆。对两个行程进行分析，如图5所示。

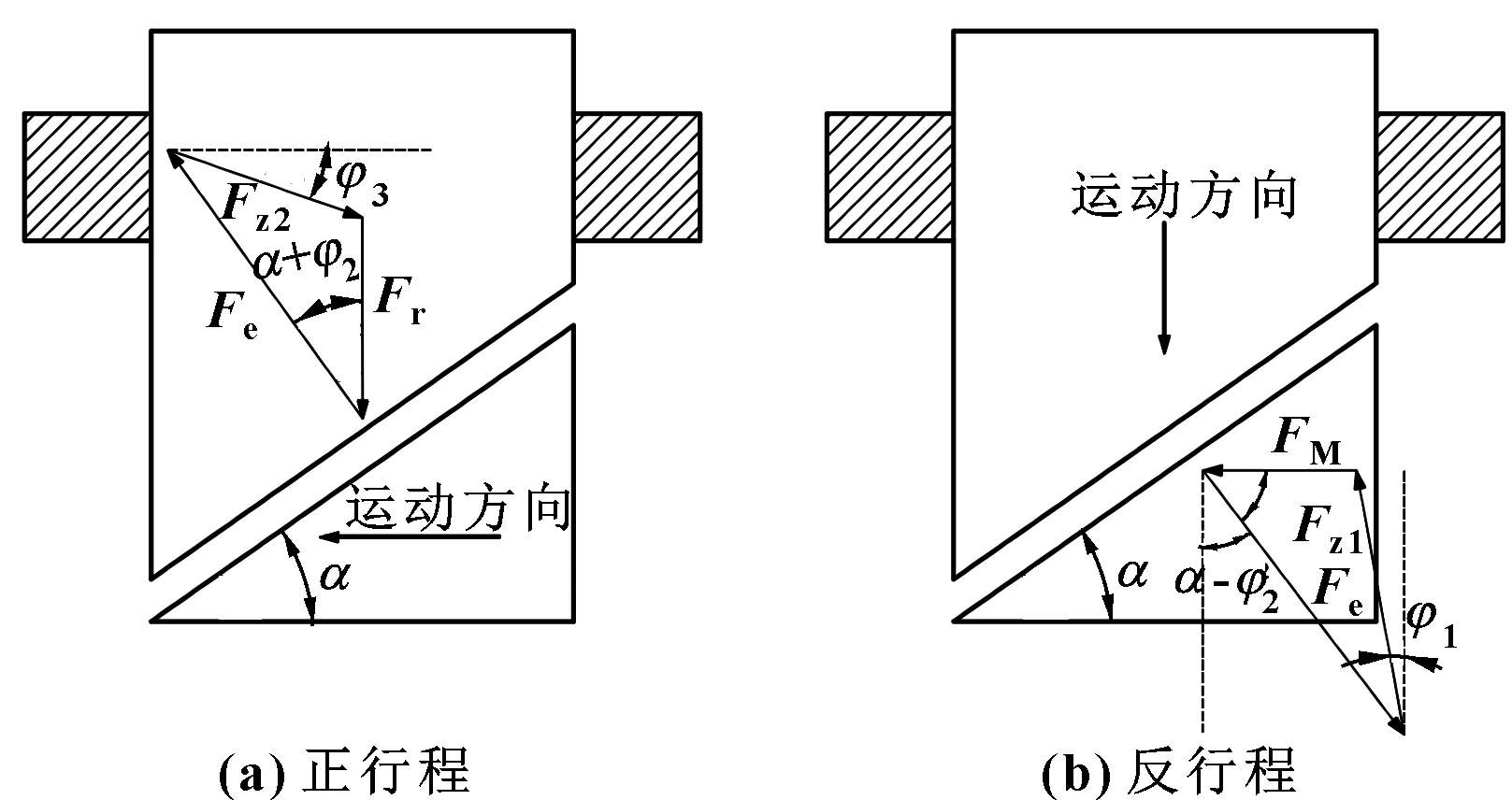
图5 凸轮传动自锁分析

由自锁原理，两个行程不发生自锁的条件为

(7)

1.2 弹簧与黏滞阻尼器输出分析

弹簧阻尼器系统输出的阻力由弹簧输出的力与黏滞阻尼器输出的力组成：

(8)

设弹簧的刚度为，在被压缩前存在预紧长度，其输出的力为

=(+)

(9)

弹簧输出的阻力与转轴的角位移相关，结合式(1)(6)(9)，弹簧输出的阻力矩为

(10)

弹簧是位移相关的阻力元件，因此在下落过程中弹簧输出的力矩应小于盖板的重力力矩，以确保盖板可自行下落。对不同下落角度下盖板重力力矩与弹簧输出力矩作图并进行分析，结果如图6所示。

图6 弹簧输出力矩与重力力矩对比

结合图6和式(10)分析可得，弹簧的刚度与预紧长度应满足以下不等式：

(11)

黏滞阻尼器为油缸型阻尼器，其内部结构如图7所示。

流域和各省的水功能区划已经批复多年，随着经济社会发展和对水功能区的认知水平提升，当年划定的水功能区划已有部分成果与现实需求不相适应，如部分保留区长度过长，且区内有集中城镇存在；部分饮用水源区无取水要求或在取水口下游划分长度过长等。但在《水功能区监督管理办法》出台前无水功能区调整程序规定，无法操作。虽然2017年出台的《水功能区监督管理办法》规定了调整程序，但对水功能区调整的技术要求和审查要求并未配套出台，现阶段仍难以操作。

图7 黏滞阻尼器内部结构

活塞在油缸缸体内活动时，内部的阻尼液体介质通过活塞两侧的阻尼间隙流动。由于流体具有较高的黏度而阻尼间隙较小，体积减小一侧的腔室会形成较大的压力，在活塞两侧造成压力差，输出阻尼力。

黏滞阻尼力的输出性能模型使用非线性输出模型：

(12)

式中：为阻尼系数；为速度指数，范围为0.3～1.95。二者取决于油缸、活塞的结构参数与阻尼液体介质。

1.3 系统性能求解

对于如图8中质量为、质心距旋转中心为的盖板的旋转阻尼器系统，在盖板下落时，在重力的作用下，盖板系统受到沿盖板下落方向的重力力矩，在盖板下落角度达到90°时，该力矩达到最大值=。与此同时，在旋转阻尼器的作用下，受到阻力矩。设为盖板的转动惯量，则由牛顿第二定律，有：

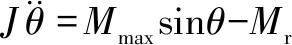
(13)

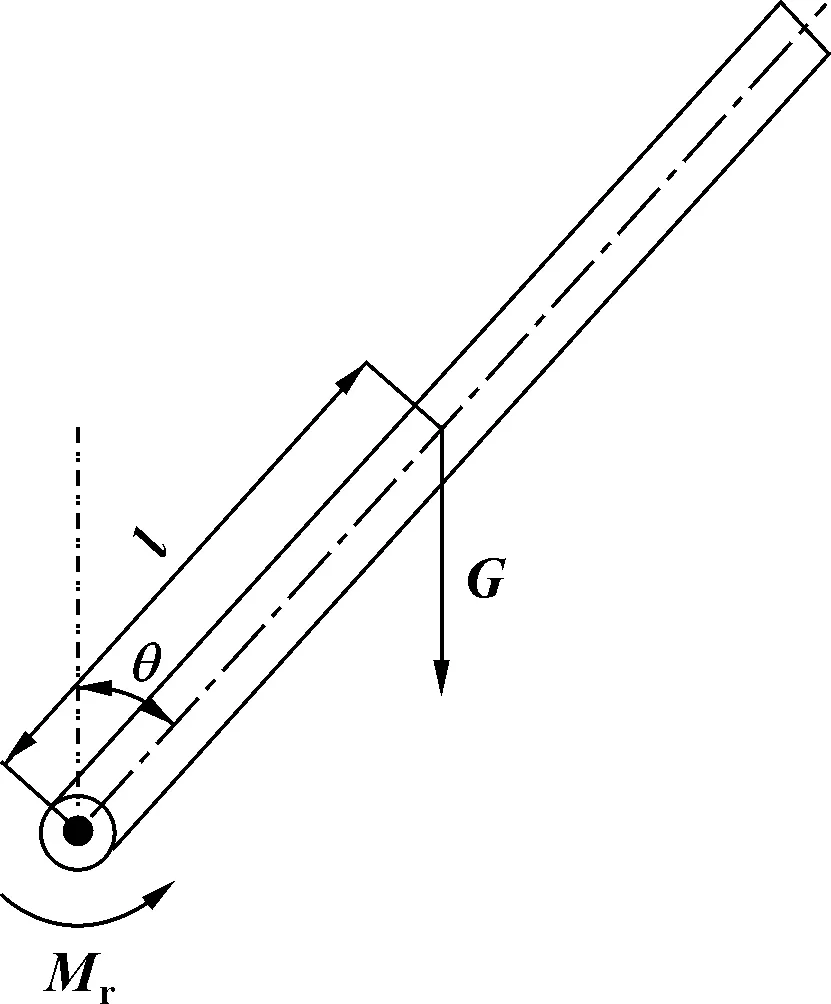
图8 盖板下落受力分析

结合式(1)(2)(8)(9)(12)得旋转阻尼器输出的阻力矩为

(14)

结合式(13)(14)，对于盖板下落的过程，可列出下列方程组:

(15)

对于式(15)，可在Python中编写程序,采用龙格-库塔法进行求解。通过设定初始下落角度、角速度，计算盖板在旋转阻尼器的作用下下落不同时间对应的下落角度与角速度，从而得到旋转阻尼器系统的性能。

2 参数匹配分析

盖板旋转阻尼器系统的下落特性包括盖板下落角度达到90°与底面发生冲击时的角速度与下落所用的时间。为避免损害盖板结构并增加产品的实用性，在参数匹配设计时应使冲击角速度较低、下落时间较短。

以某旋转阻尼器系统为例，其结构参数如表1所示。

表1 旋转阻尼器系统结构参数

对于该系统，首先应校核凸轮结构是否会发生自锁。===0.04，由摩擦角的定义有===2.29°，通过式(7)计算得不发生自锁时的取值范围为4.58°<<85.41°。由式(3)计算得=63.32°，满足不发生自锁的条件。

由式(15)可知，凸轮的结构参数、弹簧刚度与阻尼系数都会影响盖板旋转阻尼器系统的下落特性。由于凸轮的参数影响旋转阻尼器的总体安装尺寸，在匹配旋转阻尼器时，一般不改变凸轮的结构参数，而是通过选择适当的弹簧与黏滞阻尼器参数来达到所需的性能。

取不同的弹簧刚度与黏滞阻尼器阻尼系数，计算盖板从35°自行下落至90°时盖板的冲击角速度，并以弹簧刚度为横坐标、阻尼系数为纵坐标，绘制盖板冲击角速度等高线如图9所示。可知：随着弹簧刚度与阻尼系数的增加，冲击角速度减小。可根据该等高线图匹配弹簧刚度与阻尼系数，得到所需的冲击角速度。根据式(11)，在匹配弹簧时还应使<18 851 N/mm，以确保盖板可自行下落。

图9 不同冲击角速度时弹簧刚度和阻尼系数的关系

不同的弹簧与黏滞阻尼器参数的组合也可以达到相同的冲击角速度。根据图9取冲击角速度相同的弹簧刚度与黏滞阻尼器阻尼系数组合，绘制盖板下落的时间-下落角度曲线，如图10所示。

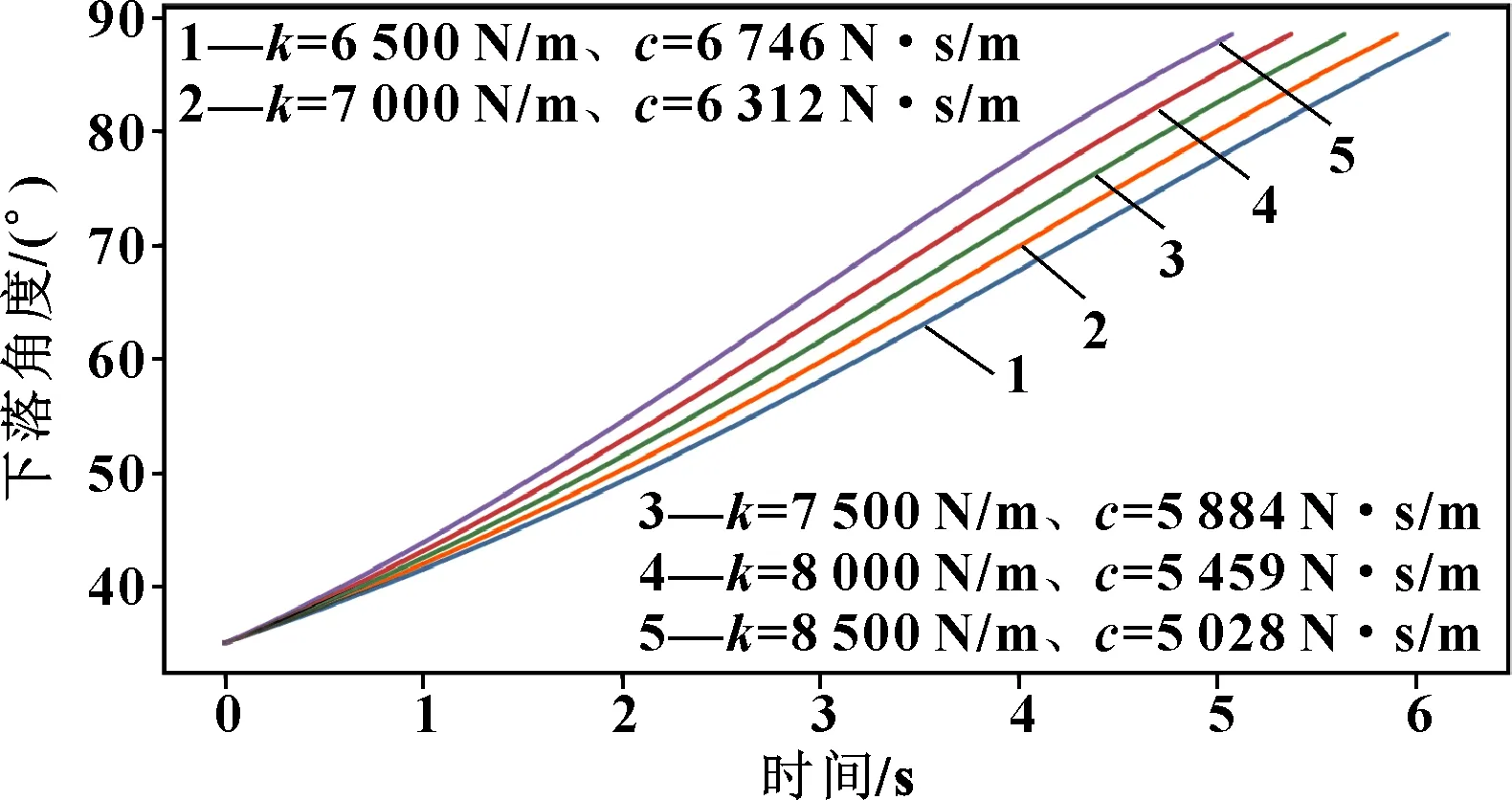
图10 不同弹簧-黏滞阻尼器参数组合下的盖板时间-下落角度曲线

由图10可知：在冲击角速度相同时，低弹簧刚度、高阻尼系数组合的盖板下落时间较长；高弹簧刚度、低阻尼系数组合的盖板下落时间较短。因此，选择弹簧刚度较高、阻尼系数较低的组合有利于提升旋转阻尼器系统的性能。

3 实验

以表1所示的旋转阻尼器作为实验对象，选择刚度为7 056 N/m的弹簧，阻尼系数为6 817 N·s/m的黏滞阻尼器。在下落角度为35°的位置使盖板下落，使用角位移传感器与力矩传感器记录盖板下落的角度与旋转阻尼器输出的力矩，并将它们与通过第1节所述的理论模型计算得到的结果进行对比，结果如图11所示。

图11 实验结果与计算结果对比

根据图11(a)，实验与理论计算的时间-下落角度曲线较为一致。盖板下落至90°的实际时间为7.33 s，较理论计算结果6.85 s，相对误差为7.01%，可见该动力学理论计算模型用来计算旋转阻尼器系统的性能具有较高的准确性。在盖板下落的0～2 s的时间内，时间-下落角度曲线的理论与实验结果有差异，结合图11(b)可知，这是因为在黏滞阻尼器输出模型中未考虑到黏滞阻尼器的刚度特性。