基于Excel的模拟程序在生化反应工程课程教学中的应用

陈翰驰,陆跃乐,朱林江,陈小龙

(浙江工业大学 生物工程学院,浙江 杭州 310014)

生化反应工程是一门建立在反应工程学科基础之上,结合生化反应特有的过程(如酶催化、微生物生长和细胞代谢等)所形成的具有生物工程专业特色的课程[1-2]。该课程侧重于研究生化反应过程中反应速率的变化规律以及不同类型反应器对于生化反应过程的影响,研究内容兼具理论性和实践性,对学生理解生化反应机制、控制生化反应过程和设计生化反应设备等一系列工程理论和实践能力的培养具有重要意义[3-5]。生化反应工程作为工科专业课程要求学生能够灵活将所学理论知识用于解决工程实际问题,然而该课程在实际教学过程中往往会遇到复杂的动力学计算问题,导致学生难以理解理论内容,更限制了理论知识的实践应用,容易导致理论脱离实践的教学情况。针对生化反应工程课程教学中涉及的复杂计算问题,笔者提出采用一种基于Excel VBA开发的程序,方便教学中展示动力学分析过程中的数据计算和拟合问题,有助于加深学生对反应工程理论知识的理解,提升学生对课程学习的兴趣,符合成果导向的教育理念[6],丰富了课程的多元化教学模式[7]。

1 生化反应工程课程中的复杂计算问题

生化反应工程课程教学内容通常分为基础理论教学部分和理论应用部分。其中,对于理论基础的教学以化学反应基础出发,内容包括对基元反应、阿伦尼乌斯定律、快速平衡假设和拟稳态假设等内容的学习,帮助学生理解影响反应速率的因素,并掌握反应速率方程的推导方法;对于理论应用的教学内容则是结合理论所得的反应速率方程,对该反应在不同类型反应器(间歇式反应器、平推流反应器、全混流反应器)中动力学过程进行分析[8],从而实现反应工艺合理设计以及反应器合理选型,帮助学生通过理论解决实际工程问题。

生化反应相较于化学反应往往具有更为复杂的反应过程,其动力学过程所受的影响因素也更多[9],因此生化反应过程的速率方程通常较为复杂,这为分析实际反应器中的生化反应动力学过程提出了难题,造成学生在学习反应工程课程时难以应用所学习的理论知识,认为课程内容实用性不强,从而影响学习兴趣。以细胞培养过程为例,法国科学家莫诺所提出的莫诺方程(Monod equation)可以很好地描述细胞生长的动力学过程[10],莫诺认为细胞的生长速率受培养基中底物质量浓度的影响,其比生长速率(Specific growth rate,μG)公式为

(1)

式中:μmax为最大比生长速率;KS为半饱和常数;S为限制性底物的质量浓度。根据莫诺方程可进一步得到培养基中的细胞生长速率(rX),其表达式为

(2)

式中X为细胞质量浓度。可见式(2)中受到2个体系变量影响,分别为培养基中的细胞质量浓度和限制性底物的质量浓度。因此,细胞生长的动力学过程还需结合底物消耗过程进行计算,底物消耗的动力学过程(rS)计算式为

(3)

式中YFX/S为细胞对于底物的产出率。

从工程应用的角度来讲,当明确该细胞生长特征时(已知μmax,KS,YFX/S),理论上可得到该细胞生长的动力学过程,从而实现对种子罐的设计和选型。然而,由于该动力学过程的分析涉及到对式(2,3)进行二元微分方程求解,计算难度较高,导致学生难以将动力学理论应用于实际工程问题的解决上。类似的多元微分方程的计算问题,在复杂酶催化动力学过程过程以及生物反应器设计中均有涉及[11-13]。此外,如何结合动力学方程与实验数据分析得到某个生化反应过程的动力学参数,从而对该生化反应过程进行动力学分析及工艺设计,也是该课程教学过程中的难点。

通过计算机软件辅助计算可有效解决上述问题。如美国MathWorks公司所开发的Matlab软件可以实现多元微分方程的积分求解[14];Aspen Plus设计仿真软件可在知晓反应过程动力学参数的前提下对反应器进行智能选型和设计[15]。然而,上述软件对于生物工程本科学生来讲并不常用,对于这些软件的熟练运用也需要系统性的教学,受课时限制,这些软件的使用方法不适合在生化反应工程这门课程中进行讲解。对此,笔者开发了基于Excel的模拟程序,用于解决复杂生化反应过程中的动力学计算问题。由于软件本体常用,操作过程简单,适用于生化反应工程课程的教学。

2 基于Excel的生化反应过程模拟程序

生化反应体系通常会遇到较为复杂的反应动力学过程,如细胞培养的动力学过程涉及到多元微分方程的计算,此外细胞代谢过程中的串联反应、受产物影响的酶促反应和发酵过程等重要生化反应过程,均涉及到类似的多元微分方程的计算问题,且生化反应过程的动力学研究在生化反应工程的本科教育中至关重要。对此,笔者基于Excel中的VBA模块进行编程,所得程序可直接在学生个人电脑中通过Excel打开使用,能够有效用于解决生化反应过程中的动力学计算问题,一方面可以实现对生化反应过程的模拟及动力学分析;另一方面可以培养学生多学科交叉的学习意识和能力[16]。

该程序的计算原理基于瑞士著名数学家莱昂哈德·欧拉提出的差分法计算多元微分方程,当已知某反应的速率方程时,可通过差分法从反应原始状态出发,计算得到任意反应时间后反应器内的物质状态[17]。仍以细胞培养为例,根据莫诺方程可以得到细胞生长和底物消耗的速率式(2,3),由于在培养开始时(t0)培养基中的底物初始量(S0)与接种量(X0)是已知的,可以通过速率方程计算得到在经过很短的时间后(t1=t0+Δt)培养基中底物(S1)与细胞的量(X1),其表达式分别为

S1=S0+rSΔt

(4)

X1=X0+rXΔt

(5)

依次按照时间迭代,可以得到任意时间底物与细胞质量浓度情况。该方法将繁琐的多元微分方程转化为多元方程组进行求解,实现了计算过程的简化。该计算过程以编写为基于VBA的计算程序如图1所示,学生只需通过Excel打开已编辑完成的程序,输入对应的速率方程,即可完成该反应动力学过程的计算。当动力学参数确定时,所得到的计算结果即能模拟该反应的动力学过程。图1中的程序是使用在Sub与End Sub之间可输入多个多元微分方程进行计算,程序公式中的c代表常数;y代表变量。

图1 动力学方程在模拟程序中的输入界面Fig.1 Equation input interface in the simulation program

3 VBA模拟程序的应用

3.1 反应动力学过程分析的应用

反应工程对于工业生产中的过程监控以及反应器的设计选型具有重要的指导作用[18]。当知晓某反应过程的动力学参数时,理论上可以得到该反应的动力学过程,然而在实际计算过程中往往会遇到困难,需要借助计算机辅助计算,而上述模拟程序可以帮助生物工程专业本科学生在已有的计算机基础上完成生化反应动力学过程的辅助计算,从而在一方面帮助学生更加直观地分析该反应的过程特征,把握该反应的限制性因素;另一方面有助于学生将动力学分析运用于生化反应器的设计过程中。

以第1节细胞培养过程为例,模拟酿酒酵母(S.cerevisiae)以葡萄糖为底物,在温度为30 ℃下进行有氧培养过程,通过研究已知该过程的动力学参数μmax=0.55 h-1,KS=0.025 g/L,YFX/S=0.5 g/g。因此可通过物料衡算分析S.cerevisiae在间歇式反应器中细胞生长与底物消耗的动力学过程,其表达式分别为

(6)

(7)

式中:下标pcf表示过程细胞进料;下标pcd表示过程细胞出料。

将式(6,7)输入VBA模拟程序,可以得到S.cerevisiae在间歇式反应器中的培养动力学过程,其动力学曲线如图2所示(实线表示接种量为1 g/L;虚线表示接种量为2 g/L)。由此可知:通过该程序可计算得到任意培养时间在培养基中的细胞质量浓度和底物质量浓度。通过模拟计算结果可对酿酒酵母细胞的培养工艺进行设计和并对培养设备进行选型。

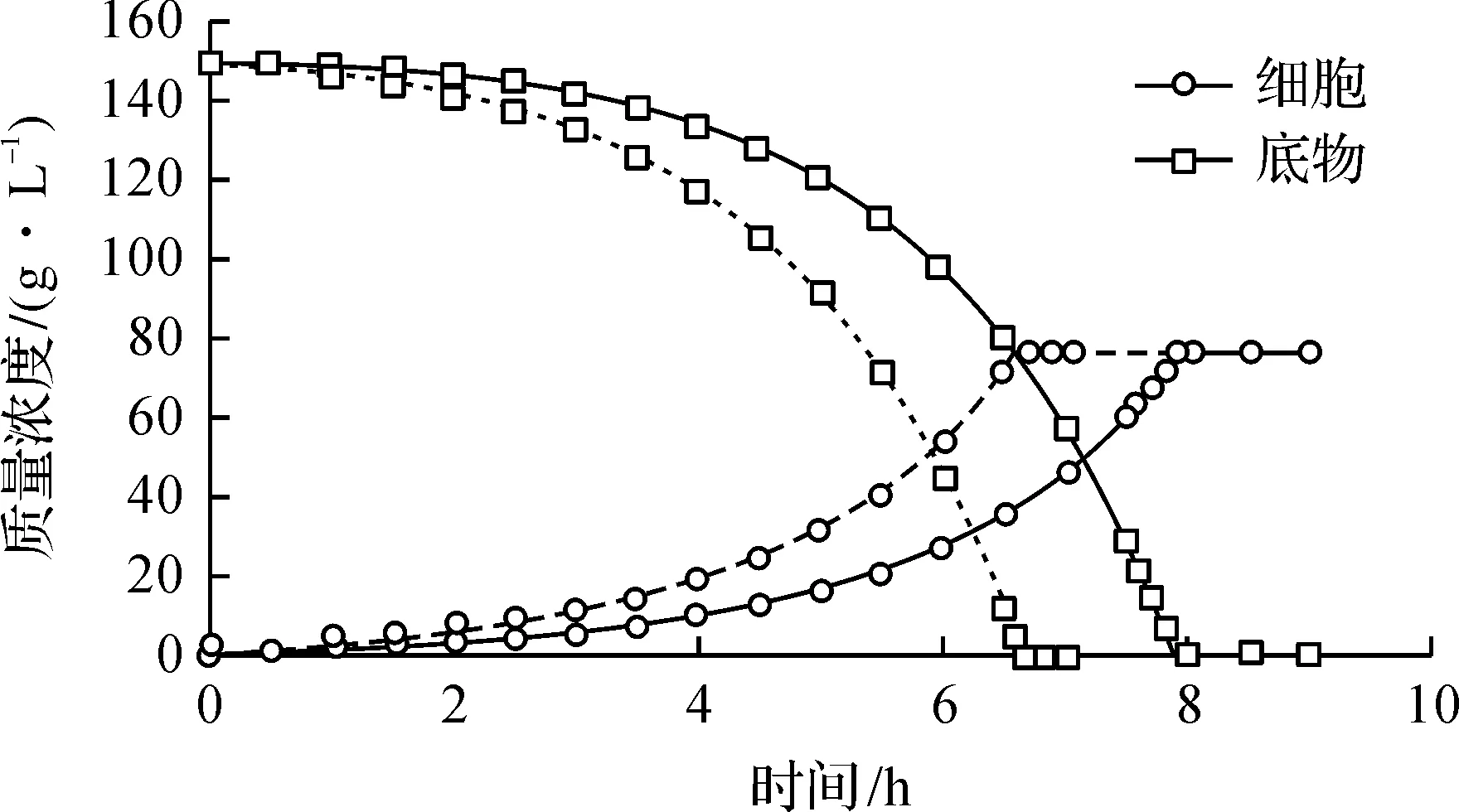
图2 S.cerevisiae细胞培养的动力学过程Fig.2 Simulation of the S.cerevisiae growth kinetics with the program

从图2中实线曲线可以看出:该培养体系在接种7.9 h后可实现底物的完全转化,并得到对应的细胞质量浓度,对应到工程设计案例,如酵母粉生产厂家,学生可根据生产目标及动力学模拟结果,结合准备与后处理过程,确定所需罐体的个数与体积,完成对细胞培养工段进行设计。此外,在该程序辅助计算的帮助下,学生可根据实际生产需求对工艺进行调整。例如,对于产量需求较高的厂家来讲,可以通过提高原始接种量缩短培养周期。从图2中虚线曲线可以看出:当接种量提升至2 g/L时,生产周期由原来的7.9 h缩短至6.7 h,可见模拟程序能够根据已知的动力学参数计算由式(6,7)组成的多元微分方程组,并用于分析不同培养条件下的细胞培养动力学过程。学生可通过该程序得到的模拟结果对设计工艺进行调整。

由上述可知:当已知某反应的动力学参数时,该程序可有效实现对该反应过程的模拟。由于生化反应工程往往面临着复杂反应过程的动力学分析,该程序对于生物工程专业学生具有较高的实用价值,有助于生物工程专业学生实现反应工程理论知识与实际工程问题之间的串联,从而提升学生对于反应工程课程的学习兴趣和工程问题的解决能力。

3.2 反应动力学参数拟合的应用

上述内容阐述了在已知动力学参数的情况下,利用所编写的程序对反应动力学过程进行模拟,并根据仿真结果确定反应工艺及反应设备。然而在更多的情况下,反应动力学参数是未知的,这就需要专业人员根据实验数据拟合获得动力学参数,从而实现反应规律的把握和对应的工艺设计[19]。这是反应工程理论在解决实际工程问题时的重要应用方式,也是生物工程专业学生所需掌握的专业技能。利用所编写的模拟程序结合Excel中的规划求解功能可实现反应过程动力学参数的拟合,拟合过程只涉及到Excel软件,生物工程专业学生可在已有的计算机基础上完成操作。以某甲基营养型微生物的生长过程为例,该微生物的生长动力学数据如表1所示,利用模拟程序拟合获得微生物生长动力学参数曲线如图3所示(虚线表示拟合前;实线表示拟合后),同样采用莫诺方程对该细胞培养过程进行分析,分析步骤如下:1) 在Excel表格中输入实验数据,并假设动力学参数;2) 在程序的VBA界面中输入动力学方程;3) 根据假设参数计算动力学数据,计算与实验数据之间的平方差,μmax=0.2 s-1,KS=0.2 g/L,YFX/S=0.3,对比结果见图3虚线曲线;4) 计算平方差之和,使用规划求解功能通过改变动力学参数求得平方差之和的最小值,实现动力学数据拟合,μmax=0.235 s-1,KS=1.3×10-6g/L,YFX/S=0.3,拟合曲线见图3实线曲线。由此可知:该方法能够结合模拟程序的初始计算结果与Excel中的规划求解功能实现动力学参数的有效拟合。

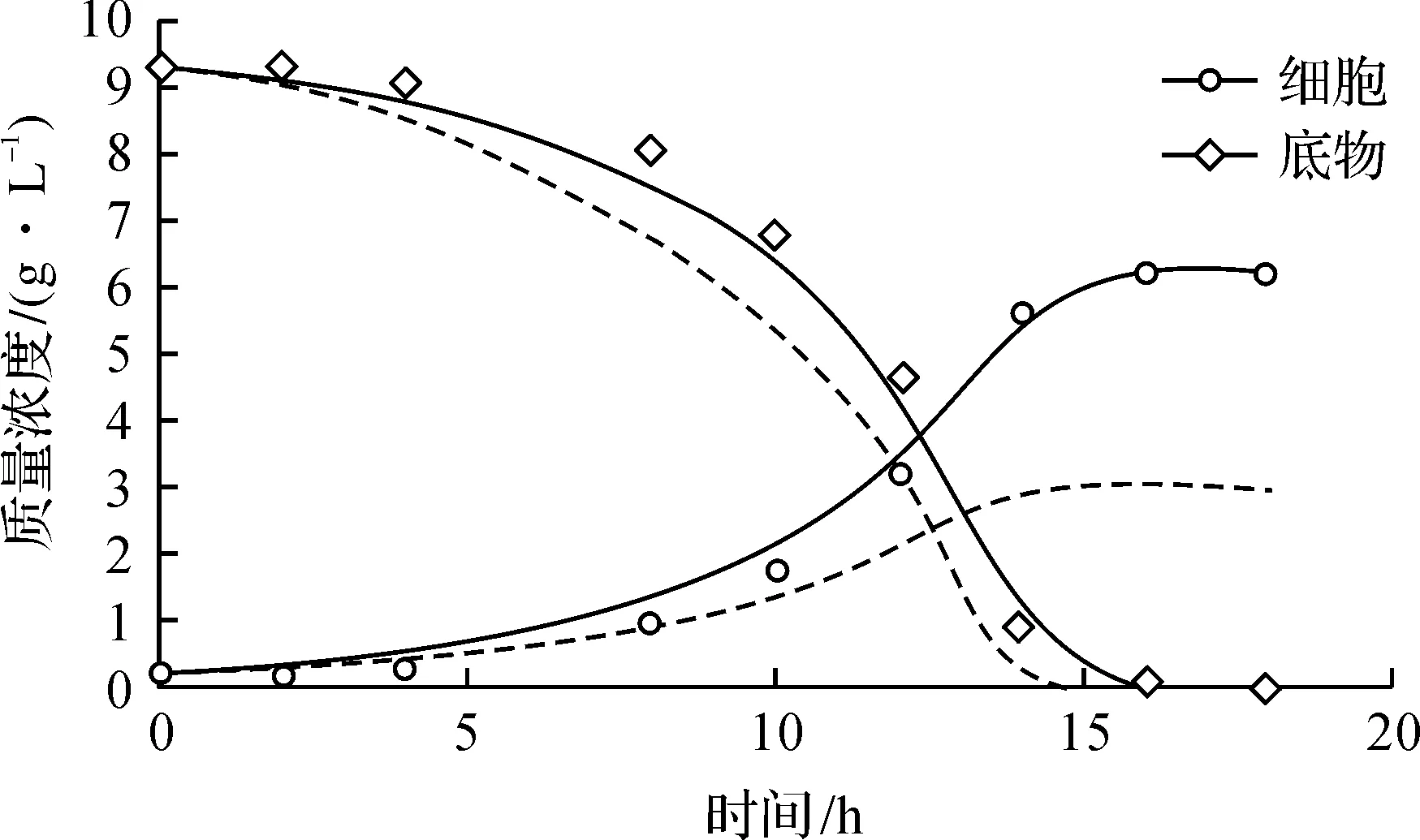
图3 利用模拟程序拟合获得微生物生长动力学参数Fig.3 To obtain the kinetics parameters with the simulation program through data fitting

4 实际教学应用与反馈

实际教学过程中,课程组运用该模拟程序结合工程问题进行案例式教学,学生们能够切身感受到反应工程理论知识在解决实际问题中的作用,极大程度调动了学生的学习积极性。例如,课程教学过程中给出如下简化的生物反应器设计问题:工厂希望通过间歇式发酵Streptococcuslactis得到L-乳酸以用于生产可降解塑料,已知发酵过程中限制性原料为葡萄糖,其初始质量浓度为30 g/L,初始接种量为0.5 g/L,发酵罐的准备时间(灭菌、加料和卸料)为3.5 h,发酵动力学参数:μmax=0.2 h-1,KS=0.2 mg/L,kd=0.002 h-1,YFX/S=0.4 g/g,μP=0.1μGh-1,请问最少需要多少发酵体积可达到100 kg的L-乳酸日产量?

该问题涉及反应过程优化和反应器容量设计,与实际生产过程联系密切,能够有效调动学生的学习兴趣。解决该问题涉及到莫诺方程式分别为

(8)

(9)

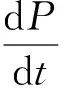
(10)

由式(8～10)联立求解,通过所开发的程序能够方便快速的得到的乳酸发酵动力学过程如图4所示。由图4可知:该过程发酵16.5 h时单位时间的乳酸产量最高,达到0.067 g/(L·h)。对应的24 h要达到100 kg的生产量需要62.5 m3的发酵体积。以往由于缺少有效的数学计算手段,相关实际问题的探讨在课程教学过程中难以展开。而在结合模拟程序后,学生能够有效实现反应工程理论知识和实践应用之间的串联,获得了学生的广泛好评。

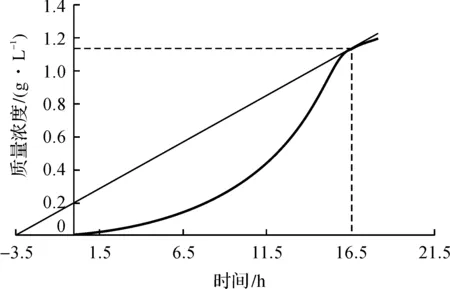
图4 模拟程序用于发酵工艺优化与反应器设计Fig.4 To obtain the L-lactic acid production process with thesimulation program and applied in reactor design

5 结 论

生化反应由于步骤与影响因素较为复杂,其动力学过程的分析涉及到复杂的数学计算,限制了学生对于反应动力学理论的理解和应用。采用计算机辅助软件虽然可有效解决相关数学计算问题,但由于软件本体不常见,学生缺乏相关计算软件的背景知识,软件的教学工作难以在课堂中展开。笔者提出采用基于Excel的模拟程序辅助解决生化反应工程课程教学中的复杂数学计算问题,软件本体常见,学生对软件的使用基础较好,且操作简单,适合应用于该课程的本科教学中。计算机辅助软件在课程教学中的结合不仅能够加深学生对生化反应工程的理解,而且能够提升学生对反应工程理论的应用能力,符合工科专业的教学要求。