非均匀二型三角剖分二元二次样条的数值积分公式
2022-09-17钱江王凡
钱江,王凡
(1.河海大学理学院,江苏 南京 211100;2.海岸灾害及防护教育部重点实验室(河海大学),江苏 南京 210098;3.南京农业大学理学院,江苏 南京 210095)
非均匀二型三角剖分二元二次样条的数值积分公式
钱江1,2,王凡3
(1.河海大学理学院,江苏 南京 211100;2.海岸灾害及防护教育部重点实验室(河海大学),江苏 南京 210098;3.南京农业大学理学院,江苏 南京 210095)
给出了构成矩形域的4个三角形子区域的二元样条拟插值算子的等价形式,对这4个三角形子区域分别建立了数值积分公式,相加后得到一般矩形域上的数值积分公式,同时给出了构造数值积分公式所需的结点处的函数值与相应的求积系数。进一步,利用算子范数、连续模及拟插值算子的保多项式性,针对具有不同连续性的被积函数,得到了相应的数值积分公式的求积余项。研究表明,提出的数值积分公式不仅具有较高的计算精度,而且计算量约为二元张量积型求积公式的1/5。数值算例进一步说明了数值积分公式的有效性。
多元样条;光滑余因子协调法;二元数值积分;样条拟插值; B网
0 引言
多元样条是研究多元数值逼近、计算几何、有限元等的重要工具。多元样条的研究方法除经典的张量积型B样条[1-2]、B网[3-4]外,光滑余因子协调法[5-6]值得关注。光滑余因子协调法可以确定多元样条函数空间维数,计算样条基函数[6-8],其中表示基于区域的任意三角剖分上具有阶光滑度的次多元样条函数空间。
事实上,借助光滑余因子协调法,多元样条的任何问题都能转化为求解等价的代数方程组。如文献[9-10]提出了具有最小局部支集的三次样条基函数。文献[11]提出了二型非均匀三角剖分上的样条函数空间。文献[12-13]建立了均匀二型三角剖分上的二元三次、四次样条函数空间及相应的样条拟插值算子。文献[14-16]研究了基于非均匀二型三角剖分的二元三次异度样条、样条拟插值及其导数逼近。文献[17]借助三角Gauss型求积公式,建立了具有圆形边界的凸多边形元上的低次代数数值积分。文献[18]利用四边形有限元给出了新的求积公式,并用B网方法计算得到凸四边形区域上的积分元素,结果表明其具有高精度。文献[19]根据带重节点在二型三角剖分上的二元二次B样条函数,推导了样条拟插值分层逼近方法,研究表明,其具有保多项式性与最优逼近性。文献[20-23]利用样条拟插值算子在具体算例中计算了数值积分。
主要研究内容如下:第1节给出子区域上样条拟插值算子的等价表达式;第2节利用样条基函数的B网系数构造数值求积公式;第3节基于样条拟插值算子范数与连续模,分别推导被积函数具有连续性的求积余项;第4节给出数值算例。
1 子区域上样条拟插值算子的等价表达式
计算得到,八边形支集4个拐角处的三角域上样条函数满足:
用虚线将4个拐角处的三角域一分为二,如图1所示,相应的曲面片记为,。这样在4个拐角处的三角域上曲面片分别具有统一的表达式[6]。
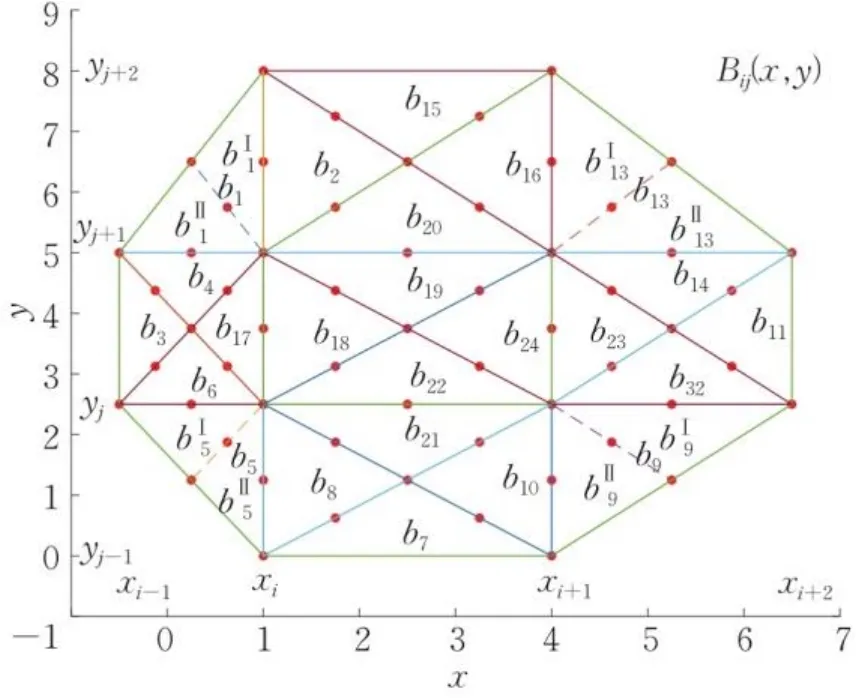
图1 的最小八边形支集Fig.1 Minimal octagonal support of
的二型三角剖分。采用文献[24-25]构造的样条拟插值算子:
得到
其中,
注1式(3)也可写为
定理1[20-21]对任意的,有
定理2对任意的样条拟插值算子可表示为
定理3对任意的样条拟插值算子可表示为
定理4对任意的样条拟插值算子可表示为
定理5对任意的样条拟插值算子可表示为
2 子区域上基于样条拟插值的数值积分
借助于面积坐标系,二元二次多项式在三角域上的数值积分可转化为B网系数之和与三角形面积的乘积[6],有
引理1设面积坐标系下的二元二次多项式为
则有
定理6三角域上的数值积分公式为
事实上,由式(9),可得二重积分:
表1 与样条函数对应的和
Table 1andcorresponding to the splines
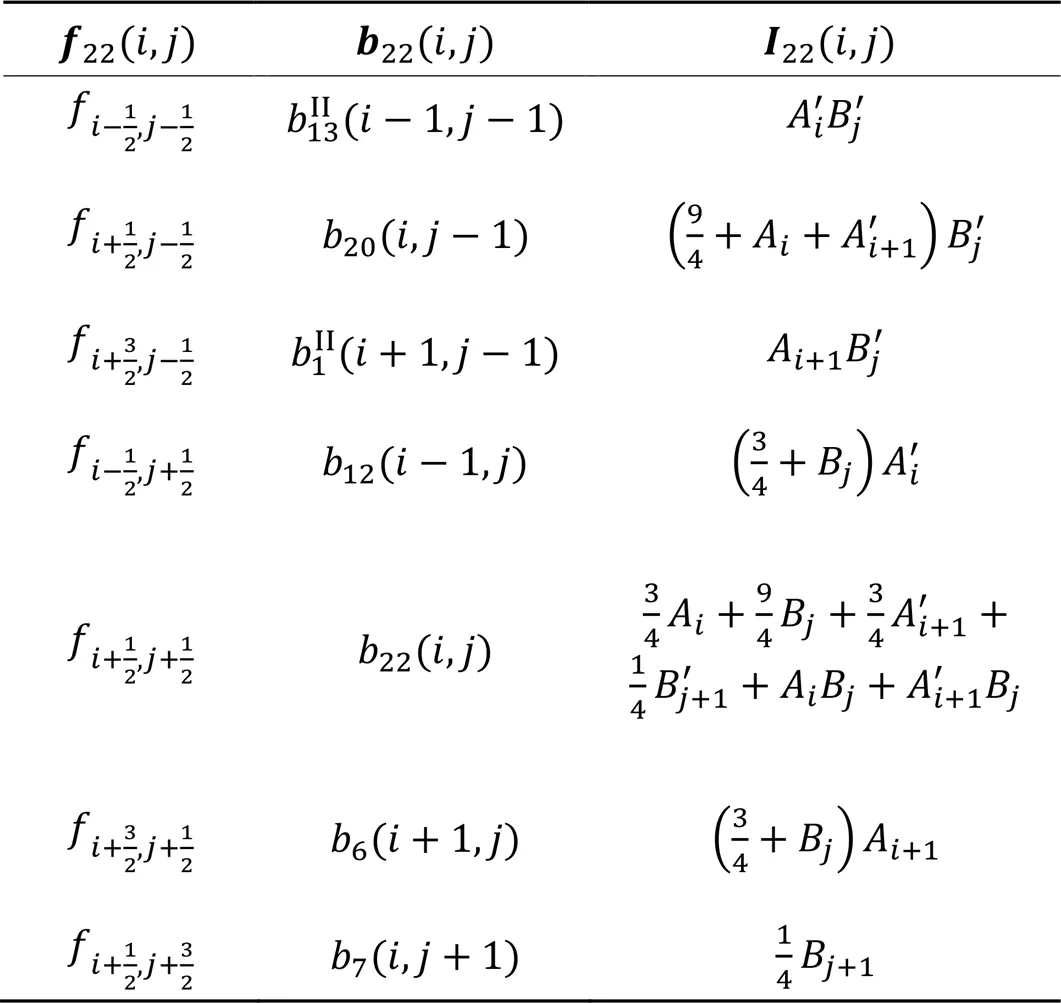
定理7三角域上的求积公式为
表2 与样条函数对应的和
Table 2andcorresponding to the splines
定理8三角域上的求积公式为
表3 与样条函数对应的和
Table 3andcorresponding to the splines
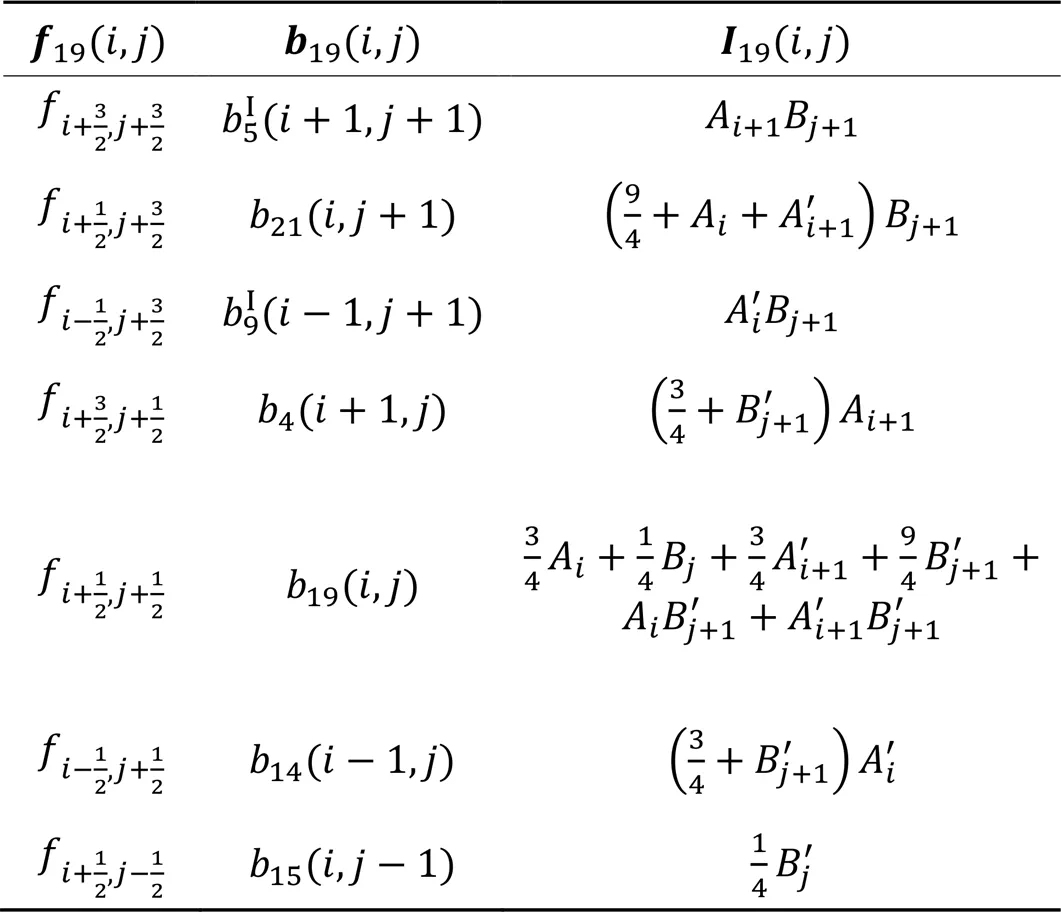
定理9三角域上的求积公式为
表4 与样条函数对应的和
Table 4andcorresponding to the splines
结合表1~表4,整理得到
定理10诸矩形子区域上的求积公式为
表5及其对应的
Table 5and its corresponding

注2由于式(6)具有保多项式性,因此,式(25)对任意的精确成立。
在计算量上,式(21)~式(24)均需9次乘法和8次加减法,式(25)需11次乘法和8次加减法,因此,矩形域上的数值积分共需次乘法和次加减法。为便于说明,绘制了矩形域在4个拐角处的非零B样条的最小八边形支集,如图2所示,将八边形支集自左至右、自上至下平移,得到每个三角形子区域上的所有非零B样条基函数。另外,如果采用矩形域上张量积型二元二次样条函数构造数值积分公式,则需利用代数方法精确确定求积系数,计算量较大。如对于张量积型B样条,其数值积分需次乘法和次加减法。可见,本文构造的矩形域数值积分公式的总计算量约为基于张量积型B样条求积公式计算量的1/5。
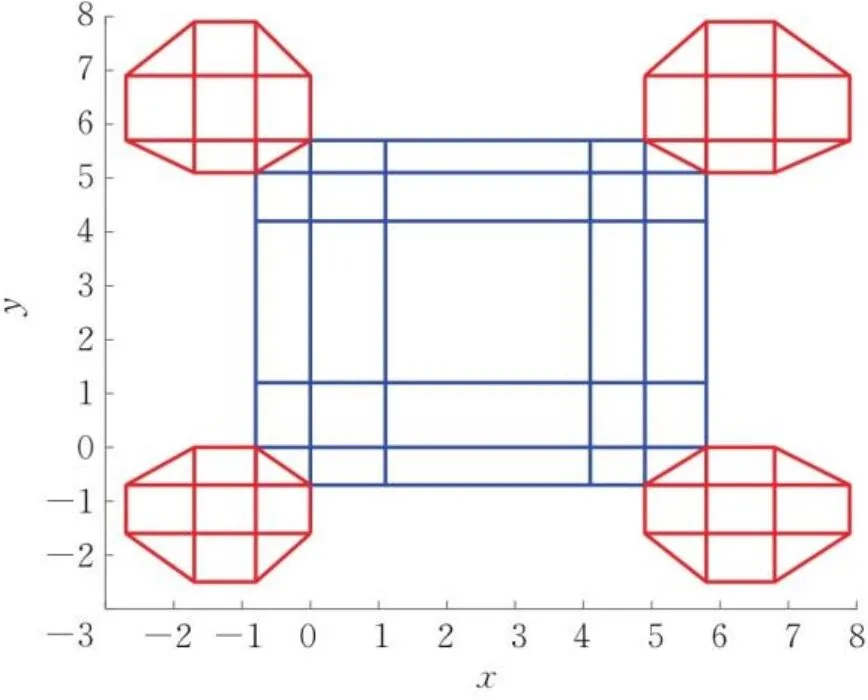
图2 矩形域上八边形支集的平移过程Fig.2 Translation process of the octagonal support over rectangular domain
3 数值积分公式的求积余项
定理11(i)若函数,则对充分大的正整数,有
证明 对于情形(i),根据B样条基函数的单位分解性,对任意的有
有
由此,结合算子范数,推得
因此,由定理11,对被积函数具有不同光滑性的数值积分,推导相应的求积余项。
定理12设表示矩形域的面积,当充分大时,有:
对所有i,j求和,可得矩形域上的求积余项:
对所有i,j求和,可得矩形域上的求积余项:
证毕。
4 数值算例
算例1设函数非均匀剖分上x方向的节点为y方向的节点为矩形胞腔中点处的横坐标分别为0.03,0.075,0.15,0.30,0.50,0.65,0.80,纵坐标分别为0.04,0.08,0.20,0.35,0.45,0.525,0.625,由此计算49个中点处的函数值。
由定理10可知,计算每个小矩形胞腔上的数值积分需要与此胞腔相邻的9个胞腔中点处的函数值,因此需计算矩形域上每个小矩形胞腔上的数值积分。将中点纵坐标为的5个矩形胞腔分别称为第层,得到数值积分近似值,按MATLAB二重积分程序dblquad计算真值,结果如表6所示。

表6 算例1数值积分的真值、近似值与误差Table 6 The real values,approximating values and error estimation of the numerical cubature in example 1
算例2设函数定义域与矩形剖分同算例1,同理计算近似值、真值及误差,结果如表7所示。

表7 算例2数值积分的真值、近似值与误差Table 7 The real values,approximating values and error estimation of the numerical cubature in example 2
本文所构造的二元二次样条的数值积分公式不仅具有良好的保多项式性,而且计算量小。另外,由于非均匀三角剖分二元二次样条表达式的复杂性,直接用传统的样条函数计算拟插值,进而计算数值积分的计算量非常大,且计算过程冗长。采用B网系数可大大简化计算过程。进一步可将二元数值积分公式应用于浅水动力学模型的求解,研究非均匀三角剖分的三次样条数值积分问题。
感谢特拉华州立大学Shi Xiquan教授与匿名审稿专家提出的宝贵意见和建议。
[1]SCHUMAKER L L. Spline Functions:Basic Theory[M]. Malabar,FL: Krieger Publishing Company,1993.
[2]王国瑾,汪国昭,郑建民. 计算机辅助几何设计[M]. 北京:高等教育出版社,2001.
WANG G J, WANG G Z,ZHENG J M. Computer Aided Geometric Design[M]. Beijing: Higher Education Press,2001.
[3]FARIN G. Triangular Bernstein-Bézier patches[J]. Computer Aided Geometric Design, 1986,3(2): 83-127. DOI:10.1016/0167-8396(86)90016-6
[4]FARIN G. Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide[M]. San Diego: Academic Press Professional,1993.
[5]王仁宏. 多元齿的结构与插值[J]. 数学学报, 1975,18(2): 91-106.
WANG R H. Structure and interpolation of multiple teeth[J]. Acta Mathematica Sinica, 1975,18(2): 91-106.
[6]WANG R H. Multivariate Spline Functions and Their Applications[M]. Beijing: Science Press/ Dordrecht:Kluwer Academic Publishers, 2001.
[7]SHI X Q. The singularity of Morgan-Scott triangulation[J]. Computer Aided Geometric Design, 1991,8(3): 201-206. DOI:10.1016/0167-8396(91)90002-S
[8]XU Z Q, WANG R H. The instability degree in the dimension of spaces of bivariate spline[J]. Analysis in Theory and Applications, 2002,18(1): 68-80. DOI:10.1007/BF02837049
[9]WANG S M. Spline interpolations over type-2 triangulations[J]. Applied Mathematics and Computation, 1992,49(2/3):299-313. DOI:10. 1016/0096-3003(92)90031-U
[10]WANG S M, WANG C L. Smooth interpolations on some triangulations[J]. Utilitas Mathematica, 1992, 41:309-317.
[11]LIU H W, HONG D,CAO D Q. Bivariatecubic spline space over a nonuniform type-2 triangulation and its subspaces with boundary conditions[J]. Computers and Mathematics with Applications, 2005,49(11/12):1853-1865. DOI:10.1016/j.camwa.2004.08.014
[12]LI C J, WANG R H. Bivariate cubic spline space and bivariate cubic NURBS surfaces[C]// Proceedings of Geometric Modeling and Processing 2004. Beijing: IEEE,2004:115-123. DOI:10.1109/GMAP.2004. 1290033
[13]WANG R H, LI C J. Bivariate quartic spline spaces and quasi-interpolation operators[J]. Journal of Computational and Applied Mathematics, 2006,190(1): 325-338. DOI:10.1016/j.cam.2004.11.052
[14]QIAN J, WANG F. On the approximation of the derivatives of spline quasi-interpolation in cubic spline space[J]. Numerical Mathematics Theory Methods and Applications, 2014,7(1): 1-22. DOI:10.4208/nmtma.2014.y12035
[15]QIAN J, WANG R H,LI C J. The bases of the non-uniform cubic spline space[J]. Numerical Mathematics: Theory,Methods and Applications, 2012,5(4): 635-652. DOI:10.1017/S10048979 00001094
(下转第页)
QIAN J, WANG R H,ZHU C G, et al. On spline quasi-interpolation in cubic spline space[J]. SCIENTIA SINICA Mathematica, 2014, 44(7):769-778. DOI:10.1360/N012013-00140
[17]ARTIOLI E, SOMMARIVA A,VIANELLO M. Algebraic cubature on polygonal elements with a circular edge[J]. Computers and Mathematics with Applications, 2020,79(7): 2057-2066. DOI:10. 1016/j.camwa.2019.10.022
[18]HU Q Y, XIA Y,HU P, et al. A concave-admissible quadrilateral quasi-conforming plane element using B-net method[J]. European Journal of Mechanics-A/Solids, 2016,57: 34-44. DOI:10. 1016/j.euromechsol.2015.12.001
[19]LAMBERTI P, SAPONARO A. Multilevel quadratic spline quasi-interpolation[J]. Applied Mathematics and Computation, 2020,373: 125047. DOI:10.1016/j.amc.2020.125047
[20]DAGNINO C, LAMBERTI P. On the approximation power of bivariate quadraticsplines[J]. Journal of Computational and Applied Mathematics, 2001,131(1): 321-332. DOI:10.1016/S0377-0427(00)00265-X
[21]DAGNINO C, LAMBERTI P. Some performances of local bivariate quadraticquasi-interpolating splines on nonuniform type-2 triangulations[J]. Journal of Computational and Applied Mathematics, 2005,173(1): 21-37. DOI:10.1016/j.cam.2004.02.017
[22]DAGNINO C, REMOGNA S. Quasi-interpolation based on the ZP-element for the numerical solution of integral equations on surfaces in[J]. BIT Numerical Mathematics, 2017, 57:329-350. DOI:10.1007/s10543-016-0633-x
[23]LAMBERTI P. Numerical integration based on bivariate quadratic spline quasi-interpolants on bounded domains[J]. BIT Numerical Mathematics, 2009, 49:565-588. DOI:10.1007/s10543-009-0237-9
[24]WANG R H, LU Y. Quasi-interpolating operators and their applications in hypersingular integrals[J]. Journal of Computational Mathematics, 1998,16(4): 337-344.
WANG R H, LU Y. Quasi-interpolating operators inon non-uniform type-2 triangulations[J]. Numerical Mathematics: A Journal of Chinese Universities,1999(2): 97-103.
[26]WANG G, LIANG Q H,ZHENG J H. A new multilayer nonhydrostatic formulation for surface water waves[J]. Journal of Coastal Research, 2019,35(3): 693-710. DOI:10.2112/JCOASTRES-D-18-00022.1
Numerical integration formulas of bivariate quadratic splines upon non-uniform type-2 triangulation
QIAN Jiang1,2, WANG Fan3
(1. College of Science,Hohai University,Nanjing211100,China;2. Key Laboratory of Coastal Disaster and Defence(Hohai University),Ministry of Education,Nanjing210098,China;3. College of Science,Nanjing Agricultural University,Nanjing210095,China)
In the paper, equivalent representations of the spline quasi-interpolation are presented over four triangular sub-domains contained in a general rectangular domain. Moreover, the direct bivariate numerical integration formulas are constructed over the four triangular sub-domains, while summing them yields the integration formula over the general rectangular domain. For illustration, the necessary function values and the corresponding integration coefficients are listed in several tables. Furthermore, based on the norm of the operator, the module of continuity and the reproduction of bivariate polynomials, error estimations of the numerical integration are derived for continuously differential functions with different orders. The computational cost of the proposed method is approximately 1/5 of that based on tensor-product-type quadratic splines. Numerical examples show the validity of the proposed numerical integration approach.
multivariate spline; conformality of smoothing cofactor method; bivariate numerical integration; spline quasi-interpolation; B-net
O 241.5
A
1008⁃9497(2022)05⁃555⁃09
2021⁃04⁃06.
江苏省自然科学基金青年基金项目(BK20160853);河海大学中央高校基本科研业务费项目(2019B19414);海岸灾害与防护教育部重点实验室开放基金项目(河海大学202011);国家留学基金资助出国留学项目(访问学者201806715010).
钱江(1981—),ORCID:https://orcid.org/0000-0002-0526-5660,男,博士,副教授,主要从事数值逼近与计算几何研究,E-mail:qianjianghhu@sina.com.
10.3785/j.issn.1008-9497.2022.05.006
