具有混合隔离策略的非线性计算机病毒传播模型的Hopf分岔研究

杨芳芳，张子振

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030）

具有混合隔离策略的非线性计算机病毒传播模型的Hopf分岔研究

杨芳芳，张子振*

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030）

建立了考虑潜伏期时滞和临时免疫期时滞的具有混合隔离策略的非线性计算机病毒传播模型，旨在帮助理解计算机病毒在网络中的传播规律。通过计算模型基本再生数，以不同时滞组合为分岔参数，研究了模型的局部渐近稳定性；利用中心流形定理和规范型理论分析了Hopf分岔的方向和周期解的稳定性，并通过数值模拟验证了理论分析的正确性。研究结果可为计算机病毒治理提供理论依据。

混合隔离策略；时滞； Hopf分岔；数值模拟

据中国互联网络信息中心（CNNIC）发布的第49次《中国互联网络发展状况统计报告》，截至2021年12月，我国网民规模达10.32亿，互联网普及率达73.0%［1］。互联网的广泛应用在方便人们工作生活的同时，也带来了巨大的安全隐患。一些病毒以热点信息为诱饵，攻击企事业单位或个人的电脑，例如，以新冠肺炎疫情为题材传播的DTLMiner病毒、以防疫为题材传播的Sidewinder病毒等，严重威胁了用户的网络安全。近年来，计算机感染病毒事件层出不穷。国家信息中心联合瑞星公司发布的《2021年中国网络安全报告》指出，2021年瑞星“云安全”系统共截获病毒样本1.19亿个，感染病毒2.59亿次，病毒总数较2020年同期下降了19.66%［2］。虽然杀毒软件在防御计算机病毒方面具有一定成效，但更新总是滞后于新病毒传播，因此，建立合适的数学模型［1］研究计算机病毒的传播规律十分必要。

自1991年KEPHART等［3］将生物病毒研究中的数学模型引入计算机病毒研究以来，已建立了各种数学模型，用以研究计算机病毒的传播规律，较经典的有易感-感染-易感（susceptible-infectious-susceptible，SIS）模型［4-7］、易感-感染-恢复-易感（susceptible-infectious-recovered-susceptible，SIRS）模型［8-11］、易感-潜伏-感染-恢复（susceptible-exposed-infectious-recovered，SEIR）模型［12-16］等。通过引入多种实际因素，建立了更加贴合实际的模型。如AMADOR等［17］考虑免疫计算机通过发送警告信号减少病毒传播的特点，建立了随机SIRS模型，并分析了模型感染后的传播和持续性等主要指标，但未研究其稳定性。YANG等［18］针对传播网络的异构性，提出了一种基于异构节点的SIRS模型，并详细讨论了模型的全局稳定性，但在建模过程中没有考虑病毒传播的时滞因素。MADHUSUDANAN等［19］认为，计算机病毒与生物病毒类似，会随时间不断发展，最终感染系统或网络中的资源，即潜伏期时滞，并基于此提出了新的时滞SIRS计算机病毒传播模型，对模型局部渐进稳定性进行了研究。

上述模型均忽略了潜伏期对计算机病毒传播的影响。潜伏期是计算机病毒的显著特征。实际上，某些计算机病毒需执行一定的程序才会被激活，如果相关程序一直未被执行，则计算机病毒可长期潜伏，因此，在研究计算机病毒的传播规律时，应考虑潜伏期。另外，隔离策略作为预防计算机病毒传播的一项重要措施，不仅可以隔离感染源，还有利于控制感染的计算机，因此在建模过程中也应考虑隔离策略。

处于潜伏状态的病毒虽未爆发，但计算机某些程序会出现异常，如流量过大等。这些异常现象会被检测系统识别，因此病毒处于潜伏状态的计算机存在一定的被隔离风险。在研究计算机病毒传播的动力学原理时，有很多将时滞因素作为其重要影响因素，如MADHUSUDANAN等［19］在建模过程中考虑了潜伏期时滞，但忽略了临时免疫期时滞。通常，杀毒软件可使处于恢复状态的计算机在短时间内免受病毒感染，出现临时免疫期时滞。

本文在文献［19］的基础上，提出一类新的非线性计算机病毒传播模型，不仅考虑潜伏期和隔离策略，而且考虑临时免疫期时滞和混合隔离策略，更加贴合实际。详细探讨不同时滞条件下模型的局部稳定性及Hopf分岔，并采用仿真模拟对理论分析结果进行验证。

1 模型的提出

在文献［19］的基础上，综合考虑潜伏状态、隔离状态以及临时免疫期时滞，建立了具有混合隔离策略的非线性计算机病毒传播模型：

2 基本再生数

基本再生数是衡量系统中是否存在计算机病毒的重要阈值，由文献［19-20］的方法计算式（1）的基本再生数，令

进而有

3 有毒平衡点的稳定性和Hopf分岔存在性

其中，

相应的特征方程为

其中，

案例1当时，式（6）可转化为

其中，

引理1［19］根据Routh-Hurwitz定理，当式（7）的所有根均有负实部，即，，，，且时，式（1）在有毒平衡点处局部渐近稳定，其中，

案例2当时，式（6）可转化为

其中，

其中，

进而可得

其中，

其中，

假设1至少存在1个正根，使式（11）成立，那么

其中，

为方便计算，令

其中，

假设2若，则有毒平衡点局部渐近稳定［21］。可得

定理1对于式（1），如果假设1和假设2成立，那么，当时，式（1）局部渐近稳定；当时，式（1）在有毒平衡点处产生Hopf分岔。

案例3当时，式（6）可转化为

其中，

其中，

将式（16）中两个等式平方后相加，可得

假设3如果存在1个正根，使得式（17）成立，那么

通常取

假设4若，则有毒平衡点局部渐近稳定［21］。可得

定理2对于式（1），如果假设3和假设4成立，那么，当时，式（1）局部渐近稳定；当时，式（1）在有毒平衡点处产生Hopf分岔。

案例4当时，与案例2相似，不再赘述推导过程，可得

定理3对于式（1），在给定条件下，当时，式（1）局部渐近稳定；当时，式（1）在有毒平衡点处产生Hopf分岔。

5 Hopf分岔方向和周期解的稳定性

根据文献［22-23］，分析式（1）的Hopf分岔方向和周期解的稳定性。当，时，假设，，令，，，，，，式（1）可转化为

其中，

令

则式（1）可转化为

定理4当时，式（1）产生超临界Hopf分岔；当时，式（1）有稳定的分岔周期解；当时，式（1）的分岔周期递增。

6 数值模拟

基于MATLAB软件的DDE23算法进行数值模拟。综合考虑收敛速度及收敛结果的精度，固定步长设置为0.001。取，，，，，，，，，，，，，，示例模型为

图1 当时，局部渐近稳定

Fig.1 When，is local asymptotic stability

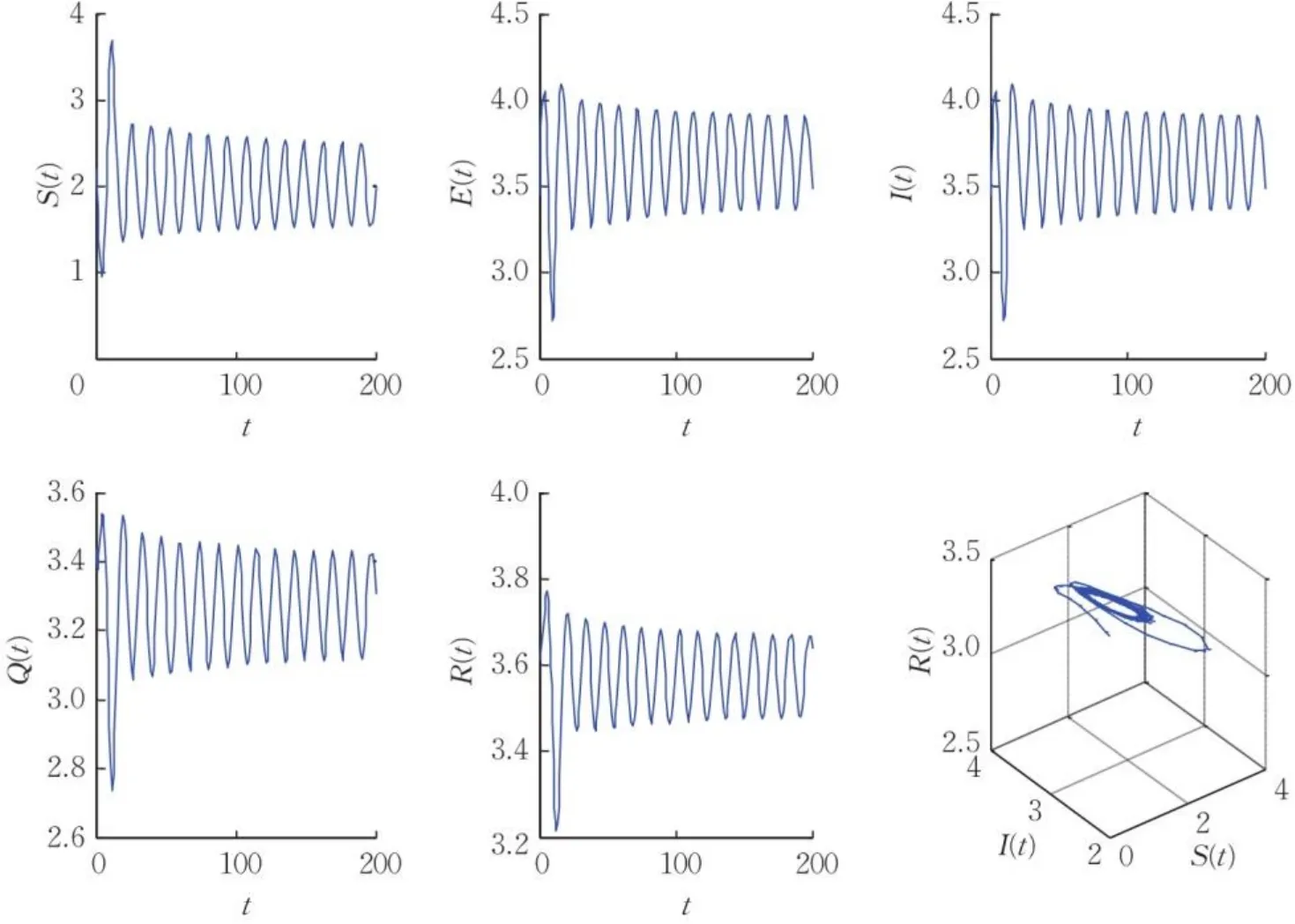
图2 当时，示例模型产生Hopf分岔Fig.2 When ， the example model appears Hopf bifurcation

7 结论

基于文献［19］，建立了考虑潜伏状态和隔离状态的具有混合隔离策略的非线性计算机病毒传播模型。不仅考虑了潜伏期时滞和由杀毒软件导致的临时免疫期时滞，而且考虑了不同状态计算机因受感染程度不同，其隔离率不同的情况。相比文献［19］，本文模型引入了更多现实因素，更贴合实际。在讨论模型的局部渐近稳定时，将不同的时滞组合作为分岔参数，进行了较为全面的研究。

研究发现，在一定条件下，当时滞小于临界值时，采取切实可行的措施可很好地控制计算机病毒；当时滞超过临界值时，计算机病毒将失去控制。因此，在恰当的时机采取措施，对控制计算机病毒十分必要。

利用中心流形定理和规范型理论分析了Hopf分岔方向和周期解的稳定性。为验证理论分析的正确性，用符合假设条件的示例进行数值模拟，确保了研究结果的有效性。在今后的工作中，将进一步探讨模型的全局稳定性。

［1］中国互联网络信息发展中心. 第49次中国互联网络发展状况统计报告［EB/OL］.（2022-02-25）. http：//www.cnnic.cn/hlwfzyj/hlwxzbg/hlwtjbg/202202/t20220225_71727.htm

China Internet Network Information Center. The 49th Statistical Report on Chinaapos;s Internet Development［EB/OL］. （2021-02-25）.http：//www.cnnic.cn/hlwfzyj/hlwxzbg/hlwtjbg/202202/t20220225_71727.htm

［2］国家信息中心，北京瑞星网安技术股份有限公司. 2021年中国网络安全报告［EB/OL］. （2022-02-23）. http：//it.rising.com.cn/dongtai/19859.html

The State Information Center，Beijing Rising Network Security Technology Co.，Ltd. 2021 China Cyber Security Report［EB/OL］. （2022-02-23）.http：//it.rising.com.cn/dongtai/19859.html

［3］KEPHART J O， WHITE S R. Directed-graph epidemiological models of computer viruses［C］// Proceedings of the 1991 IEEE Computer Society Symposium on Research in Security and Privacy. Oakland：IEEE， 1991：343-359. DOI：10.1109/RISP.1991.130801

［4］PASTOR-SATORRAS R， VESPIGNANI A. Epidemic dynamics and endemic states in complex networks［J］. Physical Review E， 2001， 63（6）：0661171-0661178. DOI：10.48550/arXiv.cond-mat/0102028

［5］姚丽丽，马英红，李慧嘉. 一种带隔离机制的SIS模型研究［J］. 计算机安全，2010， 2（2）：91-92. DOI：10.3969/j.issn.1671-0428.2010.02.033

YAO L L， MA Y H，LI H J. The study of SIS model with time isolation mechanism［J］. Network and Computer Security， 2010，2（2）： 91-92. DOI：10.3969/j.issn.1671-0428.2010.02.033

［6］JOHN C W， DAVID J M. Modeling computer virus prevalence with a susceptible-infected-susceptible model with reintroduction［J］. Computational Statistics amp; Data Analysis， 2004，45（1）： 3-23. DOI：10.1016/S0167-9473（03）00113-0

［7］ZHU L H， GUAN G， LI Y M. Nonlinear dynamical analysis and control strategies of a network-based SIS epidemic model with time delay［J］. Applied Mathematical Modelling， 2019，70（18）：512-531. DOI：10.1016/j.apm.2019.01.037

［8］MUROYA Y， ENATSU Y，LI H X. Global stability of a delayed SIRS computer virus propagation model［J］. International Journal of Computer Mathematics， 2014，91（3）：347-367. DOI：10.1016/j.apm.2019.01.037

［9］ZHANG X X， LI C D，HUANG T W. Impact of impulsive detoxication on the spread of computer virus［J］. Advances in Difference Equations， 2016，2016（1）： 1-18. DOI：10.1186/s13662-016-0944-x

［10］陈实，肖敏，周颖，等. 一类具有饱和发生率的时滞恶意病毒传播模型的Hopf分岔［J］. 南京理工大学学报（自然科学版），2021， 45（3）：320-325，331. DOI：10.14177/j.cnki.32-1397n.2021.45.03.009

CHEN S， XIAO M，ZHOU Y， et al. Hopf bifurcation of malicious virus spreading model with time delays and saturated incidence rate［J］. Journal of Nanjing University of Science and Technology，2021， 45（3）：320-325，331. DOI：10.14177/j.cnki.32-1397n.2021.45.03.009

［11］王刚，冯云，马润年. 操作系统病毒时滞传播模型及抑制策略设计［J］. 西安交通大学学报， 2021，55（3）： 11-19. DOI：10.7652/xjtuxb202103002

WANG G， FENG Y，MA R N. Time-delay propagation model and suppression strategy of operating system virus［J］. Journal of Xiapos;an Jiaotong University，2021， 55（3）：11-19. DOI：：10.7652/xjtuxb202103002

［12］YUAN H， CHEN G Q. Network virus-epidemic model with the point-to-group information propagation［J］. Applied Mathematics and Computation， 2008，206 （1）： 357-367. DOI：10. 1016/j.amc.2008.09.025

［13］LI J Q， YANG Y L，ZHOU Y C. Global stability of an epidemic model with latent stage and vaccination［J］. Nonlinear Analysis：Real World Applications， 2010，12（4）： 2163-2173. DOI：10.1016/j.nonrwa.2010.12.030

［14］FENG L P， HAN R F，WANG H B， et al. A virus propagation model and optimal control strategy in the point-to-group network to information security investment［J］. Complexity，2021， 2021（6）：1-7. DOI：10.1155/2021/6612451

［15］尹礼寿，梁娟. 一类计算机病毒SEIR模型稳定性分析［J］. 生物数学学报，2017， 32（3）：403-407.

YIN L S， LIANG J. The stability analysis of one kind of computer virus SEIR model［J］. Journal of Biomathematics， 2017，32（3）： 403-407.

［16］LIU Q M， LI H. Global dynamics analysis of an SEIR epidemic model with discrete delay on complex network［J］. Physica A：Statistical Mechanics and Its Applications， 2019，524（6）： 289-296. DOI：10.1016/j.physa.2019.04.258

［17］AMADOR J， ARTALEJO J R. Stochastic modeling of computer virus spreading with warning signals［J］. Journal of the Franklin Institute， 2013，350（5）： 1112-1138. DOI：10.1016/j.jfranklin.2013.02.008

［18］YANG L X， DRAIEF M，YANG X F. Heterogeneous virus propagation in networks：A theoretical study［J］. Mathematical Methods in the Applied Sciences， 2017，40（5）： 1396-1413. DOI：10.1002/mma.4061

［19］MADHUSUDANAN V， GREETHA R. Dynamics of epidemic computer virus spreading model with delays［J］. Wireless Personal Communications， 2020，115（5）： 2017-2061. DOI：10.1007/s11277-020-07668-6

［20］DRIESSCHE P， WATMOUGH J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission［J］. Mathematical Biosciences， 2002，180（1/2）：29-48. DOI：10.1016/S0025-5564（02）00108-6

［21］HASSARD B D， KAZARINOFF N D，WAN Y H. Theory and Applications of Hopf Bifurcation［M］. Cambridge/New York： Cambridge University Press，1981.

［22］李畅. 混合隔离策略和时滞因素对计算机病毒在网络中传播的影响研究［D］. 重庆：西南大学， 2016.

LI C. The Impact of Hybrid Quarantine Strategies and Delay Factor on Viral Prevalence in Computer Networks［D］. Chongqing： Southwest University，2016.

［23］蔡秀梅. 计算机病毒传播模型的研究与稳定性分析［D］. 重庆：重庆理工大学， 2019.

CAI X M. Research and Stability Analysis of Computer Virus Propagation Model［D］. Chongqing： Chongqing University of Technology，2019.

［24］GAO Q W， ZHUANG J. Stability analysis and control strategies for worm attack in mobile networks via a VEIQS propagation model［J］. Applied Mathematics and Computation， 2020，368（1）： 124584. DOI：10.1016/j.amc.2019.124584

Hopf bifurcation of nonlinear computer virus propagation model with hybrid quarantine strategy

YANG Fangfang, ZHANG Zizhen

（School of Management Science and Engineering，Anhui University of Finance and Economics，Bengbu233030，Anhui Province，China）

The establishment of a nonlinear computer virus propagation model with hybrid isolation strategy is helpful for understanding the propagation law of computer virus in the network. This paper proposes a new model which considers latency delay and temporary immune delay. Firstly, the basic regeneration number of the model is calculated. Then, the local asymptotic stability of the model is studied by taking the combination of different time delays as bifurcation parameters. Afterwards, the direction of Hopf bifurcation and the stability of periodic solution are calculated by using the central manifold theorem and normal form theory. The theoretical analysis is verified by numerical simulation. The research results can provide a theoretical basis for the treatment of computer virus in the future.

hybrid quarantine strategy; time delay; Hopf bifurcation; numerical simulation

TP 309

A

1008⁃9497（2022）05⁃570⁃10

2021⁃03⁃15.

国家自然科学基金资助项目（12061033）.

杨芳芳（1997—），ORCID：https：//orcid.org/0000-0002-5375-7133，女，硕士研究生，主要从事动力系统稳定性、分岔研究.

通信作者，ORCID：https：//orcid.org/0000-0002-2879-4434，E-mail：zzzhaida@163.com.

10.3785/j.issn.1008-9497.2022.05.008