一类具变指数的非线性椭圆方程在加权Sobolev空间中熵解的存在性
2022-09-17代丽丽
代丽丽
(通化师范学院 数学学院, 吉林 通化 134002)
一类具变指数的非线性椭圆方程在加权Sobolev空间中熵解的存在性
代丽丽
(通化师范学院 数学学院, 吉林 通化 134002)
运用截断函数方法以及变指数在加权Sobolev空间中的嵌入关系,通过选取适当的检验函数,证明了一类非线性椭圆方程熵解的存在性。
非线性椭圆方程;截断函数;加权Sobolev空间;权函数
0 引言
在加权Sobolev空间中,考虑一般情形的非线性椭圆方程
(H1)为Carathéodory的向量值函数,对几乎处处的,所有的,满足
(H2)→R为Carathéodory函数,且对几乎处处的和任意的,所有的,满足
AHAROUCH等[1]研究了在常指数情形下,当,且时,式(1)在Orlicz空间解的存在性结果。在变指数情形下,AZROUL等[2]研究了椭圆方程
并得到熵解的存在性结果。ZHANG等[3]在,,,且的情形下,证明了重整化解和熵解的存在性。BOCCARDO等[4]运用截断方法,证明了当为常函数,,时,式(1)在Sobolev空间中重整化解的存在性和正则性。此后,BOCCARDO等[5]继续研究带有非线性导数项的非线性椭圆方程,并证明了其存在解。
以上研究均在不加权的Sobolev空间进行。本文将在文献[2-3]等的基础上,引入权函数,扩展为加权变指数的Sobolev空间,并在此框架下,研究式(1)解的存在性。首先,带变指数的偏微分方程模型相较常指数优势显著,其可更精确地描述扩散过程,当不是常函数时,研究相关加权的文献较少,需特别关注空间的性质及嵌入。其次,权函数的引入增加了研究的难度,尤为困难的是空间的嵌入。最后,函数无增加任何条件,即使作为一个分布,此项在方程中也可能无意义,且右端项可积性不高。因无法得到式(1)的弱能量解,所以考虑其熵解。本文主要借助截断函数方法对逼近方程做估计,运用加权变指数在Sobolev空间中的嵌入关系,选取合适的检验函数,令强收敛,并通过取极限,得到式(1)的熵解。
1 相关知识
给出加权变指数在Sobolev空间的相关知识[6]。
赋予范数
(iii)常用关系。如果记
那么
(v)加权变指数在Sobolev空间中的连续嵌入定理。设满足-连续性条件,若且,则有连续嵌入
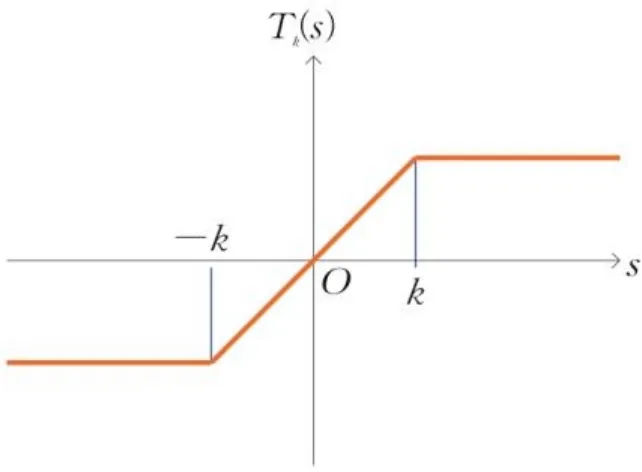
图1 Tk(s)Fig.1 Tk(s)
引理1设和是2个非负实数,
引理2对任意的和,有
引理3假设和()成立,设在中弱收敛于且满足
2 熵解的存在性
定义1若,且对任意的,均有
定理1若成立,,则式(1)至少存在1个熵解。
证明 分5步完成证明过程[9-11]。
第1步 逼近问题及先验估计。
建立关于式(1)的逼近方程
由文献[12-13]的伪单调算子理论,可知式(10)至少存在1个弱解,即对任意的有
具体来看,一方面要在保证产品安全有效、质量可控的前提下,改革审评审批机制,简化特殊食品变更注册和延续注册程序;另一方面,监管部门要严格执行特殊食品生产经营许可相关规定,督促企业按照良好生产规范要求,建立生产质量管理体系。
由式(3)、式(5)、式(19)及Young不等式,式(12)可整理为
即
由加权变指数在Sobolev空间的嵌入定理,有
其中,
第2步在上几乎处处收敛。即证明是一个依测度收敛的柯西序列。
即
第3步在中强收敛。
于是可将式(18)整理为
方便起见,写为
类似地,有
于是,
联合式(14)和式(22),有
综上,由式(23)和式(27),可将式(19)左端整理为
由引理1,取a=1,b=,结合式(28)~式(30),且当时,对式(19)取极限,有
事实上,对于右端第1项,应用Lebesgue控制收敛定理便可得到结果。
对于右端第2项,不妨设
用证明式(19)类似的方法,可得
由式(3)、式(5)及Young不等式,有
即
由引理3,有
第4步 非线性项在中强收敛。
由符号条件式(5),可知
用证明式(19)类似的方法,可得
由式(3)和Young不等式,可得
移项后去掉非负项,可得
于是,有
由式(35)和式(37),可知当m充分大时,至少存在1个,使得当时,有
第5步 取极限。
由Fatou引理,有
且
于是有
定理1得证。
[1]AHAROUCH L,BENNOUNA J,TOUZANI A.Existence of renormalized solution of some elliptic problems in Orlicz space[J]. Revista Matematica Complutense, 2009,22:91-110.
[2]AZROUL E, BENBOUBKER M B,RHOUDAF M. On somep(x)-quasilinear problem with right-hand side measure[J]. Mathematics and Computers in Simulation, 2014,102: 117-130. DOI:10.1016/j.matcom.2013.09.009
[3]ZHANG C, ZHOU S L. Entropy and renormalized solutions for thep(x)-Laplacian equation with measure data[J]. Bulletin of the Australian Mathematical Society, 2010,82(3): 459-479. DOI:10.1017/S0004972710000432
[4]BOCCARDO L, GIACHETTI D,DIAZ J 1, et al. Existence and regularity of renormalized solutions for some elliptic problems involving derivatives of nonlinear terms[J]. Journal of Differential Equations, 1993,106(2): 215-237. DOI:10.1006/jdeq.1993.1106
[5]BOCCARDO L,CROCE G,ORSINA L. Existence of solutions for some noncoercive elliptic problems involving derivatives of nonlinear terms[J]. Differential Equations and Applications, 2012,4(1): 3-9. DOI:10.7153/dea-04-02
[6]GOLDSHTEIN V, UKHLOV A. Weighted Sobolev spaces and embedding theorems[J]. Transactions of the American Mathematical Society, 2009,361(7): 3829-3850. DOI:10.48550/arXiv.math/0703725
[7]BLANCHARD D. Truncations and monotonicity methods for parabolic equations[J]. Nonlinear Analysis: Theory,Methods amp; Applications, 1993,21(10):725-743. DOI:10.1016/0362-546X(93)90120-H
[8]BLANCHARD D, MURAT F,REDWANE H. Existence and uniqueness of a renormalized solution for a fairly general class of nonlinear parabolic problems[J]. Journal of Differential Equations, 2001,177(2): 331-374. DOI:10.1006/jdeq.2000. 4013
[9]BENBOUBKER M B, CHRAYTEH H,MOUMNI M E, et al. Entropy and renormalized solutions for nonlinear elliptic problem involving variable exponent and measure data[J]. Acta Mathematica Sinica,2015, 31(1):151-169. DOI:10.1007/s10114-015-3555-7
[10]DAl L L, GAO W J,LI Z Q. Existence of solutions for degenerate elliptic problems in weighted Sobolev space[J]. Journal of Function Spaces, 2015,2015: 1-9. DOI:10.1155/2015/265127
[11]代丽丽. 一类具退化强制的椭圆方程熵解的存在性[J]. 华东师范大学学报(自然科学版),2019(4): 52-61. DOI:10.3969/j.issn.1000-5641.2019.04.006
DAI L L. Existence of entropy solutions for an elliptic equation with degenerate coercivity[J]. Journal of East China Normal University(Natural Science), 2019(4):52-61. DOI:10.3969/j.issn.1000-5641. 2019.04.006
[12]LIONS J L. Quelques Méthodes de Résolution des Problemes Aux Limites Nonlinéaires[M]. Paris:Dunod, 1969.
[13]SCHWARTZ J T. Nonlinear Functional Analysis[M]. Boca Raton: CRC Press,1969.
The existence of entropy solutions for the nonlinear elliptic problems with variable exponents in weighted Sobolev space
DAI Lili
(Institute of Mathematics,Tonghua Normal University,Tonghua134002,Jilin Province,China)
In this paper, we utilize truncation method and some embedding of weighted Sobolev space with variable exponent to investigate the existence of entropy solutions for the nonlinear elliptic problems.
the nonlinear elliptic equation; truncation function; weighted Sobolev space; weighted functions
O 175.2
A
1008⁃9497(2022)05⁃540⁃09
2020⁃12⁃02.
吉林省教育厅科学研究项目(JJKH20210537KJ).
代丽丽(1982—),ORCID:https://orcid.org/0000-0002-6376-6949,女,博士,副教授,主要从事偏微分方程及其应用研究,E-mail:drx820115@126.com.
10.3785/j.issn.1008-9497.2022.05.004
