基于内点罚函数的全双工认知无线电网络优化

姜海滨，余志勇，杨 剑，韩宇宸

（火箭军工程大学，陕西 西安 700025）

在半双工认知无线电网络（Half⁃Duplex Cognitive Radio Network，HD⁃CRN）中，次 级 用 户（Secondary Users，SU）将连续的感知时隙划分为两段，在前段SU主要进行频谱感知，即检测主用户（Primary Users，PU）是否在使用授权频段；后段SU主要进行次级网络的数据传输。这种方式会带来两个问题：一是SU牺牲了一段时间用于频谱感知，用于数据传输的时间减少；二是SU在进行数据传输时无法进行频谱的感知，如果此时PU加入网络，势必造成冲突，影响PU通信。近年来，全双工（Full⁃Duplex，FD）通信技术越来越受到人们的关注，因为在同一个信道中可以进行双向通信，所以全双工技术可以将频谱的利用率提高1倍。但是，全双工认知通信的自干扰问题限制了它的广泛应用，因而自干扰消除技术成为当前全双工认知通信研究的热点之一。自干扰消除技术主要有无源消除、有源消除和天线极化分集等。

将全双工技术引入到认知无线电网络中，从而得到全双工认知无线电网络（Full⁃Duplex Cognitive RadioNetwork，FD⁃CRN）。在FD⁃CRN中，SU在进行频谱感知的同时还可以进行数据的传输，提高了认知无线电网络的性能。目前的研究工作主要有使用双阈值能量检测、优化频谱资源的分配、改变感知模式等方法来提高FD⁃CRN的单位带宽吞吐量，但对于如何通过优化频谱检测阈值来提高传输网络吞吐量的问题则鲜有公开文献涉及。本文基内点罚函数优化理论，提出一种基于优化检测阈值来提升系统单位带宽吞吐量的技术，可以达到提高频谱利用率的效果。

1 系统模型

根据全双工认知无线电网络，建立如图1所示的全双工认知无线电网络模型。

图1 全双工认知无线电网络模型

图1所示为FD⁃CRN的模型。假设PU为频谱的授权用户，可以自由使用授权频段，且无线电网络中只有一个感知用户SU，SU的数据传输对象只有一个SU。在时隙化的感知模型中，PU对数据的使用建模为在感知的每个时隙接入或者退出的随机过程。感知用户SU配备接收天线Ant和发射天线Ant两个天线。其中，Ant为感知天线，负责频谱的感知；Ant为数据传输天线，负责次级传输网络的数据传输。SU根据Ant感知的结果，来判断Ant是否进行数据传输。

2 单位带宽吞吐量优化

为在全双工认知无线电网络中提高频谱的利用率，本文建立全双工马尔科夫转移模型，以此为基础定义单位带宽吞吐量的概念，并通过优化频谱感知中能量检测的阈值来提升系统单位带宽吞吐量。

2.1 能量检测

根据信号平均功率，构造检测统计量，表示为：

式中：N=Tf为采样点个数，f为采样频率，为采样时隙；()为检测信号。由于()为独立同分布，根据中心极限定理，的概率密度函数近似为高斯分布。

如图2所示的次级用户感知传输模型中，Ant接收到的信号可能处于四种状态：当SU没有进行数据传输时，PU使用或者不使用授权频段；当SU进行数据的传输时，PU使用或者不使用授权频段。接收信号()可表示为：

图2 次级用户感知传输模型

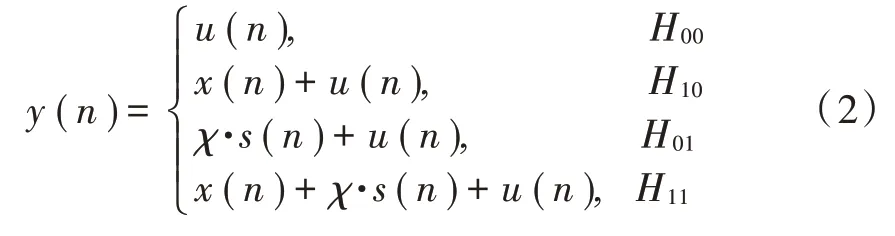
表1 高斯分布模型

在能量检测算法中，要预先设定检测阈值。而在全双工网络中，由于SU&Ant可能传输数据，因此用表示SU未传输数据时的能量检测阈值，在假设条件、下，P表示假设条件下的虚警概率，当PU未使用授权频段时SU误判其使用频段，P表示假设条件下的漏检概率，而当PU使用授权频段时SU误判其未使用频段；用表示SU传输数据时的能量检测阈值，即在假设条件，下，P表示假设条件下的虚警概率，P表示假设条件下的漏检概率。综上可得：

其中

同理，可得:

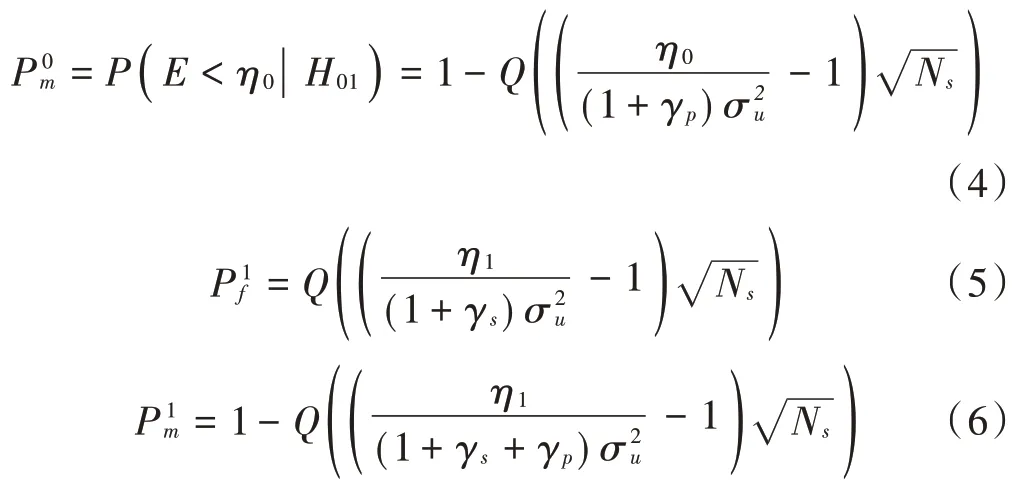
2.2 全双工状态转移模型

由于PU对授权频段的接入和退出过程是具有无后效性的随机过程，因此，可以将4种状态之间的变化建模为2个离散时间马尔科夫链，其转移概率如图3所示。在建立模型时，由于PU状态的变化相对于感知时隙来说非常缓慢，且总的来说，PU改变状态的时隙占比不大，因此，忽略PU改变其状态的时隙，即假设在一个感知时隙中，PU不改变其状态。

图3 SU状态转移图

假设p(,=0,1)表示系统处于每个状态的概率，根据SU的状态转移的马尔科夫模型以及一步转移概率，可得：

假设p表示全双工系统的漏检概率，p表示全双工系统的虚警概率，可得：

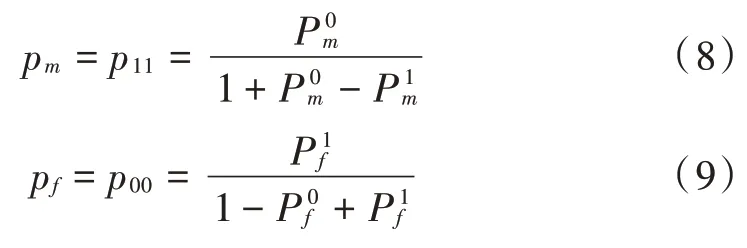
2.3 基于内点罚函数法的单位带宽吞吐量优化

为了衡量次级传输网络的性能，根据系统误码率和香农公式，定义指标为单位带宽吞吐量（Average Throughput），即频谱利用率的表达式为：

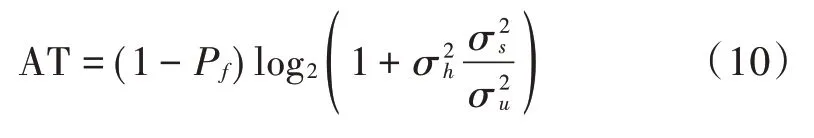
式中，为SU到SU的瑞利信道方差。

为了保护主网络不受干扰，根据IEEE 802.22无线区域网络标准，在认知无线电网络中，要求次级网络至少有90%以上的检测概率，即要求p≤0.1，在这里假设p≤p。同时，将和限制在p以下，在那么单位带宽容量最大化问题就可以转化为一个非线性约束下的优化问题，即：

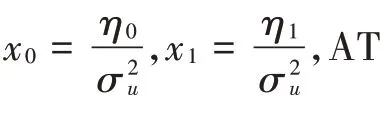
然后，采用内点罚函数的方法将约束优化问题转化为无约束极值问题。通过一系列罚因子{c}，求解罚函数的极小点，从而逼近原约束问题的最优解。算法的流程如下：

1）给定初始点，罚因子>0，缩小系数>1，以及精度>0，置=1。

2）构造增广目标函数：

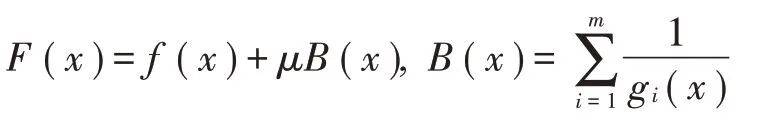
3）用牛顿法求解无约束非线性规划，以x为初始点求解min()，设最优解为x，若(x)<，则停止迭代输出x；否则令=，=+1，转步骤2）。

3 仿真分析

通过仿真验证优化后系统单位带宽吞吐量的提升，首先验证优化后的检测阈值。在仿真中设置的参数如表2所示。

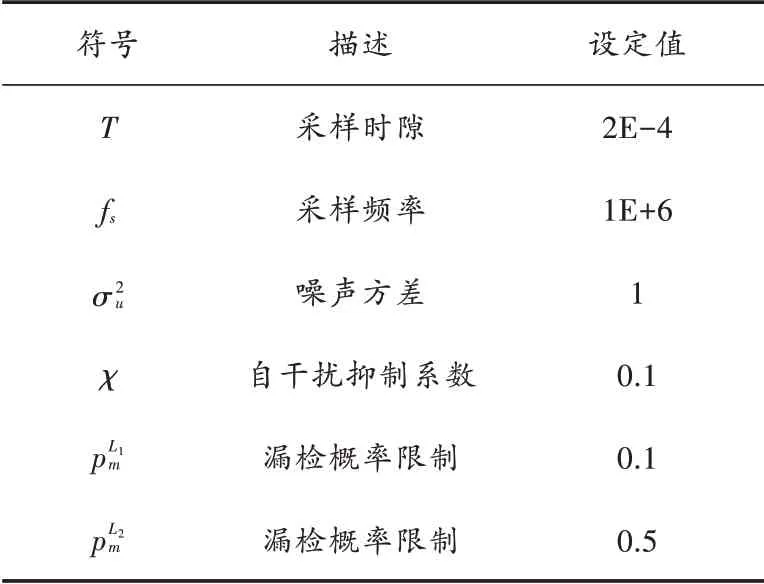
表2 系统参数设置

在不同的 σ和 σ下，使用内点罚函数法得到AT取极大值时最优检测阈值，，如图4所示。

图4 最优检测阈值变化

从图4可以看出：，的值随着感知用户SU信噪比的变化而变化，信噪比越大，感知用户的检测阈值越大；而随着干噪比的变化，的变化不明显，但是在 σ的大于20 dB时，的值随着 σ的增大而显著增大。

文献[11]在没有优化检测阈值的情形下，得到了SU单位带宽吞吐量，在本文使用优化的检测阈值来提高系统的单位带宽吞吐量。当SU相对传输功率为0~30 dB时，在图5显示了单位带宽吞吐量AT与SU的相对传输功率（ σ）的关系。

图5 SU传输功率和吞吐量的关系

如图5所示，SU的感知信噪比 σ=-5 dB，自干扰抑制系数分别为0.1，0.15，0.2时，可以得到，当SU处于高传输功率时，本文提出的优化算法优化后的值有明显提升。例如，当 σ=20 dB，=0.1时，本文优化后的AT为8.4（b/s）/Hz，在文献[11]中则为5.9（b/s）/Hz，AT的值提升了42.4%。

图中虚线的值为AT值的理论最大值，即当p=0时，系统单位带宽吞吐量的值的极限值。从图5中可以看出，当SU的传输功率比较小时，本文所提优化算法和文献[11]中的AT值均接近于极限值。因为此时系统的自干扰比较小，故虚警概率比较小，从而对系统的感知结果影响不大。但是随着传输功率的不断提升，自干扰也越来大，增加了系统的虚警概率，系统的AT值与极限值差距越来越大。

从图5中也可以看到，随着传输功率的增大，AT的值在上升到一定的极值后，单位带宽吞吐量的值将随着功率的增大而减小，这是因为功率的增大导致系统的自干扰不断增大，系统的虚警概率不断增大，对系统的影响也越来越大。

当 σ=10 dB，自干扰抑制系数分别为0.1，0.15，0.2时，SNR与单位带宽吞吐量关系如图6所示。当SNR较低时（小于-5 dB）时，由于本文算法优化了检测阈值，因此吞吐量比文献[11]高出40%~65%。例如SNR=-10 dB，=0.1时，优化后的AT值为3.2（b/s）/Hz，在文献[11]中则为5.2（b/s）/Hz，AT值提升了62.5%。但是，当处于高信噪比时（大于-5 dB）时，算法的优化效果并不明显，因为吞吐量均达到了上限。另外，当信噪比相同时，值越小，次级传输网络单位带宽的值越大，这是因为自干扰会影响系统的检测概率。

图6 SU信噪比和吞吐量的关系

4 结 语

本文提出一种全双工的认知无线电网络系统，由于系统具有自干扰抑制能力，认知用户在感知授权用户频段的同时，还可以进行数据的传输，从而能够有效提升系统的频谱利用率，即次级网络的单位带宽吞吐量。为此，首先建立状态转移模型，得到系统的虚警概率P和检测概率P；然后通过内点罚函数法，得到最优带宽吞吐量下的检测阈值，显著提升了系统单位带宽吞吐量。本文只研究了一个感知用户和一个数据传输对象的系统，忽略了在SU感知时隙中PU状态的改变，在下一步还需要针对多感知用户和多传输对象系统的非时隙状态转移问题进行深入探讨。