基于量子粒子群的定模动辊装备系统动力学优化
2022-09-17李傲然李强
李傲然,李强
(北方工业大学机械与材料工程学院,北京 100144)
0 前言
变截面辊弯成形构件可以根据载荷情况确定截面几何形状,实现等强度设计,有效减少零件质量。对于超高强钢等传统冲压工艺难以成形的材料,变截面辊弯渐进成形技术有着独有的优势,可以有效减少缺陷,实现复杂构件成形。变截面辊弯成形的工作原理:以多个道次成组运行,每一个道次承担预先计算好的成形量,通过各个道次的成形累加,最终实现目标零件的加工。
在汽车、高速列车、航空及航天工业中,如何保证产品强度、刚度以及轻量化制造是追求目标。为适应当代绿色制造要求,提高辊弯成形件的质量,对辊弯成形机电设备性能提出了更高要求,如何实现变截面辊弯成形过程中系统动力学性能优化是装备研制需要解决的问题。
定模动辊成形机三维模型如图1所示,主要由向运动大机架、5个向运动小机架、模具、实现模具开合的液压气动元件等组成。向驱动电机通过齿轮齿条驱动向运动机架,带动5个道次整体向前运动,轧辊驱动电机驱动轧辊旋转。向电机负责调整轧辊垂向位置。成形板料静止于模具,5个道次轧辊组依次沿模具滚动,每个道次角度分别为30°、50°、70°、84°、84°。

图1 定模动辊成形机三维模型
本文作者基于5个道次的定模动辊成形装备设计的理论问题,以提高装备动力学特性为目标,选择量子粒子群优化算法对其实体装备各零部件的设计参数进行优化,使它在运动过程中获得更小的动态响应加速度。
1 量子粒子群优化算法改进设计
本文作者所研究的最优化问题计算规模庞大,为提高优化效率,探索改进的量子粒子群优化算法成为需要解决的问题。
1.1 基于改变粒子势阱方程的异步寻优策略
标准的量子粒子群优化算法是受粒子群算法的启发,通过仿照量子力学中势场中的粒子从高势能向低势能运动所创造的寻优机制。粒子的极小值可以看为势能最低的点,它的搜索空间可以模拟为量子力学中的势阱,搜索过程可以视为高势能向低势能运动的过程。现有的量子粒子群优化算法采用如下方程进行位置更新:
,(+1)=,±ln[1,()]|()-,()|
(1)
标准量子粒子群优化算法的问题在于随着优化迭代次数的增加,势阱中心的引领作用逐渐减小,粒子信息过于单一,导致求解容易陷入局部最优解、求解效率不高等问题。为此,本文作者提出改进的量子粒子群优化,其改进的主要策略是针对位置更新方程中的势阱长度方程部分进行设计的,具体改进方案如下:
首先,取量子粒子群优化算法中粒子群的平均粒子极值,即在第次迭代中对所有粒子的适应度求和取平均值,其表达方程如下:

(2)
以上述平均粒子极值为界,根据粒子当前适应度对其分类,将适应度()>()的粒子称作劣等粒子,将()<()的粒子称作优等粒子。
对于这两类粒子,分别采用不同的势阱方程进行位置寻优。具体的异步寻优策略:对劣等粒子来说,在寻优过程中应更多地借鉴粒子群中其他粒子的经验来引导飞行,在势阱方程的设计上由粒子平均最优位置avr,()替代当前粒子全局最优位置()来引导飞行,充分分享粒子个体最优位置,()和种群平均最优位置avr,()的位置信息,强化种群当中粒子的协作能力,使更多的粒子信息能够决策劣等粒子的飞行,其位置更新方程设计如下:
,(+1)=,±ln[1,()]·
|avr,()-,()|
(3)
其中:avr()为维的平均最优位置,可表示为
()=[()+()+…+,d()]
(4)
而对于优等粒子来说,应保持自己的飞行经验,按照标准的位置更新模型进行寻优,继续选择以全局最优位置()来引导粒子飞行,在势阱方程的设计上依然采用全局最优位置信息影响个体最优位置,以保证继续向全局最优的势态飞行,其位置更新方程如式(1)所示。
通过以上这种异步寻优策略,可以提高种群中粒子的丰富性,促进种群之间的协作,有利于减轻陷入局部最优解的现象,提高算法寻优的性能。
1.2 基于距离权重系数动态改变粒子收缩扩张系数的寻优策略
在标准的量子粒子群算法中,线性调整收缩扩张系数是控制该系数的主要方式。这种线性的控制方式存在一定的弊端,在迭代前期发现适应度较好的粒子时,由于收缩扩张系数前期较大,导致不能在适应度较好的粒子位置进行细致搜索;而在迭代后期收缩扩张系数较小,导致适应度较差的粒子不能跳出所在的位置,所以存在陷入局部最优解、提前收敛等问题。针对以上问题,本文作者对收缩扩张系数的设计提出改进,以提高算法性能。
本文作者提出距离权重系数的概念,以有效改进收缩扩张系数。距离权重系数的表达式如公式(5)所示:

(5)
式中:为距离权重系数,∈(0,1),且值可以用来表示当前粒子位置与最优粒子位置之间的距离,即权重系数越大,表示其间距越大;相反,权重系数越小,表示其间距越小。
根据提出的距离权重系数的概念设计收缩扩张系数,提出一种基于距离权重系数动态改变收缩扩张系数的寻优策略。设计收缩扩张系数表达式如下:

(6)
式中:为设置的收缩扩张系数的最大值;为设置的收缩扩张系数的最小值。显然,当距离权重系数值越大时,解得的和值也会越大,即当前粒子的位置与最优位置距离较大时,需要加快当前粒子寻找到最优位置的速度;反之,当距离权重系数值越小时,解得的和也会越小,即当前粒子位置与最优位置距离较小时,需要粒子在局部空间内更为精细的寻优,以达到寻找全局最优位置的目标。基于第1.1节中提出的粒子分类策略,对收缩扩张系数的选择策略作如下描述:
对于适应度()>()的劣等粒子,当()<()时,令收缩扩张系数=;否则=。对于适应度()<()的优等粒子,当()<()时,令收缩扩张系数=;否则=。
对于劣等粒子,当()<()时,选择作为收缩扩张系数是因为是一个凹函数,在初期较大且变化速度快,可以更快地收敛到最优位置;对于优等粒子,当()<()时,选择作为收缩扩张系数是因为是一个凸函数,在初期具有较大的值且变化速度缓慢,能够在快速收敛到最优解的基础上还可以维持算法当前的寻优能力,从而取得更好的寻优效果。此外,当()>()时,说明当前粒子所在位置较好,则选取收缩扩张系数的最小值,进行更仔细的局部搜索达到最优解。
1.3 改进量子粒子群算法流程
(1)设置种群数量、粒子维数、最大迭代次数、收缩扩张系数最大值和收缩扩张系数最小值;
(2)初始化粒子群中粒子的位置;
(3)计算步骤(2)中粒子的适应度,进而更新个体最优值与全局最优值的信息;
(4)计算种群中的平均极值,对于适应度()>()的劣等粒子,当()<()时,令收缩扩张系数=,否则=,并且用位置更新方程(3)来更新粒子的位置;对于适应度()<()的优等粒子,当()<()时,令收缩扩张系数=;否则=,并且用位置方程(5)来更新粒子的位置;再次求解全部粒子当前的适应度,然后重置个体最优值和全局最优值的信息;
(5)如果达到所设定的迭代次数,则停止程序;否则重复上述步骤(4)。
1.4 量子粒子群优化算法改进测试
为检验算法改进后的性能,采用如表1所示的3个经典的多峰值测试函数比较算法改进前后的性能,这3个测试函数的理论极小值都是0。

表1 3个经典的测试函数
为保证测试的客观公正、减少实验的偶然性,分别对3个测试函数进行30次实验,且均采用相同的参数设置。其中,共性参数设置:种群数量设为100,迭代次数设为50,收缩扩张系数最大值设为1、最小值为0.5,分别就4维和10维情况下对改进前后的算法进行测试。
根据30次的测试中得到的平均最优值和均方差对算法的性能进行评估,比较结果如表2所示。

表2 3种函数结果比较
3个函数在维数为10的情况下对应的迭代曲线如图2—图4所示。
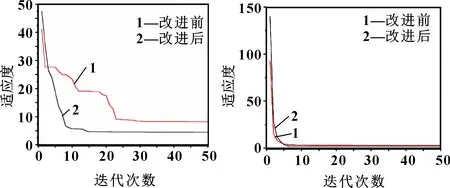
图2 Rastrigrin函数D=10 图3 Griewank函数D=10

图4 Ackley函数D=10时的寻优曲线
由表2和图2—图4可知:在30次测试中,对于3种测试函数改进后的量子粒子群优化算法获得的最优解均更接近于理论值,说明改进后的算法具有更强的寻优性能,且维度越高时体现得越明显;在维数=10时,相较改进前的量子粒子群优化算法,改进后的算法除Ackley函数外,收敛速度均有提升。通过以上测试,可得改进后算法的寻优效率与精度都得到较大改善,所提出的改进策略是有意义的。
2 定模动辊装备优化设计
定模动辊装备系统动力学优化设计可分为:(1)基于能量原理对5个道次的装备系统进行数学建模;(2)通过动力学分析,设计优化的目标函数;(3)选择改进后的量子粒子群优化算法对该机电设备进行优化设计;(4)分析优化结果。
2.1 建立优化模型
文中所研究的定模动辊成形机的机械结构设计已经完成,原始设计参数已经确定,为获得更好的定模动辊装备系统的各零部件的性能参数,可通过建立定模动辊装备系统动力学模型来研究该系统的动力学特征。研究机电耦合相互作用规律,是目前解决大多数机电耦联系统动力学问题的有效途径。定模动辊成形机机电系统动力学方程为


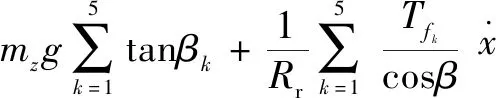
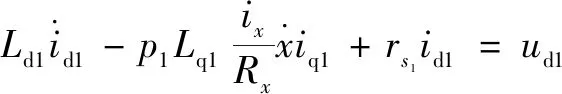




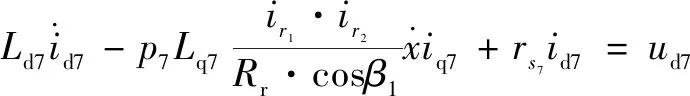

=

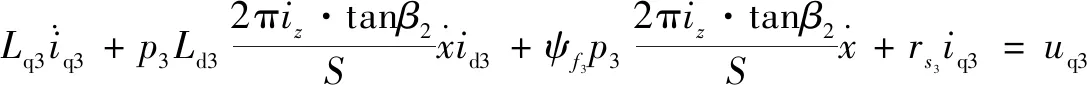


=




=



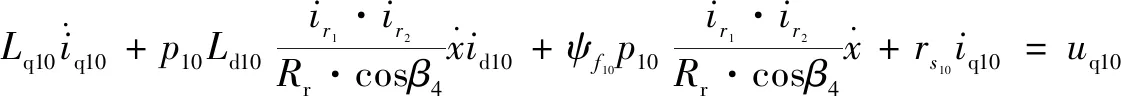
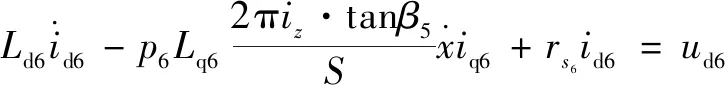

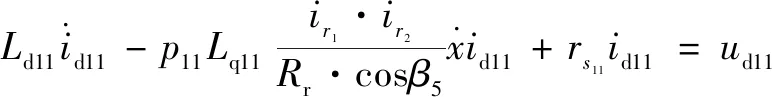

2.2 确定目标函数及优化变量
定模动辊装备系统优化主要是对其各传动链中的各零部件的性能参数进行优化,使各零部件能够合理分配,从而使装备系统获得更好的运动稳定性。因此,选取轧辊、传动齿轮、联轴器的转动惯量,5个道次的机架质量、电机的电感以及相电阻作为优化的设计变量。即优化变量为、、、、、、、、、、…、、、…、、、、…。
以机架向运动动态响应加速度为目标函数,根据定模动辊装备系统的动力学微分方程组,目标函数为
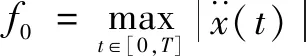
目标函数值通过求解第2.1节中的动力学公式获得。文中采用龙格-库塔法,选取合适的步长,系统初始条件为零,进行方程求解。
选定定模动辊装备系统设计变量的取值范围如表3所示。

表3 设计变量取值范围
2.3 优化算法实现
利用量子粒子群优化算法求解上述优化问题。优化前,对量子粒子群优化算法的参数进行设定,设种群初始值为100,迭代次数为50,收缩扩张系数最大值为1,收缩扩张系数最小值为0.5。设置完成后,用改进的量子粒子群优化算法进行优化求解,其中优化过程中的评价函数值的变化曲线如图5所示。
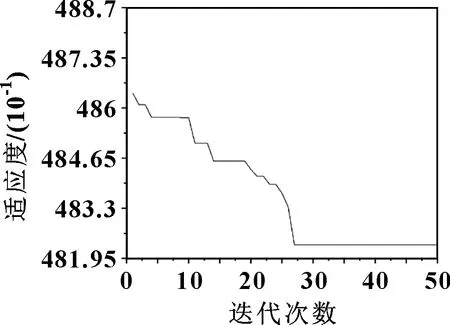
图5 改进量子粒子群优化算法适应度值变化
迭代27次后,适应度不再变化,找到适应度最优解=4.822×10,设计变量优化求解结果如表4所示。

表4 设计变量优化结果
将表4中优化前后的设计变量分别代入第2.1节的微分方程组求解,可得到优化前后的大机架沿向运动的加速度图像,并将两次求解之后大机架沿向移动的加速度进行对比,如图6所示。

图6 优化前后大机架沿x向移动的加速度对比
优化后的大机架沿向移动的加速度较优化前整体减小,其中在5个道次的轧辊电机开始工作时即运动过程中的冲击峰值部分减小较为明显,优化模型整体的峰值在0~2 s内,从0.062 9 m/s降低到0.048 2 m/s。
3 结论
本文作者以定模动辊变高度辊弯成形装备为研究对象,开展机电系统动力学优化研究,实现装备性能优化。通过研究得出如下结论:
(1)基于改变粒子势阱方程的异步寻优策略与基于距离权重系数动态改变粒子收缩扩张系数的寻优策略对量子粒子群算法进行改进,可以提高粒子群算法的寻优效率和速度;
(2)选择改进后的量子粒子群算法对5个道次的定模动辊成形装备进行优化,用改进后的量子粒子群优化算法求解出的各传动链中各零部件的参数对定模装备系统进行设计,减少其向运动过程中的最大加速度,使其在运动过程中冲击峰值明显减少,系统稳定性明显提高,证明应用改进后的量子粒子群优化算法对该机电系统的加速度进行优化是有效的;
(3)由优化结果可知,改进系统设计参数后,装备性能得到改善,研究结果可以为装备研发提供参考。
