基于光滑粒子流体动力学（SPH）方法的环模制粒成型数值模拟方法研究

■孙万峰 王 禹 孙 宇 武 凯

(南京理工大学机械工程学院，江苏南京 210094)

环模制粒工艺及装备以其稳定的生产能力被广 泛应用于生物质能源和饲料工业等领域，目前存在成型能耗高、设备磨损快、制品品质不稳定的问题[1]。为了突破这些技术难题，工程上往往采用试验探索的方法。此外，一旦物料或设备变化，则需要重新试验，效率低、成本高、效果差。而通过数值模拟的方法来代替试验探索则能有效解决这一问题[2]。

目前，成型过程数值模拟相关研究主要结合有限元法和计算流体力学法进行，忽略松散物料颗粒间的相互作用[3]。然而，环模制粒致密成型过程实际上是物料在模辊压力作用下从松散状态变为致密状态的过程，原料颗粒间的相互作用对成型工艺有至关重要的影响[4-5]。此外，环模制粒过程具有非连续循环压制特征，物料被少量多次压入模孔中，并被逐渐挤出。因此，必须考虑颗粒间的相互作用和非连续多次压制条件，从而使仿真与工程实际更吻合。

单个模孔中物料的成型过程是能反映环模制粒工艺特点的最小核心单元。目前对于环模制粒成型机理的研究，多采用将制粒过程简化为单孔挤压等方式进行[6]，试验既能反映物料在模孔内受压并挤出的核心过程[7]，又能降低试验（仿真）成本和难度。

光滑粒子流体动力学（smoothed particle hydrodynamics，SPH）是近20多年来逐步发展起来的一种无网格方法，其主要优点是可以处理基于网格的更大的局部变形[8]。这种方法于1997年引入[9]，最初用于天体物理学中的问题，之后进一步发展将SPH扩展到固体力学[10]。

文章结合LS-DYNA软件利用SPH法对单个模孔中生物质材料非连续多次压制过程进行数值模拟，研究成型过程中压制力的变化情况和物料的流动规律，并将仿真结果与已有研究对比，以期为生物质环模制粒成型过程的数值模拟提供新的方法。

1 原理分析与模型构建

1.1 环模制粒成型原理

环模在电机驱动下带动物料，进而带动压辊同向旋转[11]，如图1所示。一般认为制粒室分为3个部分，分别是供料区、变形压紧区和挤压成型区[12]。物料在环模和压辊的作用下，从供料区经过变形压紧区，最后进入挤压成型区，进而从模孔被挤出，制成致密颗粒。

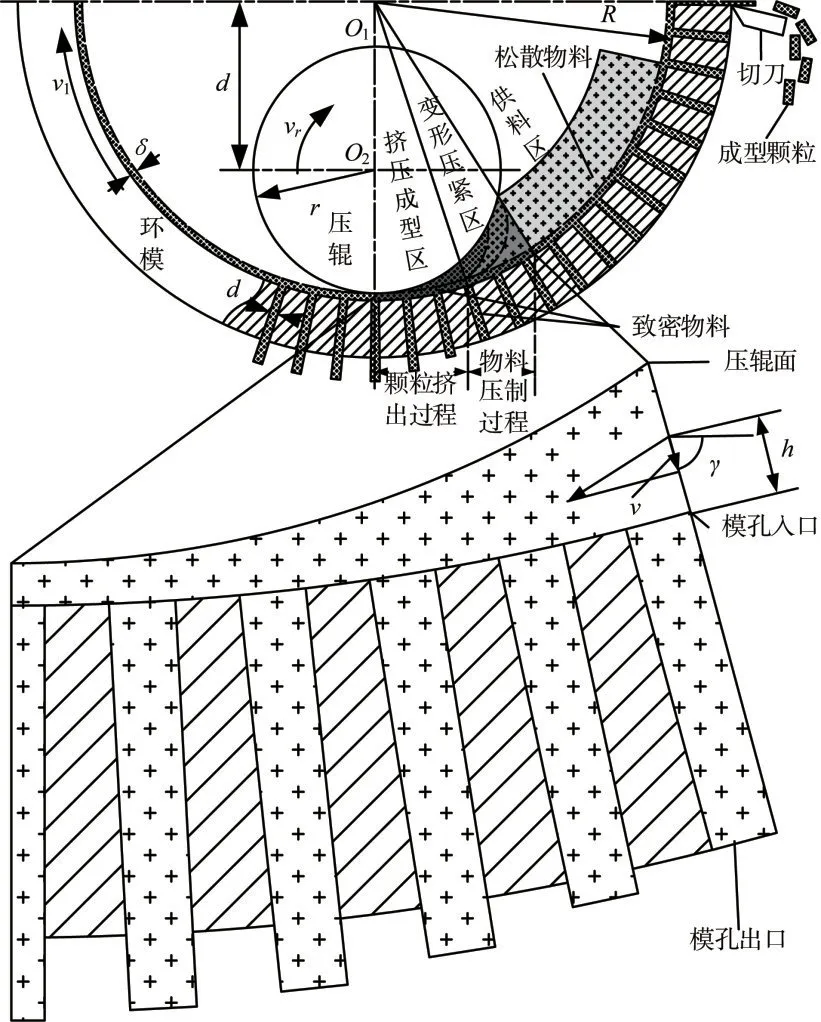
图1 环模制粒成型过程及其放大图

当环模制粒致密成型进入稳定挤压状态时，模孔内压制应力模型如公式（1）[13]。

式中：v——物料被压缩速度（m/s）；

vr——压辊转速（m/s）；

d——模辊中心距（mm）；

r——压辊半径（mm）；

R——环模半径（mm）；

h——物料距环模工作面的距离（mm）；

γ——物料与压辊圆心连线与水平线之间的夹角。

1.2 SPH方法

SPH 的核心是插值，所有宏观变量（如密度、压力、速度等）都通过离散点处的一组值方便地表示为积分插值计算。数值域中点x处的场变量f（x）由公式（3）计算相邻粒子的影响而获得[8]。

N——影响粒子的数量。

上述插值积分的倒数是通过普通推导获得的，不使用有限差分，没有网格，这是SPH 相对于常规数值方法（有限差分或有限元）的主要优势。通过在每个粒子处分配其自己的平滑长度并允许其随时间变化，SPH 模拟可根据当地条件自动进行调整。由于粒子在计算过程中可以相互作用然后分离，因此SPH能够处理非常大的变形[10]。

单孔挤压过程中，物料从横截面大的挤压区进入横截面小的模孔，发生较大的变形，有限元方法会出现网格畸变、计算不收敛等问题，为避免这些问题，采用无网格的SPH方法。

1.3 单孔压制模型的构建

为了研究物料的受力情况，且减少计算量与难度，对环模进行简化，提取出单孔模型[7]。环模制粒机的关键零部件为环模，其工作面如图2所示。环模的工作面是由模孔排列形成的，模孔与模孔之间存在空隙。模孔之间空隙的大小由模孔的横截面及倒角和环模的刚度需求所决定的。环模的开孔率被定义为环模所有模孔的面积与整个环模工作面总面积之间的比值。环模的开孔率通常被设计在30%～40%[7]。

图2 不同模孔排列方式的环模工作面（部分）

由于模孔之间存在空隙，物料在挤压成型区由一块致密的块体被分成若干个小块分别被挤入模孔内。不考虑环模边缘处的模孔，其他模孔如图2 所示，每个模孔周围有4 个或6 个对称分布的模孔，因此，当物料在模孔上方受到挤压时，在模孔径向上，物料的受力是对称的。因而可以沿着图2 中的虚线提取出单个模孔进行研究物料的受力情况，同时将虚线内的区域称为单孔挤压区。

图2中，X表示模孔中心距，为了计算单孔挤压区的大小，借鉴环模开孔率的定义，将单孔挤压区的面积定义公式（5）所示。

式中：S单——单孔挤压区的面积（mm2）；

r——模孔的半径（mm）；

ε——环模开孔率。

2 数值模拟

采用动力学数值模拟软件LS-DYNA实现的SPH方法，因为它能够模拟大变形问题，同时采用重启动或者Dynain文件法可以实现多次挤压过程，可以更好地模拟真实的单孔挤压过程。

2.1 实体模型的建立与网格划分

根据对单孔挤压区的分析，其在径向上是对称受力的，因而本研究中将多边形的单孔挤压区简化为圆形。在数值模拟中，将模型几何体设置为轴对称的3D模型，将模孔尺寸设置成反刍料常用尺寸，具体尺寸如图3所示。

图3 数值模拟的模型及尺寸

在单孔挤压过程中，料筒和模孔仅有其内表面参与物料的压制，因此，将料筒和模孔等几何体设置成壳单元，从而在不影响计算精度的情况下，减少计算量和计算成本。

物料使用SPH粒子进行计算，物料在挤压过程中会发生大变形，使用SPH法可以避免常规的有限元法出现网格畸变等问题。SPH粒子生成的方式很多，文章使用LS-DYNA的前后处理软件LS-PrePost 将已有的Solid单元转换为SPH粒子，具体如图4所示。

图4 网格划分及生成SPH粒子

粒子与模孔之间的接触设置为自动点-面接触（*CONTACT_AUTOMATIC_NODES_TO_SURFACE），可以自动地识别粒子与表面的接触，并防止粒子穿透壳单元，静摩擦系数和动摩擦系数分别设置为0.5和0.3。

2.2 材料设置

环模材料是17CrNiMo，弹性模量E=2.1×1011，泊松比μ=0.25[14]。推板、料筒、模孔等部件使用20 号刚体材料模型（*MAT_RIGID），其中料筒和模孔部分为固定刚体，推板是可以单向移动的刚体。在运行过程中，推板以6 m/s的速度竖直向下压制物料。

物料使用LS-DYNA中基于5号材料弹塑性本构模型（*MAT_SOIL_AND_FORM），结合已有研究中小麦粉的压制曲线来定义模型中的力学参数，小麦粉应力应变曲线如图5所示[15]，对应的压制力位移曲线如图6所示。

图5 小麦粉应力应变曲线

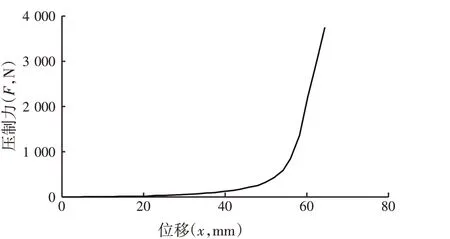
图6 小麦粉单轴压制过程压制力与位移曲线

以环模制粒机K15为例进行仿真，其相关参数为：压辊半径（r）为80 mm，环模半径（R）为350 mm，压辊与环模中心距（d）为92 mm，环模转速（n）为300 r/min。根据公式（2）计算物料的压缩速度，将其简化为匀速运动，压缩速度为6 m/s。因此，将推板下压速度设置为6 m/s，每次下压量为14 mm，留有1 mm 的空隙作为模辊间隙。

2.3 加载过程

在环模制粒机实际运行过程中，环模旋转一周，压辊仅将一小部分原材料压入通道中。因此，物料进给是连续的[16]，所以在数值模拟时，每次压制之前加入一定量的物料。

LS-DYNA的重启动或者Dynain文件法可以记录上一次计算的结果，并完全并入下一次计算中去。因而可以实现多次加料的过程，使用LS-PrePost 生成SPH粒子，第一次压制时生成了4 992个SPH粒子，考虑到环模制粒过程中存在模辊间隙，之后每次压制生成4 224个SPH粒子。第二加载物料如图7所示。

图7 加载物料

3 结果与分析

3.1 物料的流动情况

物料的流动情况可以由物料沿模孔轴向的流速直观地体现出来，如图8 所示。图8 显示了第一次压制和第二压制过程中物料流动速度的剖面图，该图显示了物料由料筒进入模孔中，物料先是向中间流动，然后再进入模孔，这与Nielsen等[6-7]的试验结果一致。Nielsen 等[7]使用红色和蓝色墨水分别对粉料进行着色，使挤压后的颗粒形成不同颜色的分层：在非连续多次挤压试验中，每次挤压前添加固定重量的染色粉料，红色和蓝色粉料交替加入。单孔挤压试验结果如图9所示，通过比较数值模拟的挤压过程流动情况和挤压颗粒剖面图，验证了所提出的SPH模型。

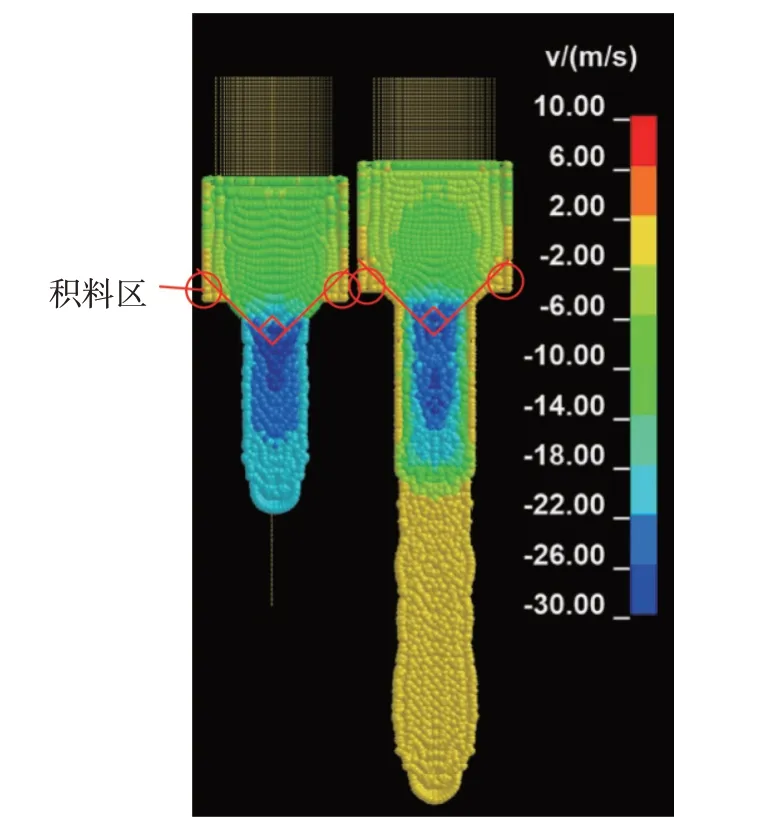
图8 第一次压制和第二次压制过程中的物料流动情况

图9 单孔不连续挤压试验结果[7]

此外，倒角上方的稳定原料的速度等值线在此区域中显示出非常低的速度。表明在料筒底部形成楔形的积料区，积料区与模孔倒角连接到一起，且积料区的角度与模孔倒角的角度基本一致。因此，积料区是模孔倒角的延伸，是物料在压制过程中自动形成的，这与Nielsen等[6-7]的试验结果一致。图9中红色圆圈处显示了在实际单孔挤压过程也会形成楔形积料区，且六次挤压试验结果显示积料区的角度基本一致。六次挤压中使用的物料相同，在倒角不同的模具中进行挤压，表明楔形积料区的角度与倒角的角度没有直接关系。

积料区的形成，有利于物料从料筒进入模孔，在工程应用中，环模模孔的倒角需要根据物料的物理特性进行设计[17]，模拟试验的结果显示，小麦粉进行挤压时宜选用模孔倒角为45°的环模。

3.2 物料的密度分布

在第一次和第二次挤压结束后，物料的密度分布情况如图10 所示。如图10 显示，物料密度沿模孔轴向从入口到出口不断减小。第一次压制后，物料密度的分布情况与流动情况相反，流速大的部分密度反而小。同时，与第一次压制相比，第二次压制后，物料的密度明显增大。第二次压制后，模孔中间处的物料的密度大于边缘处，与物料的流动情况较一致。

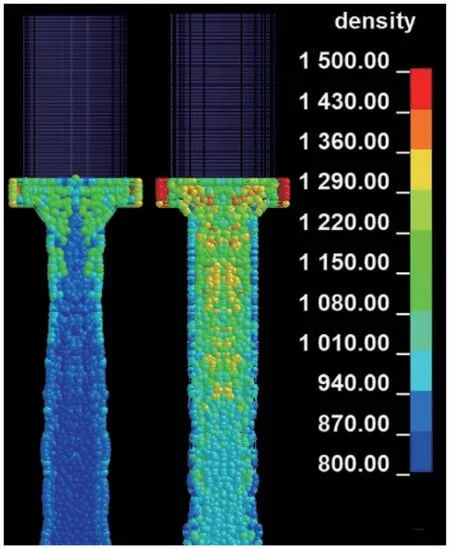
图10 第一次压制和第二次压制结束时物料的密度分布情况

在单孔挤压连续压制过程中，需要背压来启动该过程。背压是由材料在模孔中积聚产生的，这设定了压力（预压力）的要求，以克服模孔内的摩擦[18]。第二次压制与第一次压制之间的差异，其原因可能是第一次压制后模孔入口处物料的密度较大，从而形成较大的背压。

3.3 压制次数与压制力

为了探究压制力与压制次数的关系，进行了多次挤压的单孔挤压过程数值模拟，压制过程中压制力的变化情况如图11 所示。从第二次压制开始，压制力与时间的关系曲线出现两个峰，分析原因：上一次压制完，料筒内物料的密度比模孔内物料的密度大，到达第1 个峰时，新加入的物料的密度达到前一次压制后料筒内物料的密度；推板继续下压，新加入的物料与上次压制后仍停留在料筒内的物料一起被压缩，当推板的压制力等于物料的黏结力及模孔的摩擦力时，出现第2 个峰，随后，料筒内物料被挤入模孔。

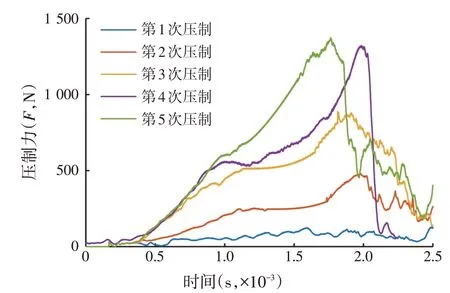
图11 不同挤压次数与压制力

第5次压制时，第1个峰并不明显，且第2个峰峰值与第4 次基本一致，表明第4 次压制完料筒内残留的物料与模孔内物料的密度一致，当新加入的物料与上次压制后料筒内物料的密度一致后，物料的密度不再增加，而是直接被挤出。表明第4 次压制后，进入稳定挤压状态。

4 结论

提出了基于SPH的环模制粒成型数值模拟方法，以小麦粉为对象，结合K15型环模制粒机的结构参数进行了仿真分析。结果显示，小麦粉在压制过程中，物料会在料筒底部形成积料区，其作用与模孔倒角一样可以使物料更好地流动；在进入稳定挤压状态前，模孔入口处物料的密度更大，形成更大的背压，使下一次压制时模孔中间物料的密度更大；当进行4次压制后，单孔挤压进入稳定挤压状态。仿真结果与已有研究结果一致，该方法适用于饲料粉体、秸秆颗粒等松散物料环模制粒过程的数值模拟，对其他领域松散物料模压成型工艺的仿真有指导意义。