基于改进FAHP的数控机床液压系统可靠性分配研究
2022-09-16孙星河于捷林佳颖
孙星河,于捷,2,林佳颖
(1.长春大学机械与车辆工程学院,吉林长春 130022;2.广西梧州学院机械与资源工程学院,广西梧州 543002)
0 前言
数控机床作为我国工业制造发展的“奠基石”,是汇集了多领域专业的机电一体化制造精密设备,其软硬件结构复杂、可实现多种类、高复杂度的加工功能。随着“十四五”发展规划战略的深入实施,国内数控加工正朝着多样化、高速化、高精度化的方向发展。由于数控机床具有技术含量较高、维修和替换成本高昂的特点,所以保证其可靠性是数控机床产品生产的核心竞争力。由于国内大部分具有高精度和高复杂性的零部件均在进口数控机床上制造,这也反映了国内数控机床与国外数控机床相比,在制造产品质量和可靠性上还存在着较大的差距。液压系统是数控机床的核心功能单元,在制造中产品的高性能、高精度也对液压设备的性能、可靠性、安全性和使用寿命等提出了更高的要求。数控机床液压系统的自身结构相对复杂,引起故障的原因同样是复杂多变的。因此,对造成液压系统故障的各类随机因素构建合理的可靠性数学模型,并对数控机床液压系统的设计和配置进行指导。
可靠性分配是可靠性设计的重要环节,科学的配置方法能够使系统设计在消耗最小资源的情况下达到最大的可靠度。可靠性分配过程可以描述为将可靠性需求分配给系统内的各个单元以达到指定的系统可靠性的过程,分配的过程本质是如何在现有资源约束的条件下实现系统可靠性指标的最大化。传统的可靠性分配方法主要有比例分配法、评分分配法、等同分配法、AGREE分配法以及动态规划分配法等。这些方法考虑因素太过单一,不适用于受多因素耦合影响的复杂系统。层次分析法是一种可以考虑系统多种评价因素的数学方法,该方法为可靠性分配提供了全新的思路和指导办法。
针对数控机床液压系统实现如主轴刀具夹紧、工件定位等问题,国内还未有详细的可靠性分配方案。在机械系统可靠性领域内,因系统内各单元具有定量与定性并存,且受到多因素、多层次影响的特性,因此具有较大的不确定性,通过模糊层次分析法来实现合理的可靠性分配。研究以某系列数控机床液压系统为对象,根据液压系统的结构和功能特性,对整个系统进行分类,得到目标层次结构模型,在MATLAB环境下对改进的模糊层次分析法(Fuzzy Analytic Hierarchy Process,FAHP)模型进行程序编写,再通过行业专家评判打分,汇总并导入数据表进行计算,最终得到对象层各元件因素相对于目标层总体的综合权重,为液压系统可靠性分配解决了其中的模糊决策问题,为数控机床液压系统的方案设计和可靠性研究提供了思路。
1 液压系统单元划分与可靠性指标分析
1.1 液压系统单元划分
液压系统是使用压力油作为传递能量的载体来进行传动和控制,不但能够传递动力和运动,而且同时还能够调节机械运动的程序和参量,所以常常被应用在数控设备中。图1所示为液压传动的工作原理。

图1 液压系统传动原理
根据液压系统的结构特性和功能特性,对系统进行结构层次的划分。按照每个结构部件的功能特性,将液压系统划分,如图2所示。

图2 液压系统组成单元及元件
根据液压系统功能特性划分为5个单元,单元内各主要元件为:动力单元-液压泵,执行单元-动力缸(直线运动)和液压电机(回转运动),控制调节单元-压力控制阀、流量控制阀、方向控制阀,辅助单元,工作介质-液压油。
1.2 层次结构模型
对某系列数控机床液压系统进行可靠性分配,要分别确定各元件的权重大小,依据是液压系统在生产中的具体影响因子,主要考虑以下因素:重要程度、工艺复杂度、维修难度、工作环境、成本造价、失效影响。因此,层次结构模型以某系列数控机床液压系统可靠性为目标层,将划分好的6个因素为准则层,组成液压系统的8个部分:液压泵、动力缸、液压电机、压力控制阀、流量控制阀、方向控制阀、辅助单元、液压油为对象层,如图3所示。

图3 可靠性分配层次模型
2 改进的模糊层次分析法应用过程
改进的模糊层次分析法相较于传统的层次分析法,优势在于三标度法属于互补型标度,更适合正常的逻辑思维,且形式较简洁;由优先判断矩阵转化的模糊一致性矩阵满足一致性条件,无须进行一致性检验;提高了解的精度问题及收敛速度问题。其具体步骤如下:
步骤1,建立三标度判断规则,构造互补型模糊判断矩阵。
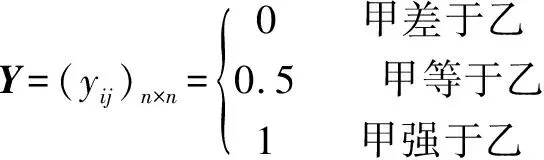
其中:称其为优先判断矩阵;甲表示第行对应的判断因素;乙表示第列对应的判断因素;表示准则层中因素的数量。


(1)
得到模糊一致性判断矩阵:
=()×
(2)
步骤3,计算权重向量。模糊一致性矩阵=()×,每行元素之和(不含自身)为
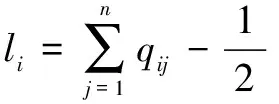
(3)
不包括对角线元素的总和为
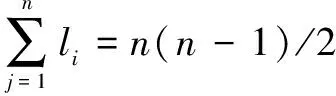
(4)
式中:表示因素相对于上层目标的重要程度。对进行归一化可得到各因素的权重:
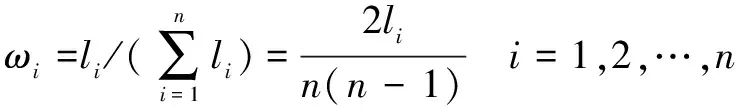
(5)
故权重向量为
=(,,…,)

=(,,…,)=
(6)
步骤5,根据综合权重向量对液压系统整体的可靠度进行分配。在可靠性分析中,对于可靠度的分配通常不是直接进行,而是首先计算整体的允许失效率,再根据对象层A中的各因素综合权重分配各单元所允许的失效率,最后根据进行可靠度分配。和对象层中各单元的权重有如下关系:

(7)
式中:为对象层第个单元应分得的失效率;为对象层第个单元的综合权重。
对象层第个单元应分得的可靠度为
=1-
(8)
3 液压系统可靠性分配
3.1 判断矩阵的建立
通过所构建的模糊层次结构模型和三标度优先判断关系,对准则层的6个因素加以比较,得出各因素对整体系统可靠度分配的影响程度。为了降低研究结论的主观性,综合多位专家的意见,得到各因素的权重关系:重要程度>失效影响>工艺复杂度>工作环境>成本>维修难易度。依据专家意见转换成优先判断矩阵的表现形式,以此进行液压系统可靠度指标的分配。优先关系矩阵见表1。

表1 S-X优先关系矩阵
根据液压系统内各元件在生产中的具体情况,结合专家经验,得出各元件在单一因子影响下的相对关系。
重要程度:液压泵>动力缸=液压电机>压力控制阀>流量控制阀>方向控制阀>辅助单元>液压油。
工艺复杂度:动力缸>液压电机>液压泵>流量控制阀>压力控制阀>方向控制阀>辅助单元>液压油。
维修难度:动力缸>液压泵>液压电机>流量控制阀>压力控制阀>方向控制阀>辅助单元>液压油。
工作环境:液压泵>液压电机>动力缸>液压油>压力控制阀>方向控制阀>流量控制阀>辅助单元。
成本造价:方向控制阀>辅助单元>流量控制阀>液压油>压力控制阀>动力缸>液压电机>液压泵。
失效影响:液压泵>动力缸=液压电机>压力控制阀=流量控制阀>方向控制阀>辅助单元>液压油。
根据改进FAHP方法,循环使用转换关系式,分别得到对象层-相对于准则层6种因素的单独优先关系矩阵,如表2—表7所示。

表2 重要度关系矩阵

表3 工艺复杂度关系矩阵

表4 维修难度关系矩阵

表5 工作环境关系矩阵

表6 成本造价关系矩阵

表7 失效影响程度关系矩阵
3.2 权重确定
在MATLAB环境中编写关于改进FAHP模型程序,主函数如图4所示。

图4 改进FAHP模型主函数
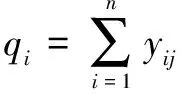
行和:
=55=35=05
=25=15=4.5
模糊一致性矩阵:

将模糊一致性矩阵输入程序内,利用式(3)(4)(5),得出准则层各因素对于目标层的权重:
=(0.250 0,0.183 3,0.083 3,0.150 0,0.116 7,0.216 7)
根据步骤4,依次导入表2—表7的数据,利用MATLAB载入数据重复计算,得到对象层各单元对于准则层单一因素的权重:
=[0.187 5,0.160 7,0.160 7,0.133 9,0.116 1,0.098 2,0.080 4,0.062 5]
=[0.151 8,0.187 5,0.169 6,0.116 1,0.133 9,0.098 2,0.080 4,0.062 5]
=[0.169 6,0.187 5,0.151 8,0.116 1,0.133 9,0.098 2,0.080 4,0.062 5]
=[0.187 5,0.151 8,0.169 6,0.116 1,0.080 4,0.098 2,0.062 5,0.133 9]
=[0.062 5,0.098 2,0.080 4,0.116 1,0.151 8,0.187 5,0.169 6,0.133 9]
=[0.187 5,0.160 7,0.160 7,0.125 0,0.125 0,0.098 2,0.080 4,0.062 5]
将其组成矩阵形式
=[]
通过式(6)计算得到对象层对于目标层的综合权重:
==[0.164 9,0.159 2,0.153 6,0.122 5,0.121 6,0.108 6,0.088 1,0.081 5]
3.3 可靠性分配
对液压系统进行可靠性分配,某系列数控机床的液压系统MTBF指标为1 800 h,可得液压系统失效率要求为=0.000 556,可靠度=0.999 444。根据式(7)得出各元件的故障率:
=0000 049 53=0000 051 30
=0000 053 18=0000 066 67
=0000 067 17=0000 075 21
=0000 092 71=0000 100 21
根据式(8)可得到各元件分配的可靠度为
=(,,,,,,,)
由动力单元、执行单元、控制调节单元、辅助单元、工作介质等组成的液压系统整体的可靠度为
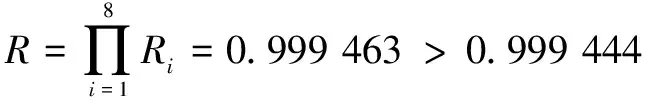
所得结果大于设计指标,满足设计要求。
由上述结果可以看出,以某系列数控机床的液压系统为例,其液压泵、动力缸和液压电机获得了较高的可靠度。在实际生产中,液压泵、动力缸和液压电机易出故障且维修不便。而控制阀和辅助单元则获得了相对较低的可靠度,控制阀和辅助单元的元件属于易更换元件,与实际情况相符。
4 结论
(1)基于改进的FAHP方法,以某系列数控机床液压系统为例,分析了关于液压系统的可靠性分配问题。改进后的FAHP方法针对可靠性指标分配的问题,利用了其中相对重要的模糊因素信息,减少了人脑本身对问题判断的主观因素,充分发挥专家经验对于结果判断的真实作用。
(2)在MATLAB环境中对模型进行编程和计算,从运算结果上看是可行的,与实际情况比较,所得结果与元件现实失效状态相符合。
(3)在研究中仅从各独立单元的主要元件进行了分析,与实际生产中有一定差距,需要进一步从产生故障的各个原因及部位分析,比如运行过程中产生的噪声和振动、气穴和泄漏等故障对整个系统可靠性指标的影响,使得模型更完善,更具有针对性。
