数字伺服系统机械谐振频率偏移现象机制分析及实验研究
2022-09-16张军陈扬洋张杰杨明
张军,陈扬洋,张杰,杨明
(1.广州数控设备有限公司,广东广州 510000;2.哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨 150001)
0 前言
数字伺服控制系统由于能够提升生产效率和方便调试的优点,在数控机床、工业机器人等高精密工业制造和生产场合中有着广泛的运用。伺服系统中电机和负载之间往往通过谐波齿轮、滚轴丝杠、传动皮带等柔性传动装置相连接,以提高设备的兼容性和降低装置的成本。在控制理论中,控制器的高增益往往代表着良好的性能。但相比刚性传动,柔性传动在高增益下更容易出现系统不稳定,从而引发机械谐振,产生噪声污染,降低加工精度。因此,如何在保持高带宽的同时进行谐振抑制,已经成为提高伺服性能的一个关键课题。
关于机械谐振抑制,国内外学者已进行了大量研究,采用的方法主要分为两大方面:一方面从机械特性入手,通过修改机械结构或更改结构材料,以提高机械谐振的峰值频率或增加阻尼以降低谐振峰值:如增加电机转动惯量或降低负载转动惯量,改变传动结构或材料以提高传动刚性等,但其成本较高且适用范围窄;另一方面则是通过在伺服系统中加入控制器、滤波器等环节改善系统闭环特性来抑制机械谐振。该方式的谐振抑制策略主要分为以下几类:(1)通过增加传感器或状态观测器的方式引入状态反馈;其中,文献[13-14]均利用加速度反馈有效增加电机端惯性矩从而降低驱动对机械共振的敏感度;文献[15-19]是将负载对电机的扭转振动看作外部负载扰动,将负载观测器对负载端的扰动转矩观测值引入闭环系统进行补偿或前馈,提高系统的抗谐振能力,进而降低系统的速度波动;(2)根据已有数据进行输入信号整形,来抑制谐振,该方式属于被动抑制,通过将输入指令信号进行整形处理,消除指令信号中激发谐振的信号分量,从而实现减弱甚至消除谐振的效果;(3)在控制环路中串入低通或陷波滤波器调节相角裕度,减少谐振点处的增益,实现谐振抑制。其中,第三类方法由于需要的参数较少,算法简单且配置灵活,在实际伺服系统中运用最为广泛。为了准确获取谐振频率来配置滤波器,国内外学者提出了众多基于FFT的在线和离线谐振频率辨识的方法。但是由于阻尼、离散化和系统惯性的影响,实际系统所表现出的谐振频率会出现偏离自然谐振频率(Natural Torsional Frequency, NTF)的现象。对此,相关作者通过自适应陷波可很好提高算法的自适应性,但自适应陷波固有的调节过程会加剧系统震荡,甚至损坏传动装置。
基于以上分析,本文作者在机械谐振模型的基础上,重点分析了采样周期、阻尼和陷波器的串入对谐振状态的影响,解释了在线自适应陷波中频率配置错误下引起谐振频率偏移的原因,并得出在谐振出现偏移现象时最有效的陷波频率仍是系统自然谐振频率的结论,最后通过仿真与实验对理论分析进行验证。
1 谐振模型及谐振频率偏移现象
1.1 机械及控制模型
出于实际工况和生产成本的考虑,现实中的驱动电机、执行机构及传动机构组成的典型柔性传动双惯量模型如图1所示。其中:和为驱动电机和执行机构转动惯量;为传动轴阻尼系数;为电机转轴转角;为执行机构转角;与分别为电机和执行机构的转速;为电机电磁转矩;为负载转矩。由于电机和执行机构在力的作用下产生转角不同步,会使传动轴发生形变,为形变所产生的传动轴转矩,为传动轴扭转弹性系数。
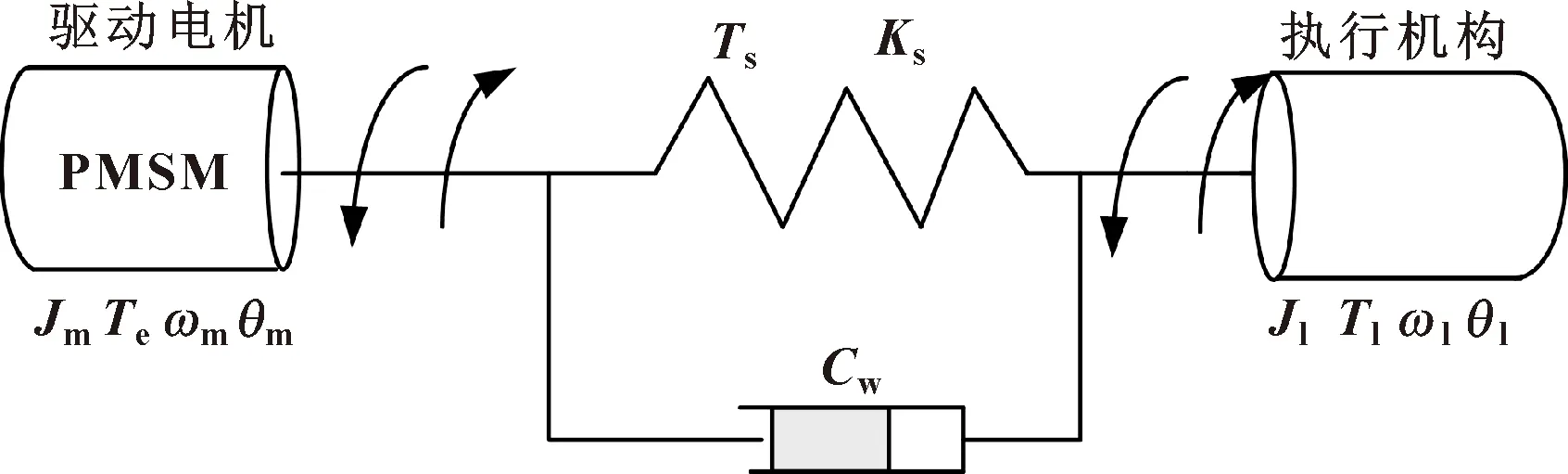
图1 双惯量系统模型
根据以上所设参数,可得到运动学方程组(1)及图2所示的系统控制框图。

图2 双惯量系统控制框图
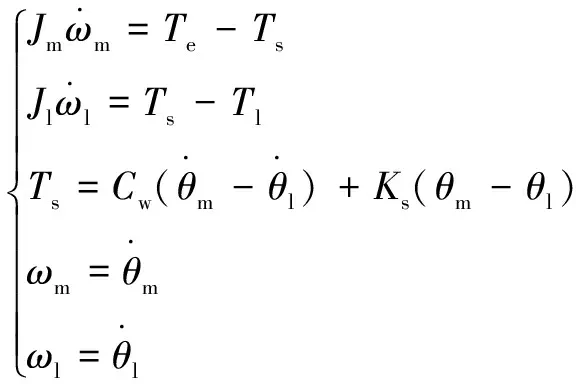
(1)
进而可得到电磁转矩、电机转速和负载转速之间的传递函数组:
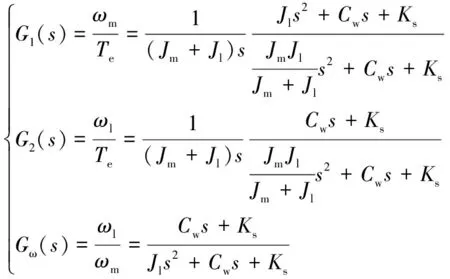
(2)
忽略相对较小的条件下,内存在两个谐振频率。其中的共轭零点为抗谐振频率点ARF(Anti-Resonance Frequency),共轭极点为自然振动频率点NTF。由式(2)可得出ARF与NTF表达式:

(3)
将数字伺服系统控制环路加以简化,设反馈环路为单位负反馈,电流环等效为时间常数为的一阶低通环节。由于重点在于分析谐振状态,取速度环控制器为比例控制器,输出限幅为±;同时使用零阶保持器来近似离散化环节,可以得整个伺服系统的连续控制回路框图如图3所示。其中为比例系数,为转矩系数,为速度环采样周期。

图3 离散系统控制框图
1.2 谐振频率偏移现象
根据图3,可得出离散系统的传递函数(4)

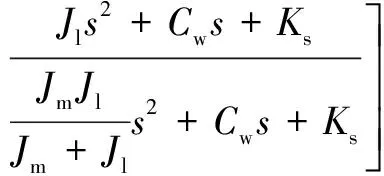
(4)
其中:为拉普拉斯算子;为采样时间。
取=0.56 N·m/A;=1×10s;=569 N·m/rad;=1.82×10kg·m;=1×10kg·m;=1×10s;= 0.01 N·m·s/rad;=6.59。该参数下系统的伯德图如图4所示[由式(3)可得=306 Hz]。由控制理论可知,增益裕度为负会导致系统不稳定,并且会产生穿越-180°处频率的谐振。因此,图4所示系统的谐振频率偏移至730 Hz(设系统所表现出的谐振频率为),并非306 Hz(NTF)。在高增益的数字伺服控制系统中,目前主要采用在速度环输出端串入改进双T形陷波滤波器进行谐振抑制,其传函和参数公式如式(5)所示,、和分别代表陷波频率、陷波宽度和陷波深度。

图4 离散系统伯德图

(5)
为了提高算法的鲁棒性,实际中会使用在线自适应的方法对陷波滤波器的陷波频率加以修正。但是在某些情况下,在线自适应陷波也会导致谐振频率的移动。选取速度环输出限幅为±6 A,陷波参数:=314 rad/s,=-40 dB,在图4系统中分别使用在线自适应陷波和陷波NTF两种算法,会存在如图5所示的现象:系统本身NTF为306 Hz,陷波前谐振频率已偏移至730 Hz。于0.1 s处启用自适应陷波滤波器,每0.1 s进行谐振频率辨识和陷波频率修正。在修正的过程中,谐振幅值刚开始有增大的趋势,系统所表现的谐振频率会逐渐接近NTF(在线自适应陷波下系统的当前谐振频率已在图中标出)。可见,当系统已经处于谐振频率偏移状态时,在线自适应滤波难以实现快速、平稳地谐振抑制。

图5 机械谐振频率偏移现象
2 谐振频率偏移现象成因
由图5可知,系统谐振频率偏移NTF的原因可分为两类:第一类是由于系统本身参数导致;第二类是人为加入陷波导致。从增益裕度角度出发,选取采样周期、阻尼和陷波3个影响系统相频特性的主要因素进行分析。
2.1 采样周期影响分析
在图4参数的基础上,取=0.01 N·m·s/rad,变化采样频率(1),得到不同采样频率下的系统开环伯德图如图6所示。虽然连续系统增益裕度为正,但由于离散化带来的相角滞后,各采样频率下离散控制系统皆处于不稳定的谐振状态。而且随着采样频率的降低,离散控制系统的相角滞后增大,系统的谐振频率会逐步从高频段向NTF靠拢。

图6 不同采样频率下系统开环伯德图
2.2 阻尼影响分析
在图4参数的基础上,取=1×10s,变化,得到不同阻尼系数下的系统开环伯德图如图7所示。图中的系统皆处于谐振状态。其中阻尼系数影响了相频曲线中NTF处的下降斜率,随着阻尼系数的增大,NTF处的骤降趋势会变缓,导致系统的谐振频率会逐渐向高于NTF的频段发生偏移。但是另一方面,阻尼的增大能够有效地衰减NTF处的幅值增益,对系统趋于稳定有一定的帮助。
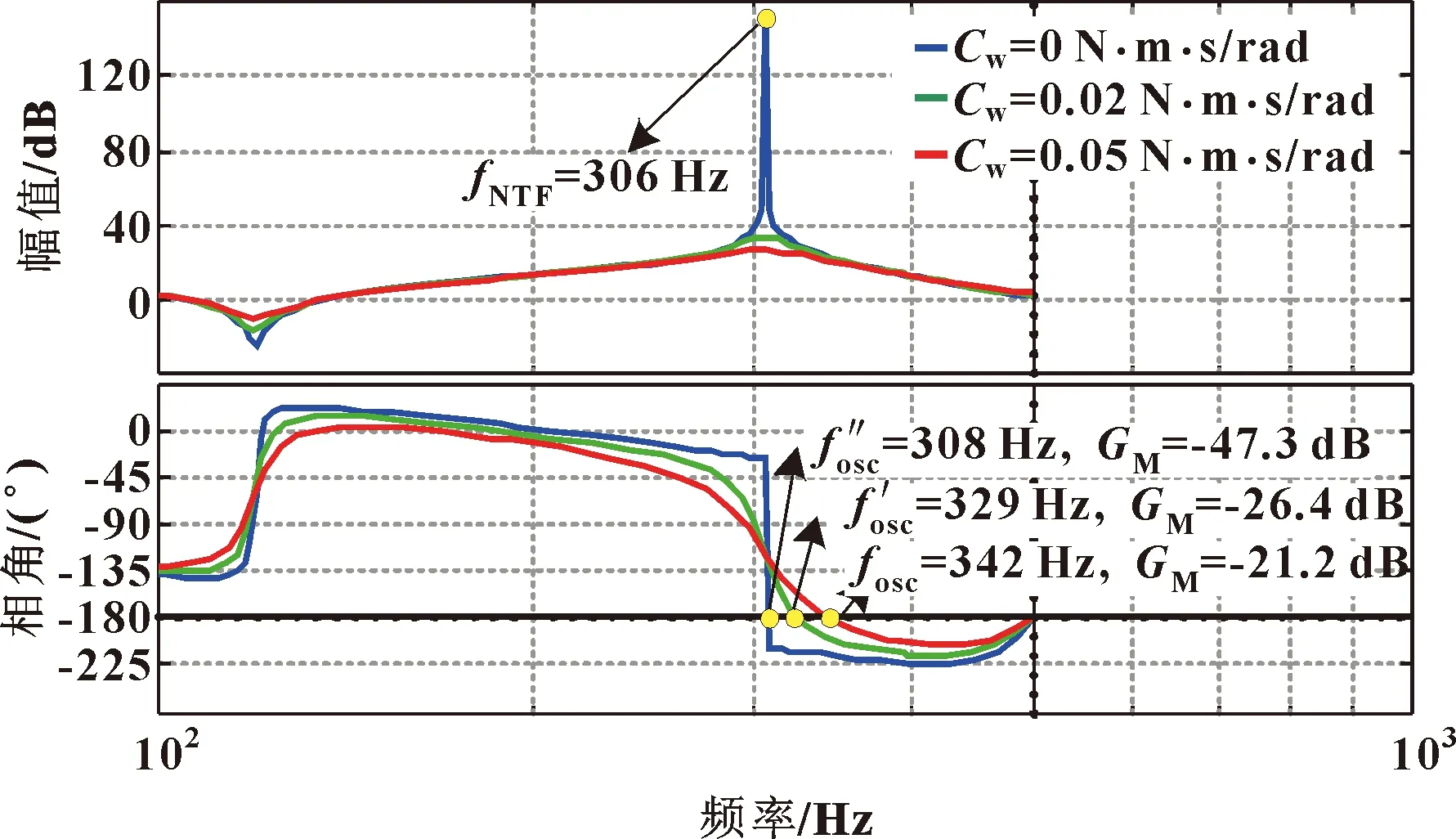
图7 不同阻尼系数下系统开环伯德图
2.3 陷波影响分析
在图4参数基础上,取=0.01 N·m·s/rad,=1×10s,陷波滤波器参数=314 rad/s、=-40 dB,得到不同陷波频率下系统开环伯德图如图8所示。系统自身NTF为306 Hz,表现出的谐振频率为730 Hz,陷波前已经处于谐振频率偏离NTF的状态。采用系统所表现的谐振频率进行两次1.2节所述的在线自适应陷波。根据陷波滤波器本身的相频特性可知,它在减少陷波频率往后频段相角滞后的同时,会加剧往前频段的相角滞后。因此,随着陷波频率的不断修正,系统所表现的谐振频率逐步向NTF靠拢,但是刚开始的修正过程也存在着增益裕度恶化现象,反映到时域即为谐振幅值的增大;而直接陷波NTF能够有效、快速地使系统恢复到稳定状态。

图8 不同陷波频率下系统开环伯德图
3 仿真验证
仿真中数字伺服系统的主要参数为:电机转动惯量1.82×10kg·m;负载转动惯量1×10kg·m;传动轴扭转弹性系数569 N·m/rad;电机额定功率750 W;电机额定电流3 A;电机定子电阻1.44 Ω;电机d、q轴电感为3.2×10H;转子磁链0.093 9 WB;极对数为4;母线电压300 V;电流环采样频率20 kHz;PWM载波频率10 kHz;速度环输出限幅6 A。通过选取不同的速度环采样周期和阻尼系数,在速度给定为2 000 r/min阶跃的情况下,得到谐振频率分布如图9(a)所示[由式(3)得NTF=306 Hz]。系统表现的谐振频率随着阻尼系数的增大而增大,逐渐远离NTF;随着采样周期的增大而减小,逐渐靠近NTF。
接下来选取=1×10s,=0.01 N·m·s/rad,陷波滤波器中取=2、=0.02,在转速给定为1 000 r/min阶跃的情况下,于0.2 s处进行1.2节所描述的基于系统表现的在线自适应陷波与基于传函的NTF陷波,陷波结果如图9(b)所示(陷波配置频率已在图中标出)。随着自适应陷波的进行,系统的谐振频率逐渐靠近NTF。在这个过程中,初始阶段存在谐振幅值增加的情况,当陷波频率接近NTF时,谐振现象逐渐收敛。

图9 仿真结果
而相较自适应陷波,直接陷波NTF能够更快速地完成谐振抑制,同时避免了谐振幅值增加对系统机械结构造成的劳损。综上可知,仿真结果与理论推导相吻合。
4 实验验证
柔性传动的对拖实验平台结构如图10所示。该实验平台的参数除负载转动惯量9.1×10kg·m,速度环输出限幅4 A,连接刚度为256 N·m/rad,谐振频率为190 Hz(通过系统平台的Chirp扫频测得)外,其他均与仿真参数相同。

图10 750 W PMSM的柔性传动研究实验平台
实验的第一部分用于验证谐振频率偏移。由于阻尼系数是固定的常数且难以调整,因此仅记录速度环在不同采样周期下的谐振频率。在图11(a)中,随着速度环的采样周期从0.5 ms到1.5 ms逐步递增,谐振频率从230 Hz到190 Hz逐步递减,这与第3节中的分析一致。
在第二部分实验中,将陷波器分别按照谐振频率(在线自适应滤波器)设定以及按照自然谐振频率NTF设定进行比较(设定=05,=0.02)。在图11(b)中,系统振荡频率为230 Hz。当陷波器频率设定230 Hz时,系统仍然不稳定,并且产生了一个新的谐振频率,该频率减小为210 Hz。当调整陷波频率为190 Hz时系统最终稳定。相反,如果陷波频率设定为NTF时,系统快速稳定下来并且无需自适应陷波器的自适应调节过程。图11(b)同样验证了该结论,当谐振频率大于自然谐振频率NTF时,按照谐振频率进行设定陷波频率会导致一个新的且更低的谐振频率出现。

图11 实验结果
5 结语
针对数字伺服系统机械谐振频率偏移现象,文中重点分析了采样周期、阻尼和陷波对谐振频率的影响,解释了系统在未加陷波滤波器时所体现的谐振频率与NTF不符以及陷波滤波器的串入造成谐振频率移动的原因,并给出了谐振频率偏移状态下陷波NTF的解决方案。虽然现实系统往往无法提前获取NTF等信息,只能在线获得实际谐振频率值,但文中的机制分析解释了谐振频率偏移的现象。仿真和实验结果证明了理论分析的正确性和有效性。在谐振频率偏移的情况下,快速实现NTF辨识,将是下一步研究的重点。
