定向渗流诱导的非均质冻结壁力学特性分析

王彬，荣传新，程桦，蔡海兵

（1.安徽理工大学土木建筑学院，安徽 淮南 232001；2.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001；3.安徽理工大学安全科学与工程博士后科研流动站，安徽 淮南 232001；4.中煤矿山建设集团有限责任公司博士后科研工作站，安徽 合肥 230091）

0 引言

冻结壁作为拟开挖土体周围的临时支护结构其受力特性分析一直是人工地层冻结法研究领域的重要问题。在该问题的研究初期，冻结壁被视为均质材料，其力学分析过程被简化为厚壁圆筒的受力问题［1］，该分析方法较为简单，因此被工程上广为应用［2-3］。然而由于受冻结管热传导距离的影响，冻结壁内部的温度并不相等，而是随着与冻结管的距离的变化而变化［4-5］，这导致冻结壁内部的强度是不均匀的，因此将冻结壁视为均质材料进行计算存在一定误差。胡向东等［6-7］首次提出将冻结壁视为功能梯度材料，并基于摩尔-库伦强度准则推导了单排管以及双排管冻结壁的应力计算公式；王彬等［8-9］根据该思路并基于D-P强度准则也对单排管以及双排管冻结壁的应力公式进行了推导，并首次提出了三排管非均质冻结壁的应力计算公式［10］；曹雪叶等［11-12］基于双剪统一强度准则推导得出了材料性质呈抛物线变化的FGM冻结壁的应力计算公式。由于冻结壁并不是单独存在于土体中的，因此冻结壁周围的未冻土体与冻结壁之间存在相互作用，并且冻结壁内部土体开挖会对冻结壁的受力状态产生一定的影响，杨维好等［13-15］推导得出了考虑与围岩相互作用的冻结壁弹性、弹塑性以及塑性应力解；胡向东等［16-18］推导得出了考虑开挖卸载作用的冻结壁承载力的计算公式；王彬等［19］基于上述理论，推导得出了考虑卸载作用以及与周围未冻土体相互作用的非均质冻结壁的应力计算公式。

流动的地下水作用下人工冻结温度场的分布规律与无流速时相比存在较大差异［20-25］，其中位于上游区域的冻结壁厚度明显小于下游区域，冻结壁不再是一个规则的厚壁圆筒，传统的“厚壁圆筒”分析方法不再适用；并且冻结壁内部的温度分布规律也发生了较大变化，位于冻结管布置圈上游以及下游的温度场存在明显差异［20-22］，因此现有的温度曲线等效方法［6-7］也不再适用。同时，现有文献中关于冻结壁弹塑性分析的研究，通常只采用一种屈服准则进行推导与计算［6-10］，不能全面地反映出冻结壁的力学特性。针对上述问题，本文将基于定向渗流诱导的非均质冻结壁温度场的分布规律，考虑不同的冻土强度准则，对定向渗流诱导的非均质冻结壁的应力计算公式进行推导，并结合工程算例对不同流速作用下的冻结壁的力学特性进行计算分析。

1 定向渗流诱导的非均质冻结壁温度场分布规律

在流动的地下水作用下，位于上游位置的冻结壁最迟交圈，对应相同的冻结时间，该位置的冻结壁厚度最小，且同时受到地层压力以及水压的作用，因此该位置是整个冻结壁“最危险位置”，该位置冻结壁的强度决定了整个冻结壁的稳定性。已有研究成果表明，在无流速时，冻结壁截面的温度最低点位于冻结管布置圈上；而定向渗流诱导的非均质冻结壁“危险截面”的温度最低点位于冻结管布置圈下游位置处［23］；同时，二次函数可以较好地反映相邻冻结管中间区域截面的温度场分布规律［6-11］。因此，为了便于采用数理方程描述“危险截面”的温度分布规律，以冻结温度场最低温度点所在位置作为冻结壁分区界线，分别用两段二次函数曲线近似替代温度场的分布曲线［6-11］。

不同流速的地下水作用下冻结壁“危险截面”的温度曲线计算模型如图1所示。将冻结壁的内径用R0表示，拟开挖边界的半径用R1表示，冻结壁的外径用RH表示，冻结壁截面上任一点的半径用R表示。为了便于公式的推导，用相对半径r=R/R0表示冻结壁截面内的任一点。

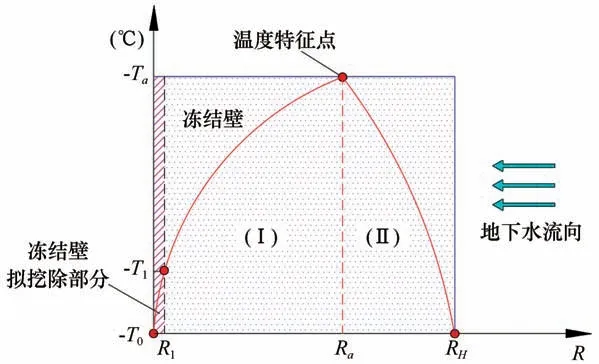
图1 不同流速的地下水作用下冻结壁温度分布模型Fig.1 Temperature distribution of the"dangerous section"of the frozen wall under the action

在冻结壁内径处：R0/R0=1；

在冻结壁拟开挖边界处：R1/R0=r1；

在冻结壁外径处：RH/R0=rH；

假设冻结壁“危险截面”的温度分布规律满足以下二次函数表达式：

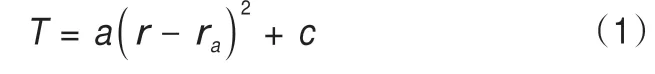
式中：ra为截面温度最低点所在位置；a、c为待定常数。

温度场的边界条件为：

式中：T0（℃）为土体的冻结温度，即冻结锋面处冻土的温度；T1为冻结壁拟开挖边界的控制温度，该温度一般为-3℃；Ta（℃）为冻结壁截面的最低温度，Ta与地层中水流速度V相关。

将边界条件（2）代入（1）可得冻结温度场的曲线函数为：

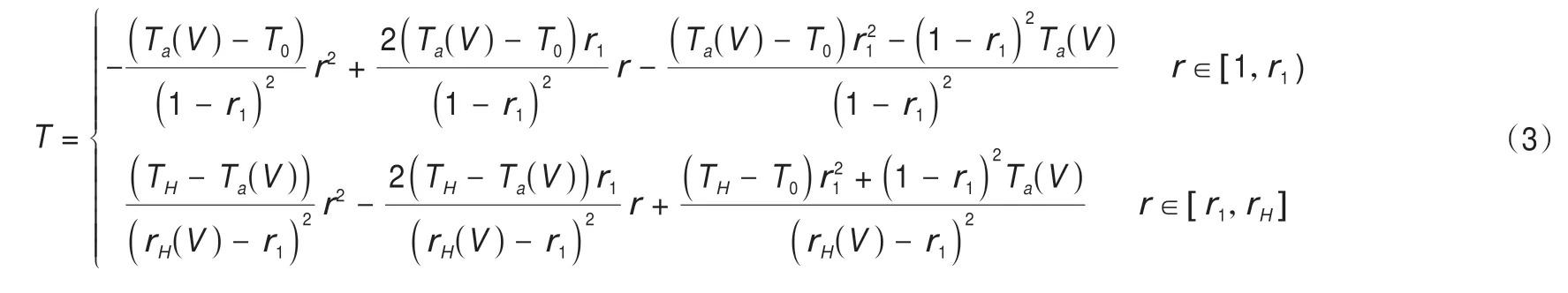
2 冻土力学特性

2.1 冻土强度参数

已有研究成果表明，不同土性冻土的弹性模量E、黏聚力c与温度存在近似的一次函数关系［19］。

结合冻结壁“危险截面”温度场的分布规律，将冻结壁的弹性模量以及黏聚力用二次函数［6-11］表示：

式中：a1，a2，b1，b2，d1，d2以及m1，m2，n1，n2，l1，l2分别是与温度分布曲线相关的参数，且上述参数都是与地下水流速V相关的参数。

假设冻结前后土体的泊松比μ与内摩擦角φ保持不变［6-8-19］。

2.2 冻土强度准则

认为冻结壁进入塑性后体积不可压缩，对于轴对称平面应变问题有［13-15］：

因此几种常用的强度准则经推导后可以用下式表示［14-15］：

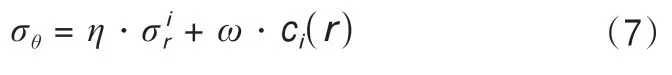
式中：η以及ω的表达式如表1所示。

表1 不同屈服准则中η以及ω的表达式Table 1 Expressions ofηandωin different strength criteria

3 冻结壁应力计算公式

3.1 地下水作用下冻结壁力学模型

为了便于计算，将受流动的地下水影响形成的不规则的冻结壁简化成厚度与“危险截面”相等的厚壁圆筒。冻结壁“危险截面”的力学模型如图2所示。

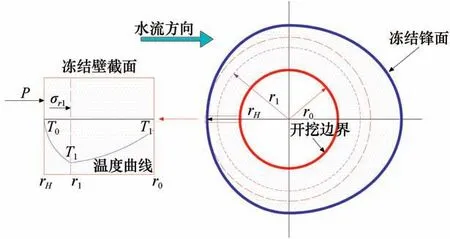
图2 地下水作用下冻结壁“危险截面”力学模型Fig.2 Mechanical model of"dangerous section"of frozen wall under groundwater

考虑开挖卸载作用后，无穷远处未冻土体的等效应力［16-18］为：

式中：P为土体的原始水平应力；μ0为土体的泊松比。

在力学模型中，冻结壁的应力场边界条件为：

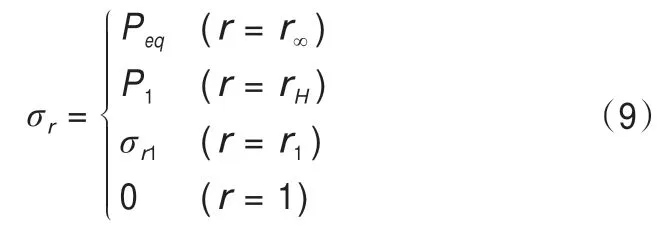
3.2 冻结壁弹性应力计算公式

当冻结壁处于弹性平面应变状态时，满足以下基本方程：

平衡方程［26］：

几何方程［26］：

平面应变状态下的物理方程［26］：

引入应力函数ψ，将σr，σθ通过ψ表示［6-9］：

结合式（10）～（13）可得：

将冻结壁周围未冻土体视为均匀、弹性介质，则周围土体的弹性应力计算公式［26］为：

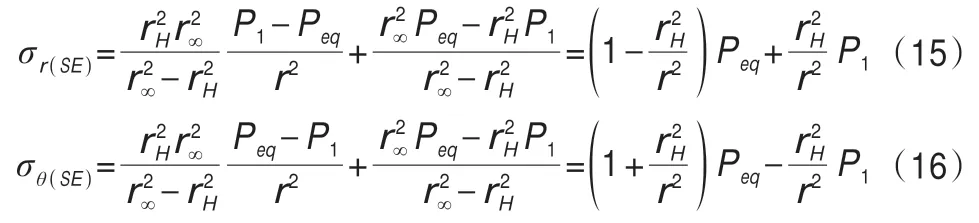
由（4）可知，冻结壁的弹性模量随着r变化，将弹性模量E（r）表达式代入（14）可得：

通过求解可以得出（17）的通解为：

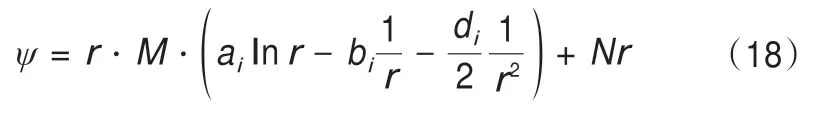
式中：i=1，2分别表示靠近开挖边界一侧以及靠近未冻土体一侧。

将应力边界条件带入（18）可以得到靠近开挖边界一侧的冻结壁弹性应力计算公式为：

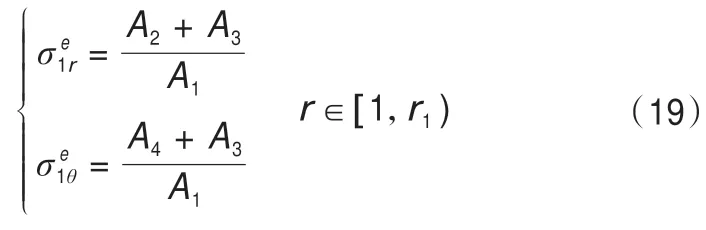
同理，可以得到靠近未冻土体一侧的冻结壁弹性应力计算公式为：

冻结壁rH以及r1处的位移连续条件为：

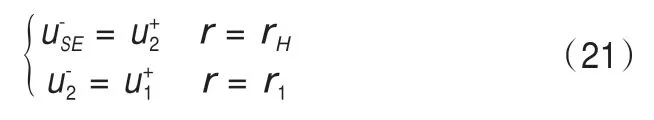
在平面轴对称问题中有：

因此可以得出下式：

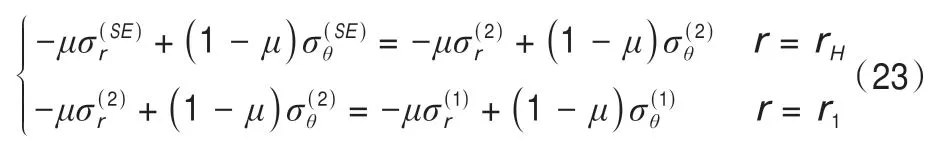
由方程（23）可以求得P1以及σr1。

3.3 冻结壁弹塑性应力计算公式

当冻结壁的外荷载大于冻结壁的弹性极限承载力时，冻结壁进入弹塑性状态，沿着冻结壁“危险截面”由内向外依次分为塑性区以及弹性区。

塑性区应力平衡方程为［27］：

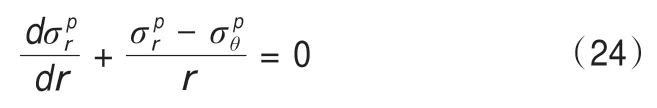
将强度准则代入（24）得：

通过求解可以得出冻结壁塑性区径向应力的通解为：

根据r=1以及r=r1处的应力边界条件可以求得Ci的值为：

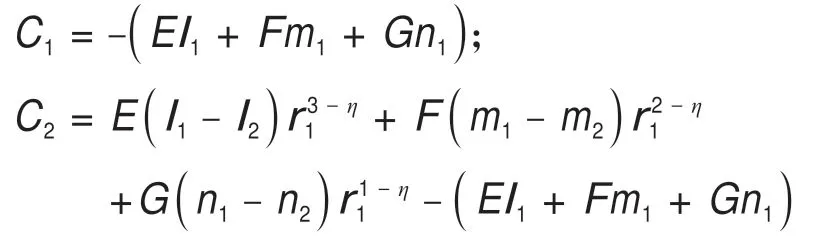
冻结壁塑性区的环向应力可以通过下式求得：

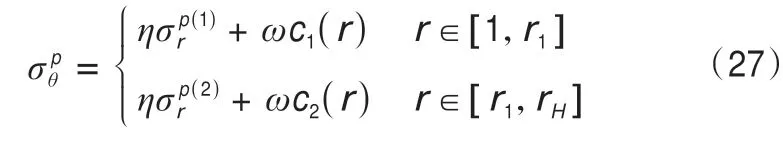
假设冻结壁塑性区半径为ρ。当ρ∈[1，r1)时，在区间[1，ρ)上，冻结壁处于塑性状态；在区间[ρ，rH]上，冻结壁处于弹性状态。冻结壁的应力计算公式为：

当ρ∈[r1，rH]时，在区间[1，ρ)上，冻结壁处于塑性状态；在区间[ρ，rH]上，冻结壁处于弹性状态。冻结壁的应力计算公式为：

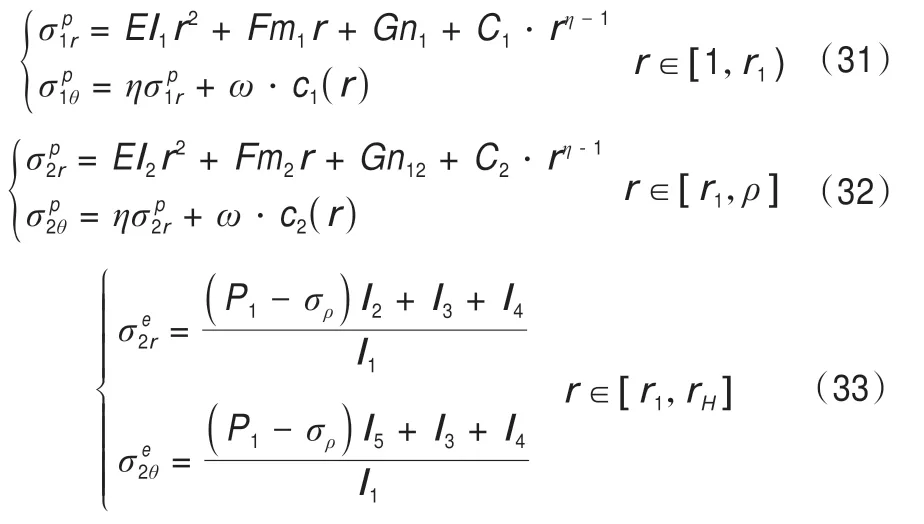
由上述公式可知，当塑性区半径ρ=1以及ρ=rH时，对应的冻结壁外荷载分别是冻结壁的弹性极限承载力以及塑性极限承载力。

3.4 冻结壁塑性区半径求解

在r=ρ处，冻结壁应力满足应力连续条件，即

塑性区半径可由式（35）、（36）分别联立（35）求得。

4 工程算例分析

淮南矿区潘一矿中央风井的冻结孔布置方案以及冻土力学参数分别如表2～3所示［25］。

表2 潘一矿中央风井冻结孔设计参数Table 2 Freezing parameters of central wind shaft in Panyi Mine

基于上述参数，通过水热耦合数值计算模型（该计算模型的合理性已经得到文献［25］的验证），采用COMSOL Multiphys数值计算软件对不同流速条件下冻结壁危险截面的温度分布规律进行计算，计算结果如图3所示。

图3 地下水作用下冻结壁“危险截面”的温度分布规律Fig.3 The temperature distribution law of the"dangerous section"of the frozen wall under the action of groundwater at different flow rates

对开挖前冻结壁的厚度随流速的变化规律进行拟合，如图4所示。

图4 冻结壁厚度随地下水流速变化规律的拟合曲线Fig.4 Fitting curve of freezing wall thickness with the change of groundwater velocity

由拟合结果得出冻结壁厚度L与地下水流速V的关系式为：

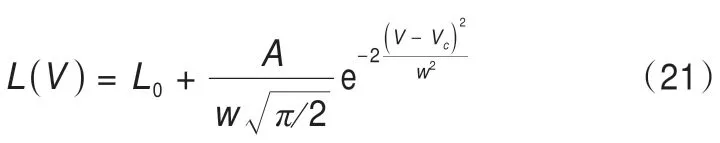
式中：L0、A、w以及Vc为拟合参数。

冻结壁的厚度也可以表示为：

通过数值计算得出冻结壁“危险截面”上温度曲线的计算参数如表4所示。

表4 冻结温度场计算参数Table 4 Calculation parameters of freezing temperature field

将温度场的计算参数带入公式（3）可得出不同流速条件下冻结壁危险截面上温度场计算公式，随后根据表3中冻土力学参数与温度的关系，得出冻结壁“危险截面”上弹性模量以及黏聚力随半径的变化规律。将弹性模量以及黏聚力带入对应的应力计算公式，即可得出冻结壁应力计算公式。

表3 冻土力学参数Table 3 Mechanical parameters of frozen soil

图6 冻结壁塑性极限承载力计算结果Fig.6 Calculation results of plastic ultimate bearing capacity of frozen wall

不同流速的地下水作用下冻结壁的弹性极限承载力以及塑性极限承载力的计算结果如图5～6。通过分析可以发现：基于不同屈服准则的冻结壁的承载力的计算结果存在一定的差异，其中基于M-C准则以及D-P准则的计算结果基本一致，基于广义Tresca准则的结果略大于M-C准则以及D-P准则的计算结果，而基于双剪强度准则的计算结果则明显偏大。冻结壁的承载力随着水流速度的增大而减小，当地下水流速为5 m·d-1时，基于M-C准则、D-P准则、广义Tresca准则、双剪准则计算得出的弹性极限承载力以及塑性极限承载力分别为2.480、2.462、2.741、3.202 MPa以及4.349、4.318、4.561、5.779 MPa，当地下水流速增加至10 m·d-1时，对应的弹性极限承载力以及塑性极限承载力降低至2.087、2.085、2.203、2.784 MPa以及3.700、3.707、3.908、4.939 MPa。

图5 冻结壁弹性极限承载力计算结果Fig.5 Calculation results of elastic ultimate bearing capacity of frozen wall

弹性极限状态以及塑性极限状态下冻结壁的应力分布曲线如图7～8所示。由于位于冻结壁分区界线（r=1.685）两侧的冻土力学参数存在较大差异，因此位于分界线两侧的冻结壁的应力分布规律也存在较大差异。当冻结壁处于弹性极限状态时，冻结壁的径向应力随着相对半径r的增大而增大，而环向应力的分布则具有明显的区域差异性。当r＜1.685时，环向应力曲线呈抛物线形状，曲线随相对半径r的变化较为缓慢；当r＞1.685时，由于地下水的影响该区域冻结壁的厚度较小，温度变化梯度较大，因此该区域冻结壁的环向应力随着相对半径的增加而急剧降低；弹性极限状态下，冻结壁的环向应力的最大值出现在靠近冻结壁中间的位置。当冻结壁处于塑性极限状态时，冻结壁的径向应力随着相对半径r的增大而增大，环向应力的分布具有明显的区域性。当r＜1.685时，环向应力随着相对半径r的增大而增大；当r＞1.685时，冻结壁的环向应力随着相对半径的增加而急剧降低；塑性极限状态下，冻结壁的环向应力的最大值出现在冻结壁的分区界线r=1.685处。

图7 弹性极限状态下冻结壁应力分布曲线图Fig.7 Stress distribution curve of frozen wall under elastic limit state

5 结论与讨论

（1）将大流速渗透地层中冻结壁最迟交圈的位置视为“危险截面”，通过分段等效的方法结合温度特征点，得出该截面的温度曲线表达式；根据冻土力学参数与冻结温度的线性关系，将冻结壁视为随温度函数变化的非均质材料；分别基于M-C准则、D-P准则、广义Tresca准则及双剪强度准则，推导得出渗流场作用下单排管非均质冻结壁应力计算公式。

图8 塑性极限状态下冻结壁应力分布曲线图Fig.8 Stress distribution curve of frozen wall under plastic limit state

（2）基于不同屈服准则的冻结壁承载力的计算结果存在一定的差异，其中基于M-C准则以及D-P准则的计算结果基本一致，基于广义Tresca准则的结果略大于M-C准则以及D-P准则的计算结果，而基于双剪强度准则的计算结果则明显偏大。

（3）冻结壁的承载力随着水流速度的增大而减小，当地下水流速为5 m·d-1时，基于M-C准则、D-P准则、广义Tresca准则、双剪准则计算得出的弹性极限承载力以及塑性极限承载力分别为2.480、2.462、2.741、3.202 MPa以及4.349、4.318、4.561、5.779 MPa，当地下水流速增加至10 m·d-1时，对应的弹性极限承载力以及塑性极限承载力降低至2.087、2.085、2.203、2.784 MPa以及3.700、3.707、3.908、4.939 MPa。

（4）当冻结壁处于弹性极限状态时，冻结壁的径向应力随着相对半径r的增大而增大，环向应力的分布具有明显的区域差异性。当r＜1.685时，环向应力曲线呈抛物线形状，应力曲线随着相对半径r的变化较为缓慢；当r＞1.685时，由于地下水的影响该区域冻结壁的厚度较小，温度变化梯度较大，因此该区域冻结壁的环向应力随着相对半径的增加而急剧降低；弹性极限状态下，冻结壁的环向应力的最大值出现在靠近冻结壁中间的位置。

（5）当冻结壁处于塑性极限状态时，冻结壁的径向应力随着相对半径r的增大而增大，环向应力的分布具有明显的区域差异性。当r＜1.685时，环向应力随着相对半径r的增大而增大；当r＞1.685时，冻结壁的环向应力随着相对半径的增加而急剧降低；塑性极限状态下，冻结壁的环向应力的最大值出现在冻结壁的分区界线r=1.685处。

（6）本研究将定向渗流诱导的非均质冻结壁简化为受均布荷载、厚度与危险截面处冻结壁相等的“厚壁圆筒”，并基于四种冻土强度准则对不同流速条件下冻结壁的力学特性进行了计算分析，所得出的结果反映了冻结壁最危险状态下的力学特性，能够为大流速渗透地层冻结壁的设计提供一定的参考。但是，受理论解析方法的限制，该模型仅能反映进入稳态的冻结壁的力学特性，没有考虑水-热-力耦合作用，我们将在后续的研究中采用数值计算的方法对该问题展开进一步深入的探索。