山地冰川变化的数值模拟及其在亚洲高山区的应用

段克勤，石培宏，何锦屏

（陕西师范大学地理科学与旅游学院，陕西 西安 710119）

0 引言

在全球气候日益变暖背景下，全球山地冰川普遍呈减薄后退状态［1］，引发社会各界对冰川这一固体水库的储存量及其变化的关注。亚洲高山区（青藏高原及其周边高海拔地区），因其巨大的海拔高度和特殊的地理位置，拥有中低纬度最多的冰川。这些冰川是亚洲大江大河的重要水源地，冰川退缩的直接后果就是淡水资源的减少［2-3］，而且冰川的快速退缩还引起了诸如冰湖溃决等自然灾害［4-5］，以及河川径流的季节性改变［6-8］。亚洲高山区正处于快速变暖过程中［9-10］，造成冰川大幅度退缩［11-15］。在当前全球持续变暖背景下，明确亚洲高山区冰川未来变化趋势及幅度，对揭示亚洲高山区水塔失衡失稳的科学内涵、过程机理、减缓和应对这一演化趋势，具有十分重要的科学意义和应用价值。

中国科学家自20世纪50年代开始研究亚洲高山区冰川以来，不论是定点观测研究，还是利用卫星遥感资料进行空间上的研究，迄今已取得了巨大成绩，特别是中国第一和第二次冰川编目的完成［15］，以及长期观测冰川变化的数据积累［16］，在亚洲高山区冰川变化方面做了大量的工作，扩展和丰富了亚洲高山区的冰川研究内容，为深入研究亚洲高山区冰川变化奠定了基础。然而，同国际同行相比，我国的冰川研究相对偏重于实地观测和统计分析，而缺乏对冰川变化的机理与理论研究，特别是利用数值模拟方法对冰川变化的研究，与发达国家还存在较大差距。

随着研究的深入，为明确冰川-气候-水文之间的定量联系，以及揭示冰川对气候变化响应机理，并预测冰川的未来变化趋势，应用物理模型对冰川变化进行模拟和预测是必然的发展趋势。在老一辈冰川学家施雅风和谢自楚等，以及秦大河、姚檀栋和丁永建等冰川学家的大力推动下［17-19］，开展冰川变化的数值模拟研究已是我国冰冻圈研究的重要领域和趋势［18，20］。虽然国内学者最近在冰川变化模拟方面取得了显著研究进展［20-25］，然而如何利用完全的物理模型定量的对冰川变化进行全面深入的分析，并在此基础上进行更科学的预测，与发达国家相比，还存在较大差距。因此，推动冰川变化的数值模拟研究，不仅可以深刻揭示山地冰川变化规律，而且可以推动中国的冰川研究向数值化方向发展，以缩小与发达国家的差距，相关研究急需加强。

本文介绍了冰川数值模拟的基本原理和方法，综述了近年来亚洲高山区冰川数值模拟的研究现状，基于目前的研究与认识，提出亚洲高山区冰川数值模拟研究的薄弱环节并进行了展望。

1 冰川变化数值模拟的基本原理

冰川是特定气候在特殊地形下的产物。作为一个巨大的非牛顿流体，重力使其总处于持续运动状态。由物质守恒定律，可以得到冰川表面厚度变化的控制方程：

式中：H为冰川厚度；V是冰川运动速度；t为时间；b为物质平衡。

式（1）表示冰川某处的厚度变化由两部分决定：一是发生在此处冰川表面的物质平衡，二是此处冰流通量的散度变化。在重力作用下冰川总处于运动之中，造成冰川物质处于不断调整和分配中。当冰川物质平衡为零时，消融区损失的物质会由冰川上部积累区向下输送物质而得到补充，使冰川总处于动态平衡中。但当冰川消融加剧，消融区扩大而积累区缩小时，向下输送的物质会减少，冰川消融区因得不到足够物质补给，会造成冰川退缩减薄，反之则冰川变厚并引起末端前进（图1）。因此，冰川对气候的响应过程就是在地形约束下，冰川物质平衡过程和冰川动力过程相耦合的动态演变过程，只有从冰川表面的物质平衡和冰川流动两方面考虑，才能完整刻画冰川的动态变化。

图1 冰川动态变化示意图（A.纵剖面图；B.俯视图）Fig.1 Sketch map of glacier dynamic change（A.vertical section view；B.bird view）

基于此，模拟冰川变化的经典方案如图2所示。要对一个冰川进行全面的研究，需从三个方面入手：一是冰川变化的气候背景，即冰川及其周边的气象条件是什么；二是冰川对气候响应过程，这不仅要充分考虑发生在冰川表面的物质平衡过程，还要考虑冰川流动引起的物质辐合辐散过程；三是冰川变化的影响问题，如冰川融水对河川径流的影响。

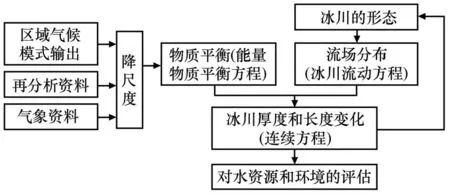
图2 冰川变化模拟的经典方案流程图Fig.2 Flow chart of glacier variation simulation

2 冰川物质平衡模拟进展与方法

在式（1）中，冰川物质平衡b是指冰川表面各种相态水收支的代数和，是冰川发育水热条件的综合反映，是衔接冰川变化与气候变化之间关系的重要参量。冰川物质平衡观测主要基于冰川表面花杆/雪坑法，在过去几十年对中国西部典型冰川进行了大量的物质平衡观测，积累了宝贵的资料［11，16］。随着多源遥感资料日益丰富，利用大地测量法获取冰川变化信息，已成为研究冰川物质平衡变化的主要手段［16，26］。近年来发展的三维激光扫描和无人机等新技术，也为研究冰川物质平衡变化提供了新的重要手段［20］。

但要深入研究冰川物质平衡对气候的响应及未来变化趋势，必须依赖于基于物质平衡变化过程的数学模型。目前主要有两类模型用来研究冰川物质平衡：一是基于参数化的温度指数模型［27-28］（以下称：温度指数模型）；二是详细描述冰川表面物质能量平衡过程的模型（以下称：能量平衡模型）［21，29］。能量平衡模型所需要参数较多且不易观测，目前只在观测要素全面的个别冰川得到应用，国内一般都是依据气象观测计算单点的物质平衡［30］。相比较，温度指数模型参数化程度较高，应用比较广泛［31-32］。但利用物质能量平衡模型可深入揭示冰川物质平衡变化的原因及其对气候响应方式。为了更加准确描述冰川的时空变化，如考虑地形因素及其对太阳辐射的遮蔽等，国际上已发展出分布式物质能量平衡模型［29，33］。模型也从冰川表面物质平衡的简单模拟，向考虑冰川表面不同介质（例如积雪、粒雪、冰川冰和表碛物等）和不同层位（将表面能量平衡和冰面以下雪冰过程）相耦合的复合模型方向发展，使物理基础更加健全和精细，如COSIMA［34］和COSIPY［35］模型。当前国际上另一个发展动态是利用再分析资料（例如EAR5、NCEP等）和区域气候模式结果作为输入驱动数据，通过求解物质能量平衡方程，模拟分析一个流域或更大范围的冰川物质平衡变化，而不局限单个冰川［36］。并在此基础上，基于气候预估数据（如CMIP6），利用物质能量平衡方程实现评估区域尺度冰川变化［37］。这方面的研究非常有助于从整体上认识大范围和流域尺度内冰川变化及其水文水资源变化。

国内能量物质平衡的研究源自20世纪50年代开始的山地冰川冰/雪能量平衡与转化研究［38］。近年来随着参数化方案的不断完善，能量物质平衡模型在亚洲高山区快速被应用。如在珠穆朗玛峰东绒布冰川［39］、祁连山七一冰川［40］和老虎沟12号冰川［23］、念青唐古拉山西布冰川和扎当冰川［41］、帕米尔［30］以及藏东南帕隆藏布4号冰川［42］等开展了基于能量物质平衡模型的冰川模拟研究。以上工作验证了能量平衡模型能够精准地模拟冰川消融过程。但是目前国内物质能量平衡的研究，主要是以单点或单条冰川为主。虽然基于度日模型的流域/区域研究已经在祁连山北大河流域和阿尔泰山地区已有应用［43-44］，但对整个流域或一个区域内冰川分布式物质能量平衡模拟研究工作还尚未系统开展。值得尽快开展这一方面的研究，以缩小与国际同行之间的差距，并为评价冰川变化对水资源的影响奠定坚实基础。

能量物质平衡模型可用下面的公式描述［29］：

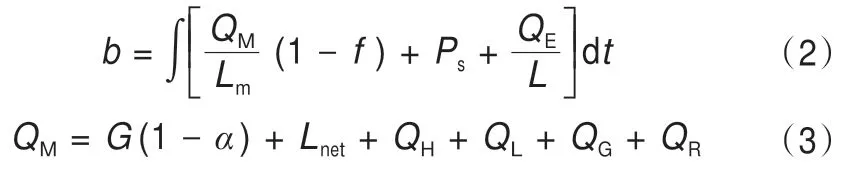
式中：b为物质平衡；QM为冰川表面消融耗热；Lm为冰的融化潜热；f为冰川融水再冻结量；QE为升华或蒸发耗热；L为升华或蒸发潜热；Ps为固态降水；G为太阳辐射；α为反射率；Lnet为净长波辐射通量；QH为显热通量；QL为潜热通量；QG为地面热通量；QR为降水带来的热量。这些物理量通常都难以直接获得，只能通过参数计算，目前这方面的理论研究比较充分，有完备的计算方法，关键是如何获得研究区气象要素的空间分布。对分布式物质能量平衡模型而言，除气象资料外，还必须考虑诸如地形对辐射的遮蔽等因素［21，29］。

驱动分布式物质能量平衡模型，需要空间变化数据。气象台站资料比较稀疏，而同化后的再分析资料如NCEP和EAR5，分辨率又比较低，不能直接用于分布式物质能量平衡模型。因此，需要把气象资料和再分析资料降尺度到研究区域。方法一，把气象站资料和再分析资料利用统计方法（例如偏差校正）插值到空间格点［29，31，45］；方法二，利用气候模式对再分析资料，以及全球气候模式的模拟结果进行动力降尺度，把各气象要素（温度、降水、辐射、湿度、风速和气压）降尺度到研究区域［46-47］。受限于观测资料和再分析资料自身不确定性的限制，降尺度（统计或动力）在面向单条冰川或流域/区域冰川模拟时存在一定的误差［20，48］。但对于长时间尺度冰川物质平衡的模拟，使用降尺度后的数据能够较好重现观测结果［49-51］。

最后由数字化地形图确定冰川范围，划分冰川区计算网格，确定每个网格的高程、坡向和坡度，结合网格化的各气象数据，代入物质能量平衡方程，计算每一个格点的物质平衡变化，探讨冰川物质平衡对气候变化的响应。

3 冰川流动模拟进展

冰川流动会造成物质迁移，改变冰川的水热、边界条件，使冰川形状不断发生调整，并决定冰川末端的变化速率。因此，冰川的流动极大增加了冰川变化研究的复杂性。

冰川冰通常认为是不可压缩、黏性的能导热的非牛顿流体，则式（1）中的描述冰川的动量守恒方程为：

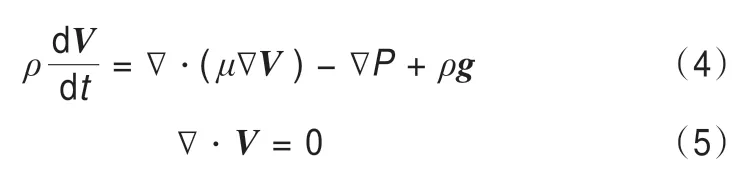
式中：P为压力；η为动力学黏性系数；ρ为冰的密度。

在20世纪60—70年代，对冰川流动的研究主要采用浅冰近似模型，如采用一维浅冰近似流线模型模拟了挪威Nigardsbreen冰川末端变化［54］。20世纪80—90年代，二维冰流模型在山地冰川动力学过程中得到了广泛使用［55-58］。进入21世纪后，随着计算能力的提高和理论研究的深入，应用有限元方法求解三维的Stokes方程模拟冰流过程取得了进一步进展，如用非常复杂的三维冰流模型成功模拟了瑞士Rhonegletscher冰川和Grosser Aletschgletscher冰川的变化历史，并对冰川变化进行了预测［59］。整体而言，尽管现有动力学模式都是建立在冰川流动定理与物质守恒原理之上，但使用了不同的关系式和简化方法，区别在于是选择全Stokes方程进行计算，还是采用全Stokes方程的简化近似模型进行计算［60-64］。

在国内早期针对新疆天山乌鲁木齐河源1号冰川进行过频率响应［65］和主流线厚度简单模拟［66］，以及对新疆伊犁河流域冰川的一些理论性探讨研究［67］。近年来，段克勤等［22］利用有限元算法对二维的Stokes方程求解，计算了乌鲁木齐河源1号冰川的流动速度，发现模拟结果与实测速度非常吻合。李慧林［68］利用“浅冰近似（SIA）”对天山乌鲁木齐河源1号冰川进行了模拟和预测。

国内冰川流动模型研究近年最大的亮点是张通等［25］和王玉哲等［63］发展了PoLIM冰川流动模型，其核心控制方程为：

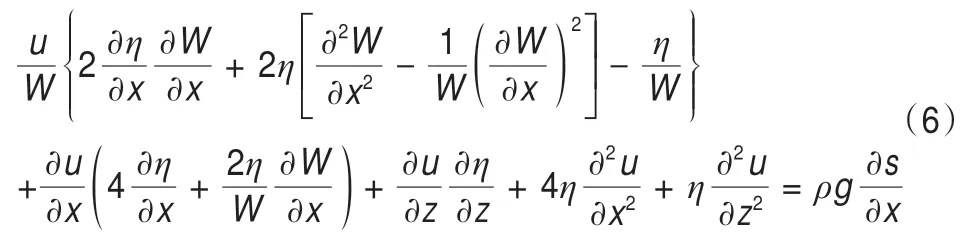
式中：u是水平速度；W是冰川宽度；s是冰川表面高程；η是黏性系数，定义如下：

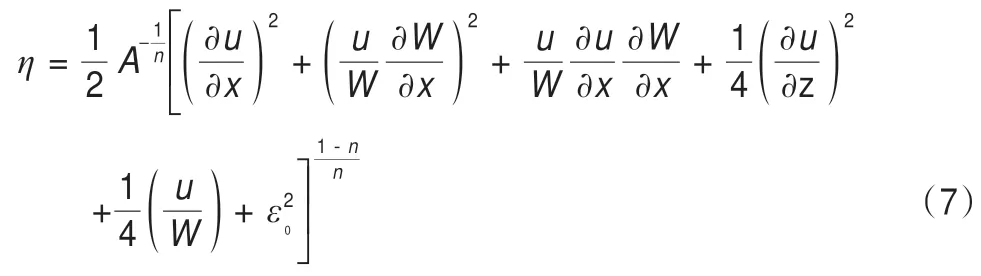
即冰的有效黏性系数由冰川的流速场和流动系数A决定，而A由冰川温度场（T）计算获得：

而冰川温度场（T）可由热传导扩散方程计算得到：

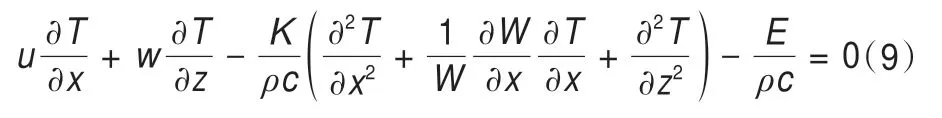
式中：K是热传导系数；ρ是冰川冰密度；c是冰的热容量；w是垂向速度；E是冰体内部的形变热。

该模型的优势在于沿冰川流动方向考虑纵向应力梯度，可以模拟地形起伏。同时在横剖面对侧向拉力进行参数化，考虑了山体对冰川的阻力影响。此外，还考虑了热力耦合模拟，可以获得冰川内部的热学特征。相比三维模型，所需输入数据较少，适用于山地冰川的模拟。与其他动力学模型同样面临的困难在于，一些关键数据和参数化方案对于冰川动力过程十分重要，但很难观测获取，例如冰川底部运动速度、冰川底部温度及含水量组成等。利用该模型研究了珠穆朗玛峰的东绒布冰川的温度和速度分布［25］，以及祁连山老虎沟12号冰川的热力特征等工作［63］。此外，冷伟等［69］发展的三维Full-Stokes模式对格陵兰冰盖的模拟也取得了很好的结果。这些都极大促进了国内冰川流动模型的进一步应用和发展。

整体而言，冰川动力学研究需把流体力学和数值分析方法应用到冰川变化中，计算过程复杂，目前还不能达到普适的应用阶段。与发达国家相比，我国冰川动力学的研究相对薄弱，尚未参与国际冰盖和冰川模型比较计划。从学科发展的趋势和提高冰川学理论角度，国内对冰川的流动模型研究亟需加强，以满足冰川变化预测研究的需求。

4 冰川变化预测研究进展

从冰川变化的理论角度，若由式（2）获得冰川的物质平衡，由式（4）和（5）获得冰川的运动速度，代入式（1），就可研究冰川的演化趋势。但在实际应用中，由于气候变化的不确定性和冰川变化过程的复杂性，对未来气候情景下山地冰川的演化趋势，仍存在较大的不确定性。例如IPCC第五次评估报告显示在RCP2.6～RCP8.5情景下，至21世纪末全球不同规模山地冰川的消融量在15%～85%之间［70］，而最新IPCC第六次评估报告认为30%～80%的山地冰川将消融殆尽［1］。由此可见，对于冰川预测存在较大的不确定性。

在全球尺度上，2006年Raper等［71］首次利用度日模型模拟了全球1°×1°网格内的冰川物质平衡梯度，预估了21世纪全球冰川物质亏损及其对海平面的贡献。Hock等［48］等利用温度指数模型重建了1961—2004年全球冰川年时间尺度的物质平衡序列，以评估冰川在该时间段内对海平面上升的贡献。Kraaijenbrink等［13］采用Huss模型的方法预估了全球气温较工业革命前上升1.5℃对亚洲高山区冰川变化的影响。Huss和Hock［8］预估了全球尺度下冰川变化对冰川区径流的影响，并预估了对不同冰川区径流峰值出现的时间。综合现有研究看，目前公认有三个模型可以较好地模拟冰川在未来气候情景下的变化，分别由Marzeion等［49］、Radić等［50］和Huss等［51］开发。然而，由式（1）可见，因冰川流动会使物质从积累区向消融区迁移，使冰川对气候的响应具有滞后性。从物质和能量守恒的角度，要模拟和预估冰川的真实变化，必须考虑冰川流动引起的冰川形态变化。虽然在Marzeion模型和Radić模型中，采用“面积-体积-长度”比率法估算了冰川末端的进退，但并未严格考虑冰川厚度随时间的变化，本质上缺乏冰川形态变化对冰川流动的反馈机制。相比较，Huss模型虽然由质量守恒角度对冰川每个高程带的厚度和面积变化进行了参数化处理［72］，但由于设定的参数众多，且部分参数物理机制不明确，造成大范围的应用存在较大的不确定性。Clarke等［73］基于“浅冰近似（SIA）”理论，提出了一套考虑三维冰流过程的模拟框架，但地形等边界输入条件要求过高，模型初始化比较困难，普适性并不理想。Zekollari等［74］在Huss等［51］开发的GloGEM模型的基础上，增加了冰流模型模拟冰川动力过程，来模拟欧洲阿尔卑斯山冰川对未来气候变化的响应。Rounce等［75］开发了PyGEM模型来模拟预估21世纪冰川径流的变化。虽然上述模型可以实现对全球尺度冰川变化的模拟，但由于模型之间的物理基础和参数化有较大的差别，造成不同模型的预测结果不尽相同。为促进冰川模型的发展和减小冰川变化预测的不确定性，Hock等［76］于2015年发起了“冰川模型比较计划（Glacier Model Intercomparison Project，简称GlacierMIP）”，截至2022年已进行到了第三阶段（GlacierMIP3）。

冰川厚度作为冰川形态的关键参数，是冰川动力学数值模拟的重要输入参数，但获取大范围的冰川厚度存在较大困难，通常采取参数化或反演方案估算冰川的厚度。为比较不同冰川厚度反演模型的精准度和减小不确定性，Farinotti［77］2017年发起了“冰厚反演模型比较计划（Ice Thickness Models Intercomparison eXperiment，简称ITMIX）”，2020年业已推行到第二阶段（ITMIX2）。

国内早在2001年施雅风先生使用经验统计方法预估在气候变暖情景下，祁连山北麓河地区小冰川将迅速衰退，流域内1 km2左右的小冰川将会在近二三十年大量消亡［78］。但国内对亚洲高山区冰川整体变化预测的研究较为缺乏，且现有缺乏物理基础的模型在数值模拟与预测方面还存在较大的不确定性。除了模型自身的不确定性外，驱动数据的质量和可靠性对于模拟结果有着直接的影响。特别高海拔地区的观测非常有限。对高分辨率、适应性好的ERA5等再分析资料和CMIP5等预估数据进行降尺度，驱动物质平衡和冰川流动模型是最行之有效的手段［51］。国际上，近年来已经在努力开展这方面的研究［75，79］，国内类似研究还比较欠缺。特别是对流域尺度冰川的数值模拟与预测是国内工作的难点［20］，使用再分析资料是一个很好的出口。此外，比CMIP5考虑物理机理更加完善的CMIP6数据的发布，对于山地冰川未来变化的准确预估也提供了新的契机。

5 研究展望

冰川变化是一个极其复杂的过程，冰川数值模拟则是对该复杂过程的高度概化。基于当前国内外的研究现状，以及未来的学科发展趋势，可以看出发达国家对冰川的研究已经完全数值化，从冰川物理角度全方位进行数值模拟，使冰川学研究上升到一个新的理论高度，相关研究在冰川变化、冰川水资源和海平面上升方面有重大的应用价值。与其相比，我国在山地冰川模型的应用和建模方面开展了初步的探索工作，总体上还处于模型的应用或者使用大型计算软件（如COMSOL、Elmer/Ice）对冰川进行数值模拟。这些方法的局限性很明显：①仅能对单个冰川进行模拟；②与其他模式或者模块耦合的可能性很小。因此，山地冰川的数值模拟研究必须加强。为此，提出以下展望：

（1）度日模型存在较大的空间异质性，且不能够解释冰川变化的物理机制和过程，引入能量物质平衡，特别是耦合多层过程的能量平衡过程并考虑全地形影响的模型，对于亚洲高山区冰川物质平衡过程至关重要。

（2）亚洲高山区山地冰川规模远小于极地冰盖，基于冰川变化的物理基础，“浅冰近似原理”并不适用于山地冰川。因此，高阶Stokes方程的求解是山地冰川模型建立的首选。

（3）明确对山地冰川未来变化趋势做出准确预测，是我们长期的战略任务和目标。通过耦合分布式物质能量平衡模型和冰川流动模型，对冰川进行全物理过程的数值模拟，才能深刻探讨冰川变化对气候的响应机理并预测冰川的未来变化，同时推动中国冰川学研究向数值化方向发展。

（4）在气候情景下，流域尺度或区域尺度冰川数值模拟研究是目前工作的重点和急需突破的方向。在现有冰川编目、冰川观测的基础上，如何将分布式物质平衡模型和简化的动力学模式结合，预测和评估未来冰川变化的可能状态及其对冰川水资源的影响，为政府决策、国际气候谈判提供科学数据。在冰川变化数值模拟方面做出一流的研究成果，逐步确立我国在该研究领域的国际领先地位。

（5）冰川数值模拟的门槛相对较高，造成当前国内进行冰川数值模拟工作的科研人员极其不足。从业者不仅要具备冰川变化的基本知识，还需具备深厚的数学和物理知识，特别是流体力学、计算数学和编程方面的知识。对此，一方面要加强研究生的数学和物理知识，另一方要有组织地进行数值模式的研发。