梅里雪山1991年和2019年雪崩事件重建及影响因素分析

段仕美，刘时银，朱钰，缪文飞，韩丰泽，祁苗苗

（1.云南大学国际河流与生态安全研究院，云南 昆明 650500；2.云南省国际河流与跨境生态安全重点实验室，云南 昆明 650500）

0 引言

雪崩是山坡积雪内部的内聚力小于所受重力，底部摩擦力小于剪切应力，使其失稳下滑并引发大量雪体崩落的现象［1-2］。近些年来，随着社会经济发展和工程建设增多，以及登山、科考、旅游活动涉及的范围不断扩大，人类活动受到雪崩危害的风险增加［3］。据统计，1950年以来，奥地利已有1 600多人死于雪崩，平均每年约有30人死亡［4］。对美国科罗拉多州雪崩数据库进行分析可知，有65%的人因雪崩窒息而死［5］。2012年4月8日，巴基斯坦北部锡亚琴冰川地区的一场大规模雪崩将一整座军营全部淹没，直接导致139人死亡［6］。郝建盛等［7］收集了2009—2019年间亚洲高山区的雪崩灾害数据，统计发现该时段总计伤亡1 580人，并发现每年的2月和3月是雪崩灾害频发期。

作为雪崩形成的必要物质基础，积雪容易受其自身物理理化性质和外界自然条件的影响，其与地形、气象条件之间相互作用便会导致雪崩的形成［8］。不同雪崩类型主要取决于积雪地层、土壤特征、气象条件以及外部触发因素［9］。Atwater［10］提出了影响雪崩形成的10个气象及雪层因子。目前将雪崩形成的影响因素概括为三类，第一类是静态地形因素，如坡度、坡向等；第二类是积雪本身的物理性质，如密度、抗剪强度等；第三类是外界自然条件，如降雪、降水、地震等。

雪崩过程由于其突发性及过程复杂，进行直接观测存在较大困难。已有研究提出了一些经验模型或简化的物理模型［11］。此类模型主要针对雪崩运动和破坏参数进行计算（如速度、雪崩流高度、抛程、冲击力、雪崩体积等），从而重建雪崩过程。针对1951年和1954年瑞士阿尔卑斯山发生的特大型雪崩灾难事件，Voellmy［12］根据流体动力学定律重建了此次雪崩的动力学过程，开发了一个雪崩物理模型——Voellmy。Salm等［13］于1966年对Voellmy模型进行了改进，引入了内摩擦和主动与被动流动条件。改进后的Voellmy-Salm（简称VS）模型成为现今大部分雪崩模型的研发基础。基于此，瑞士联邦冰雪和雪崩研究所根据瑞士大量雪崩和泥石流事件的历史数据，开发了二维雪崩动态数值模型——RAMMS（Rapid Mass Movement System）。该模型利用Voellmy-Salm连续介质流模型处理雪崩流体的流变问题，并耦合随机动能（Random Kinetic Energy，RKE）模型，从而能更好地分析雪崩运动过程中特征参数的动态变化。RAMMS模型通过计算两个方向的速度矢量，确定三维地形中雪崩的流动方向和宽度［14］。由于其包含RKE模型和VS模型的特征，可准确预测多种地形条件中雪崩体的运动距离、流速和冲击压力及崩塌体沉积的空间分布等，该模型在雪崩重建和危险评估研究中得到了方法应用［15］。

自1990年代后期以来，针对季风海洋性气候区雪崩的观测和研究几乎空白，对雪崩过程的重建认识不够。梅里雪山是雪崩多发区，1991年1月3日造成中日联合登山队17名队员遇难的雪崩灾害事件影响极大［16-17］。2019年2月16日，我们的野外观测设备记录到梅里雪山明永冰川附近发生了一次规模较大的雪崩，雪崩产生的气浪破坏了架设在明永冰川末端的气象站，雪崩体经过之处林木尽毁，使周围的生态遭受了严重的破坏（图1）。迄今为止，并没有公开发表的文献对上述雪崩过程进行详细研究。尽管国家已明令禁止攀登梅里雪山，但随着气候变暖导致的冰川退缩和雪线上升，以及高海拔研究的推进、人类活动不断向山区的深入，暴露在雪崩风险之下的可能性仍然存在［18］。通过对历史雪崩事件的定量研究，有助于为未来潜在雪崩危害预警、相关活动规避风险提供支撑［19］。本研究利用RAMMS模型对发生于梅里雪山不同地区的两次雪崩事件进行模拟，获得雪崩过程特征参数，在此基础上分析不同类型雪崩的特征。为梅里雪山雪崩预测预警提供基础支撑。通过对梅里雪山两次不同类型的雪崩事件的模拟和重建，对比分析低纬度高海拔季风地区雪崩类型及特征，探讨不同气候条件、不同类型雪崩活动机理。在明确雪崩风险等级的基础上，叠加气候过程以进一步做雪崩预测预警。

图1 2019年雪崩事件现场拍摄的照片Fig.1 Photo taken at the scene of the 2019 avalanche event：avalanche accumulation area（a）；meteorological station damaged by avalanche（b）；trees damaged by avalanche（c）

1 研究区概况

梅里雪山（98°30′～98°46′E，28°10′～28°41′N）位于云南省德钦县，怒江与澜沧江流域界山之一（图2）。受山地地形和冰川运动、融水的侵蚀、搬运、堆积作用的影响，该区冰蚀地貌和冰碛地貌明显。海拔5 000 m以上区域冰川及冰蚀洼地分布较广，冰川粒雪盆常年被积雪覆盖，雪崩和风吹雪广泛。海拔3 500～4 800 m发育有大量的雪蚀洼地，坡度在25°～50°范围内，为雪崩的形成提供了良好的地形条件。梅里雪山主要受西南季风和西风环流的影响，夏季来自印度洋的西南季风暖湿气流从三江谷地向东和向北运动，为本区带来充沛的降水；东春季节由大西洋东进的西风带急流波动在本区上空形成高空槽，带来持续的阴雨天气。若高空槽与南下冷空气形成的冷锋叠加，还会形成较大的降水，为雪崩提供充沛的物质基础［20］。据毗邻的德钦气象站监测资料（1991—2019年），梅里雪山地区年平均气温5.5℃，年平均降水量600 mm。

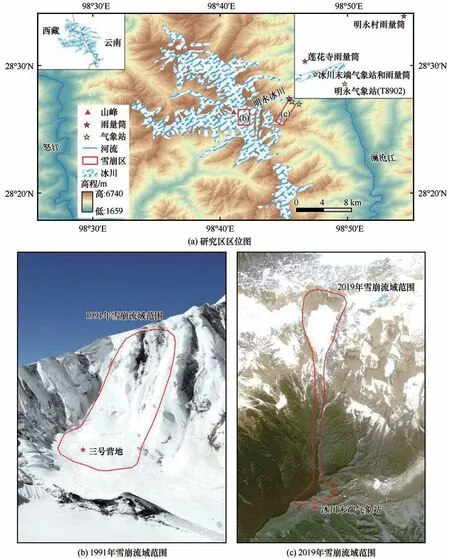
图2 研究区区位图、1991年和2019年雪崩流域范围Fig.2 Study area（a）；avalanche area in 1991（b）；avalanche area in 2019（c）

复杂的地形和丰富的降水造就了本区“有利的”雪崩孕灾环境，导致雪崩活动特征依海拔表现出区域差异。以雪线（海拔5 000 m）为界，雪线以上的雪崩多发育于刃脊或者角峰雪檐，崩塌体多分布于地势平坦的冰川粒雪盆和冰斗地区，以1991年雪崩事件为典型；雪线以下、中海拔地区（海拔3 500～4 800 m）的雪蚀洼地为季节性雪崩源区，运动区为沟槽，堆积区位于冰川山谷和U型谷，是雪崩及其运动裹挟土石树枝碎屑物堆积的区域，常呈扇形，以2019年雪崩事件最为典型。两次雪崩事件的地形特征参数如表1所示。

表1 两次雪崩事件地形特征参数Table 1 Topographic characteristic parameters of two avalanche event

2 数据与方法

2.1 数据

2.1.1 数字高程模型（DEM）

地形要素表征雪崩区的地形特点，需要准确反映雪崩区的地形特征［21］。在RAMMS模型中，一般通过输入地形图或数字高程模型（DEM）来表示雪崩区的地形要素。而DEM的分辨率对模型模拟效果有很大的影响。Buehler［22］等通过比较不同分辨率的DEM对同一雪崩事件的模拟结果来评估DEM质量和分辨率的敏感性，发现25 m的空间分辨率足够准确地模拟大规模雪崩。模拟的流动路径、传输距离、堆积量、运动速度和冲击压力等与2 m DEM模拟以及实地观测结果吻合良好。5 m以内DEM分辨率对模拟结果影响不大，因积雪积累过程通过填充洼地而使小尺度地形变得平滑［23］。本研究使用ALOS PALSAR 12.5 m DEM作为模型输入数据，重建两次雪崩事件，保证模拟结果的准确性。

另外，RAMMS模型模拟需要输入雪崩释放区几何模型，而潜在雪崩释放区与地形坡度密切相关。当坡度小于28°时几乎不会发生大型雪崩，而当坡度大于60°时，因地形陡峭、积雪堆积困难，也无法形成大型雪崩［15］。因此，一般将潜在雪崩释放区的坡度定义为28°～60°之间。在本研究中利用地形表面分析自动识别坡度适合区，并叠加Google Earth影像和野外实地调查数据确定雪崩释放区。

2.1.2 气温降水数据

由于研究区属于高山峡谷地区，交通不便，自然地理环境恶劣，因此缺乏实时监测的气象站点，而相对靠近梅里雪山地区的德钦站气象站，其海拔3 300 m，比研究区冰川末端海拔高，而且该站点气象数据不能直观反映高海拔地区的气象状况。因此本研究主要使用ERA5-Land数据产品进行研究区雪崩气候特征分析。ERA5-Land是欧洲天气预报中心（ECMWF）哥白尼气候变化服务计划的成果之一，该数据产品是在上一代的基础上研发的新一代再分析数据，数据质量更高。已被广泛应用于各种气候分析与研究。与上一代数据相比，具有更高的空间分辨率（0.1°×0.1°），时间分辨率为1 h。利用站点数据校正之后，提取1991年和2019年雪崩事件前后的气温和降水［24］，分析雪崩前后的气候特征，了解雪崩触发的气候背景。本研究使用的ERA5-Land数据产品下载地址为（https：//cds.climate.copernicus.eu/#！/search？text=ERA5&type=dataset）。

2.2 RAMMS重建雪崩过程的原理

本文采用RAMMS-AVALANCHE模型模拟复杂地形中雪崩的流动，其核心是数值求解颗粒运动方程，模拟雪崩流平均深度。该模型可以利用数字高程模型（DEM）计算任意区域、任意时刻的致密雪崩流断面高度、流速、流量及其沿程变化。摩擦力是坡面对雪崩层的阻力。模型使用笛卡尔坐标系：平面坐标X、Y和高程Z，t为雪崩运动时间。雪崩流在任何高度和速度下都是非恒定、非均匀运动的。其运动特征由两个主要参数表示：雪崩流高度h(x，y，t)（m）和运动速度u(x，y，t)（m·s-1），关系式如下：

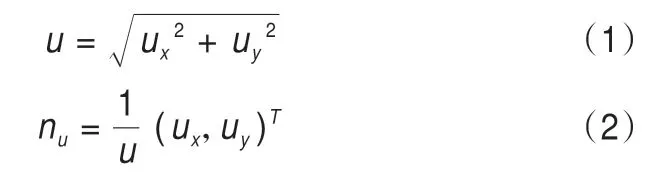
式中：ux为u沿X轴的流速分量；uy为u沿Y轴的流速分量；T为平均流速矩阵的转置；单位向量nu表示雪崩流运动的方向。

摩擦阻力由μ和ξ两个参数共同控制：干摩擦系数μ：基底摩擦（库伦摩擦力），与正应力N有关，通常表示为内部剪切角的正切值；湍流系数ξ：内部摩擦（黏滞摩擦力），与速度的平方u2有关。摩擦阻力S（Pa）的计算公式为：

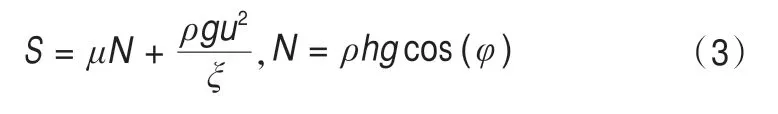
式中：ρ为密度；g是重力加速度；φ是内摩擦角。由上述公式可推出Voellmy流变公式为：

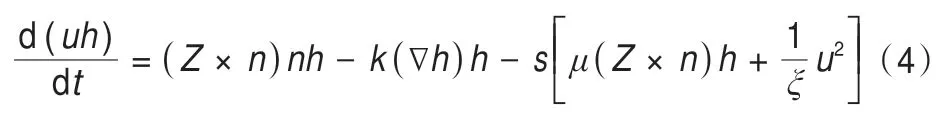
式中：k为压力系数；

2.3 雪崩断裂深度的确定

断裂深度（Release depth）是指雪崩释放区的平均积雪厚度，垂直于坡面测量。断裂深度和坡度密切相关。根据山坡积雪体的平衡条件，山坡上积雪所受重力可分解为平行于山坡的应力和垂直于山坡的正压力，而下滑力（平行于坡面的分力与剪切力之和）及其产生的变形则会使雪层失稳，从而暴发雪崩。由此得到山坡上积雪层临界（极限）厚度hk如式（5）所示［1］。当山坡积雪厚度达到临界厚度hk时，雪层的下滑力与其阻抗力处于平衡状态，这时积雪厚度的增大或雪的力学强度的降低，都会引起雪的滑塌。在本研究中我们讨论雪崩量最大的情况（即山坡积雪全层断裂），认为临界厚度就等于断裂深度。

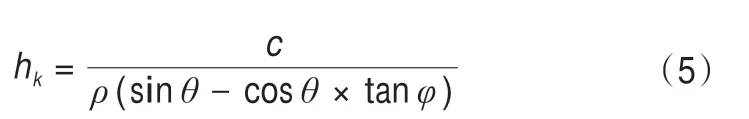
式中：c为雪体与坡面之间的内聚力（g·cm-2）；ρ为雪的密度（g·cm-3）；θ为山坡坡度角（°）；φ为雪与坡面之间的内摩擦角（°），tanφ为内摩擦系数。

由公式（5）可知，内聚力、积雪密度、山坡坡度和内摩擦系数是决定山坡积雪稳定性的关键因素。山坡坡度通过地形分析得到：1991年雪崩源区平均坡度为42°，2019年雪崩源区平均坡度为28°；而积雪内聚力、积雪密度和内摩擦系数主要取决于山坡积雪性质和雪气候条件，其对雪崩的形成发挥着重要作用。早在1979年，王彦龙［1］以天山雪崩站为观测站点测量积雪的这些物理性质。在大约同时期，国外学者Martinelli［25］在南美洲科罗拉多山脉进行人工雪崩爆破实验，以测量雪崩发生时积雪的各种物理属性，得到不同类型的雪（Initial hard slab，Typical aged snow，Persistent soft snow）的物理性质（密度、温度、内聚力、剪切应力、内摩擦系数等）。Bartelt等［26］通过雪槽实验模拟雪崩的发生，采用内聚力模型计算不同情景下积雪的内聚力及各项物理属性的变化情况，给出了雪崩模型预测雪崩发生时可能的积雪物理属性取值。在以上研究的基础上，结合梅里雪山的实际情况，本文中模拟的两次雪崩事件中积雪物理性质取值如表2所示。

表2 积雪的物理性质（据Bartelt等［26］，2015）Table 2 Physical properties of snow（from Bartelt et al［26］，2015）

根据以上内容，利用公式（5）计算两次雪崩事件的断裂深度，有

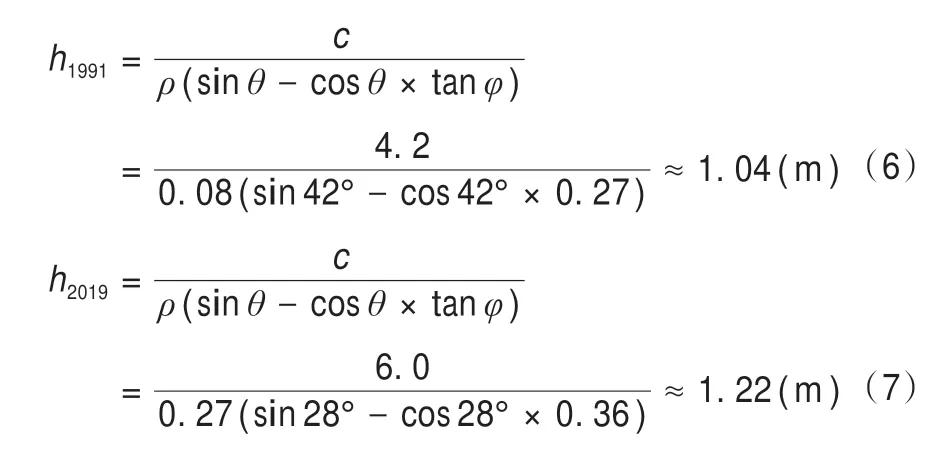
因此得到1991年断裂深度为1.04 m；2019年断裂深度为1.22 m。

2.4 摩擦系数的确定

RAMMS模型有两种摩擦系数设置情景，一种是整个雪崩区（起始区、运动区、堆积区）采用固定的μ和ξ值。固定的摩擦系数值更常用于雪崩区地形特征一致，下垫面相同的雪崩模拟；另一种是“variable”，即μ和ξ值是不固定的，不同的海拔区间（表征不同的地形特征）使用不同的摩擦系数。本研究中的两次雪崩事件属于不同的类型，摩擦系数不同。经过野外调查可知2019年雪崩流经过的区域有沟渠、沟谷和山谷平坦地区，不同的地形条件下摩擦系数不同，因此本次雪崩模拟的摩擦系数需要通过地形特征进行分区取值。通过分析其他雪崩特征并与模型参考值进行匹配以模拟2019年雪崩事件，使用的摩擦系数如表3所示。

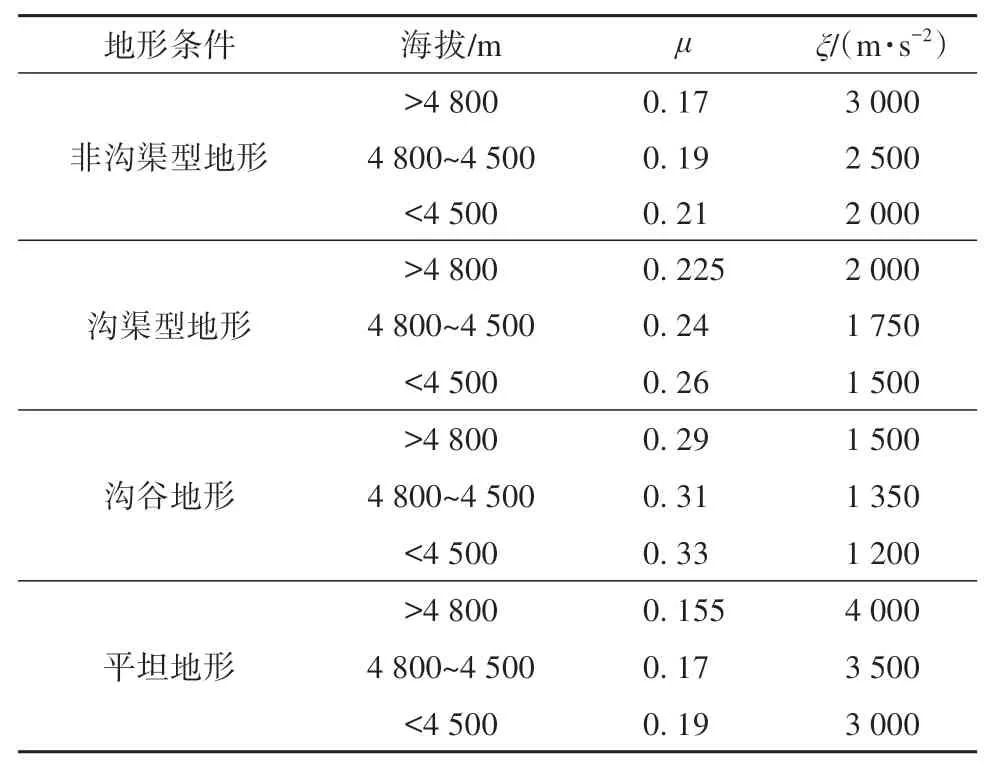
表3 2019年摩擦系数μ和ξ在不同地形、不同海拔下的取值Table 3 Values of friction coefficientsμandξin 2019 at different terrain and altitude

将堆积区范围与野外观测范围进行对比（图3），红线为野外观测的雪崩堆积区范围，栅格为模型模拟出的堆积区范围，将两个范围进行叠加，以分析模型模拟结果的准确性。然后利用“多边形相似度”计算模型模拟堆积区范围与野外观测范围两个多边形的相似度，多边形相似度越高，则表明模拟效果越好［27］。分别计算两个多边形的形状比率相似度、大小相似度、周长相似度、方向相似度以及最终相似度，以评价模拟结果的准确性，计算结果如表4所示。

图3 RAMMS模型模拟的堆积区范围与野外观测范围（红色多边形）对比Fig.3 The RAMMS model simulated the accumulation area and field observation area（red polygon）comparison

表4 相似度计算结果Table 4 Results of similarity calculation

模型模拟结果表明，基于按不同海拔、不同地形进行设置的摩擦系数模拟结果与野外实测基本一致，表明模型手册建议取值的摩擦系数经过海拔调整在本次雪崩过程的模拟中是适用的。同时也说明了只要选取了合适的参数，RAMMS模型可用于梅里雪山地区的雪崩运动过程模拟。

1991年雪崩发生在常年积雪的高海拔地区，无雪崩槽，属于强降雪引发的大规模坡面雪崩。本次雪崩的起始区、运动区和堆积区的下垫面完全一致。因此，在该种情况下，更适合使用固定的摩擦系数来进行模拟。Buser等［28］为了计算固定取值下摩擦系数μ和ξ的最适合大小，通过对1915—1916年，1967—1968年，1974—1975年和1977—1978年内发生的雪崩事件的长时间野外观测以及现场实验，确定了极端情况（新降雪雪崩、松软的雪板雪崩）下最适合的摩擦系数取值。通过试验发现在极端情况下摩擦系数最合适的取值为μ=0.16，ξ=1 360 m·s-2。Schaerer等［29］对常年积雪区形成的雪崩（无岩石和树木参与）的运动速度进行现场观测，通过计算发现此种类型的雪崩的摩擦系数ξ取值范围为1 000～1 800 m·s-2。通过安装在雪崩轨迹上的压力传感器产生的信号证实了ξ取值范围的正确性。因此，本研究中在模拟1991年雪崩事件时采用的摩擦系数为μ=0.16，ξ=1 360 m·s-2。

3 研究结果

3.1 数值模拟结果

图4所示为模型模拟出的梅里雪山1991年和2019年雪崩事件，并给出了各项参数模拟的数值结果（表5），由于两次事件属于不同的类型，且触发因素和发生地区不同，因此各项模拟结果存在很大的差异。相比于2019年较大高差的沟槽型雪崩，1991年坡面雪崩持续时间相对较长。原因与海拔高差有关，2019年雪崩事件启动区与堆积区海拔差较大，崩塌体近似自由落体运动。而1991年雪崩启动区与堆积区海拔差较小，且无雪崩槽，崩塌体只能沿坡面向下滑动。从最后的沉积量上看，两次事件量级都大于6×104m3，都属于大规模雪崩，雪崩最后的堆积量都很大。不同的数值模拟结果表明不同雪崩类型的特点，由此可看出梅里雪山不同地区不同类型雪崩的性质。

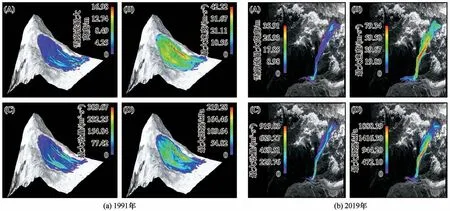
图4 两次雪崩事件模拟结果图：雪崩流最大高度（A）；最大速度（B）；最大压强（C）；最大动量（D）Fig.4 Simulation results of two avalanche events：max flow height（A）；max velocity（B）；max pressure（C）；max momentum（D）［1991（a）；2019（b）］

表5 两次事件数值模拟结果Table 5 Numerical simulation results of two events

3.2 1991年雪崩事件危害分析

图5（a）显示的是1991年雪崩事件的数值模拟结果。表明，雪崩体从海拔5 730 m处启动，沿坡面崩塌而下并堆积在海拔约5 000 m冰川粒雪盆平坦区，形成面积为0.6 km2，体积约67×104m3的堆积体。堆积体平均高度为2 m，最大高度可达13.46 m，依据地形分布成中间高、四周低的椎状堆积体。根据历史资料记录，1991年中日联合登山队的三号营地位于海拔5 100 m的中间位置，处于崩塌体下方，属雪崩堆积区局部厚层积雪区，厚层积雪的压力，强大的冲击力是导致中日联合登山队17名队员全部遇难的主要原因。

图5（b）为三号营地所在截面的积雪层厚度分布图。由图可知该截面最大沉积高度为10 m，最小为1 m。整个截面积雪堆积厚度呈现出依地形变化而变化的特点，地势低的地方厚度大。图5（c）为三号营地所在点整个雪崩过程中积雪堆积厚度随时间的变化曲线，由图可知在约2 min内积雪堆积厚度达到最大，约为10 m。

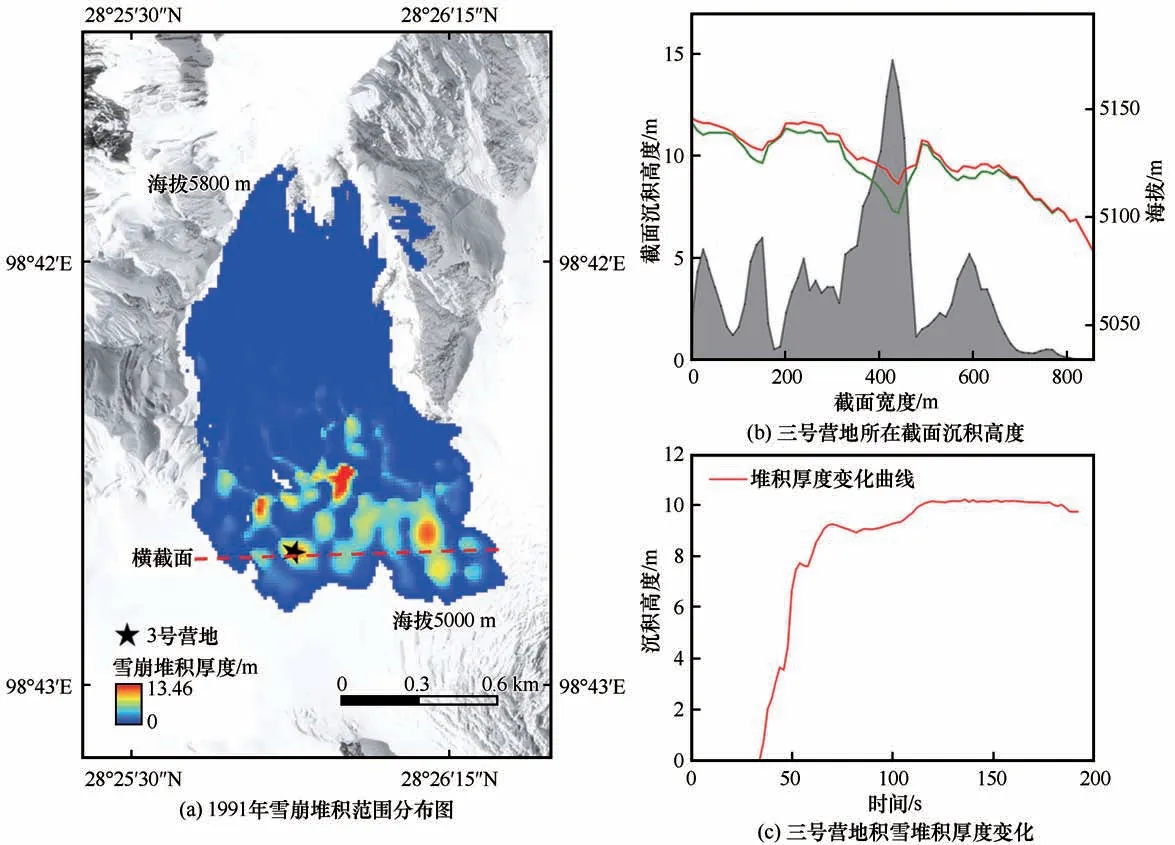
图5 1991年雪崩堆积范围分布图（a）；三号营地所在截面沉积高度［图5（a）中红色虚线］（红色线条为该截面流量变化轮廓曲线，绿色线条为截面地形线，灰色填充区域为该截面积雪堆积厚度变化）（b）；三号营地积雪堆积厚度变化（c）Fig.5 Distribution of avalanche accumulation area in 1991（a）；the thickness of the section at Camp 3［dotted red line in Fig.5（a）］（The red line is the contour curve of flow change，the green line is the terrain line，and the gray filled area is the change of snow accumulation thickness）（b）；changes in sediment thickness at Camp 3（c）

4 讨论

4.1 两次事件影响因素分析

雪崩的暴发强烈依赖气象条件的变化，在本文中利用ERA5-Land数据进行研究区两次雪崩事件前后的气候特征分析。两次雪崩暴发的日期分别是1991年1月和2019年2月，因此分别对两次雪崩地点（1990年：海拔5 500～6 000 m；2019年：海拔4 500～5 000 m）、不同时间段（1990年10月—1991年4月、2018年10月—2019年4月）的气温降水数据进行分析，以分析雪崩发生的气候影响因素。

图6（a）为1991年雪崩发生前后的气温降水变化曲线图，由图可知1990年10月上旬气温高于0℃，最高气温为5℃，此段时间的降水量多，平均每天有7 mm的降水量。进入10月下旬，气温波动下降，但始终低于0℃，这为雪崩的形成提供了良好的冷储条件。进入12月，气温急剧降低，最低气温-19℃，但持续8天之后气温回升，然后一直在-10℃之 间 波 动。1991年1月1日，气 温 骤降（-18℃），降雨量突然增加（19 mm），而后1月3日雪崩发生。图6（b）为2019年雪崩发生前后的气温降水变化曲线图，和1991年相比，2019年雪季开始的晚。2018年11月气温才开始下降（低于0℃），此后温度始终在0℃以下波动，最冷的时候2019年1月最低气温-17℃，这段时间日均降水量约为5 mm，而进入2月份之后，气温快速升高（升高了约6℃），但始终低于0℃，降水量也有所增加（日均降水量10 mm），直到2月16日雪崩发生。

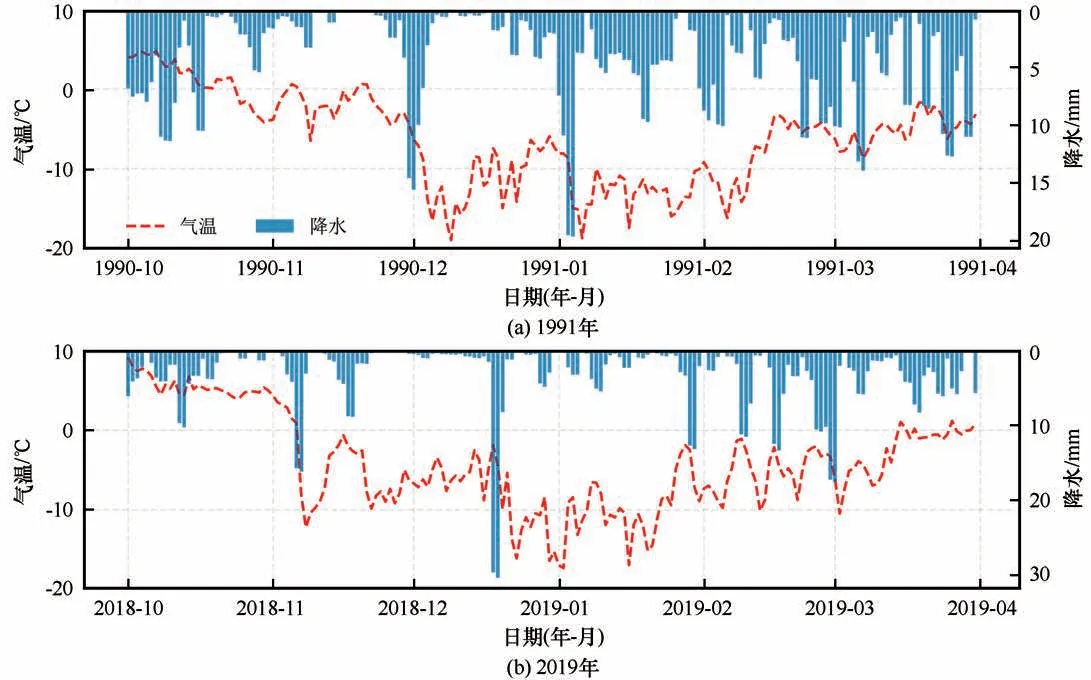
图6 1991年和2019年雪崩前后气温和降水分布Fig.6 Pre-and post-avalanche temperature and precipitation maps：1991（a）；2019（b）

4.1.1 降雪量对雪崩的影响

积雪是同时具有弹性和塑性特征的特殊物质，其物理性质（如粒径、温度和含水量等）决定其弹、塑性的强度。除抵抗塑形形变的韧性外，积雪还具有抵抗弹性形变的刚度。当降雪强度很大（应变率＞10-3·s-1）时，积雪的脆性特征更加明显；而当应变率＜10-5·s-1时，积雪具有更强的延展性和粘弹性，通常认定为一种介于固液之间的材料［30］。其中降雪强度通过影响雪层之间的应变率，进而影响积雪强度。新降雪强度（内聚力）很弱，与其他雪层相比密度明显偏小，其与下层的雪晶连接尚未建立，因此稳定度较差。1991年1月2日夜里10点半（雪崩发生前），三号营地向大本营最后一次通报：“雪下的太大了，帐篷都快被埋了，积雪厚度达1.2 m，队员们每隔几个小时就要出去扫一次雪。”由此表明连续强降雪是触发1991年大规模雪崩的直接原因。短期内降水变多、气温升高，导致积雪在沉积过程中未与相邻的雪层胶结，表现为断裂韧性、抗剪能力差的特性。雪崩前异常的气温和降水事件破坏了之前雪层之间稳定的胶结，雪崩日异常增大的降水使原本未能良好胶结的雪层抗压能力下降，雪层破裂，出现坡面雪板雪崩。

4.1.2 气温对雪崩的影响

作为一种特殊的材料，雪的各种力学性质高度依赖于温度的变化［31］。温度是导致雪崩形成的决定性因素，特别是在没有新降雪的情况下，气温波动对雪崩影响明显［32］。气温对积雪稳定性的影响是复杂的，因为气温的变化会以各种方式影响雪的稳定性。同样，气温的变化速度也很重要。风暴期间温度的上升和风暴后不久温度的迅速上升会导致雪层不稳定。雪的力学特性与温度高度相关［33］，McClung和Schweizer［34］综述了温度对雪的硬度、韧性和剪切强度的影响。一般来说，在雪层中存在两组重要的相互竞争的效应：（1）变质（取决于温度、温度梯度和其他雪的性质）和蠕变；（2）力学性质（不包括变质效应），包括雪的硬度、韧性和强度。而第2组效应对雪的稳定性影响显著，即一旦温度发生变化，积雪的力学性质和强度会立即变化，从而导致雪层稳定性降低暴发雪崩。由图6（b）可知雪崩发生前一段时间气温有回升趋势（2019年1月28日），之后又降低到-10℃左右。当温度降低的时候，雪层下部脆弱层趋于稳定；而短暂的升温使雪体刚度变小，雪层强度减小，导致其在塑性变形以及断裂过程中吸收能量的能力增强。升温-降温周期大概持续了两次，在第三次升温时（2月16日）雪崩暴发。由该过程可知气温变化影响了雪层的稳定性，导致雪崩发生。

4.2 雪崩危险性评估与区划

雪崩危险性评估可在一定程度上为雪崩预测提供参考，根据雪崩危险区划图可识别潜在的雪崩高风险地区，日常登山科考等活动尽量避开此类地区，可在一定程度上减少雪崩危害［35］。根据雪崩危险性评估的方法［36］，利用层次分析法（Analytic Hierarchy Process，AHP），结合地形（坡度、坡向、海拔、曲率、地面粗糙度）、气候（气温、降水）和下垫面（土地覆盖类型）［图7（a）］等因素对梅里雪山的雪崩危险性进行区划，得到梅里雪山雪崩极高危险性、高危险性、中等危险性、低危险性和极低危险性五个危险等级，并分区成图［图7（b）］。由图可知，利用层次分析法得出的梅里雪山雪崩极高危险区主要分布在中高海拔区，几条海洋性冰川区属于雪崩低危险区和极低危险区，雪崩中等危险区主要分布在中低海拔地区和较高海拔地区，这些地区要么是因为雪深不够达不到雪崩危险，要么是因为位于高海拔地区坡度较大，无法“孕育”雪崩。而中高海拔的冰川粒雪盆和季节性雪蚀洼地成为梅里雪山雪崩良好的场所。季节性雪蚀洼地分布广泛，所以雪崩中高风险地区整体分布较多。

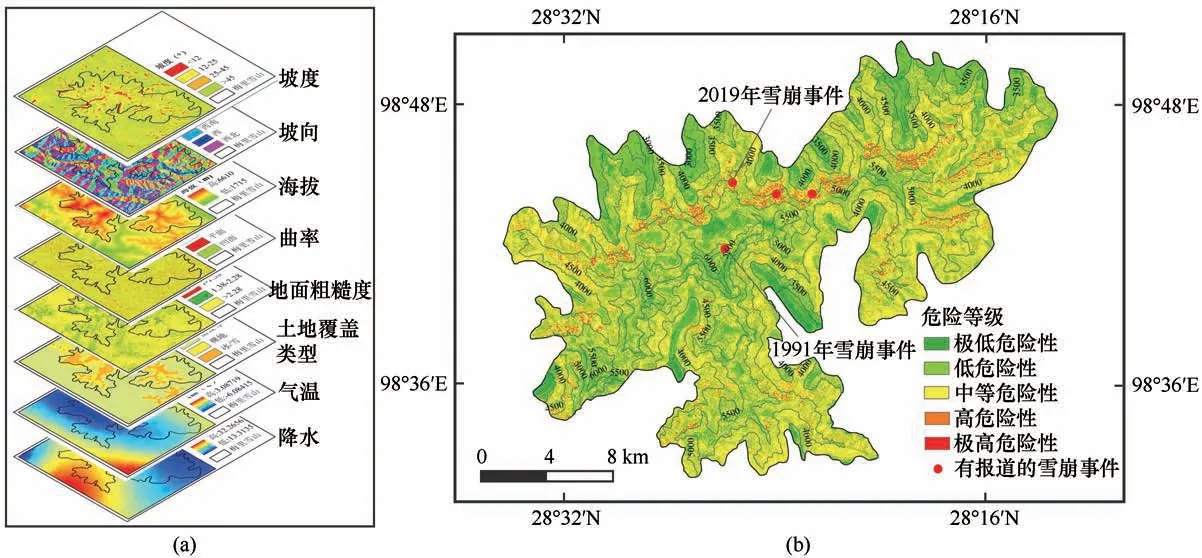
图7 雪崩发生关键影响因子（a）；梅里雪山雪崩风险等级划分图（b）Fig.7 The key influencing factors of avalanche occurrence（a）；map of avalanche risk rating in Meili Snow Mountain（b）

本研究中的两次雪崩事件发生地点正位于雪崩极高易发区和高易发区内。因为雪崩灾害救援的黄金时间只有30 min，因此灾害暴发后的致死率很高，所以做好雪崩的预测预警非常重要。而为了更深入地构建雪崩预测方案，必须结合历史雪崩事件构建架构体系。当确定雪崩高发区后，叠加适当的天气条件（积雪累积量），以RAMMS模型为手段，就可预测出雪崩的堆积区、运行距离、最大速度以及产生的压力等（给出适当的范围）。基于此可以发布雪崩预警信息，防患于未然，减少不必要的损失。应用从基本规律和历史事件中获得的经验中可以得出基础的预防规则［37-38］。因此，重建历史灾害事件可以更好地预防未来灾害的发生。

5 结论及展望

（1）1991年雪崩共持续了192 s，雪崩体从海拔5 730 m处断裂，沿坡面崩塌而下最终堆积在海拔约5 000 m的冰川粒雪盆地区，形成面积为0.6 km2，体积约67×104m3的堆积体；堆积体最大高度为13.46 m，登山队的三号营地被崩塌体完全淹没。数值模拟结果显示雪崩运动过程中雪崩流最大高度和最大速度分别是16.98 m和42.22 m·s-1。

（2）2019年雪崩共持续了158 s，雪崩流最大高度35.91 m，最大速度79.34 m·s-1，堆积量76.2×104m3，雪崩堆积范围与我们野外观测到的一致。

（3）两次雪崩事件模拟结果揭示了梅里雪山地区不同海拔、不同类型雪崩的特征。为雪崩预测预警提供了良好的参考。野外积雪性质、气象条件观测可以确定雪崩的成因和类型，而数值模拟则可以分析和再现雪崩动力学。根据观测的雪崩堆积范围，通过参数率定，数值模型可以给出雪崩路径、堆积量、运动速度等定量结果。在此基础上，结合雪崩灾害危险区划图以及叠加实际的天气过程，可实现定点雪崩灾害的预测，发布预警信息。因此，RAMMS模型能够较好地进行雪崩过程重现和危险性区划，是冰川雪崩灾害建模和预测的有效工具。