年度变化百分比与年均变化百分比在医学研究变化趋势分析中的应用*

海军军医大学卫生勤务学系军队卫生统计学教研室(200433)

秦宇辰 郭 威△

【提 要】 目的 介绍比较医学研究与公共卫生工作中常用的两大变化趋势描述指标，年度变化百分比(annual percent change，APC)和年均变化百分比(average annual percent change，AAPC)间的异同，介绍两者在joinpoint软件中的实现方法，为两者的实践运用提供实用建议。方法 比较分析两个指标的基本原理、方法特性和相对优劣势，论述各指标的适用情景和应用价值。结果 APC的使用需严格遵守线性趋势假定，而AAPC具有诸如无需线性变化趋势假定、适用面广、方便各亚组间变化趋势比较、更充分利用既有信息和取值对分割时间区段内子时间段不敏感等优点，在线性变化趋势假定下可化简为APC。结论 AAPC具有显著的方法学优势，可更科学、有效地刻画观察期内的总体变化趋势，在医学研究的趋势分析中应优先选用。

医学研究与公共卫生工作中，常采用平均增长速度、年度变化百分比(annual percent change，APC)和年均变化百分比(average annual percent change，AAPC)等指标定量分析描述某事物或现象的时间变化趋势。已有研究表明，相较于平均增长速度，APC能更充分利用每个时段观察值的信息，科学性和严谨性更强，推荐在实践工作中优先使用[1]。然而目前，尚未有研究介绍比较年度变化百分比(APC)和年均变化百分比(AAPC)两种时间变化趋势描述指标的特点与相对优劣势。本文旨在简要介绍两个指标的基本原理和特点，比较它们的优劣之处，并介绍软件实现方法，以期为其推广应用提供参考。

指标简介

1.年度变化百分比(APC)

假设目标现象y(如发病率、死亡率等)在整个观察期内的变化速度恒定，采用线性回归方程ln(y)=b0+b1x，拟合时间变量x与目标现象的自然对数值ln(y)之间的线性关系，通过对该直线斜率b1的t检验，实现对APC取值是否为0的假设检验。假设2015-2020年间某疾病发病率的APC为1%，2015年的发病率为20/10万，则2016年的发病率为20/10万×1.01=20.2/10万，2017年的发病率为20/10万×1.0122=20.402/10万，以此类推。APC及其95%置信区间(95% confidence interval，95% CI)的计算公式为：

APC95%CI={exp(b1±s×td(q))-1}×100，q=1-α/2

其中，s表示拟合线性回归方程斜率b1的标准误，td(q)指自由度为d的t分布的第百分之q×100分位数。

2.分段年度变化百分比(sAPC)

当对数化后的发病率或者死亡率随时间呈线性关系时，可用APC描述其变化趋势。而当该线性假定不满足时，观察时间内的非线性变化趋势可采用分段回归模型(segmented regression model or piecewise regression model)[2]，计算分段年度变化百分比sAPC(annual percent change from segmented analysis)进行描述。sAPC的基本思想是，将观察期内的非线性变化趋势划分为多个呈线性变化的子时间段，并分别采用线性模型刻画。具体地，设观察期内有k个“趋势转折点”(trend transitions points)，将整体变化趋势划分为k+1个子时间段。每个子时间段内的变化速率认为不变，而子时间段间的变化速率可以不同。在每个子时间段内分别拟合对数化的目标现象特征和时间的线性回归模型，得到各个子时间段内的sAPC，具体计算方法参见相关文献[3]。sAPC在实际应用中可能存在以下问题：(1)无法用一个数值综合描述一段固定长观察期内(如10年、20年等)的总体变化趋势；(2)在比较不同性别、年龄段等亚组间的变化趋势时，不同亚组的趋势转折点个数及子时间区段不同，导致无法直接使用sAPC进行组间比较。

3.年均变化百分比(AAPC)

鉴于sAPC存在的问题，年均变化百分比AAPC被提出用于综合描述观察时间段内的总体变化趋势，方便不同亚组间的趋势比较。其基本思想为，首先基于分段回归模型得到k+1个子时间段的变化速率bi(i=1，…，k+1)，然后对bi加权求和得到一个综合数值。各个bi对应的权重Wi为各个子时间段长度占总观察期的百分比。

假设某现象对数化后的发生率ln(y)在时间段[a，b]内呈非线性变化，使用分段回归模型拟合后得到k个拐点，也即k+1个变化速率恒定的子时间段，则AAPC及其95%CI的计算公式为：

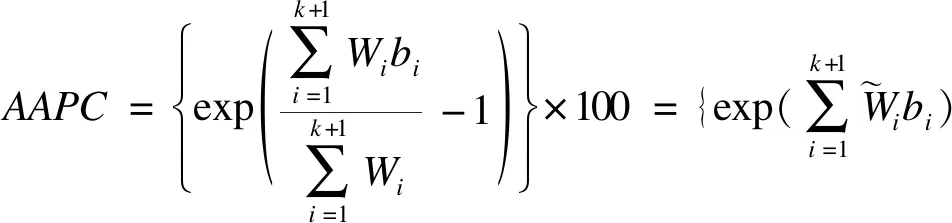
-1}×100

用于两组比较时，可采用下式计算两组AAPC差值AAPC(1)-AAPC(2)的95%CI。其中，AAPC(1)表示组1(如男性人群)在观察时期内的AAPC值，AAPC(2)表示组2(如女性人群)在观察时期内的AAPC值。

4.三类时间变化趋势描述指标相对优劣势及关联

APC、sAPC和AAPC三类时间变化趋势描述指标的相对优劣势如表1所示。基于简单线性回归的APC计算简单，易于理解和解释，但其对线性变化趋势假定的强依赖也客观限制了其适用的问题情境。而基于分段回归模型的sAPC则能很好地解决这一问题，通过引入趋势转折点，将总体的非线性变化趋势切分为若干个呈线性变化趋势的子时间段并分别描述其平均变化百分比，如此即可为整体的非线性变化趋势提供一个细致、全面的多区段变化趋势描述。但sAPC不利于综合把握观察期间的总体变化趋势。此外，由于分段回归模型很可能在不同亚组中拟合出不同的时间转折点和子时间段，故无法使用sAPC进行亚组间变化趋势的检验和比较。AAPC是由各子时间段sAPC加权得到的综合指标，既可描述观察期内的总体变化趋势，也可用于亚组间的趋势比较[6]，其实质是各子时间段的年度变化率的几何均数，故被称为年均变化百分比[3]。值得注意的是，APC可看作AAPC的特例，若整个观察期的变化速率恒定，AAPC可化简为sAPC或APC。由于AAPC对于子时间段的选取不敏感，在描述子时间段变化趋势时，也可利用整个观察期的信息。

总体而言，AAPC相较于传统的APC有以下三点显著优势：(1)AAPC无需线性趋势假定，适用面更广；(2)AAPC可用于亚组间共同观察时间段内的总体趋势比较和检验；(3)当AAPC描述被趋势转折点分割出子时间区段的变化趋势时，任意子时间段内任意两时点间的AAPC都相同(均等于该子时间段的sAPC)，故其对子时间区段内的子区间选取不敏感。计算AAPC需基于分段回归模型，故AAPC描述子时间区段变化趋势时可利用整个观察期的信息。而传统的APC只能使用该子区间的有限数据重新计算变化速率，故会对所选定的子区间比较敏感。综上，在描述观察期内的总体变化趋势时应尽可能选用AAPC，若使用APC则应注意其所需的线性假定是否满足。当我们对观察期内各时点的具体变化趋势感兴趣时，可使用基于分段回归模型的sAPC详细刻画。

表1 三类时间变化趋势描述指标间的优劣势比较

实例应用及软件实现

AAPC和APC可由美国国家癌症研究所开发的Joinpoint软件计算获得[4]。用户只需在官网(https：//surveillance.cancer.gov/joinpoint/)签署使用协议并完成注册便可免费下载安装。该软件分为桌面版和命令行版。桌面版适合习惯进行界面点选操作的用户，命令行版则允许用户编写代码执行批量分析任务。目前软件的最新版本为Join point Regression Program，Version 4.8.0.1(Statistical Research and Applications Branch，National Cancer Institute)。

如下以郑文龙等[5]报告的2006-2015年天津市宫颈癌死亡率数据(表2)为例，介绍如何使用桌面版Join point 4.8.0.1软件计算APC和AAPC。

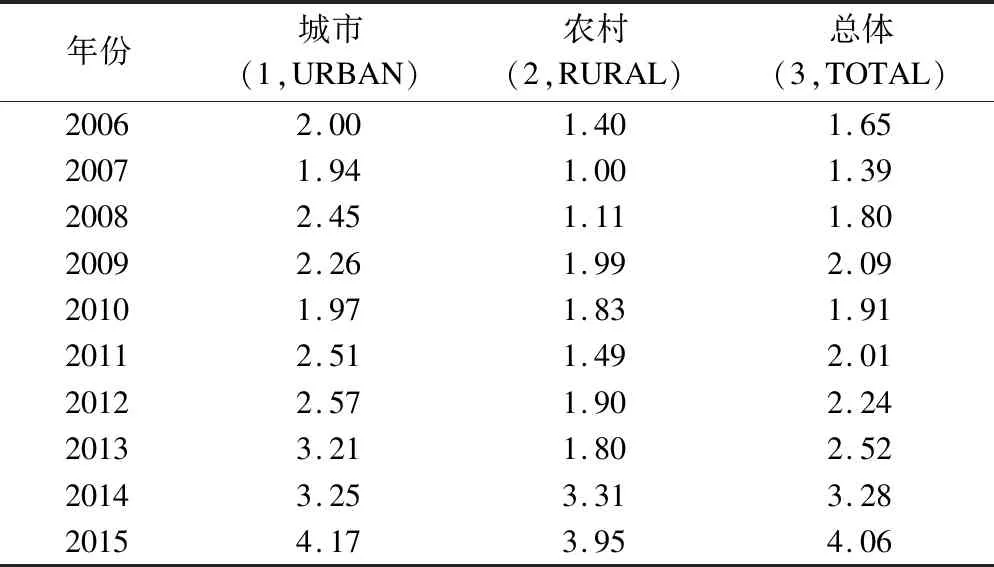
表2 2006-2015年天津市宫颈癌死亡率(/10万)

1.数据整理和导入

首先将表2中数据整理成纵向格式，数据包括year(年份)、mortalityrate(死亡率(/10万))和grp(分组，1：城市，2：农村；3：总体)三个变量，如图1所示。需注意的是，原始数据需按照分组变量grp和时间变量year升序排列后，方可导入Joinpoint软件，否则软件会提示发生错误。

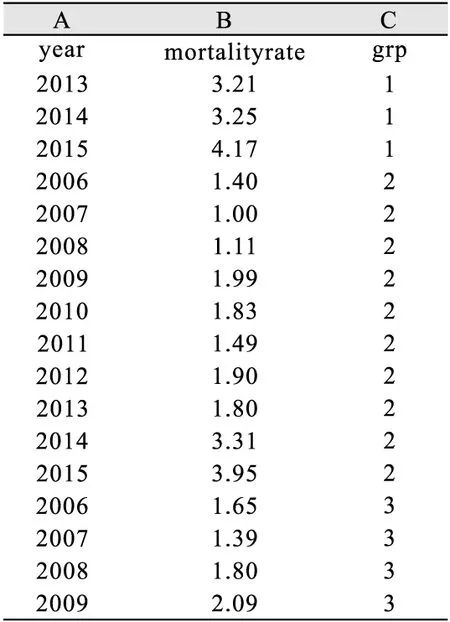
图1 可导入Joinpoint软件数据格式举例

Joinpoint软件支持*.dic(Seer*Stat Dictionary)、*.csv、*.gz、*.txt、*.xls、*.xlsx等多种数据格式导入。打开软件后，在界面菜单栏点选“File”→“New Session”，随后在弹出的界面中，选中目标数据文件并点击“打开”，则可在新建的Joinpoint Session会话框中分别点选界面左上端的“Input File”、“Method and Parameters”和“Advanced Analysis Tools”设置数据导入和分析的参数。

2.软件参数设置

首先在新建的Joinpoint Session会话框中的“Input File”界面(图2)设置数据导入和模型基本参数。界面上半部分的数据导入参数通常保持默认即可，下半部分的模型基本参数设置中，首先需在右侧的“Independent Variable”下拉菜单栏中将时间变量year选入为分段回归模型的自变量；然后，在左侧的“Dependent Variable”栏目的“Type of Variable”下拉菜单中选中“Crude Rate”；设定“Crude Rate”对应的变量为mortalityrate；随后在左侧底端的“Heteroscedastic Errors Option”下拉菜单栏中选中“Constant Variance(Homoscedasticity)”，设定回归模型的随机误差项为同方差的。由于同方差假定在实践中经常无法满足，故当率的标准误可获取时，最好选择“Standard Error(Provided)”并将标准误变量选入“Standard Error”下拉菜单，以允许软件使用加权最小二乘法处理异方差问题。本界面左下方的“Log Transformation”显示，默认会先对原始的死亡率进行自然对数转换后再拟合回归模型。如此即完成了所拟合分段回归模型的基本参数设定，最后在“By Variables”子界面下点击“Add”选项，将分组变量grp纳入模型，允许软件按grp变量分别拟合分段回归模型以分析三组(城市、农村以及总体人群)的死亡率变化趋势。

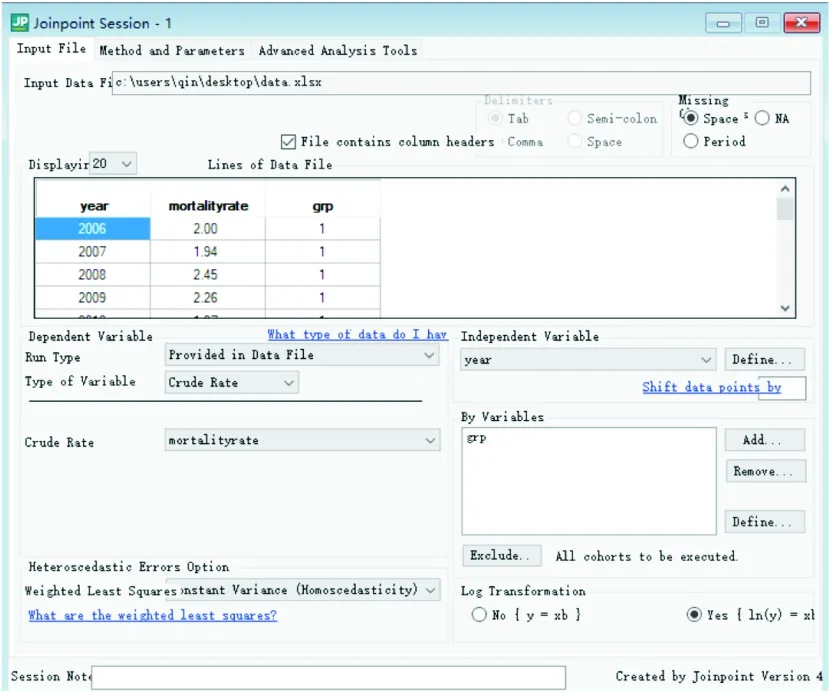
图2 Joinpoint Session会话框的“Input File”界面

在“Method and Parameters”界面可以详细设置分析的方法和参数，一般采用默认设置即可。点选界面左下端的“AAPC Segment Ranges—Entire Range”并设定时间范围即可计算该时段内的AAPC。设置完毕即可点选软件界面上端快捷方式栏中的“Execute Current Session”按钮，运行分析程序获得结果。

3.分析结果

软件结果输出界面如图3所示，左侧菜单栏显示，界面中包含URBAN(城市)、RURAL(农村)和TOTAL(总体)三个队列的分析结果。每个队列均拟合了两个分段回归模型，标★号的为软件推荐的拟合模型，城市组和农村组因十年间的死亡率变化趋势均较为稳定，无明显趋势转折，故软件推荐采用“0 Joinpoints”模型，在总体人群中发现一个有意义的趋势转折点，故软件推荐采用“1 Joinpoints”模型。右侧的“Graph”视图图形化展示了三组死亡率变化趋势的拟合情况，可通过点选结果输出界面左上角的“Filter Cohorts”按钮下的“View Multiple Models Simultaneously”并多选左侧菜单栏显示的多组拟合曲线，使其展示在同一画幅中。在软件菜单栏“Output”—“Options”下可设置结果输出界面各子界面的展示形式，在“Graph”下完善美化趋势图，详细过程此处不赘。

拟合趋势如图3所显示，城市组和农村组2006-2015十年间的死亡率总体变化趋势较为稳定，无明显的趋势转折点，两组APC分别为7.68%和12.74%。而总体人群的死亡率变化趋势于2013年存在一个有意义的转折点，2006-2013年间的APC为7.03%，2013-2015年间的APC为29.94%。

图3 Joinpoint软件的图形化分析结果

图4展示了“Trends”子界面的结果，主要包括各组的APC、AAPC及其95%CI的上下限、检验统计量和P值等详情。可以看出，2006-2015年间，城市、农村和总体人群的宫颈癌死亡率AAPC为7.68%(4.39%，11.07%)、12.74%(5.85%，20.08%)和11.74%(4.40%，19.60%)，P值均小于0.01，提示三组宫颈癌死亡率的年均变化趋势有统计学意义。本实例中，由于城市组和农村组十年间均无有意义的趋势转折点，故此两组AAPC和APC的点估计及95%CI一样。

图4 Joinpoint软件的趋势分析结果

小 结

本文简要介绍了APC、sAPC和AAPC三个指标的基本原理及关联关系，梳理比较了三者的优劣势，给出了使用Joinpoint软件进行基础趋势分析的基本流程和参数设置，以期为医疗和公共卫生研究者提供参考。实际研究中，APC和AAPC均得到较为广泛的应用，但许多文献使用APC时并未充分报告指标所需的线性假设是否满足，可能存在较多方法误用的情况。研究者应重视各个指标背后的前提假定，结合自己的实际问题作出合理选择。鉴于AAPC的显著优势，本文建议在实践工作中优先选用AAPC，如可能，可同时报告APC和AAPC的结果。限于篇幅，本文未介绍如何使用Joinpoint软件进行亚组间变化趋势的检验和比较，我们将另文介绍具体实现方法及注意事项。感兴趣的读者可以在Joinpoint软件官网，下载软件的使用手册研读学习。用户也可在官网上反馈Joinpoint软件使用过程中遇到的问题并寻求指导和帮助。