基于C#与R语言的重复测量设计定性资料统计分析的自动化实现研究*

郭迎暄 陈 达 谭志军 米白冰 黄昌可 廉恒丽△

【提 要】 目的 基于C#语言和R语言开发一款便于临床医生使用的软件，用于实现重复测量设计定性资料统计分析的自动化，确保结果准确、完整和规范，提高科研效率。方法 首先用C#语言将统计分析数据导入到软件中，然后调用R语言命令脚本，完成重复测量设计定性资料的统计分析与结果输出。最后通过实例，验证本自动化实现软件运行的效果。结果 基于C#语言和R语言相结合开发出的统计软件运行结果与SPSS操作结果完全一致，统计分析结果包括了模型选择、模型模拟结果和模拟结果预测三部分。其操作简便，结果自动化呈现，减少了结果判断与模型选择的错误，确保了结果的准确性和规范性。结论 该软件能够自动实现重复测量设计定性资料的统计分析，值得在临床上推广使用。

在临床研究中，常常收集多次重复测量设计的结果变量(因变量)及其影响结果变量的数据(自变量，如性别、年龄、治疗方法、疾病等)。重复测量资料是对同一受试者的同一观察指标在不同时间点上进行多次测量(≥3次)所得的资料，通常用于分析该项观察指标在不同时间点上的变化特点[1]。数据类型可分为定量数据和定性数据，其中，定性数据是指测得的仅反映某一方面性质的指标，并不能用具体的数值表示。定性重复测量资料根据因变量类型可以分为离散型变量、分类变量和等级变量，分析模型可包含固定效应、随机效应或者混合效应。对于临床医生而言，选择正确的模型和统计方法进行数据分析，得出正确的结果和结论，具有一定难度且需要花费很大精力。因此，迫切需要开发一款能够实现定性重复测量数据统计分析自动化的软件。鉴于此，本研究将结合C#语言和R语言进行软件设计和开发，并通过实例展示软件在临床研究中的应用。

软件设计与实现

1.软件设计原理

C#是微软公司推出的一种面向对象的编程语言，具有可视化操作和高效率运行的特点，其支持快速地编写各种基于Microsoft.NET平台的应用程序[2]。R是用于统计分析和统计绘图的语言和操作环境，是一个免费软件，拥有各种各样的R统计分析包，通过这些R语言包，可以进行教育、医疗、可视化、统计学、人工智能等方面应用。

本研究以C#开发平台Microsoft Visual Studio Enter Prise 2019为基础，结合R软件lme4程序包和geepack程序包实现重复测量设计定性资料的统计分析，其中，R软件环境采用R(v.3.6.1)、R studio(1.2.5001)版本。C#对R语言的调用方法有两种，一种是通过R语言的COM接口，直接和R语言进行交互；一种是通过RDotNet.dll与R语言进行交互。本软件通过后者与R语言进行交互，首先，开发环境需要先安装.NET Framework4和R.dll；然后，在C#程序中添加对RDotNet.dll项目的引用；最后，利用REngine对象的方法Evaluate、CreateNumericVector和CreateCharacterMatrix等创建R向量和矩阵，实现C#对R语言函数的调用。基于两种语言的特点，使得开发界面友好、操作简便、自动化运行的统计软件成为可能。

2.软件统计分析流程

软件根据研究目的和研究设计、因变量类型与分布、因变量与自变量关系，选择合适的统计分析方法进行数据分析。不同的统计分析方法涉及的参数不同，对应的界面也会有略微调整。本文用定性资料二分类GEE模型和无序多分类GLMMs模型为实例，来说明软件如何实现数据导入和自动化输出统计分析的结果。统计分析与模型选择流程见图1。

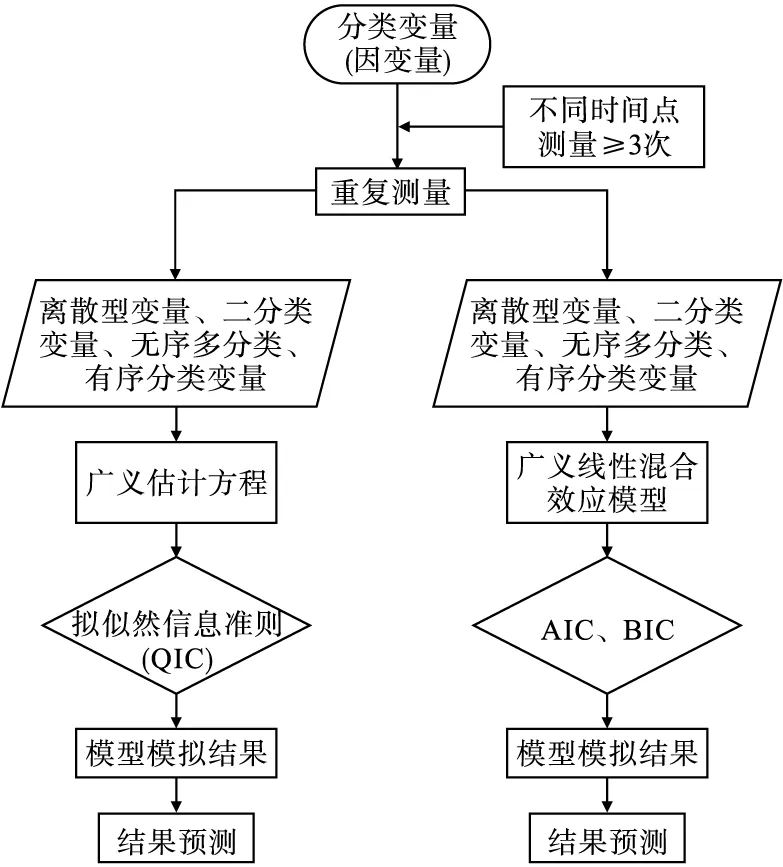
图1 统计分析与模型选择流程图

3.软件界面设计与功能介绍

该软件界面(如图2)左侧红框区为菜单栏，根据不同的资料类型选择适用的统计分析方法。右侧蓝框区为数据导入格式示例区，可进行数据导入。右侧中部绿框区为参数设置区，分别选择因变量和自变量。右侧下方紫框区为结果显示区，根据不同的统计分析方法，显示相应的结果。

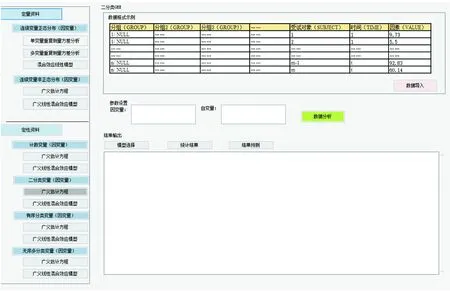
图2 软件界面图

软件验证

为了测试该软件的可靠性与有效性，本文介绍二分类重复测量资料广义估计方程与多分类重复测量资料广义线性混合效应模型在该软件的自动化实现。

1.广义估计方程

广义估计方程(generalized estimating equation，GEE)是Liang和Zeger在广义线性模型和拟似然方法的基础上提出的一种分析纵向数据的方法。GEE可以处理有缺失值的资料，允许每个观察对象的观察次数不同，观察时间间隔亦可不同。广义估计方程应用条件较宽，除了正态分布，可以利用连接函数将高斯分布、二项分布、多项分布、Poisson分布、Gamma分布等多种分布的因变量拟合为相应的统计模型，解决了重复测量数据非独立性问题，可得到稳健的参数，最大程度减少测量数据的有效信息损失。

假设yij为第i个观察对象的第j个观察值(i=1，…，n；j=l，…，p)，Xij(Xij1，Xij2，…，Xijm)为相应的自变量向量。各观察对象是独立的，但同一观察对象内的观察值间存在相关。模型的基本构成如下：

(1)建立yij与各自变量Xij(Xij1，Xij2，…，Xijm)之间的函数关系

E(yij)=uijg(uij)=β0+β1Xij1+β2Xij2+…+βmXijm

(1)

其中g(uij)为联结函数，可根据数据类型选取合适的联结函数。

(2)建立yij的方差与平均值之间的函数关系

Var(yij)=v(uij)·φ

(2)

v(uij)为已知方差函数，φ为尺度参数，表示y的方差不能被v(uij)解释的部分。

(3)对yi=(yi1，…，yip)′选择一个p×p维作业相关矩阵Ri(α)，构造广义估计方程如下：

(3)

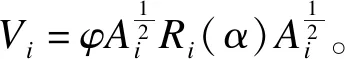
GEE的特点是采用实际计算得到的残差函数，作简单回归从而获得作业相关矩阵。相关矩阵存在多种结构(等相关结构、相邻相关结构、自相关结构、不确定型相关结构、独立相关结构)，模型拟合的好坏可以通过QIC判别准则做出判断[3]。通过QIC大小决定合适的大小相关矩阵，在同一模型中QIC值越小模型越合适[4]。对于GEE算法而言，即使对相关矩阵的结构选择不当，也能得到有关结果变量的回归系数及其方差的一致性估计值[5]。当样本含量较大时，因对作业相关矩阵的选择不当而引起的效率损失可以忽略不计。

(1)背景资料

本研究为一项单中心、前瞻性干预性研究，观察两组不同治疗方案的治疗效果。研究因素为组别，即单纯西医治疗组(90例)和中西医结合治疗组(90例)，分别于治疗后1周、1月、3月共3个时间点观测记录治疗效果。

表1 研究变量说明

(2)R程序代码

#原始excel数据导入

library(readxl)

#数据读取操作

data<- read_excel(file.choose())

data$GROUP<- factor(data$GROUP)

data$TIME<-factor(data$TIME)

data$AGE<-factor(data$AGE)

data$ID<-factor(data$ID)

#模型适配

library(geepack)

fit1<- geeglm(EFFECT ～ GROUP + AGE + TIME，id=ID，data=data，corstr=“ar1”，family=‘binomial’)

fit2<-geeglm(EFFECT ～ GROUP + AGE + TIME，id=ID，data=data，corstr=“exchangeable”，family=‘binomial’)

fit3<- geeglm(EFFECT ～ GROUP + AGE + TIME，id=ID，data=data，corstr=“independence”，family=‘binomial’)

sapply(list(fit1，fit2，fit3)，QIC)

#比较几种模型的QIC值，选择QIC最小值模型进行统计分析与结果输出

coef(summary(fit3))

#编写GEE95%可信区间函数

confint.geeglm<- function(object，parm，level=0.95，…){

cc<- coef(summary(object))

mult<- qnorm((1+level)/2)

citab<- with(as.data.frame(cc)，

cbind(lwr=Estimate-mult*Std.err，

upr=Estimate+mult*Std.err))

rownames(citab)<- rownames(cc)

citab[parm，]

}

confint.geeglm(fit3)

#结果预测

pred=predict.glm(fit3，type=“response”，newdata=data)

predict=ifelse(pred>0.5，1，0)

data$predict=predict

library(vcd)

addmargins(table(data$PREDICTEDVALUE，data$EFFECT))

(3)结果展示与表达

本研究采用广义估计方程研究本案例的二分类重复测量的数据，运算结果如下：

a.模型选择

根据拟似然信息准则(QIC)统计量进行模型选择，结果表明，independence模型QIC值最小，若遇到ra1、exchangeable指标QIC值与independence指标QIC值相同时，以ra1为最优。

b.模型拟合结果

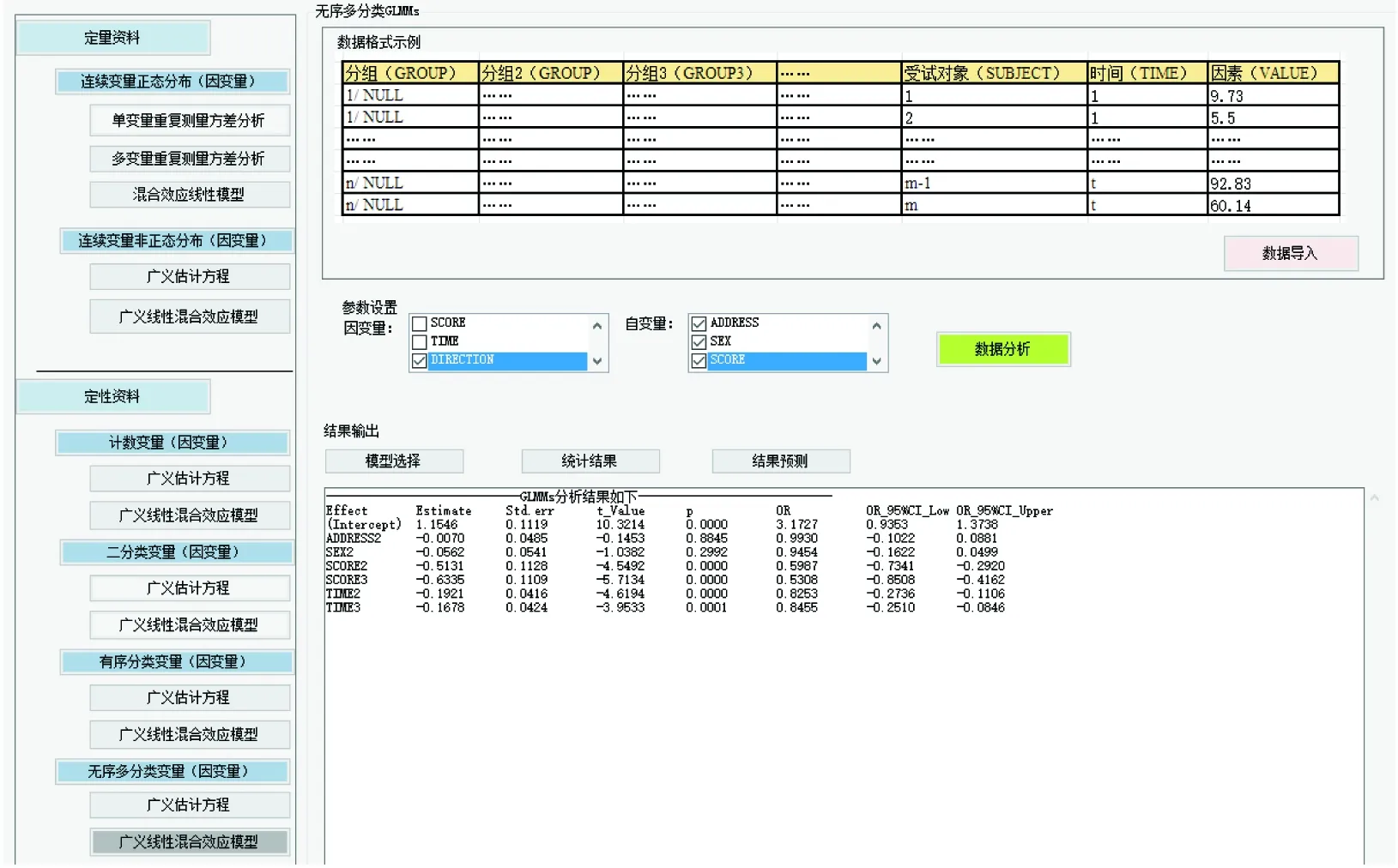
图3 广义估计方程参数估计结果

①从图3可以清晰看到，组间比较结果，单纯西医的疗效显著低于中西医结合，Wald卡方=9.701，B=-1.735<0且P<0.01，更进一步，单纯西医的有效率是中西医结合的exp(-1.735)=17.63%；

②基线数据影响结果：年龄不能显著影响有效率，P值均大于0.05；

③重复测量时间比较结果：治疗后1月的有效率显著高于治疗后1周，Wald卡方=3.894，B=0.818>0且P=0.048<0.05，更进一步，1月的有效率是1周的2.265倍；治疗后3月的有效率显著高于治疗后1周，Wald卡方=8.819，B=1.502>0且P=0.003<0.05，更进一步，3月的有效率是1周的4.490倍。

c.模型预测准确率

更进一步，我们需要继续考察以上模型的准确率。模型预测的准确率为：

2.广义线性混合效应模型

广义线性混合效应模型是广义线性模型和一般线性混合效应模型的扩展，是在广义线性固定效应模型的基础上引入随机效应，在随机效应满足正态分布的前提下，因变量可以是指数家族中的任一分布，指数家族可有许多基本的离散分布(包括二项分布、泊松分布和负二项式正态分布等)和连续分布(正态分布、beta分布和χ2分布等)组成，当随机效应不存在时，广义线性混合效应模型就退化为广义线性模型[6]。广义线性混合效应模型的自变量可以是分类或连续的，可以处理多个随机效应，建模灵活，且同样可以用于非均衡数据，能较好处理含有缺失值的资料。

(1)模型框架：GLMMS利用逆连接函数来构建线性预测值与条件均数关系的基本模型：

Y=μ+ε

μ=g-1(Xβ+Zγ)

式中，Y：n×l维观测向量；μ：观测的期望(均数)向量；g(·)：可微单调连接函数，g-1(·)：g(·)的转置；X和Z分别是固定效应和随机效应的设计矩阵，X：n×p维矩阵，Z：n×r维矩阵；β和γ分别是模型的固定效应和随机效应的参数向量，随机效应γ应满足均数为0，方差矩阵为G的正态分布，γ～N(0，G)，Var(Y)=G；残差ε～N(0，R)，var(ε)=R，R为残差协方差矩阵[7]。

对于有序多分类结局测量，其连接函数为累积logit函数(cumulative logit function)，采用多层累积logistic回归模型来拟合数据，模型可表达为：

Y=μ+ε

γ～N(0，G)var(ε)=R

其中，μ：多项式概率分布期望向量，有n个延伸的观测。假设有4个分类，可以记作：μ=(μ11，μ12，μ13，…，μn1，μn2，μn3)，μij：观测i在分类j的概率。

(2)参数估计：GLMMS估计的最大似然目的是将如下求积似然函数(integrated likelihood function)最大化：

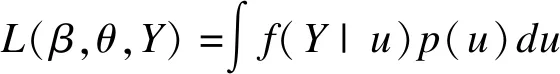
其中β为固定效应，θ为未知的方差/协方差参数，f(Y|u)为随机效应u条件下的结局测量分布函数，p(u)为随机效应的分布函数。此积分似然函数必须近似估计[8]。

(3)背景资料

本研究为一项随访调查研究，观察医学本科毕业生在刚毕业、毕业后3年和毕业后6年的去向选择。研究因素为生源地、性别、学习成绩和毕业时间，因变量为去向选择。

表2 研究中变量说明

(4)R语言程序代码

library(readxl)

data<- read_excel(file.choose())

data$TIME<-factor(data$TIME)

data$ID<-factor(data$ID)

data$SEX<-factor(data$SEX)

data$SCORE<-factor(data$SCORE)

data$ADDRESS<-factor(data$ADDRESS)

library(lme4)

glmms1<- glmer(DIRECTION～ SEX + SCORE + ADDRESS + TIME +(1|ID)，

data=data，family=‘Gamma’)

glmms2<- glmer(DIRECTION～ SEX + SCORE + ADDRESS + TIME +(1|ID)，

data=data，family=‘inverse.gaussian’)

sapply(list(glmms1，glmms2)，AIC)

sapply(list(glmms1，glmms2)，BIC)

coef(summary(glmms2))

confint.glmer(glmms2)

#结果预测

pred=fitted(glmms2)

pred=ifelse(pred>2.5，3，pred)

pred=ifelse(pred<2.5 & pred>1.5，2，pred)

pred=ifelse(pred<1.5，1，pred)

data$PREDICTEDVALUE=pred

library(vcd)

table(data$PREDICTEDVALUE，data$DIRECTION)

addmargins(table(data$PREDICTEDVALUE，data$DIRECTION))

(5)结果展示与表达

本研究采用广义线性混合效应模型研究本案例的无序多分类重复测量的数据，运算结果如下。

a.模型选择

根据赤池信息准则(Akaike information criterion，AIC)和贝叶斯信息准则(Bayesian information criterion，BIC)选择最优模型，结果表明，正态反高斯先验模型的AIC、BIC值均最小，选择正态反高斯先验模型为最优模型。

b.模型拟合结果

图4 广义线性混合效应模型参数估计结果

从图4可以清晰看到：

①基线数据影响结果：性别、生源地不会影响医学生本科毕业后的选择，P值全部大于0.05。

②考试成绩的影响：学习成绩会影响医学生本科毕业后的选择，学习成绩靠后的毕业生选择继续深造而不选择医生和医药公司的可能性明显低于学习成绩靠前的毕业生；学习成绩靠后的毕业生选择继续深造的可能性仅仅只有学习成绩靠前的53.08%(P<0.01)；学习成绩中等的毕业生选择继续深造而不选择医生和医药公司的可能性明显低于学习成绩靠后的毕业生；学习成绩中等的毕业生选择继续深造的可能性仅仅只有学习成绩靠后的59.87%(P<0.01)；基于此，学习成绩好的倾向于继续深造，学习成绩中等的倾向于医生，而成绩较差的倾向于医药公司。

③毕业时间的影响：毕业后3年选择继续深造而不是医生和医药公司的可能性仅仅只有刚毕业的82.53%(P<0.01)，毕业后6年与刚毕业的去向比较更倾向于医生和医药公司(P<0.01)。

c.模型预测准确率

3.结果比较

通过前面R语言程序与SPSS的统计分析结果比较，可以得出两种统计方式结果一致。本软件仅是调用R语言程序包，未做统计方法代码的修改，所以本软件结果即是R语言统计分析结果。因此，本软件的运行结果准确有效。

讨 论

目前，国内有公司推出了在线数据科学分析平台[9](SPSSAU)和易侕软件[10](EmpoertStats)，能够实现自动化统计分析与结果输出功能，同样具有操作简便、结果显示清晰的优点；但不足之处是费用比较高(2588元/年，200元/月等)，且目前无法实现广义估计方程和广义线性混合模型的统计分析。

本研究基于C#语言和R语言开发了一套针对广义估计方程和广义线性混合模型的统计分析软件，该软件具有数据导入、统计分析、模型选择、分析结果和结果预测等功能，实现对临床重复测量定性资料的自动化统计分析。实际使用中，只需选择因变量和自变量就能自动获取统计分析的相关结果，且结果与SPSS软件统计分析结果一致[11-12]。该软件完全免费，安装后医生可以根据收集资料的性质与分析目的，选择适合的统计分析方法和统计图表，只需简单的可视化步骤，便输出统计分析结果与表达，减轻了医生的科研统计压力。不足之处是，前期进行了重复测量设计定量资料的自动化实现，尚未进行重复测量设计生存资料的统计分析，这部分将在以后的研究中进一步探讨。