基于人工鱼群算法的二辊液压轧机辊缝PID控制器优化
2022-09-14罗彩玉刘明
罗彩玉,刘明
(1.阿克苏职业技术学院机电工程学院,新疆 温宿 843100;2.华北理工大学电气工程学院,河北 唐山 063210)
当前,轧机已经成为钢铁制造领域的一个必不可少的设备,轧带产品质量受到辊缝控制效果的显著影响[1-2]。为进一步提高轧带尺寸控制精度,需对辊缝进行精确控制并增强抗干扰能力[3-4]。
樊立萍等[5]综合运用PID方法与模糊逻辑控制方法建立了一种模糊自适应PID控制技术,并对辊缝进行了控制测试,结果显示采用该控制方法表现出了比传统PID方法更优的控制效果。崔佳梅等[6]在测试二辊液压轧机辊缝控制性能的过程中依次对神经网络、PID方法与无模型自适应方法进行了比较分析,结果显示,采用无模型自适应方法能够满足快速收敛的要求,并且大幅减小了稳态误差,使模型获得了更强抗扰动能力。李波等[7]主要对二辊液压轧机辊缝控制运行过程的非线性特性进行了研究,并分析了引起控制参数与输入不稳定性的各项因素,设计得到一种高效的自适应反步滑模控制技术,根据仿真结果可知,自适应反步滑模控制器能够实现高精度跟踪的效果,并且实现了良好的鲁棒性能。王宪等[8]针对二辊液压轧机辊缝控制引起参数波动,以及在外界因素作用下引起轧辊不能达到准确压下位置的过程开展了研究,通过模糊输出反馈的方式来满足同步控制辊缝伺服系统运动过程的要求,根据仿真结果可知,在系统中加入模糊输出反馈条件后除了可以缩短同步时间以外,还能显著降低跟随误差。李建雄等[9]设计了一种利用Anti-Windup抗饱和鲁棒性来实现的动态输出反馈控制算法,将该算法应用到了规格为650 mm的辊缝系统中,结果显示该算法能够满足有效性要求。刘希等[10]将鲁棒H∞控制器应用于二辊液压轧机辊缝控制中,以此实现参数摄动等情况的仿真测试,结果显示该H∞控制器达到了优异跟踪性能并实现了参数摄动的良好鲁棒性。彭珍瑞等[11]为数控机床进给伺服系统构建了一个仿真模型,设计了一种以人工鱼群算法(artificial fish swarm optimization,AFSO)进行优化的PID控制器,并将其跟传统Ziegler-Nichols方法实施了对比分析.通过仿真测试发现,采用人工鱼群PID控制方法获得了比传统形式PID控制方法更优的控制效果,达到了更快的动态响应速率并提升了稳定性。徐秀芬[12]深入分析了对电液比例系统进行PID控制时的参数整定过程,建立一种通过蚁群算法(ant clony optimization,ACO)实现的PID参数优化方案,同时确定了具体控制步骤,结果发现VACA-PID控制器同时获得了优异静、动态性能,充分满足了电液比例系统的调控需求。
综上所述,现阶段关于二辊液压轧机辊缝控制方面的研究基本都是关于系统阶跃响应方面的内容,并且工况条件也比较单一,并不能实现对复杂工况下的轧机系统控制要求。针对以上情况,本文对二辊液压轧机辊缝控制进行了研究,并为系统控制过程构建了开环传递函数,同时运用ACO与AFSO优化了PID控制器的各项参数,最后利用Simulink对比了优化处理后的系统响应速率与抗干扰性。
1 二辊液压轧机辊缝控制方案
1.1 二辊液压轧机辊缝控制原理
轧机工作辊的执行机构控制如图1所示,有2个液压缸,能实现对工作辊垂向运动过程的控制功能。液压缸位移通过测厚仪将信号传输至计算机,其运动过程通过调节伺服阀阀芯位置来实现,由此获得精确的辊缝[13]。对辊缝进行控制的结构原理如图2所示。
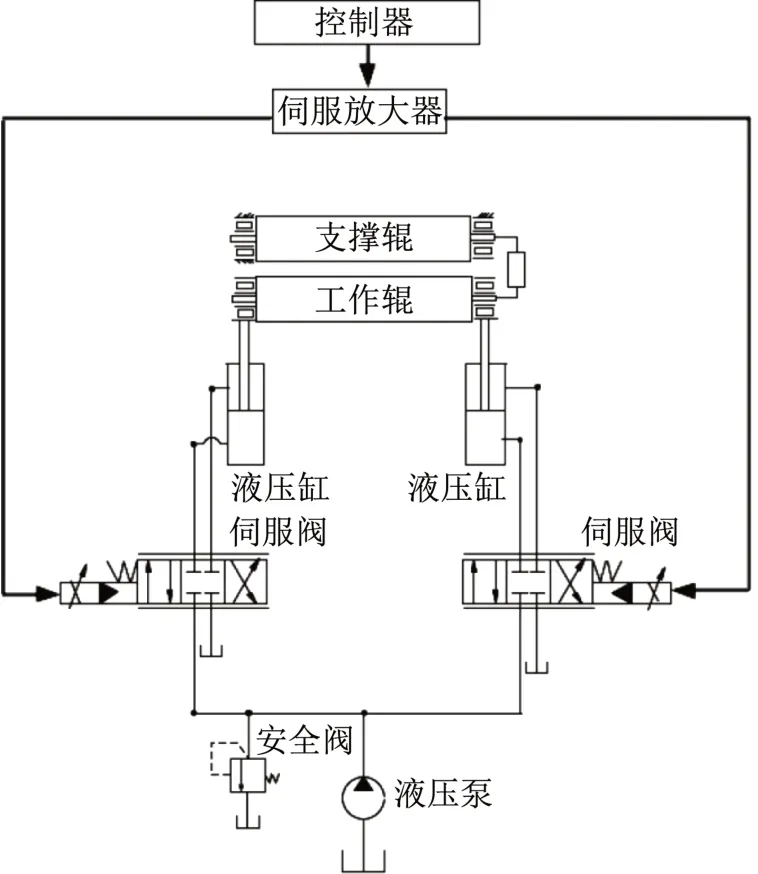
图1 二辊液压轧机辊缝控制原理Fig.1 Roll gap of two high hydraulic mill control schematic diagram
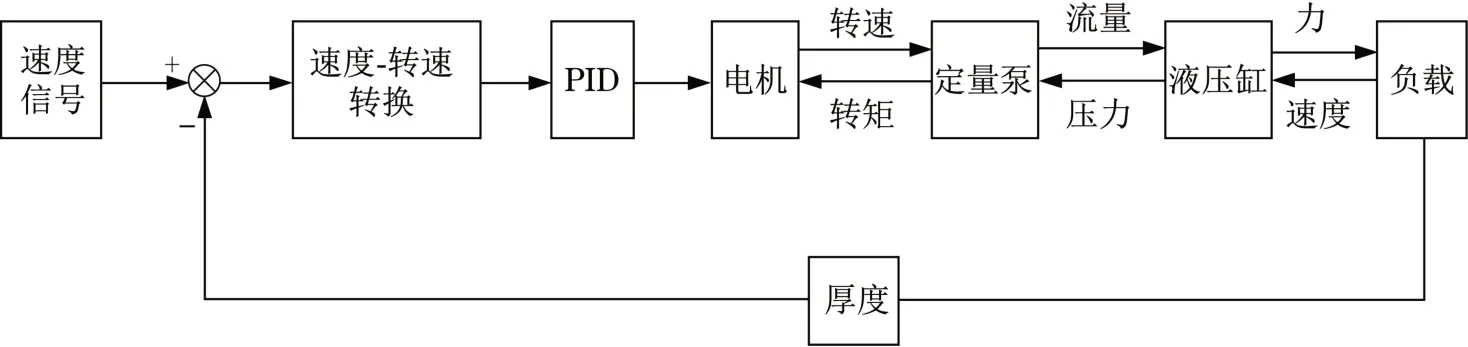
图2 二辊液压轧机辊缝控制方案Fig.2 Roll gap of two high hydraulic mill control scheme
按照以下条件设置系统各项参数:选择原液压缸作为本系统液压缸,半径为39 mm;流量系数介于0.60~0.62之间,本实验采用0.62。主要参数具体见表1。
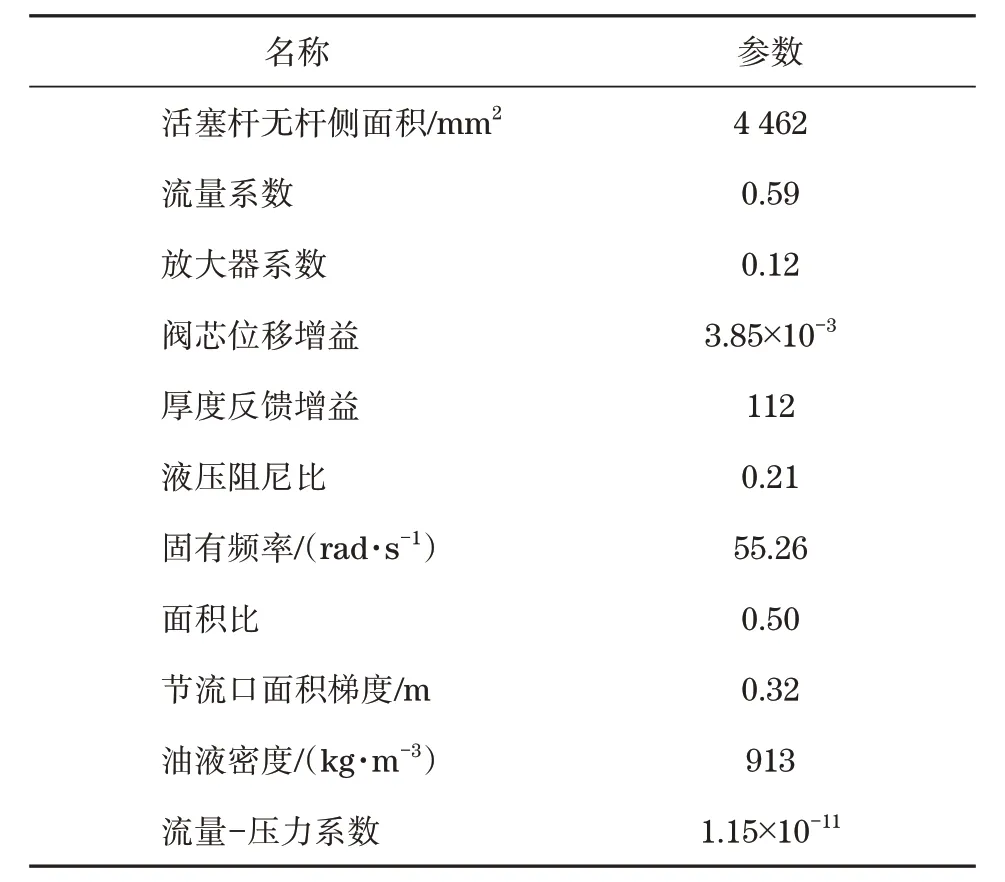
表1 系统主要参数Tab.1 Main system parameters
1.5 控制器设计
通过模仿蚂蚁行为建立ACO,不同蚂蚁间根据各自释放的外激素物质来实现信息传输过程,当蚂蚁沿运动路径产生的信息素不断积累后,便可以实现蚁群集体行为的正反馈效果[14]。采用ACO优化PID的具体框图如图3所示,优化参数取值见表2。
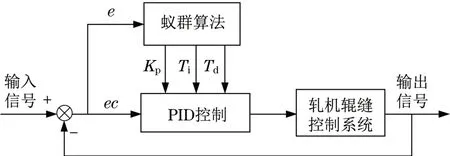
图3 ACO优化PID结构Fig.3 Block diagram of ACO optimized PID parameters

表2 ACO优化参数Tab.2 ACO optimization parameters
利用AFSO对PID的各参数进行了优化。AFSO则是针对鱼群容易聚集到营养丰富的区域进行模仿得到的一种最优解计算方法。AFSO可以实现全局快速收敛的功能,与ACO相比能够有效避免发生局部最优的情况[15]。采用AFSO对PID参数进行优化的具体过程如图4所示。
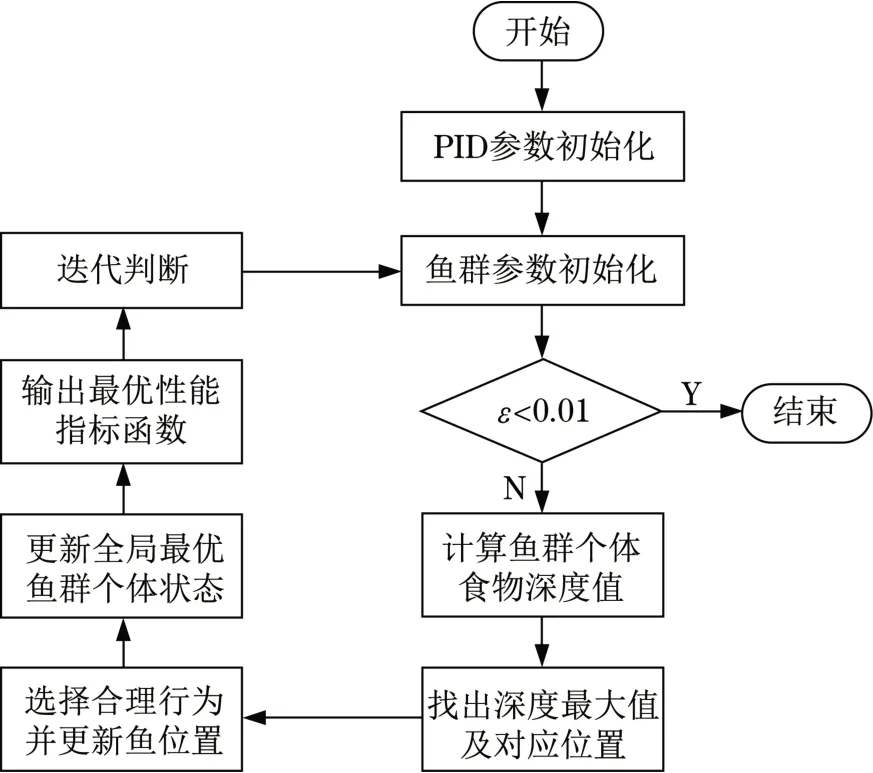
图4 AFSO优化PID流程Fig.4 AFSO optimization PID process
2 仿真分析
根据二辊液压轧机辊缝控制传递函数,利用Simulink构建如图5所示的仿真模型。本研究在系统中加入了阶跃信号与特定频率的随机信号,之后对2种算法进行系统响应与抗干扰性优化的效果进行了分析。
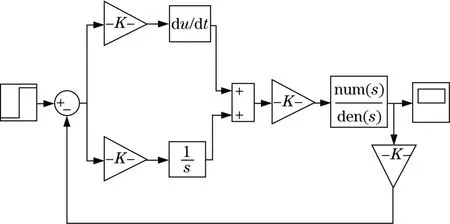
图5 仿真模型Fig.5 Simulation model
2.1 阶跃信号分析
首先将优化后的PID参数加入模型中,再对系统设置阶跃信号,通过仿真获得分别以2种算法进行优化后的系统阶跃响应状态。通过超调量、稳态误差、调整时间来评价阶跃信号的响应性能,未施加干扰力下阶跃响应结果见表3。由表3可见,AFSO获得了比ACO更低的超调量,降低幅度达到13.61%,同时缩短了21.00%的调整时间,并且稳态误差也减小近30.00%,以上结果表明,采用AFSO可以达到比ACO更优的响应性能。
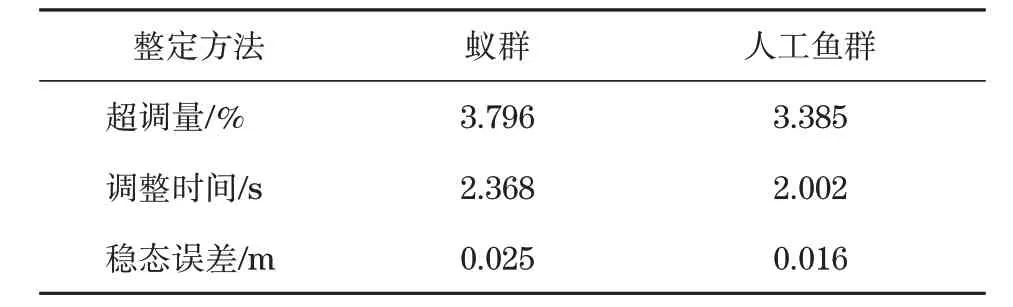
表3 未施加干扰力下阶跃响应结果Tab.3 Step response results without interfering force applied
同时在系统中加入阶跃信号与干扰力信号,对比了2种算法优化后的系统抗干扰效果。对2种算法优化后的系统受到干扰力作用情况下产生的响应差异性结果见表4。经对比发现,受到干扰力作用后,采用AFSO优化的系统,响应曲线超调量下降了12.58%,调整时间缩短了14.58%,稳态误差降低了25.00%。
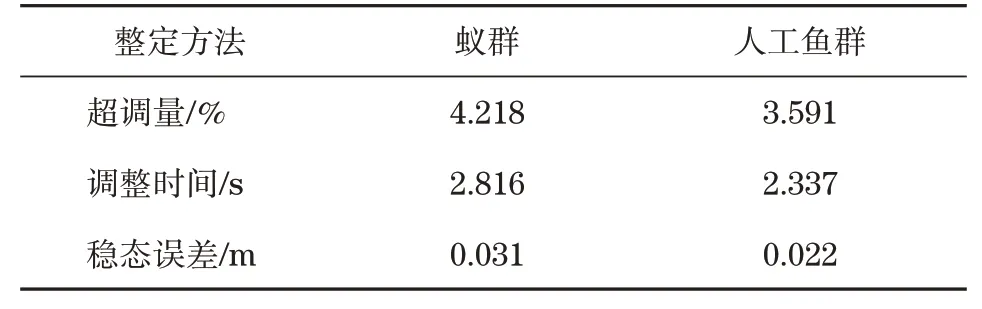
表4 未施加干扰力下阶跃响应结果Tab.4 Step response results with interfering force applied
2.2 随机信号分析
选择Random Number模块在系统中加入不同频率的随机信号。通过仿真获得如图6所示的系统响应曲线。
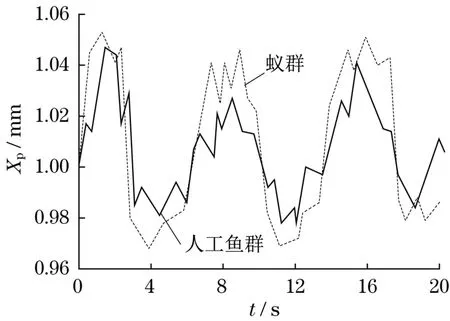
图6 随机信号下系统响应结果Fig.6 System response results under random signal
响应波动范围算法对比结果见表5,给出了对各频率随机信号下形成的系统响应波动情况。由表5可知,逐渐提高随机信号频率后,2种算法获得的响应曲线都发生了波动性降低的变化趋势;在所有频率条件下,AFSO都比ACO表现出了更低的随机信号响应曲线波动范围,表明AFSO具备比ACO更优的响应控制效果。
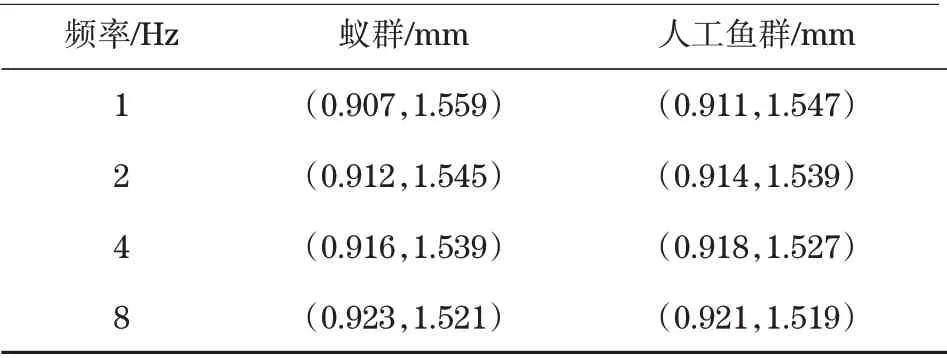
表5 响应波动范围结果统计Tab.5 Statistics of response fluctuation range results
3 结论
(1)阶跃信号未施加干扰力下,AFSO获得了比ACO更低的超调量,降低幅度达到13.61%,同时缩短了21.00%的调整时间,并且稳态误差也减小近30.00%,表明采用AFSO可以达到比ACO更优的响应性能。
(2)阶跃信号施加干扰力下,采用AFSO优化的系统,响应曲线超调量下降了12.58%,调整时间缩短了14.58%,稳态误差降低了25.00%。
(3)逐渐提高随机信号频率后,AFSO都比ACO表现出了更低的随机信号响应曲线波动范围,表明AFSO具备比ACO更优的响应控制效果。
