滑坡堰塞湖溃决风险与过程研究进展

钟启明,陈小康,梅胜尧,单熠博,杜镇瀚

(1. 南京水利科学研究院,江苏 南京 210029；2. 水利部水库大坝安全重点实验室,江苏 南京 210029；3. 河海大学土木与交通学院,江苏 南京 210098)

受地震、降水和融雪等因素影响,山区易发生因崩塌、滑坡、泥石流等堵塞河流形成堰塞湖的地质灾害,其中堵塞河流的堆积物被称为堰塞体[1]。统计全球1 393座堰塞湖案例发现[2],其中50.5%的堰塞湖由地震诱发,39.3%由降水诱发,两者之和接近90%；其他诱因依次为融雪、人为原因和火山喷发。滑坡堰塞湖是其中最常见的一种,也是本文的关注对象。堰塞体作为滑坡堰塞湖的挡水结构,由土石材料组成,但与人工修筑的土石坝存在明显区别,其几何形态、结构与材料特征、水动力条件更为复杂,导致其寿命较之土石坝也更为短暂。主要表现在：①几何形态。堰塞体一般沿河流运动方向堆积长度较大,顶部不平,且上、下游坡比(垂直/水平)较小；土石坝一般形状较为规整,上、下游坡比通常在1∶1.5～1∶3之间[3]。②结构与材料特征。大多数堰塞体结构复杂,材料非均匀性强,颗粒粒径分布范围广泛；土石坝可分为均质坝、心墙坝和面板坝,结构与材料按照相应设计规范人为控制。③水动力条件。由于堰塞体上没有泄洪设施,河流堰塞后易导致堰塞湖水位不断抬升而发生漫顶溃决；土石坝一般设置溢洪道、泄洪洞等泄流设施控制库水位的抬升。统计全球245座已溃堰塞体案例发现[3],漫顶溃决案例占94%,渗透破坏溃决案例占5%,边坡失稳溃决案例仅占1%；统计全球3 504座已溃土石坝案例发现[3],漫顶溃决案例占48%,渗透破坏溃决案例占35%,边坡失稳溃决案例占4%,综合因素导致溃决的案例占13%。④存在时间。统计全球352座已溃堰塞体案例发现[2],84.4%的堰塞体寿命不到1 a,68.2%的堰塞体寿命不到1个月,29.8%的堰塞体寿命不到1 d；土石坝的平均寿命远高于堰塞体[4]。

随着极端气候和地质灾害事件频发,滑坡堰塞湖的溃决过程模拟与风险评估逐渐成为学术界关注的焦点,其中蕴含的关键科学问题包括外荷载作用下滑坡堰塞体的力学响应、滑坡堰塞湖渐进破坏机理与溃决洪水预测理论。自20世纪80年代以来,国内外学者针对堰塞湖的形成、孕灾、致灾机制和应急响应开展了一系列的理论研究和工程实践,研究重点主要包括：堰塞湖形成机制、分类、形态结构特征[1,5],堰塞体粒径分布特征、稳定性及影响因素[5- 8],堰塞湖寿命分析、溃决原因、破坏机制和灾害防控技术[1,3,9- 10]等。滑坡堰塞湖的溃决过程模拟与风险评估研究中存在材料随机性、结构空间变异性、荷载不确定性和非恒定流冲蚀特性等难题,涉及多学科交叉、多场耦合、多尺度模拟,目前对此领域研究进展的综述还不够翔实。本文针对滑坡堰塞湖溃决风险与过程研究中的关键科学问题,从堰塞湖危险性评价、堰塞体溃决机理试验、堰塞湖溃决洪水预测等3个方面综述国内外的相关研究进展和存在的问题,并对未来的研究方向提出建议。

1 堰塞湖危险性评价

滑坡堰塞湖导致的灾害能否级联放大取决于堰塞湖是否会发生溃决,这也是堰塞湖危险性评价的关键点。一般而言,堰塞湖的危险性与堰塞体的形态特征和物质组成、堰塞湖水动力条件以及当地的次生灾害相关。围绕这些影响因素,国内外学者开展了一系列的研究,总体来说可分为定性和定量2种评价方法。

1.1 定性评价方法

堰塞湖危险性定性评价主要是从堰塞湖的形成机理和地貌学特征、堰塞体材料物理力学特性等方面来开展。定性评价方法可分为工程类比法和历史分析法[11]。工程类比法是将待评价堰塞湖的形成机理和地质条件与同类已溃或未溃堰塞湖进行比较,以确定其危险性；历史分析法是根据堰塞湖的形成历史和演变过程对其危险性进行评价。定性评价方法具有无需进行数学计算的特点,评价指标可通过遥感[12]或地球物理方法[13]获取。近年来,遥感技术在分辨率、准确性、采集速度等方面都取得了长足进步,已成为堰塞湖识别与调查的有力工具,可用于堰塞湖的几何形态描述和堰塞体的变形监测；对于没有数据的地区,可采用无人机进行光学摄影测量。地球物理方法可用于堰塞体物质组成的测量,常用的方法包括3类[8],即电磁勘探、地电勘探和地震勘探。

总体来说,目前将获取的信息单纯用于定性评价的研究较少,大多作为定量评价的基础数据。准确、快速地获取堰塞湖地貌学指标和堰塞体材料物理力学特性是进行堰塞湖危险性评价和溃决洪水分析的基础。

1.2 定量评价方法

定量评价方法作为堰塞湖危险性评价的主流方法,根据计算方法的特点可分为数理统计法、物理模型试验法和数值分析法。

1.2.1 数理统计法

根据全球范围内已溃和未溃堰塞湖案例,学者们基于多元回归的数理统计方法,建立了一系列数学表达式和判断准则,对堰塞湖的危险性进行快速评价。1999年,Casagli等[14]基于70座北亚平宁地区的堰塞湖案例,以堰塞体体积和堰塞湖汇水面积作为输入参数,提出了以堆积体指标(BI)判断堰塞湖危险性的方法,根据计算结果,堰塞湖可分为安全、危险和不确定3种状态。随后,Ermini等[15]、Korup[5]、Stefanelli等[16]也分别根据不同的案例提出了一系列基于地貌学指标的堰塞湖危险性快速评价方法。为了消除堰塞湖危险性评价中的不确定性,学者们又提出了基于逻辑回归的数理统计方法,定义计算结果大于0的堰塞湖是安全的,并给出了堰塞湖的溃决概率计算方法[3]。基于43座日本堰塞湖案例,Dong等[17]分别提出了3类指标用于堰塞湖危险性的评价,输入参数主要包括入流量、堰塞体的长/宽/高/体积、堰塞湖汇水面积等。随后,石振明等[18]分别提出了3参数和5参数表达式来评价堰塞湖的危险性。为了考虑堰塞体的物质组成,Shan等[19]也分别提出了精细化和简化表达式对堰塞湖的危险性进行评判,并考虑了堰塞湖的地貌学指标(如堰塞体的宽/高/体积、堰塞湖汇水面积)，其中精细化表达式可考虑堰塞体的级配特征,简化表达式可定性考虑堰塞体的物质组成。另外,中国的水利行业标准《堰塞湖风险等级划分与应急处置技术规范：SL/T 450—2021》[20]根据堰塞湖库容、上游来水量、堰塞体物质组成和堰塞体形态等指标,并依据定量分级指标将堰塞湖的危险性分为4个级别,分别为极高危险、高危险、中危险和低危险。目前国内外典型的堰塞湖危险性评估模型可查阅文献[14- 20]。

就目前的研究现状而言,回归分析是最常用的数理统计方法,但取决于样本的可靠性以及判别指标的合理性和代表性。随着堰塞湖资料的不断丰富,运用数理统计方法进行评价的准确性也有望逐渐提高。另外,随着智能算法的发展,基于大数据的机器学习方法为堰塞湖危险性的评价提供了一种新的途径。

1.2.2 物理模型试验法

堰塞湖危险性评价物理模型试验主要以小尺度简化模型试验为主。近年来,国内学者基于不同的致灾因子,开展了考虑地震荷载的振动台试验和考虑涌浪作用的水槽模型试验[21- 22]。总的来说,物理模型试验法通过堰塞湖的基础资料,采用相似的物理材料制成模型来还原堰塞体的可能破坏,是评价堰塞湖危险性的一种直观方法。但该方法一般将堰塞体作为形状规则、材料较为均匀的坝体处理,与真实的堰塞体有所差异,再加上模型缩尺和边界条件简化等问题,一般用于机理的揭示。

1.2.3 数值分析法

堰塞体的上、下游坡比通常较小,在自重作用下一般不会发生边坡失稳。目前,关于堰塞湖危险性评价的数值分析方法主要集中在不同外部荷载作用下(如非稳定渗流、余震、降水等[23- 25])堰塞体的稳定性分析,模拟时一般考虑堰塞体形态和内部结构、材料的物理力学特性,以及堰塞湖的水动力条件。常用的数值分析方法有极限平衡法、有限元法、有限差分法和离散元法。由于存在堰塞体结构、材料、外荷载及荷载组合等不确定性问题,数值分析中模型构建和计算参数选取难度较大,往往无法合理反映实际情况,且绝大多数堰塞湖寿命较短,因此堰塞湖危险性评价中较少采用数值分析方法,大多数此类研究都是堰塞湖溃决后进行的反馈分析。

2 堰塞湖溃决机理试验

堰塞湖的溃决过程涉及复杂的水土耦合效应,而堰塞湖多位于交通闭塞的山谷中,溃决历时短、洪水流量大,现场数据采集困难,国内外目前关于堰塞湖溃决过程的记录相对较少。为了更好地揭示堰塞湖的溃决机理及其影响因素,学者们开展了大量的物理模型试验。

2.1 堰塞湖溃决过程与溃决机理

堰塞湖溃决过程表现为非恒定水流对堰塞体的非线性冲蚀,一般而言,模型试验可分为小尺度(高度<1 m)、大尺度(高度≥1 m)[26]和离心(超重力场)模型试验。

对于小尺度模型试验,Yang等[27]通过7组高度为0.3 m的模型试验,将溃决过程分为渗流侵蚀—初始溃口形成—溯源冲蚀—溃口扩展—河道再平衡5个阶段；Zhou等[28]通过4组高度为0.7 m的模型试验,将溃决过程分为陡坎侵蚀—加速冲蚀—衰减冲蚀3个阶段；Zhu等[29]通过12组高度为0.3 m的模型试验,将溃决过程分为起始—陡坎侵蚀—加速冲蚀—河床再平衡4个阶段。对于大尺度模型试验,Li等[30]通过3组高度为2.5 m的模型试验,将溃决过程分为初始—发展—破坏3个阶段；Zhang等[31]也基于此3组试验将溃决过程分为溯源冲蚀—快速冲蚀—衰减冲蚀3个阶段；Takayama等[32]通过2组高度为1.0 m的模型试验,将溃决过程分为渐进冲蚀—漫顶冲蚀2个阶段；Zhou等[33]通过2组高度为2.0 m的现场模型,分别模拟了漫顶破坏和漫顶- 渗流耦合破坏2种模式,并将溃决过程分为初始—溃口流量快速增加—溃口流量衰减3个阶段。对于离心模型试验,Zhao等[34]通过2组原型高度为6.0 m(模型高度0.2 m,离心加速度30 g)的模型试验,将溃决过程分为下游坡冲蚀—冲槽下切—冲槽侧壁淘刷—溃口边坡失稳—下游坝坡粗化5个阶段。另外,基于“11·03”白格堰塞湖溃决过程的实测数据,Zhong等[35]将溃决过程分为均匀冲蚀—溯源冲蚀—沿程侵蚀—溃口稳定4个阶段。

虽然学者们将堰塞湖的溃决过程划分为不同的发展阶段,但从溃口流量和形态的突变来看,堰塞湖的溃决过程均表现为起始阶段—加速阶段—稳定阶段。其中,下游坡初始冲坑形成和溯源冲蚀发生在起始阶段(图1(a),图1(b))；溯源冲蚀发展至上游堰塞湖后发生沿程侵蚀,溃决过程进入加速阶段(图1(c))；当入流和出流达到平衡时,溃决过程进入稳定阶段,此后溃口的发展基本停止(图1(d))。

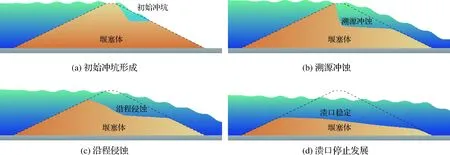
图1 堰塞体溃决过程示意Fig.1 Schematic diagram for landslide dam breach process

基于目前的研究成果,堰塞湖的溃决机理可总结如下：堰塞体发生漫顶溢流后,初始漫顶水流流速较低,加之堰塞体具有宽级配的特征,漫顶水流对堰塞体顶部未造成明显冲蚀,受重力作用影响,初始冲坑首先出现在下游坡；随后,漫顶水头对初始冲坑进行淘刷,并发生溯源冲蚀直至堰塞体上游坡顶部；随着溯源冲蚀发展至堰塞湖,漫顶水头突然增大,初始溃口形成,溃决过程进入加速阶段,增大的漫顶水头增强了水流的冲蚀能力,溃口在纵、横向都得到了快速发展,直至出现峰值流量；随着水位的下降和溃口过流能力的增加,溃口冲蚀逐渐减弱直至进入稳定阶段,当入流量等于溃口出流量时,溃决过程结束,溃口流量最终降至河流的基流量。另外,通过大量的模型试验和现场观测发现,堰塞体在纵断面(顺河向)方向下游坡角呈逐渐变缓的趋势，在横断面(横河向)方向的溃口呈倒梯形状,在水流冲蚀作用下发生连续性纵向下切和横向扩展,并伴随溃口边坡的间歇性失稳坍塌。

2.2 堰塞湖溃决过程影响因素分析

为了深入研究堰塞湖的溃决机理,国内外学者开展了一系列考虑不同影响因素的模型试验。影响因素可分为5类：堰塞体形态(如下游坡角、高度等[36- 37]),堰塞体材料物理力学指标(如级配、初始含水率、渗透系数、密实度等[38- 41]),堰塞湖水动力条件(如河道比降、入流量等[39，42]),泄流槽(如是否开挖、断面型式、位置等[30，42- 43]),外荷载(如涌浪[44]等)。通过模型试验发现：

(1) 下游坡角与冲蚀率、溃口流量并不是简单的递增关系,而是存在一定的阈值,但对于阈值的范围还没有明确的认识；堰塞体高度越大,相应的堰塞湖体积越大,水动力条件越强,溃口峰值流量越大,而峰值流量出现时间提前与否取决于溃口的扩展速度。

(2) 当堰塞体材料级配良好时,其抗冲蚀能力较强,溃口峰值流量相对较小且出现时间较晚,溃决历时相对较长,溃决过程相对平稳；随着初始含水率的增加,溃口峰值流量增加,溃决历时和堰塞体残留高度减小,但现有的研究成果并不一致,且缺乏高初始含水率条件下的模型试验；对于渗透系数较小的堰塞体,在蓄水阶段堰塞体内无法形成稳定渗流场,漫顶溃决起主导作用；对于渗透系数较大的堰塞体,可能会在漫顶溢流之前发生下游边坡失稳或渗透破坏；随着堰塞体密实度的增加,溃口峰值流量减小,溃口峰值流量出现时间也会滞后。

(3) 随着河道比降的增大,冲蚀过程加剧,溃口峰值流量出现时间提前；入流量增大时,溃决过程加快,冲蚀速率增大。

(4) 如果不开挖泄流槽,溃口峰值流量会增加；在相同开挖量的条件下,复合型泄流槽能有效地提高泄流效率,并使溃口流量过程相对平缓；当泄流槽靠近岸坡时,发生单侧冲蚀,最终溃口宽度较小,残留堰塞体体积较大。

(5) 在遭受涌浪时,堰塞体的稳定性由有效水位与堰塞体高度之差决定,材料的冲蚀率由浪高和平均粒径决定。

近年来的堰塞湖溃决模型试验虽然考虑了各类影响因素,但仍存在如下问题值得深入研究：① 堰塞体一般由宽级配土石材料构成,而模型试验的最大粒径一般小于2 cm,少量试验达到4 cm,材料冲蚀特征的相似关系需进一步明确；② 由于堰塞体形成原因、滑坡体的物质组成和运动模式均存在显著差异,导致堰塞体内部结构的多样性,而传统的模型试验大多采用均匀拌合材料的方式制模,没有考虑堰塞体的内部结构差异。

3 堰塞湖溃决洪水预测

堰塞湖溃决洪水预测是堰塞湖溃决风险与过程研究的核心和关键,由于堰塞体复杂的物质组成和结构特征,对于其溃决时溃口峰值流量及洪水流量过程的科学预测是溃决洪水演进合理性的重要保证。20世纪80年代以来,为了对堰塞湖的溃决洪水进行预测,国内外学者基于已溃堰塞湖的调查资料、物理模型试验和理论分析,提出了一系列的数学模型。总体来说,数学模型可分为3类,即经验模型、基于溃决机理的简化模型和基于溃决机理的精细化模型[26]。

3.1 堰塞湖溃决过程经验公式与数值模拟

3.1.1 经验模型

经验模型一般基于已溃堰塞湖案例的实测数据,采用回归分析等方法提出预测溃决参数的经验公式。溃口峰值流量作为堰塞湖溃决洪水严重性的关键考量指标最受关注。Costa[45]基于10座堰塞湖溃决案例,最早提出了3个预测堰塞湖溃口峰值流量的回归方程,输入参数分别为堰塞体高度、堰塞湖容积或两者组合。此后,Costa等[1]、Evans[46]、Walder等[47]分别基于不同的堰塞湖溃决案例,建立了溃口峰值流量的表达式。总的来说,早期的经验模型仅考虑了堰塞湖的地貌学指标或溃决时的水动力条件,数学表达式也多为单参数或双参数；随后,石振明等[48]分别基于24座和26座堰塞湖溃决案例,提出了考虑地貌学指标的5参数和3参数模型。近年来,堰塞体的材料特性对溃口峰值流量的影响越发引起学者们的重视。Peng等[49]基于45座堰塞湖溃决案例,考虑堰塞湖的地貌学指标和堰塞体材料的冲蚀特性(分为高、中、低),提出了预测堰塞湖溃口峰值流量的表达式；Ruan等[50]基于67座堰塞湖溃决案例,提出了考虑材料冲蚀特性、溃口形状、堰塞体形态和堰塞湖容积的溃口峰值流量表达式。基于Fan等[51]提出的考虑颗粒分布特征的堰塞体3种分类(间接对应高、中、低的冲蚀特性),Froehlich[52]根据42座堰塞湖溃决案例,提出了考虑堰塞湖地貌学指标和堰塞体分类的溃口峰值流量表达式。Shan等[53]基于86座堰塞体的颗粒级配特征,定义了基于颗粒组成的冲蚀因子,并结合44座已溃堰塞湖的地貌学指标提出了溃口峰值流量的表达式。国内外用于预测堰塞湖溃口峰值流量的典型经验模型可参阅文献[1,45,47- 53]。

由于堰塞体材料的宽级配特征,堰塞湖在溃决后往往存在残留堰塞体,因此,在经验模型中充分考虑堰塞体的材料特性对于溃口峰值流量的预测至关重要。近年来,随着堰塞湖溃决案例基础数据的不断丰富,以反映堰塞湖地貌学指标(如堰塞湖容积,堰塞体长、宽、高、体积,汇水面积等)和堰塞体物质组成(或冲蚀特性)为特点的新一代堰塞湖溃决峰值流量经验模型的预测精度较单纯考虑地貌学指标的模型明显提升。虽然经验模型可快速获取堰塞湖的溃口峰值流量,但此类模型无法提供溃口洪水流量过程和峰值流量出现时间,常用于堰塞湖溃决风险的快速评估和初步评判。

3.1.2 基于溃决机理的简化模型

随着堰塞湖溃决过程数值模拟重视程度的逐渐提高,基于溃决机理的简化模型得到了快速发展。模型通常假设堰塞体形状规整,初始溃口为规则形态(如倒三角形、矩形或倒梯形),在溃决过程中溃口尺寸发生变化,部分模型可考虑溃决过程中溃口边坡的失稳,分别采用宽顶堰流量公式和冲蚀方程模拟溃口水流和材料冲蚀。现场调查表明,堰塞体颗粒分布在深度方向上存在分层现象,不同滑坡形式的堰塞体颗粒分布也存在差异[3]。如何合理地反映堰塞体的结构特征、宽级配材料的冲蚀特性,以及横断面和纵断面溃口形态的演化过程是堰塞湖溃决过程模拟的关键。

基于剪应力的冲蚀率公式已被广泛应用于溃口底床下切过程的模拟。冲蚀率可表示为冲蚀系数乘以水流剪应力和材料临界剪应力之差。其中,水流剪应力可通过曼宁公式计算,冲蚀系数与材料临界剪应力可通过试验测定。当参数无法通过试验获取时,对于冲蚀系数,Chang等[54]基于堰塞体现场实测资料拟合得出了宽级配材料的冲蚀公式；对于材料临界剪应力,Annandale[55]提出了针对宽级配材料的计算公式。此外,Chen等[56]提出了一种描述土体冲蚀速率的双曲线模型,并基于现场测量回归预测了最大可能的冲蚀率。

对于横断面方向的溃口发展,通常假设侧向冲蚀率等于溃口底床冲蚀率或乘以一个系数；边坡失稳坍塌是溃口横向扩展的主要机制,常采用平面或圆弧滑动面的极限平衡法。对于纵断面方向的溃口发展,各模型的主要不同之处在于对溃决过程中下游坡角变化的假设；目前常用的有3种假设,例如,下游坡角保持不变或减小或增加到某个值后保持不变。另外,为了考虑堰塞体的结构特性,一些模型考虑了沿深度方向材料冲蚀特性或颗粒分布特征的变化。

目前,国外较为常用的可用来模拟堰塞湖溃决的数学模型主要包括NWS BREACH模型[57]、BEED模型[58]和DLBreach模型[59]。国内有3种典型的堰塞湖溃决过程简化模型也被广泛应用,包括香港科技大学DABA模型[60]、中国水利水电科学研究院的DB- IWHR模型[56]以及南京水利科学研究院的DB- NHRI模型[61],这些模型已应用于易贡、唐家山、白格、加拉等典型堰塞湖溃决过程的反馈分析和预测,取得了良好的效果。

简化模型一般采用按时间步长迭代的计算方法输出各时间步长的溃决参数,该类模型的优点在于计算效率高,且在一定程度上反映堰塞湖的溃决机理。但模型在堰塞体形状、溃口形态、材料物理力学特性、溃口流量和溃口边坡稳定性分析方面引入了大量假设。此外,由于采用不同的公式分别计算溃口流量和溃口发展,此类模型不能真正反映堰塞湖溃决过程中的水土耦合效应。

3.1.3 基于溃决机理的精细化模型

基于Naiver- Stokes(N- S)方程和各类泥沙冲蚀模型,并通过一定的简化和假设处理,学者们建立了一系列描述土石材料坝溃决的1- D、2- D和3- D精细化数学模型。模型通常包含3个模块,即水动力模块(清水或浑水的质量守恒和动量守恒方程)、坝料冲蚀模块(平衡或非平衡输沙方程)、溃口形态演化模块(溃口底部和侧向发展方程)。根据溃坝模型中冲蚀方程的不同,精细化模型大体可分为4类[62- 66]：平衡模型、非平衡模型、两相流模型及两层流模型。另外,也有学者耦合不同类型的模型,提出了双层平均两相流模型[67]。平衡模型主要由N- S方程(1- D、2- D和3- D)和Exner方程组成,N- S方程(纯水)描述水流运动,Exner方程描述溃口形态的演化过程,此类模型还经常采用各种经验公式计算冲蚀率。非平衡模型一般假定溃口水流为水沙混合物,采用N- S方程(浑水)来描述水流过程,假设坝料运动形式由推移质和悬移质2部分组成,常根据经验公式确定推移质和悬移质的运移及相互转化过程；此类模型将实际冲蚀率换算成浑水体积浓度,由浑水体积浓度和流速计算冲蚀过程。两相流模型假设溃口挟沙水流中固体颗粒的体积浓度较低,坝体颗粒在水流的驱动力下运动,但固液两相之间的相互作用较弱；在连续介质假设的基础上,建立固液两相运动的连续性方程和动量守恒方程,其中固相具有类似于颗粒流的特性。两层流模型假定溃口底床上方的水流由上部清水层和下部推移质层组成,每一层都有各自的深度和浓度；清水层与推移质层之间存在清水交换,推移质层与溃口底床之间存在坝料交换,交换量通常由经验公式确定,在此基础上分别建立清水层和挟沙层的连续性方程和动量守恒方程。

为了求解上述4类模型的控制方程,可采用欧拉法或拉格朗日法。对于欧拉法,常基于计算流体力学(CFD)的方法,采用有限差分法、有限元法或有限体积法等有网格计算方法进行离散求解[68]。与欧拉法不同,拉格朗日法具有模拟流体界面发生较大拓扑变化的优势,在溃坝过程模拟中,常用一种无网格计算方法——光滑粒子流体动力学(SPH)方法[69]。另外,有一种方法兼具欧拉法和拉格朗日法的特点——物质点法(MPM),MPM使用固定的欧拉网格计算作用力,同时也存储拉格朗日粒子的信息,并且保证两者之间的信息传输[70]。

上述方法主要基于连续介质力学,近年来,学者们引入离散元方法(DEM),基于连续- 非连续介质力学耦合的方法模拟溃坝过程,主要包括CFD- DEM法[71]和SPH- DEM法[72]等。耦合方法的优点是通过不连续颗粒模拟坝料,可再现溃坝水流作用下颗粒的运动,并计算获取溃口流量过程线。CFD- DEM法和SPH- DEM法虽然能更清晰地反映水土耦合作用下的溃坝机理,但颗粒数量和形状、坝体尺寸、时间步长等指标的设置受时空尺度的限制明显,由于计算成本过高,此类耦合方法目前在实际溃坝案例的模拟中应用较少。

此4类精细化模型都可以在各自的假设和理论框架下模拟溃坝过程中的溃口洪水流量过程和溃口形态演化过程,但在实际应用中仍存在一些困难。如何选择合适的冲蚀公式是关键问题之一,大多数冲蚀公式是在均匀流、输沙强度小、溃口底床变形缓慢的条件下得到的,这些理论缺陷限制了精细化模型的仿真能力,亟需开发能够合理反映宽级配堰塞体材料在高速水流作用下的冲蚀特性和堰塞湖溃决机理的模型。此外,虽然精细化模型可以有效提高数值模拟的精度,但在模拟大尺度堰塞湖溃决过程时的计算效率仍然较低。随着计算机处理能力的增强,GPU加速技术被引入到一些模型中[73],提高了溃决水流的计算效率。总体而言,基于溃决机理的精细化模型是堰塞湖溃决过程数值模拟的发展方向。

3.2 溃决洪水演进数值模拟

溃决洪水演进是灾害损失评估的重要步骤,常采用经验公式法和数值分析法进行研究。经验公式法一般基于溃口峰值流量或最大流速,考虑洪水演进区域的下垫面特点(如山区、丘陵或平原地区)、断面距坝址距离等因素,直接计算下游某处的洪水峰值流量、流速、洪水到达时间等参数[74]。数值分析法一般将溃决过程模拟中获取的溃口洪水流量过程线作为边界条件,采用数值模拟手段对洪水淹没范围、水深、流速及洪水到达时间等各要素进行评估。

对于数值分析方法,按照计算的维度,溃决洪水演进可分为1- D、2- D和3- D模型,另外1- D和2- D耦合模型也是研究中常用的方法。溃决洪水演进模拟时的控制方程通常也是不同形式的N- S方程,溃决水流与一般的河道水流相比,具有更高的水流流速和非线性。1- D计算时,通常使用激波拟合法和激波捕获法[75]；1- D溃决洪水演进的计算效率高,但忽略了横向扩散对洪水的影响。因此，许多学者致力于2- D、3- D溃决洪水波的数值计算,限于问题本身的复杂性和目前对机理的认识程度,计算时采用了简化处理的方法[76]。目前也有一些商业软件被广泛应用于溃坝洪水演进,如FLDWAV、DHI MIKE FLOOD、HEC- RAS等[77- 79]。

对于经验模型和基于溃决机理的简化模型,开展洪水演进模拟时常将溃口洪水流量过程线作为边界条件输入,因此将溃决洪水模拟人为分割为溃口流量模拟和洪水演进模拟2部分；由于作为边界条件输入时通常不考虑溃决洪水的流速,导致计算获取的下游淹没区洪水到达时间存在一定的误差。对于精细化模型,由于溃口流量与洪水演进模拟的控制方程一致,可将下游淹没区统一建模,避免了分别计算带来的误差,且可以考虑溃口挟沙水流在下游演进过程中的沉积特征和对河道地形的重塑作用。

4 结论与建议

本文针对滑坡堰塞湖溃决风险与过程研究这一主题,总结了堰塞湖危险性评价、堰塞体溃决机理试验、堰塞湖溃决洪水预测等3个方面的研究进展。总体而言,经过近40a的系统研究,学者们已经对滑坡堰塞湖溃决风险与过程有了一定的认识,并初步构建了堰塞湖风险评估的基本框架,但目前国内外关于本领域的研究还处于起步阶段,仍存在一些值得深入探讨的问题：

(1) 堰塞湖危险性评价中的不确定性问题。由于形成条件、物质组成等存在不确定性,采用传统的确定性方法无法考虑堰塞体颗粒分布的空间变异性和宽级配特征等问题。建议采用“空”(高分辨光学影像与InSAR)、“天”(机载LiDAR与无人机航拍)、“地”(地表与内部观测)一体化监测技术获取堰塞湖的地貌学与堰塞体物质组成参数；基于外荷载(水位持续抬升、滑坡涌浪、地震作用等)时空分布规律,研究堰塞湖可能承受的极端荷载及其组合,研究堰塞体的力学响应规律,提出堰塞体破坏模式判别方法；基于概率统计和机器学习算法,系统研究堰塞体材料物理力学参数空间变异特性和极端荷载发生的概率分布特性,建立相应的概率表征方法；基于堰塞湖危险性各影响因素(堰塞体形态和物质组成、堰塞湖水动力条件)因果关系构建贝叶斯网络拓扑结构,研究不同荷载或荷载组合对堰塞湖整体危险性的影响,提出堰塞湖破坏概率计算方法。

(2) 宽级配材料冲蚀特性与堰塞湖溃决过程物理模拟方法。由于滑坡堰塞体在堆积过程中存在颗粒分选机制,采用不同级配土体均匀拌合的模型试验无法合理反映挟沙水流作用下溃口的演化规律和坝体残留特征。建议通过开发相关仪器,测试土水界面水流剪应力以及土体冲蚀率,确定堰塞体材料的临界启动剪应力,研究应力状态、含水率、水流速度、水流挟沙浓度等因素对宽级配材料冲蚀率的影响,揭示堰塞体材料在非恒定流作用下的动态冲蚀特性；通过模型试验研究堰塞湖溃决过程中堰塞体的溯源冲蚀和沿程侵蚀速率、流量变化过程、溃口边坡坍塌范围,确定溃决过程不同阶段转变的时刻和条件,揭示堰塞湖的渐进破坏机理与影响因素。

(3) 考虑水土耦合的堰塞湖溃决洪水高效仿真方法。由于堰塞体颗粒组成呈现宽级配特征,采用传统河道泥沙冲蚀方程无法考虑材料的特性；堰塞湖溃决过程与洪水演进通常分别计算,缺乏统一考虑水土耦合机制的堰塞湖溃决全过程洪水预测模拟方法。建议摒弃采用平均粒径表征颗粒级配导致模拟误差的方法,按颗粒分布特征对粒径进行分组,采用多个粒径描述堰塞体材料的宽级配特性,建立非恒定水流作用下的材料冲蚀方程；基于堰塞体溃口演化规律,构建溃口底床高程演化方程与溃口边坡失稳判别方法,综合考虑堰塞湖、堰塞体和下游河道地貌学特征,建立考虑水土耦合的堰塞湖溃决洪水数学模型,实现堰塞湖溃决过程与洪水演进中挟沙水流运动特征的一体化模拟。